جافا فرز الفقاعة

إذا كنت قد سمعت من قبل عن طرق الفرز في البرمجة، فمن المرجح أن تكون خوارزمية فرز الفقاعات. إنها واحدة مشهورة. يعرف كل مبرمج خوارزمية الفرز الفقاعي (أو على الأقل سمع عنها أثناء التعلم) ليس لأنها أفضل خوارزمية فرز في العالم، بل لأنها الأسهل. تُستخدم هذه الخوارزمية عادةً لأغراض التعلم أو قد تحصل عليها كمهمة في مقابلة Java Junior الخاصة بك. من السهل جدًا فهم خوارزمية فرز Java Bubble، إلا أنها ليست فعالة. على أي حال، دعونا معرفة ذلك.

ما هو الفرز

بادئ ذي بدء، عليك أن تفهم ما هو الفرز بشكل عام وما يمكننا فرزه في برامج Java. إذا تمكنا من مقارنة عنصرين أو كائنات أو أكثر بأي من سماتها، فهذا يعني أنه يمكن فرزها حسب هذه السمة. على سبيل المثال، الأرقام بترتيب تصاعدي أو تنازلي أو الكلمات أبجديًا. ومن ثم، يجب أن تكون العناصر قابلة للمقارنة مع بعضها البعض. بالمناسبة عناصر ماذا؟ في Java، يمكننا مقارنة عناصر المجموعات. على سبيل المثال يمكننا فرز Array أو ArrayList للأعداد الصحيحة والسلاسل وما إلى ذلك.

كيف يعمل فرز الفقاعة

لنفترض أننا بحاجة إلى فرز مجموعة من الأعداد الصحيحة بترتيب تصاعدي، أي من الأصغر إلى الأكبر. أولاً، نحن نسير على طول المصفوفة بأكملها ونقارن كل عنصرين متجاورين. إذا كانوا بالترتيب الخاطئ (الجار الأيسر أكبر من الجار الأيمن)، فإننا نتبادلهم. في التمريرة الأولى في النهاية سيظهر العنصر الأكبر (إذا قمنا بالفرز بترتيب تصاعدي). يمكنك القول أن العنصر الأكبر هو "الملوثات العضوية الثابتة". هذا هو سبب اسم خوارزمية فرز الفقاعات. نكرر الخطوة الأولى من العنصر الأول إلى العنصر الذي يليه. لدينا ثاني أكبر عنصر في المكان قبل الأخير. وما إلى ذلك وهلم جرا. يمكننا تحسين الخوارزمية قليلاً من خلال التحقق مما إذا كان قد تم إجراء تبادل واحد على الأقل في الخطوة السابقة. إذا لم يكن الأمر كذلك، فسنتوقف عن الركض على طول المصفوفة.

مثال لفرز الفقاعة

لنقم بفرز مجموعة الأعداد الصحيحة، العدد الذي قد تراه أدناه في الصورة. الخطوة 1: نمر عبر المصفوفة. تبدأ الخوارزمية بالعنصرين الأولين (مع المؤشرات 0 و1)، و8 و7، وتتحقق مما إذا كانت بالترتيب الصحيح. من الواضح أن 8 > 7، لذلك قمنا بتبديلهما. بعد ذلك، ننظر إلى العنصرين الثاني والثالث (المؤشران 1 و 2)، والآن هما 8 و 1. ولنفس الأسباب، نقوم بتبديلهما. للمرة الثالثة نقارن 8 و 2، وعلى الأقل 8 و 5. لقد قمنا بأربعة تبادلات في المجموع: (8، 7)، (8، 1)، (8، 2) و (8، 5). ظهرت القيمة 8، وهي الأكبر في هذه المصفوفة، في نهاية القائمة في الموضع الصحيح. 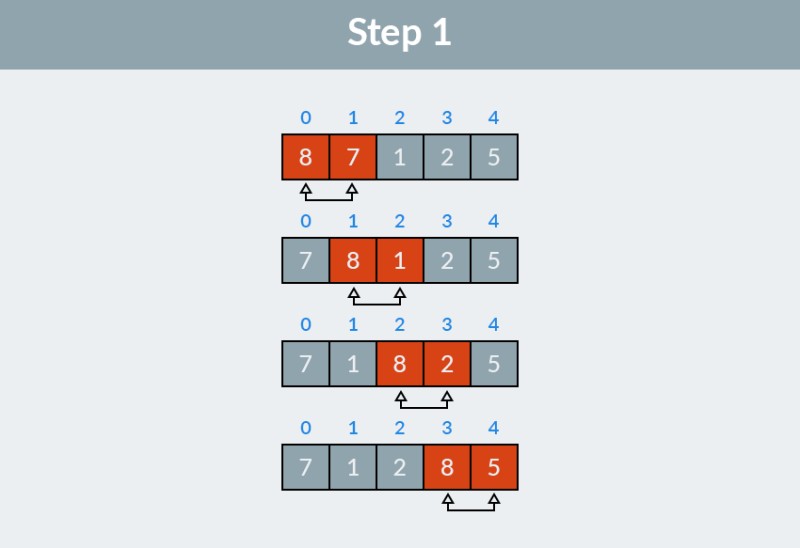نتيجة الخطوة الأولى من عمل خوارزمية فرز الفقاعات هي المصفوفة التالية: الخطوة 2. افعل الشيء نفسه مع (7,1) و(7,2) و(7,5). 7 الآن في الموضع قبل الأخير، ولا نحتاج إلى مقارنته بـ "ذيل" القائمة، فقد تم فرزه بالفعل. نتيجة الخطوة الثانية من عمل خوارزمية فرز الفقاعات هي المصفوفة التالية: كما ترى، تم فرز هذه المصفوفة بالفعل. على أية حال، يجب أن تبدأ خوارزمية فرز الفقاعات مرة أخرى على الأقل. الخطوه 3. نحن نمر عبر المصفوفة مرة أخرى. لا يوجد شيء يمكن تبديله هنا، لذلك إذا كنا نستخدم خوارزمية فرز الفقاعات "المحسنة" (مع التحقق مما إذا كان قد تم إجراء تبادل واحد على الأقل في الخطوة السابقة) فإن هذه الخطوة هي الخطوة الأخيرة.

كود جافا لفرز الفقاعات

تحقيق نوع فقاعة جافا

لنقم بإنشاء طريقتين لفرز الفقاعات. الأول، bubbleSort(int[] myArray) هو مستوى واحد. يتم تشغيله من خلال المصفوفة في كل مرة. الثاني، الأمثلBubbleSort(int myArray[]) تم تحسينه عن طريق إيقاف الخوارزمية إذا لم تتسبب الحلقة الداخلية في أي مبادلة. يوضح لك العداد عدد الخطوات التي قمت بها أثناء الفرز. هنا لدينا تنفيذ Java من نوع Bubble:

import java.util.Arrays;

public class BubbleSortExample {

   //  Plane Bubble sort example

   public static int[] bubbleSort(int[] myArray) {

       int temp = 0;  //  temporary element for swapping
       int counter = 0;  //  element to count quantity of steps

       for (int i = 0; i < myArray.length; i++) {
           counter = i + 1;
           for (int j = 1; j < (myArray.length - i); j++) {

               if (myArray[j - 1] > myArray[j]) {
                   //  swap array’s elements using temporary element
                   temp = myArray[j - 1];
                   myArray[j - 1] = myArray[j];
                   myArray[j] = temp;
               }
           }
       }
       System.out.println("Steps quantity, non optimized = " + counter);
       return myArray;
   }
   //  An optimized version of Java Bubble Sorting

   static int[] optimizedBubbleSort(int myArray[]) {
       int temp;
       boolean swapped;
       int counter = 0;  //  element to count quantity of steps
       for (int i = 0; i < myArray.length - 1; i++) {
           counter = i + 1;
           swapped = false;
           for (int j = 0; j < myArray.length - i - 1; j++) {
               //  counter++;
               if (myArray[j] > myArray[j + 1]) {
                   //  swap arr[j] and arr[j+1]
                   temp = myArray[j];
                   myArray[j] = myArray[j + 1];
                   myArray[j + 1] = temp;
                   swapped = true;

               }
           }  //  counter = i;
           //  If there weren't elements to swap in inner loop, then break
           if (swapped == false) {

               break;

           }
       }
       System.out.println("steps quantity, optimized = " + counter);
       return myArray;
   }


   public static void main(String[] args) {
       int arr[] = {8, 7, 1, 2, 5};
       int arr1[] = {8, 7, 1, 2, 5};

       System.out.println("Array arr Before Bubble Sort");
       //  we use java.util.Arrays toString method to print the array
 System.out.println(Arrays.toString(arr));

       System.out.println("Array arr After Bubble Sort");
       System.out.println(Arrays.toString(bubbleSort(arr)));

       System.out.println("Array arr1 Before Bubble Sort");
       System.out.println(Arrays.toString(arr1));

       System.out.println("Array arr1 After Optimized Bubble Sort");
       System.out.println(Arrays.toString(optimizedBubbleSort(arr1)));
   }
}

نتيجة عمل خوارزمية جافا لفرز الفقاعات:

Array arr Before Bubble Sort
[8, 7, 1, 2, 5]
Array arr After Bubble Sort
Steps quantity, non optimized = 5
[1, 2, 5, 7, 8]
Array arr1 Before Bubble Sort
[8, 7, 1, 2, 5]
Array arr1 After Optimized Bubble Sort
steps quantity, optimized = 3
[1, 2, 5, 7, 8]

ما مدى كفاءة فرز الفقاعات؟

يعد فرز الفقاعات أحد أسهل الخوارزميات التي يمكن تنفيذها ولكنها ليست فعالة. يتطلب زوجًا من الحلقات المتداخلة. حتى في النسخة المحسنة من الخوارزمية، في أسوأ الحالات (كل عنصر في مجموعة البيانات يكون في ترتيب عكسي للعنصر المطلوب)، تتكرر الحلقة الخارجية مرة واحدة لكل عنصر من العناصر n في مجموعة البيانات. تتكرر الحلقة الداخلية n مرات the للمرة الأولى، ( n-1 ) للمرة الثانية، وهكذا. وبالتالي، لترتيب جميع عناصر n ، يجب تنفيذ الحلقات n*(n-1)/2 مرات. إنه يستدعي التعقيد الزمني O(n ² ) ويعني أن الخوارزمية تقوم بحوالي 500000 مقارنة لـ 1000 عنصر من المصفوفة. ومع ذلك، فإن خوارزمية الفرز الفقاعي فعالة جدًا في استخدام الذاكرة (تعقيد الذاكرة هو O(n) ) وهي جيدة حقًا لمجموعات البيانات الصغيرة التي تم فرزها تقريبًا.