التعقيد الخوارزمي

أهلاً! سيكون درس اليوم مختلفًا قليلاً عن البقية. وسوف يختلف من حيث أنه يرتبط بشكل غير مباشر فقط بجافا. ومع ذلك، هذا الموضوع مهم جدًا لكل مبرمج. سنتحدث عن الخوارزميات . ما هي الخوارزمية؟ بعبارات بسيطة، إنها سلسلة من الإجراءات التي يجب إكمالها لتحقيق النتيجة المرجوة . نحن نستخدم الخوارزميات في كثير من الأحيان في الحياة اليومية. على سبيل المثال، كل صباح لديك مهمة محددة: الذهاب إلى المدرسة أو العمل، وفي نفس الوقت تكون:

• الملبس
• ينظف
• تغذيها

ما هي الخوارزمية التي تتيح لك تحقيق هذه النتيجة؟

1. الاستيقاظ باستخدام المنبه.
2. استحم واغسل نفسك.
3. قم بإعداد وجبة الإفطار وبعض القهوة أو الشاي.
4. يأكل.
5. إذا لم تقم بكي ملابسك في الليلة السابقة، قم بكويها.
6. يرتدى ملابسة.
7. اترك المنزل.

سيسمح لك تسلسل الإجراءات هذا بالتأكيد بالحصول على النتيجة المرجوة. في البرمجة، نحن نعمل باستمرار لإنجاز المهام. يمكن تنفيذ جزء كبير من هذه المهام باستخدام خوارزميات معروفة بالفعل. على سبيل المثال، لنفترض أن مهمتك تتمثل في ما يلي: فرز قائمة تضم 100 اسم في مصفوفة . هذه المهمة بسيطة للغاية، ولكن يمكن حلها بطرق مختلفة. إليك أحد الحلول الممكنة: خوارزمية فرز الأسماء أبجديًا:

1. قم بشراء أو تنزيل طبعة 1961 من قاموس ويبستر الدولي الجديد الثالث.
2. ابحث عن كل اسم من قائمتنا في هذا القاموس.
3. اكتب على قطعة من الورق صفحة القاموس التي يوجد عليها الاسم.
4. استخدم قطع الورق لفرز الأسماء.

هل سيحقق هذا التسلسل من الإجراءات مهمتنا؟ نعم، بالتأكيد سوف. هل هذا الحل فعال ؟ بالكاد. نأتي هنا إلى جانب آخر مهم جدًا من الخوارزميات: كفاءتها . هناك عدة طرق لإنجاز هذه المهمة. لكن سواء في البرمجة أو في الحياة العادية، نريد اختيار الطريقة الأكثر كفاءة. إذا كانت مهمتك هي صنع قطعة من الخبز المحمص بالزبدة، فيمكنك البدء بزراعة القمح وحلب البقرة. لكن هذا سيكون حلاً غير فعال ، فهو سيستغرق الكثير من الوقت وسيكلف الكثير من المال. يمكنك إنجاز مهمتك البسيطة بمجرد شراء الخبز والزبدة. على الرغم من أنها تسمح لك بحل المشكلة، إلا أن الخوارزمية التي تتضمن القمح والبقرة معقدة للغاية بحيث لا يمكن استخدامها عمليًا. في البرمجة، لدينا تدوين خاص يسمى تدوين O الكبير لتقييم مدى تعقيد الخوارزميات. يتيح Big O تقييم مدى اعتماد وقت تنفيذ الخوارزمية على حجم بيانات الإدخال . دعونا نلقي نظرة على أبسط مثال: نقل البيانات. تخيل أنك بحاجة إلى إرسال بعض المعلومات في شكل ملف لمسافة طويلة (على سبيل المثال، 5000 ميل). ما هي الخوارزمية التي ستكون أكثر كفاءة؟ ذلك يعتمد على البيانات التي تعمل معها. على سبيل المثال، لنفترض أن لدينا ملفًا صوتيًا يبلغ حجمه 10 ميغابايت. في هذه الحالة، الخوارزمية الأكثر فعالية هي إرسال الملف عبر الإنترنت. لا يمكن أن يستغرق الأمر أكثر من دقيقتين! دعونا نعيد صياغة الخوارزمية الخاصة بنا: "إذا كنت تريد نقل المعلومات في شكل ملفات عبر مسافة 5000 ميل، فيجب عليك إرسال البيانات عبر الإنترنت". ممتاز. الآن دعونا نحللها. فهل ينجز مهمتنا؟ حسنًا، نعم، إنه كذلك. ولكن ماذا يمكننا أن نقول عن تعقيدها؟ حسنًا، الآن أصبحت الأمور أكثر إثارة للاهتمام. الحقيقة هي أن الخوارزمية الخاصة بنا تعتمد بشكل كبير على البيانات المدخلة، أي حجم الملفات. إذا كان لدينا 10 ميغا، فكل شيء على ما يرام. ولكن ماذا لو كنا بحاجة إلى إرسال 500 ميغابايت؟ 20 جيجا؟ 500 تيرابايت؟ 30 بيتابايت؟ هل ستتوقف خوارزميتنا عن العمل؟ لا، كل هذه الكميات من البيانات يمكن بالفعل نقلها. وسوف يستغرق وقتا أطول؟ نعم! الآن نحن نعرف ميزة مهمة في الخوارزمية الخاصة بنا: كلما زادت كمية البيانات التي سيتم إرسالها، كلما استغرق تشغيل الخوارزمية وقتًا أطول . لكننا نرغب في الحصول على فهم أكثر دقة لهذه العلاقة (بين حجم البيانات المدخلة والوقت اللازم لإرسالها). في حالتنا، التعقيد الخوارزمي خطي. "الخطي" يعني أنه مع زيادة كمية البيانات المدخلة، فإن الوقت المستغرق لإرسالها سيزيد بشكل متناسب تقريبًا. إذا تضاعفت كمية البيانات، فإن الوقت اللازم لإرسالها سيكون ضعف ذلك. إذا زادت البيانات بمقدار 10 مرات، فسيزيد وقت الإرسال 10 مرات. باستخدام تدوين O الكبير، يتم التعبير عن تعقيد الخوارزمية لدينا كـ O(n) . يجب أن تتذكر هذا الترميز للمستقبل، فهو يُستخدم دائمًا للخوارزميات ذات التعقيد الخطي. لاحظ أننا لا نتحدث عن عدة أشياء قد تختلف هنا: سرعة الإنترنت، والقوة الحسابية لجهاز الكمبيوتر الخاص بنا، وما إلى ذلك. عند تقييم مدى تعقيد الخوارزمية، فإنه ببساطة ليس من المنطقي أن نأخذ هذه العوامل في الاعتبار - ففي أي حال، فهي خارجة عن سيطرتنا. يعبر تدوين Big O عن مدى تعقيد الخوارزمية نفسها، وليس "البيئة" التي تعمل فيها. فلنواصل مثالنا. لنفترض أننا تعلمنا في النهاية أننا بحاجة إلى إرسال ملفات يبلغ إجمالي حجمها 800 تيرابايت. يمكننا بالطبع إنجاز مهمتنا عن طريق إرسالها عبر الإنترنت. هناك مشكلة واحدة فقط: بمعدلات نقل البيانات المنزلية القياسية (100 ميجابت في الثانية)، سيستغرق الأمر حوالي 708 يومًا. ما يقرب من 2 سنوات! :O من الواضح أن خوارزميتنا ليست مناسبة هنا. نحن بحاجة إلى حل آخر! بشكل غير متوقع، تأتي شركة أمازون العملاقة لتكنولوجيا المعلومات لإنقاذنا! تتيح لنا خدمة Snowmobile من Amazon تحميل كمية كبيرة من البيانات إلى وحدة تخزين الهاتف المحمول ومن ثم تسليمها إلى العنوان المطلوب بالشاحنة! لذلك، لدينا خوارزمية جديدة! "إذا كنت تريد نقل المعلومات على شكل ملفات على مسافة 5000 ميل، وسيستغرق إرسالها عبر الإنترنت أكثر من 14 يومًا، فيجب عليك إرسال البيانات على شاحنة أمازون." لقد اخترنا 14 يومًا بشكل تعسفي هنا. لنفترض أن هذه هي أطول فترة يمكننا انتظارها. دعونا نحلل الخوارزمية لدينا. وماذا عن سرعته؟ حتى لو كانت الشاحنة تسير بسرعة 50 ميلاً في الساعة فقط، فإنها ستقطع 5000 ميل في 100 ساعة فقط. هذا ما يزيد قليلاً عن أربعة أيام! وهذا أفضل بكثير من خيار إرسال البيانات عبر الإنترنت. وماذا عن مدى تعقيد هذه الخوارزمية؟ هل هو خطي أيضًا، أي O(n)؟ لا ليست كذلك. ففي نهاية المطاف، لا تهتم الشاحنة بمدى الثقل الذي تحمله بها، فهي ستظل تسير بنفس السرعة تقريبًا وتصل في الوقت المحدد. سواء كان لدينا 800 تيرابايت، أو 10 أضعاف ذلك، ستظل الشاحنة تصل إلى وجهتها في غضون 5 أيام. بمعنى آخر، تتميز خوارزمية نقل البيانات المعتمدة على الشاحنات بتعقيد مستمر . هنا، تعني كلمة "ثابت" أنه لا يعتمد على حجم البيانات المدخلة. ضع محرك أقراص فلاش سعة 1 جيجابايت في الشاحنة، وسيصل خلال 5 أيام. ضع أقراصًا تحتوي على 800 تيرابايت من البيانات، وستصل خلال 5 أيام. عند استخدام تدوين O الكبير، يُشار إلى التعقيد الثابت بواسطة O(1) .و O(1) فلننظر الآن إلى المزيد من الأمثلة في عالم البرمجة :) لنفترض أنه تم إعطاؤك مصفوفة مكونة من 100 رقم، والمهمة هي عرض كل منها على وحدة التحكم. تكتب forحلقة عادية تؤدي هذه المهمة

int[] numbers = new int[100];
// ...fill the array with numbers

for (int i: numbers) {
   System.out.println(i);
}

ما هو مدى تعقيد هذه الخوارزمية؟ خطي، أي O(ن). يعتمد عدد الإجراءات التي يجب على البرنامج تنفيذها على عدد الأرقام التي يتم تمريرها إليه. إذا كان هناك 100 رقم في المصفوفة، فسيكون هناك 100 إجراء (عبارات لعرض السلاسل على الشاشة). إذا كان هناك 10000 رقم في المصفوفة، فيجب تنفيذ 10000 إجراء. هل يمكن تحسين خوارزميتنا بأي شكل من الأشكال؟ لا، بغض النظر عن ذلك، سيتعين علينا جعل N يمر عبر المصفوفة وتنفيذ عبارات N لعرض السلاسل على وحدة التحكم. النظر في مثال آخر.

public static void main(String[] args) {

   LinkedList<Integer> numbers = new LinkedList<>();
   numbers.add(0, 20202);
   numbers.add(0, 123);
   numbers.add(0, 8283);
}

لدينا فراغ LinkedListندخل فيه عدة أرقام. نحتاج إلى تقييم التعقيد الخوارزمي لإدراج رقم واحد في LinkedListمثالنا، وكيف يعتمد ذلك على عدد العناصر في القائمة. الجواب هو O(1)، أي التعقيد المستمر . لماذا؟ لاحظ أننا نقوم بإدخال كل رقم في بداية القائمة. بالإضافة إلى ذلك، ستتذكر أنه عند إدراج رقم في ملف LinkedList، فإن العناصر لا تتحرك في أي مكان. يتم تحديث الروابط (أو المراجع) (إذا نسيت كيفية عمل LinkedList، فاطلع على أحد دروسنا القديمة ). إذا كان الرقم الأول في قائمتنا هو x, وقمنا بإدراج الرقم y في مقدمة القائمة، فكل ما علينا فعله هو ما يلي:

x.previous  = y;
y.previous = null;
y.next = x;

عندما نقوم بتحديث الروابط، لا يهمنا عدد الأرقام الموجودة بالفعلLinkedList ، سواء كانت واحدة أو مليار. تعقيد الخوارزمية ثابت، أي O(1).

التعقيد اللوغاريتمي

لا تُصب بالذعر! :) إذا كانت كلمة "لوغاريتمي" تجعلك ترغب في إغلاق هذا الدرس والتوقف عن القراءة، فما عليك سوى الانتظار لبضع دقائق. لن يكون هناك أي رياضيات مجنونة هنا (هناك الكثير من التفسيرات المشابهة لذلك في مكان آخر)، وسوف نختار كل مثال على حدة. تخيل أن مهمتك هي العثور على رقم محدد واحد في مجموعة مكونة من 100 رقم. بتعبير أدق، تحتاج إلى التحقق مما إذا كان هناك أم لا. بمجرد العثور على الرقم المطلوب، ينتهي البحث، وتعرض ما يلي في وحدة التحكم: "تم العثور على الرقم المطلوب! فهرسه في المصفوفة = ...." كيف يمكنك إنجاز هذه المهمة؟ الحل هنا واضح: تحتاج إلى تكرار عناصر المصفوفة واحدًا تلو الآخر، بدءًا من الأول (أو من الأخير) والتحقق مما إذا كان الرقم الحالي يطابق الرقم الذي تبحث عنه. وبناء على ذلك، فإن عدد الإجراءات يعتمد بشكل مباشر على عدد العناصر الموجودة في المصفوفة. إذا كان لدينا 100 رقم، فمن المحتمل أن نحتاج إلى الانتقال إلى العنصر التالي 100 مرة وإجراء 100 مقارنة. إذا كان هناك 1000 رقم، فمن الممكن أن يكون هناك 1000 مقارنة. من الواضح أن هذا هو التعقيد الخطي، أي O(n) . والآن سنضيف تحسينًا واحدًا إلى مثالنا: المصفوفة التي تحتاج إلى العثور على الرقم فيها مرتبة بترتيب تصاعدي . فهل يغير هذا شيئا فيما يتعلق بمهمتنا؟ لا يزال بإمكاننا إجراء بحث قوي عن الرقم المطلوب. ولكن بدلاً من ذلك، يمكننا استخدام خوارزمية البحث الثنائية المعروفة .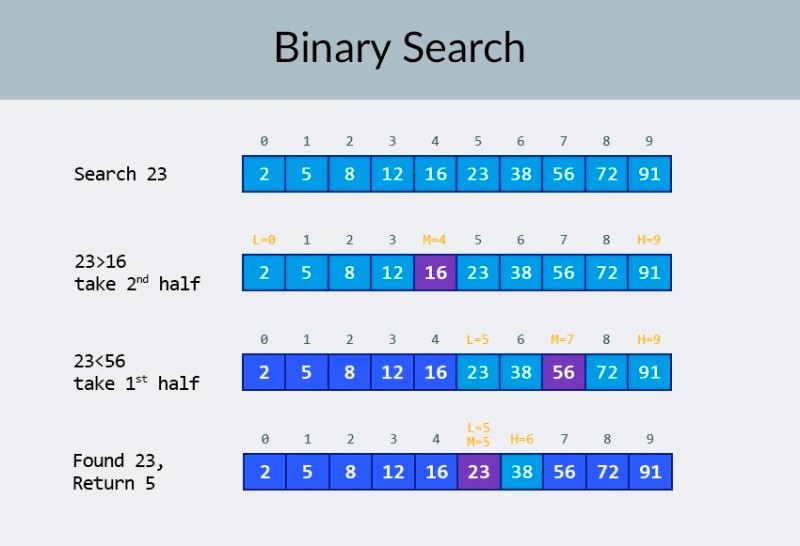 في الصف العلوي من الصورة، نرى مصفوفة مرتبة. علينا العثور على الرقم 23 فيه. بدلاً من التكرار على الأرقام، نقوم ببساطة بتقسيم المصفوفة إلى جزأين والتحقق من الرقم الأوسط في المصفوفة. ابحث عن الرقم الموجود في الخلية 4 وتحقق منه (الصف الثاني في الصورة). هذا الرقم هو 16، ونحن نبحث عن 23. والرقم الحالي أقل مما نبحث عنه. ماذا يعني ذالك؟ هذا يعني أن جميع الأرقام السابقة (تلك الموجودة قبل الرقم 16) لا تحتاج إلى التحقق : فهي مضمونة لتكون أقل من الرقم الذي نبحث عنه، لأن مصفوفتنا مرتبة! نواصل البحث بين العناصر الخمسة المتبقية. ملحوظة:لقد أجرينا مقارنة واحدة فقط، ولكننا قمنا بالفعل بحذف نصف الخيارات الممكنة. لم يتبق لدينا سوى 5 عناصر. سنكرر خطوتنا السابقة بتقسيم المصفوفة الفرعية المتبقية إلى النصف مرة أخرى وأخذ العنصر الأوسط مرة أخرى (الصف الثالث في الصورة). الرقم هو 56، وهو أكبر من الذي نبحث عنه. ماذا يعني ذالك؟ هذا يعني أننا حذفنا 3 احتمالات أخرى: الرقم 56 نفسه وكذلك الرقمين اللذين بعده (حيث أنه من المؤكد أنهما أكبر من 23، لأن المصفوفة مرتبة). لم يتبق لدينا سوى رقمين للتحقق منهما (الصف الأخير في الصورة) - الأرقام ذات مؤشري المصفوفة 5 و6. نتحقق من أولهما، ونجد ما كنا نبحث عنه - الرقم 23! مؤشره هو 5! دعونا نلقي نظرة على نتائج الخوارزمية لدينا، وبعد ذلك سنقوم بتحليل مدى تعقيدها. بالمناسبة، أنت الآن تفهم سبب تسمية هذا بالبحث الثنائي: فهو يعتمد على تقسيم البيانات إلى النصف بشكل متكرر. والنتيجة مثيرة للإعجاب! إذا استخدمنا البحث الخطي للبحث عن الرقم، سنحتاج إلى ما يصل إلى 10 مقارنات، ولكن مع البحث الثنائي أنجزنا المهمة بـ 3 فقط! في أسوأ الحالات، سيكون هناك 4 مقارنات (إذا كان الرقم الذي أردناه في الخطوة الأخيرة هو الثاني من الاحتمالات المتبقية، وليس الأول. فماذا عن تعقيده؟ هذه نقطة مثيرة للاهتمام للغاية :) البحث الثنائي الخوارزمية أقل اعتمادًا على عدد العناصر في المصفوفة من خوارزمية البحث الخطي (أي التكرار البسيط). مع وجود 10 عناصر في المصفوفة، سيحتاج البحث الخطي إلى 10 مقارنات كحد أقصى، لكن البحث الثنائي سيحتاج إلى 4 مقارنات كحد أقصى. وهذا فرق بعامل 2.5. لكن بالنسبة لمصفوفة مكونة من 1000 عنصر ، سيحتاج البحث الخطي إلى ما يصل إلى 1000 مقارنة، لكن البحث الثنائي سيتطلب 10 مقارنة فقط ! الفرق الآن 100 ضعف! ملحوظة:زاد عدد العناصر في المصفوفة 100 مرة (من 10 إلى 1000)، لكن عدد المقارنات المطلوبة للبحث الثنائي زاد بعامل 2.5 فقط (من 4 إلى 10). إذا وصلنا إلى 10000 عنصر ، فسيكون الفرق أكثر إثارة للإعجاب: 10000 مقارنة للبحث الخطي، وإجمالي 14 مقارنة للبحث الثنائي. ومرة أخرى، إذا زاد عدد العناصر بمقدار 1000 مرة (من 10 إلى 10000)، فإن عدد المقارنات يزيد بعامل 3.5 فقط (من 4 إلى 14). تعقيد خوارزمية البحث الثنائي هو لوغاريتمي ، أو، إذا استخدمنا تدوين O الكبير، O(log n) . لماذا هو يسمى ذلك؟ اللوغاريتم هو مثل عكس الأسي. اللوغاريتم الثنائي هو القوة التي يجب رفع الرقم 2 إليها للحصول على رقم. على سبيل المثال، لدينا 10000 عنصر نحتاج إلى البحث عنها باستخدام خوارزمية البحث الثنائي. 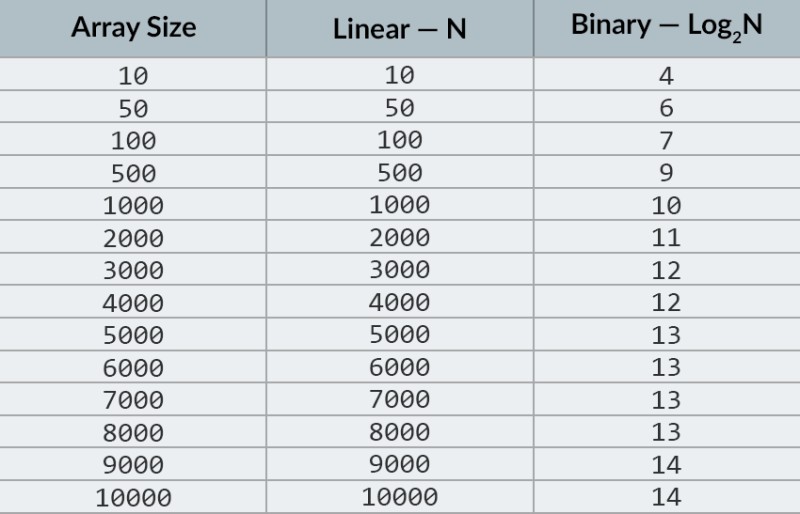حاليًا، يمكنك إلقاء نظرة على جدول القيم لتعرف أن القيام بذلك سيتطلب 14 مقارنة كحد أقصى. ولكن ماذا لو لم يقدم أحد مثل هذا الجدول وتحتاج إلى حساب الحد الأقصى لعدد المقارنات بالضبط؟ كل ما تحتاجه هو الإجابة على سؤال بسيط: ما القوة التي تحتاجها لرفع الرقم 2 بحيث تكون النتيجة أكبر من أو تساوي عدد العناصر المراد التحقق منها؟ بالنسبة لـ 10000، فهي القوة الرابعة عشرة. 2 أس 13 صغير جدًا (8192)، لكن 2 أس 14 = 16384 ، وهذا الرقم يحقق شرطنا (أكبر من أو يساوي عدد العناصر في المصفوفة). لقد وجدنا اللوغاريتم: 14. هذا هو عدد المقارنات التي قد نحتاجها! :) تعد الخوارزميات والتعقيد الخوارزمي موضوعًا واسعًا جدًا بحيث لا يتناسب مع درس واحد. لكن معرفة ذلك أمر مهم للغاية: فالعديد من مقابلات العمل ستتضمن أسئلة تتضمن الخوارزميات. من الناحية النظرية، يمكنني أن أوصي لك ببعض الكتب. يمكنك البدء بـ " خوارزميات Grokking ". الأمثلة في هذا الكتاب مكتوبة بلغة بايثون، لكن الكتاب يستخدم لغة وأمثلة بسيطة جدًا. إنه الخيار الأفضل للمبتدئين، والأكثر من ذلك، أنه ليس كبيرًا جدًا. ومن بين القراءة الأكثر جدية، لدينا كتب لروبرت لافور وروبرت سيدجويك . كلاهما مكتوب بلغة Java، مما سيجعل التعلم أسهل قليلاً بالنسبة لك. بعد كل شيء، أنت على دراية تامة بهذه اللغة! :) بالنسبة للطلاب الذين يتمتعون بمهارات جيدة في الرياضيات، فإن الخيار الأفضل هو كتاب توماس كورمين . لكن النظرية وحدها لن تملأ بطنك! المعرفة ! = القدرة . يمكنك التدرب على حل المشكلات التي تتضمن الخوارزميات على HackerRank و LeetCode . غالبًا ما يتم استخدام المهام من هذه المواقع حتى أثناء المقابلات في Google وFacebook، لذلك لن تشعر بالملل بالتأكيد :) لتعزيز مادة الدرس هذه، أوصي بمشاهدة هذا الفيديو الممتاز حول تدوين O الكبير على YouTube. نراكم في الدروس القادمة! :)