ماكس كومة في جافا

الشجرة الثنائية

في جافا، هناك العديد من أنواع مختلفة من هياكل البيانات. تعتمد الكومة على بنية شجرة تسمى الشجرة الثنائية . تتكون الشجرة الثنائية من عقد، يمكن أن تحتوي كل منها على عقدتين فرعيتين كحد أقصى: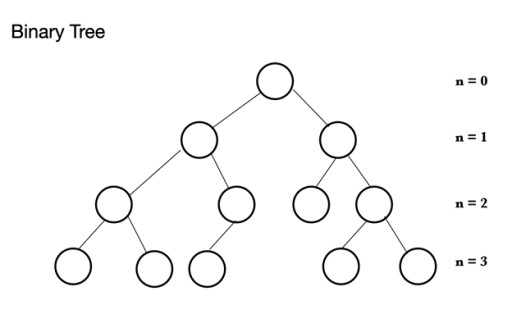 تتكون الشجرة الثنائية من عقدة أصلية يمكن أن تحتوي على عقدتين من 0 إلى عقدتين. يمكن أن تحتوي على عقدة فرعية يسرى و/أو عقدة فرعية يمينية، أو لا تحتوي على عقد على الإطلاق. في الشجرة الثنائية الكاملة، يتم ملء جميع العقد باستثناء المستوى الأخير الذي يمكن أن يكون ممتلئًا، ولكن لا يلزم أن يكون ممتلئًا. يمكن أن يحتوي المستوى الأخير، المستوى n، من 1 إلى 2n من العقد، حيث يكون الأول عند n = 0 وهو الجذر.

ماكس كومة

ماكس كومة (أو maxheap) هي شجرة ثنائية كاملة . الشيء المهم في الأمر هو أن العقدة الأصلية يجب أن يكون لها قيمة أكبر من أو تساوي قيمة العقد الفرعية اليمنى واليسرى. إذا لم يتم الالتزام بذلك، فلن يكون لديك الحد الأقصى للكومة. من ناحية أخرى، فإن الحد الأدنى للكومة هو العكس حيث يكون الجذر هو أصغر قيمة مع زيادة قيمة العقد المتعاقبة؛ كل عقدة فرعية لها قيمة أكبر من أو تساوي العقدة الأم. إنها أيضًا شجرة ثنائية كاملة. مثال على الحد الأقصى للكومة هو: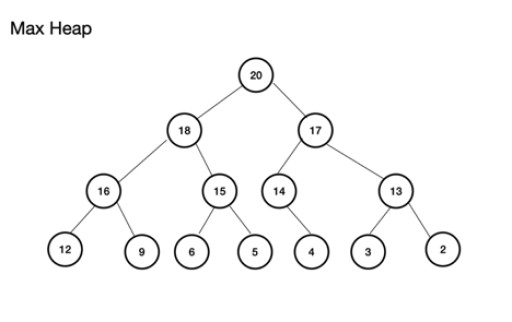 يمكن بناء الحد الأقصى للكومة من مصفوفة. سيتم التفكير في هذه المجموعة من حيث الشجرة. بالنسبة للكومة، إذا تم تخزين الجذر (العقدة الرئيسية العليا للشجرة) في الموضع (الفهرس) n، فسيتم تعريفه للمصفوفة، theArray ، باسم theArray[n] . وبالتالي، فإن العقدتين الفرعيتين اليمنى واليسرى موجودة في Array[2n+1] و TheArray[2n+2] على التوالي. بالنسبة إلى الكومة القصوى، يكون الجذر عند theArray[0] . بالنسبة للمستوى n، الجذر n = 0: theArr[n] هي العقدة الأصلية theArr[(2*n)+1] هي العقدة الفرعية اليسرى theArr[(2*n)+2] هي العقدة الفرعية اليمنى

فئة قائمة الانتظار ذات الأولوية

يمكن تنفيذ الأكوام في Java باستخدام فئة PriorityQueue . يتم استخدام PriorityQueues للعثور على العنصر الأكثر أو الأقل أهمية في المجموعة. يمكن العثور على فئة PriorityQueue في java.util.package . يجب أن تتكون قوائم الأولوية من كائنات قابلة للمقارنة بحيث يتم وضعها بترتيب معين في قائمة الانتظار. يمكن أن تحتوي PriorityQueue على مقارنة بحيث يتم إجراء مقارنة بين الكائنات وتشكيل قائمة الانتظار وفقًا لهذه المقارنة. مثال على ذلك هو:

import java.util.Comparator;
import java.util.PriorityQueue;

public class Main
{
    public static void main(String[] args) {
        // Create PriorityQueue with comparator for ascending order of array length
        PriorityQueue intQueue = new PriorityQueue((a,b) -> a - b);
        Integer [] array1 = {1, 2, 4, 6, 8, 9};
        Integer [] array2 = {3, 6, 9};
        Integer [] array3 = {2, 4, 8, 16, 32, 64, 128};
        Integer [] array4 = {5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55};
        Integer [] array5 = {4};

        //Add the array lengths to intQueue
        intQueue.add(array1.length);
        intQueue.add(array2.length);
        intQueue.add(array3.length);
        intQueue.add(array4.length);
        intQueue.add(array5.length);
        //Write out contents of intQueue as stored
        while (intQueue.size() != 0) {
            System.out.println(intQueue.remove());
        }
    }
}

إعطاء الإخراج: في هذا المثال، الحجم الافتراضي لـ intQueue هو 11، لذلك لم يتم ذكره (عادةً الوسيطة الأولى قبل المقارنة) وتم تقديم المقارنة على النحو التالي: سيؤدي هذا إلى إجراء مقارنة بين العناصر الموجودة في intQueue وفرزها إلى أطوال مصفوفة بترتيب تصاعدي.

تنفيذ PriorityQueue لإنشاء الحد الأقصى للكومة

يتم تعيين فئة PriorityQueue افتراضيًا على الحد الأدنى من الكومة بدون مقارنة. الحد الأدنى للكومة هو عكس الحد الأقصى للكومة وبالتالي فإن الجذر هو أصغر قيمة والعقد الفرعية المتعاقبة أكبر أو تساوي الجذر والعقد الأصلية اللاحقة. لهذا السبب، بالنسبة إلى الحد الأقصى من الكومة، من الضروري استخدام ReverseOrder() من إطار عمل مجموعات Java كمقارنة. سيضمن هذا حصولنا على الحد الأقصى للكومة وليس الحد الأدنى للكومة. تحتوي هذه الفئة على توابع مفيدة مثل add() و contains() و remove() و poll() و peek() . تتم إضافة العناصر إلى قائمة الانتظار ويمكن أن تكون بأي ترتيب. ستقوم قائمة انتظار PriorityQueue الجديدة بتخزين هذه العناصر كحد أقصى لكومة الذاكرة المؤقتة بترتيب عكسي. عند كتابة قائمة الانتظار، سيكون الترتيب كما يلي: الجذر-الطفل الأيسر مع الجذر كأصل (Left-child_1) الطفل الأيمن مع الجذر كأصل (Right-child_1) اليسار-الطفل مع Left-child_1 كأصل (Left-child_2) ) الطفل الأيمن مع Left-child_1 كوالد (Right-child_2) الطفل الأيسر مع Right-child_1 كوالد (Left-child_3) الطفل الأيمن مع Right-child_1 كوالد (Right-child_3) الطفل الأيسر مع Left-child_2 كوالد (Left-child_4) والطفل الأيمن مع Left-child_2 كوالد (Right-child_4)، وما إلى ذلك الكود التالي هو مثال لكيفية إنشاء الحد الأقصى للكومة (maxheap) في Java. أول شيء يجب فعله هو ملء المصفوفة بالقيم التي سيتم إنشاء الكومة القصوى لها. وهذا ما يسمى المصفوفة . بعد ذلك، يتم إنشاء PriorityQueue ، theQueue ، ثم تتم إضافة العناصر من theArray إلى هذا. يستخدم هذا الأسلوب add() ، على سبيل المثال theQueue.add(10) لإضافة 10 إلى نهاية قائمة الانتظار. لتوضيح بعض وظائف فئة PriorityQueue ، يتم بعد ذلك استخدام طريقة peek() للعثور على رأس الكومة، وهذه هي القيمة القصوى، في هذه الحالة، 99. المهمة التالية هي التحقق من حجم الكومة باستخدام size() الذي وجد أنه 9 ويتم طباعته على وحدة التحكم. تكتب الطريقة writeMaxHeap العناصر الموجودة في قائمة الانتظار بالترتيب من الجذر، والطفل الأيسر مع الجذر كوالد، والطفل الأيمن مع الجذر كوالد، والطفل الأيسر مع الطفل الأيسر الأول كوالد، والطفل الأيمن مع الطفل الأيسر الأول كـ الوالد، والطفل الأيمن مع الطفل الأيمن الأول كوالد، والطفل الأيسر مع الطفل الأيمن الأول كوالد، وما إلى ذلك، مع القيم اللاحقة التي تستخدم الأطفال الأيسر والأيمن كآباء بنفس الترتيب الموضح أعلاه. يتم استخدام طريقة PriorityQueue التي تحتوي على (J) لمعرفة ما إذا كان عنصر معين، J، موجودًا في قائمة الانتظار. في هذه الحالة نبحث عن J = 10. في مثالنا، صحيح أن هذا موجود في قائمة الانتظار لذا يتم كتابته إلى وحدة التحكم كصحيح. يتم بعد ذلك استخدام طريقة PriorityQueue أخرى لإزالة (J) لإزالة J = 10 من قائمة الانتظار . لتوضيح المزيد من وظائف PriorityQueue ، يتم استخدام طريقة poll() لإزالة عنصر الرأس (القيمة القصوى) باستخدام حلقة while ، مع إزالة عنصر الرأس في قائمة الانتظار الجديدة في كل مرة وتقليل حجم قائمة الانتظار بمقدار عنصر واحد في كل مرة. يحدث هذا في طريقة writeQueue التي يتم استدعاؤها من main. في كل مرة تتم طباعة العنصر الذي تمت إزالته على وحدة التحكم. لن تحتوي قائمة الانتظار الأصلية في النهاية على أي عناصر متبقية. العناصر المطبوعة هي الكومة القصوى بترتيب تنازلي للقيمة، حيث تتم طباعة رأس قائمة الانتظار في كل مرة.

mport java.util.Collections;
import java.util.PriorityQueue;

public class MaxHeap {

       public static void writeQueue(PriorityQueue<Integer> priorityQueue)
       {
           // Write out elements in queue, priorityQueue, and remove them using poll()
           while(priorityQueue.size() != 0)
           {
               System.out.println(priorityQueue.poll());
           }
       }

       public static void writeMaxHeap(PriorityQueue<Integer> priorityQueue)
       {
           // Write out elements in queue as a max heap - root, left child, right child, etc
           for (Integer element : priorityQueue) {
               System.out.println(element);
           }
       }

       public static void main(String args[])
       {
           // Array of numbers to create a max heap array from
           int[] theArray = {5, 3, 13, 10, 99, 19, 6, 51, 9};

           // theQueue is created
           PriorityQueue<Integer> theQueue =
                   new PriorityQueue<Integer>(Collections.reverseOrder());

           // Elements are added to theQueue
           for (int i = 0 ; i <theArray.length; ++i)
           {
               theQueue.add(theArray[i]);
           }

           // The head or root element (priority element) is printed out
           System.out.println("The root value is : " +  theQueue.peek());

           // Find size of theQueue. Use method size()
           Integer s = theQueue.size();
           System.out.println("Size of theQueue? " + s);

           // All elements of theQueue are printed in terms of parent,
           // left child, right child
           System.out.println("theQueue written using for loop:");
           writeMaxHeap(theQueue);

           // Does theQueue contain 10? Use method contains()
           boolean b = theQueue.contains(10);
           System.out.println("Does theQueue contain 10? " + b);

           // Erasing value 10 from array using remove()
           theQueue.remove(10);

           // All elements of theQueue are printed out and removed.
           // Each one is the maximum value left in the queue.
           // At the end theQueue will be empty
           System.out.println("theQueue written out using poll():");
           writeQueue(theQueue);

           // Find size of theQueue. Use method size()
           s = theQueue.size();
           System.out.println("Size of theQueue? " + s);
       }
   }

انتاج:

ماكس هيابيفي

يتم استخدام خوارزمية Max Heapify للتأكد من أن الشجرة الثنائية هي الحد الأقصى للكومة. إذا كنا عند عقدة، n، والعقد التابعة لها، اليسار واليمين، هي أيضًا الحد الأقصى للأكوام بحد ذاتها، فهذا رائع، لدينا الحد الأقصى للكومة. إذا لم يكن هذا هو الحال في جميع أنحاء الشجرة، فلن يكون لدينا الحد الأقصى للكومة. يتم استخدام خوارزمية Max Heapify لفرز الشجرة بحيث تلتزم بمبادئ maxheap. يعمل Max Heapify على عقدة واحدة فقط. إذا كان المتطلب هو أن يكون المصفوفة عبارة عن مصفوفة ذات الحد الأقصى للكومة، فيجب تحويل جميع الأشجار الفرعية إلى الحد الأقصى للكومة قبل الجذر، واحدة تلو الأخرى. يجب استخدام الخوارزمية في كل عقدة. سيتم ذلك على العقد N/2 (ستلتزم الأوراق بالحد الأقصى لمتطلبات الكومة). التعقيد الزمني للكومة هو O(NlogN)، وبالنسبة لعقدة واحدة عند الارتفاع X، يكون التعقيد الزمني هو O(X). يوضح التعليمة البرمجية التالية كيفية تكديس شجرة (مصفوفة) إلى الحد الأقصى.

public class MaxHeapify

{
   public static Integer[] maxHeapify(Integer[ ] array, Integer i)
   {
       // Create left-child and right-child for the node in question
       Integer leftChild = 2 * i + 1;
       Integer rightChild = 2 * i + 2;

       // Assign maxVal to parent node, i
       Integer maxVal = i;

       // Set maxVal to greater of the two: node or left-child
       if( leftChild < array.length && array[leftChild] > array[maxVal] )
           maxVal = leftChild;

       // Set maxVal to greater of the two: maxVal or right-child
       if( rightChild < array.length && array[rightChild] > array[maxVal] )
           maxVal = rightChild;

       // Check if maxVal is not equal to parent node, then set parent node to
       // maxVal, swap values and then do a maxheapify on maxVal
       // which is now the previous parent node
       if( maxVal != i )
       {
           Integer value = array[i];
           array[i] = array[maxVal];
           array[maxVal] = value;
           array = maxHeapify(array, maxVal);
       }

       return array;
   }


   public static Integer[] maxHeapCreate(Integer array[])
   {
       // Call maxHeapify to arrange array in a max heap
       Integer [] theNewArr = array;
       for( Integer i = array.length/2; i >= 0; i-- )
           theNewArr = maxHeapify(array, i);

       return theNewArr;
   }

   public static void main(String[] args)
   {
       // Create array to be maxheapified, theArray,
       // and array, newArray, to write results into, by calling maxheapCreate
       // newArray will now be a maxheap
       Integer[] theArray = {5, 3, 13, 10, 99, 19, 6, 51, 9};
       Integer[ ] newArray = maxHeapCreate(theArray);

       // Print out contents of newArray
       System.out.println("newArray:");
       for(int i = 0; i < newArray.length; ++i)
       {
           System.out.println(newArray[i]);
       }

       // Print out labelled contents of newArray
       System.out.println(" root : " + newArray[0]);
       for (int i = 0; i <= newArray.length/2 - 1; i++) {
           System.out.print(" parent node : " + newArray[i] + " left child : " +
                            newArray[(2*i)+1] + " right child :" + newArray[(2*i)+2]);
           System.out.println();
       }
  }
}

إعطاء الإخراج: في هذا الكود، يتم إنشاء المصفوفة وملؤها بالأرقام. يتم إنشاء مصفوفة ثانية، newArray ، وهذه المرة ستحتوي على نتيجة الطريقة، maxheapCreate ، مصفوفة الكومة القصوى. يتم استدعاء الأسلوب maxHeapCreate من main ، وهنا يتم إنشاء مصفوفة جديدة، theNewArr ، وملؤها بنتائج maxHeapify . يتم ذلك عن طريق تنفيذ حلقات تزيد عن نصف حجم مصفوفة الإدخال. لكل تمريرة من الحلقة، يتم استدعاء الطريقة maxHeapify بدءًا من العنصر الموجود في منتصف المصفوفة وانتهاءً بالعنصر الأول. لكل استدعاء لـ maxHeapify ، يتم العثور على الطفل الأيسر والطفل الأيمن للعقدة الأصلية، i، ويتم إجراء عمليات التحقق للعثور على الأكبر من بين الثلاثة، مع تحديد ذلك على أنه maxVal . إذا كان maxVal لا يساوي العقدة الأصلية، فسيتم إجراء مبادلة بحيث يتم تبديل العقدة الأصلية و maxVal ثم يتم استدعاء maxHeapify مرة أخرى هذه المرة على maxVal ويتم تنفيذ نفس الخطوات كما كان من قبل. في النهاية سيتم إنشاء الحد الأقصى للكومة ولن يكون هناك المزيد من التكرارات لتنفيذها. يتم الآن إرجاع المصفوفة المحدثة، array ، إلى main باسم newArray ثم تتم طباعة كل عنصر متتالي على وحدة التحكم. newArray الآن هو الحد الأقصى للكومة. لاحظ أنه كما في المثال السابق باستخدام PriorityQueue ، يتم كتابة الأرقام: الجذر، الطفل الأيمن للجذر كوالد، الطفل الأيسر للجذر كوالد، الطفل الأيمن للجذر الأول كوالد، الطفل الأيسر للجذر الأول الطفل الأيسر كوالد، والطفل الأيمن للطفل الأيسر الأول كوالد، والطفل الأيسر للطفل الأول الأيمن كوالد، وما إلى ذلك. وهي بترتيب مختلف قليلاً عن تلك عند استخدام PriorityQueue لأن المقارنة تتم بين العناصر المتتالية بينما في مثال maxheapify، تتم مقارنة العقدة بالعنصرين المتتاليين التاليين في المصفوفة ويتم تبديلها للحصول على القيمة الأكبر. باختصار، يتم استخدام خوارزميتين مختلفتين. كلاهما ينشئان الحد الأقصى للكومة.

خاتمة

لقد نظرنا هنا إلى الحد الأقصى للكومة وكيف يمكن إنشاؤها باستخدام خوارزمية PriorityQueue أو Max Heapify. يعد استخدام PriorityQueue مع ReverseOrder() ‎ طريقة رائعة للقيام بذلك وهي الطريقة الموصى بها. ومع ذلك، يمكنك دراسة هذه الأمثلة وكتابة الأساليب الخاصة بك لأن هذا سيكون تمرينًا جيدًا للبرمجة يساعدك على النجاح في مقابلتك لـ Java Junior.