تم تصميم خوارزميات البحث المختلفة لمهام مختلفة. سنتحدث اليوم عن بحث A*، وهو أحد أكثر خوارزميات تحديد المسار فعالية. يعد هذا الخيار مناسبًا جدًا لألعاب الكمبيوتر وبناء الرسوم البيانية للبحث مثل الطرق بين المدن وما إلى ذلك. ربما لاحظت، على سبيل المثال، في ألعاب الفيديو الإستراتيجية أو التكتيكية، كيف أنه بعد الضغط على زر، يبدأ لاعبك أو مجموعتك على الفور دون تأخير في عبور الملعب إلى النقطة التي حددتها. لا يوجد تأخير على وجه التحديد لأن الألعاب تستخدم خوارزميات فعالة تحسب بالضبط كيف يحتاج اللاعب للوصول إلى مكان ما. أو عدو يجد اللاعب بشكل لا لبس فيه ويبدأ بالسير في الاتجاه الصحيح من بعيد. عادة، يتم استخدام خوارزمية A* لمثل هذه الإجراءات.
ما هي خوارزمية أ*
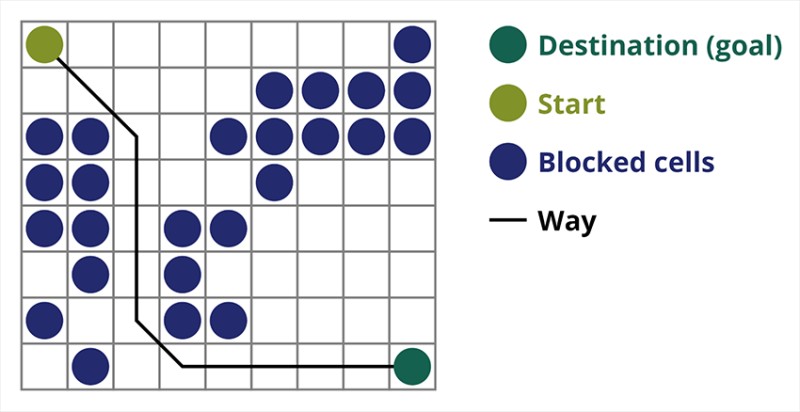
تعد خوارزمية اكتشاف المسار A* مثالاً على خوارزمية البحث الأفضل أولاً. الغرض من خوارزمية A* هو العثور على مسار من نقطة إلى أخرى. إنها واحدة من الكلاسيكيات للبحث في خوارزميات الرسم البياني. دعونا معرفة كيف يعمل باستخدام مثال. تخيل لعبة ثنائية الأبعاد مع عرض من أعلى إلى أسفل. دعونا نقسم منطقة لعبتنا إلى مربعات جشع، على سبيل المثال 8*8 خلايا مثل رقعة الشطرنج. يمكن أن تكون خلايانا واحدة من نوعين، سالكة أو سالكة (عائق). في كل فترة زمنية يقوم اللاعب أو العدو الذي يقترب من اللاعب بتحريك خلية واحدة. في الألعاب، يمكن أن تكون الخلايا القابلة للعبور ذات طبيعة مختلفة، على سبيل المثال، طريق مسطح أو عشب أو رمل، وهو ما يحدد صعوبة التحرك عليها، ولكن للتبسيط سنفترض أن جميع الخلايا القابلة للعبور يتم تمريرها بنفس الطريقة. في الصورة أدناه، الخلايا الزرقاء هي العوائق.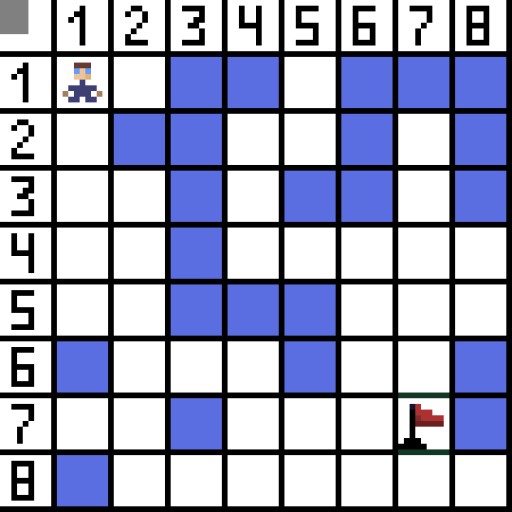
لنقم بتعيين خلية واحدة (أو عقدة) كخلية البداية (الحرف موجود فيها)، والخلية الأخرى كخلية هدف أو خلية هدف (تلك التي تحمل العلم)، ونصف كيفية عمل خوارزمية A* في هذه الحالة. الحرف موجود في الخلية (1،1) والهدف موجود في الخلية (7،7). تحتوي كل خلية على جيران أفقي ورأسي وقطري. يعتمد ذلك على اللعبة، إذا قمنا بحساب العقد القطرية أم لا. على سبيل المثال، في العديد من الألعاب ذات العرض من أعلى إلى أسفل مثل Bomberman أو Pacman، يمكن للشخصيات التحرك أفقيًا أو رأسيًا فقط. في هذه الحالة، كل عقدة، باستثناء لمس الحواف، لديها 4 جيران فقط. إذا كنا نتحدث عن لعبة حيث يمكن للشخصيات التحرك قطريًا، فيمكن أن تحتوي كل عقدة على ما يصل إلى 8 جيران. في الخطوة الأولى من الخوارزمية، تحتوي الخلية التي يقع فيها الحرف على جارتين. بتعبير أدق، ثلاثة، ولكن واحد منهم يشكل عائقا. 
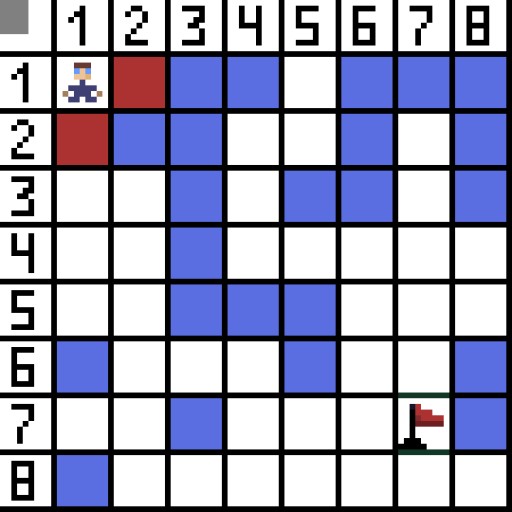ومن الواضح أن الطريق القطري أطول. إذا جعلنا جانب الخلية يساوي واحدًا شرطيًا، فإن طول قطر هذه الخلية يساوي الجذر التربيعي لاثنين. وهذا ما تقوله نظرية فيثاغورس. للانتقال من الخلية A إلى الخلية B، يجب عليك أولاً تحديد إحدى الخلايا المجاورة، ثم الخلية التالية، وهكذا. افهم أيضًا على طول الطريق ما إذا كان من الممكن الانتقال من الخلية الأولية إلى الخلية المستهدفة. تختار خوارزمية A* في كل خطوة إحدى الخلايا المجاورة وفقًا لقيمة الدالة F. تقيس هذه الدالة مدى جودة الخلية المرشحة التي سيتم تضمينها في أقصر مسار لدينا. هذه هي دالة التكلفة، وهي مجموع دالة النقل G والدالة الإرشادية.
-
تكلفة G — هي المسافة من نقطة البداية.
-
تكلفة H (الاستدلال) هي المسافة من عقدة النهاية (الهدف). يمكن أن تكون هذه الوظيفة مختلفة، حيث يقرر المطور ما هو الأفضل. ربما يكون اختيار H هو الأكثر أهمية في A*، وهذه هي النقطة التي تجعل أي تطبيق معين للخوارزمية أكثر أو أقل فعالية. من الناحية النظرية يمكنك استخدام أي وظيفة تريدها.
في حالتنا، نحن نعرف موضع الخلية المستهدفة ويمكننا، على سبيل المثال، حساب المسافة الإقليدية الهندسية بين الخلية المستهدفة والحالية. كلما قصرت المسافة كلما اقتربنا من الهدف.
-
تكلفة F = G + H. لذا تحسب الخوارزمية تكاليف جميع العقد المجاورة F وتختار واحدة من أقل تكاليف F للنظر إليها أولاً. عندما نختار واحدة، نضع علامة عليها على أنها مغلقة ونحسب القيم لهذه العقدة المجاورة.
دالة إرشاديةكيف يمكننا حساب H؟
هذه هي وظيفة ارشادية. الاسم نفسه يعني أنه يتم تحديده بالتجربة، ويمكن أن يكون مختلفًا. وهنا سنأخذها مساوية لما يسمى بالمسافة الإقليدية بين النقطتين (x1, y1) و (x2, y2):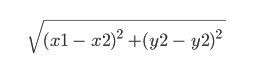
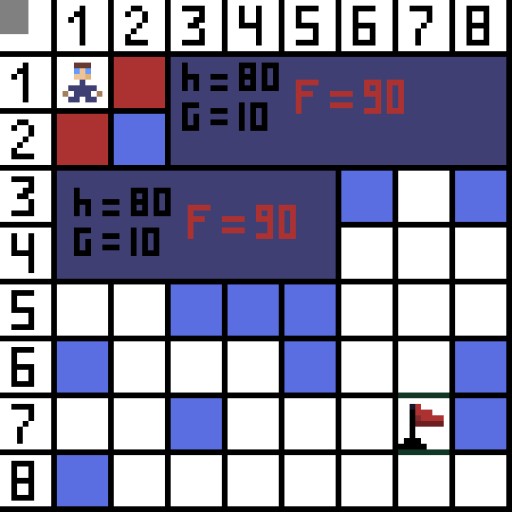في الصورة، للخطوة الأولى، هناك خياران، وهما متساويان في التكلفة، ولكن في الخطوة التالية، تدخل الشخصية في طريق مسدود في أحد الخيارات. ولذلك، فإننا نسير في الاتجاه الآخر. في التكرار التالي، لدينا بالفعل 4 خيارات. 
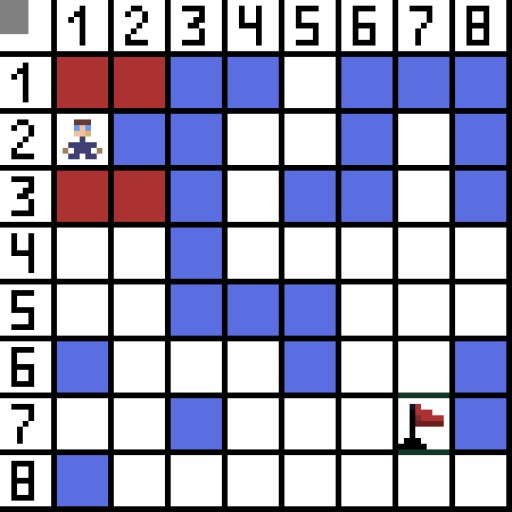اثنان منهم غير مناسبين، لأنهما يؤديان إلى الخلف، والخيارات الأخرى جيدة بنفس القدر، لكن الخوارزمية قررت أنه من الأفضل الانتقال قطريًا إلى الخلية (3،2). علاوة على ذلك، في كل خطوة، يتم تكرار حساب الدالة F حتى يصل الحرف إلى الخلية المستهدفة. إذا، بالطبع، مثل هذا المقطع موجود. 
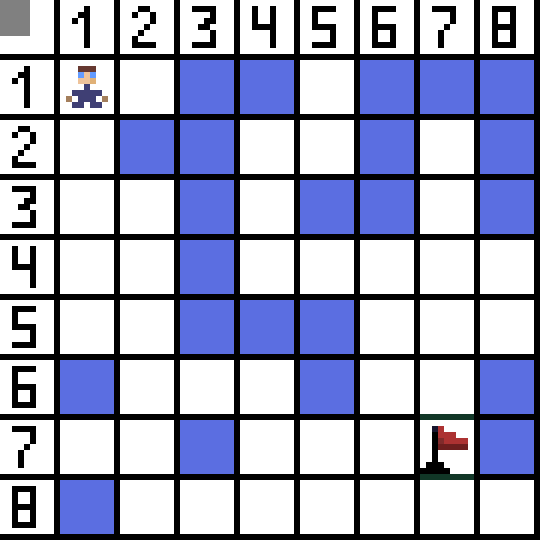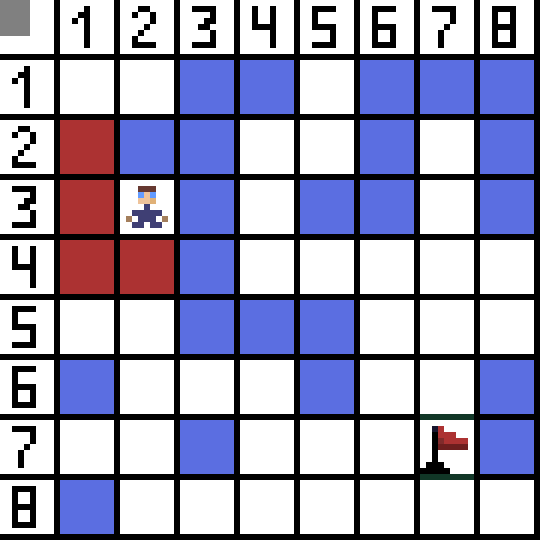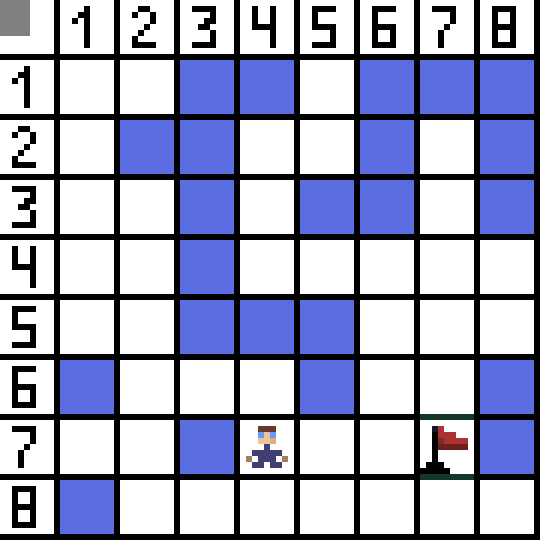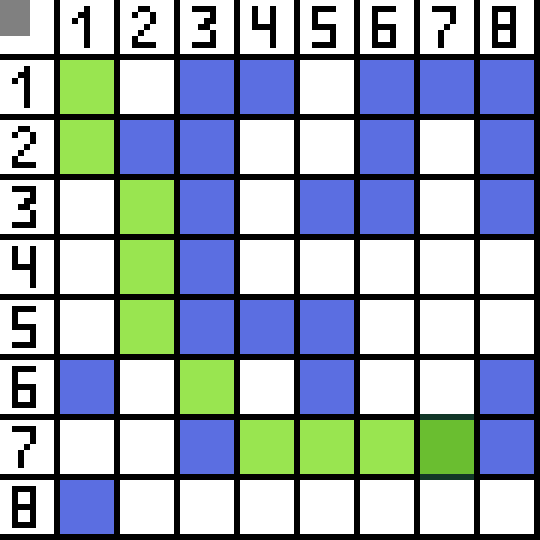يشير المسار الأخضر في الصورة المتحركة إلى المسار الأمثل للشخصية إلى العلامة.
أ* الخوارزمية خطوة بخطوة
لتنفيذ الخوارزمية في Java، يتعين عليك اتخاذ الخطوات التالية 1. تحتاج أولاً إلى إنشاء قائمتين للعقد المفتوحة والعقد المغلقة. 2. تهيئة كلتا القائمتين. في القائمة المغلقة، تشير عقدة البداية إلى القائمة المفتوحة. 3. بينما توجد عناصر في القائمة المفتوحة: 3أ. ابحث عن العقدة min ذات أصغر F 3b. إزالة دقيقة من القائمة المفتوحة 3C. تحديد الجيران على الأقل (حتى 8، إذا تم أخذ الأقطار بعين الاعتبار) ثلاثي الأبعاد. التحقق من كل جار: أ) إذا كان الجار هو الخلية المستهدفة، توقف عن البحث ب) إذا لم يكن الأمر كذلك، فاحسب G، H لها. G = min.G + المسافة بين الجار وmin F = G + H c) إذا كانت العقدة التي لها نفس موضع الجار في القائمة المفتوحة وكانت F أقل من الجار، فتخطي ذلك الجار d) إذا العقدة التي لها نفس موضع الجار موجودة في القائمة المغلقة، و f أقل من الجار، تخطي هذا الجار. بخلاف ذلك، أضف العقدة إلى القائمة المفتوحة نهاية الحلقة الداخلية 3e. إضافة دقيقة إلى القائمة المغلقة نهاية الحلقة الخارجية لذلك، في كل تكرار سنقوم بالإجراء التالي:- حدد الخلية من قائمتنا المفتوحة ذات أقل مجموع نقاط مقدر.
- قم بإزالة هذه الخلية من القائمة المفتوحة.
- أضف جميع الخلايا التي يمكننا الوصول إليها منها إلى القائمة المفتوحة.
- عندما نفعل ذلك، نقوم أيضًا بمعالجة النتيجة الجديدة من تلك العقدة إلى كل واحدة جديدة لمعرفة ما إذا كان ذلك يمثل تحسينًا عما لدينا حتى الآن، وإذا كان الأمر كذلك، فإننا نقوم بتحديث ما نعرفه عن تلك الخلية.
أ* الكود الزائف
فيما يلي رمز زائف مختصر لـ A* pathfinding:Input: a grid with locked and empty cells, with start and goal cell.
Output: least cost path from start to goal cell.
Initialisation
openList = {startCell} //list of traversed cells
closedList = {} //list of already traversed cells
g.startCell = 0 //cost from source cell to a cell
h.startCell = h(startCell, goal) //heuristic
f.startCell = g.startCell + h.StartCell
while openList is not empty
do
//let the currentCell equal the cell with the least f value
currentCell = Cell on top of openList, with least f
if currentCell == end return
remove currentCell from openList
add currentCell to closedList
foreach n in child.currentCell
if n in closedList
continue
cost = g.currentCell + distance(currentCell,n)
if (n in openList and cost < g.n)
remove n from closedList
g.n = cost
h.n = h(n, goal)
f.n = g.n + h.nمن الكود الكاذب إلى تنفيذ A * في Java
A* يجب أن يكون لدى Pathfinding في تحقيق Java بعض الطرق لخدمة الخوارزمية:- الخلية، وهي بنية تحتوي على المعلمات الضرورية
- القوائم المفتوحة والمغلقة
- طريقة لحساب وظيفة ارشادية
- طريقة لتتبع المسار من المصدر إلى الوجهة
- طرق التحقق مما إذا كانت الخلية المحددة محظورة، وما إذا كان قد تم الوصول إليها بالفعل، وما إذا كانت صالحة، وما إلى ذلك
package Asterist;
import java.util.PriorityQueue;
import java.util.Stack;
public class AAsterisk {
//Java Program to implement A* Search Algorithm
//Here we're creating a shortcut for (int, int) pair
public static class Pair {
int first;
int second;
public Pair(int first, int second){
this.first = first;
this.second = second;
}
@Override
public boolean equals(Object obj) {
return obj instanceof Pair && this.first == ((Pair)obj).first && this.second == ((Pair)obj).second;
}
}
// Creating a shortcut for tuple<int, int, int> type
public static class Details {
double value;
int i;
int j;
public Details(double value, int i, int j) {
this.value = value;
this.i = i;
this.j = j;
}
}
// a Cell (node) structure
public static class Cell {
public Pair parent;
// f = g + h, where h is heuristic
public double f, g, h;
Cell()
{
parent = new Pair(-1, -1);
f = -1;
g = -1;
h = -1;
}
public Cell(Pair parent, double f, double g, double h) {
this.parent = parent;
this.f = f;
this.g = g;
this.h = h;
}
}
// method to check if our cell (row, col) is valid
boolean isValid(int[][] grid, int rows, int cols,
Pair point)
{
if (rows > 0 && cols > 0)
return (point.first >= 0) && (point.first < rows)
&& (point.second >= 0)
&& (point.second < cols);
return false;
}
//is the cell blocked?
boolean isUnBlocked(int[][] grid, int rows, int cols,
Pair point)
{
return isValid(grid, rows, cols, point)
&& grid[point.first][point.second] == 1;
}
//Method to check if destination cell has been already reached
boolean isDestination(Pair position, Pair dest)
{
return position == dest || position.equals(dest);
}
// Method to calculate heuristic function
double calculateHValue(Pair src, Pair dest)
{
return Math.sqrt(Math.pow((src.first - dest.first), 2.0) + Math.pow((src.second - dest.second), 2.0));
}
// Method for tracking the path from source to destination
void tracePath(
Cell[][] cellDetails,
int cols,
int rows,
Pair dest)
{ //A* Search algorithm path
System.out.println("The Path: ");
Stack<Pair> path = new Stack<>();
int row = dest.first;
int col = dest.second;
Pair nextNode = cellDetails[row][col].parent;
do {
path.push(new Pair(row, col));
nextNode = cellDetails[row][col].parent;
row = nextNode.first;
col = nextNode.second;
} while (cellDetails[row][col].parent != nextNode); // until src
while (!path.empty()) {
Pair p = path.peek();
path.pop();
System.out.println("-> (" + p.first + "," + p.second + ") ");
}
}
// A main method, A* Search algorithm to find the shortest path
void aStarSearch(int[][] grid,
int rows,
int cols,
Pair src,
Pair dest)
{
if (!isValid(grid, rows, cols, src)) {
System.out.println("Source is invalid...");
return;
}
if (!isValid(grid, rows, cols, dest)) {
System.out.println("Destination is invalid...");
return;
}
if (!isUnBlocked(grid, rows, cols, src)
|| !isUnBlocked(grid, rows, cols, dest)) {
System.out.println("Source or destination is blocked...");
return;
}
if (isDestination(src, dest)) {
System.out.println("We're already (t)here...");
return;
}
boolean[][] closedList = new boolean[rows][cols];//our closed list
Cell[][] cellDetails = new Cell[rows][cols];
int i, j;
// Initialising of the starting cell
i = src.first;
j = src.second;
cellDetails[i][j] = new Cell();
cellDetails[i][j].f = 0.0;
cellDetails[i][j].g = 0.0;
cellDetails[i][j].h = 0.0;
cellDetails[i][j].parent = new Pair( i, j );
// Creating an open list
PriorityQueue<Details> openList = new PriorityQueue<>((o1, o2) -> (int) Math.round(o1.value - o2.value));
// Put the starting cell on the open list, set f.startCell = 0
openList.add(new Details(0.0, i, j));
while (!openList.isEmpty()) {
Details p = openList.peek();
// Add to the closed list
i = p.i; // second element of tuple
j = p.j; // third element of tuple
// Remove from the open list
openList.poll();
closedList[i][j] = true;
// Generating all the 8 neighbors of the cell
for (int addX = -1; addX <= 1; addX++) {
for (int addY = -1; addY <= 1; addY++) {
Pair neighbour = new Pair(i + addX, j + addY);
if (isValid(grid, rows, cols, neighbour)) {
if(cellDetails[neighbour.first] == null){ cellDetails[neighbour.first] = new Cell[cols]; }
if (cellDetails[neighbour.first][neighbour.second] == null) {
cellDetails[neighbour.first][neighbour.second] = new Cell();
}
if (isDestination(neighbour, dest)) {
cellDetails[neighbour.first][neighbour.second].parent = new Pair ( i, j );
System.out.println("The destination cell is found");
tracePath(cellDetails, rows, cols, dest);
return;
}
else if (!closedList[neighbour.first][neighbour.second]
&& isUnBlocked(grid, rows, cols, neighbour)) {
double gNew, hNew, fNew;
gNew = cellDetails[i][j].g + 1.0;
hNew = calculateHValue(neighbour, dest);
fNew = gNew + hNew;
if (cellDetails[neighbour.first][neighbour.second].f == -1
|| cellDetails[neighbour.first][neighbour.second].f > fNew) {
openList.add(new Details(fNew, neighbour.first, neighbour.second));
// Update the details of this
// cell
cellDetails[neighbour.first][neighbour.second].g = gNew;
//heuristic function cellDetails[neighbour.first][neighbour.second].h = hNew;
cellDetails[neighbour.first][neighbour.second].f = fNew;
cellDetails[neighbour.first][neighbour.second].parent = new Pair( i, j );
}
}
}
}
}
}
System.out.println("Failed to find the Destination Cell");
}
// test
public static void main(String[] args) {
//0: The cell is blocked
// 1: The cell is not blocked
int[][] grid = {
{ 1, 1, 0, 0, 1, 0, 0, 0 },
{ 1, 0, 0, 1, 1, 0, 1, 0 },
{ 1, 1, 0, 1, 0, 0, 1, 0 },
{ 1, 1, 0, 1, 1, 1, 1, 1 },
{ 1, 1, 0, 0, 0, 1, 1, 1 },
{ 0, 1, 1, 1, 0, 1, 1, 0 },
{ 1, 1, 0, 1, 1, 1, 1, 0 },
{ 0, 1, 1, 1, 1, 1, 1, 1 }
};
// Start is the left-most upper-most corner
Pair src = new Pair(0,0);
//(8, 0);
// Destination is the right-most bottom-most corner
Pair dest = new Pair(6, 6);
AAsterisk app = new AAsterisk();
app.aStarSearch(grid, grid.length , grid[0].length, src, dest);
}
}
المسار: -> (0,0) -> (1,0) -> (2,1) -> (3,1) -> (4,1) -> (5,2) -> (5, 3) -> (6,4) -> (6,5) -> (6,6)
ويمكن ملاحظة أن هذا هو أحد أقصر الطرق التي يمكن بناؤها بين هاتين النقطتين. لاحظ أن الخطوة السادسة في مثالنا في الصورة وفي مخرجات البرنامج مختلفة، على الرغم من أن المسارات متساوية في الفعالية. يختار البرنامج أحد الخيارات الأكثر فعالية.
GO TO FULL VERSION