جاوا مرتب سازی حبابی

اگر تا به حال در مورد روش های مرتب سازی در برنامه نویسی شنیده اید، به احتمال زیاد این الگوریتم مرتب سازی حبابی بوده است. معروف است. هر برنامه نویسی مرتب سازی حبابی را می داند (یا حداقل در حین یادگیری درباره آن شنیده است) نه به این دلیل که بهترین الگوریتم مرتب سازی در جهان است، بلکه ساده ترین الگوریتم است. این الگوریتم معمولاً برای اهداف یادگیری استفاده می شود یا ممکن است آن را به عنوان یک کار در مصاحبه Java Junior خود دریافت کنید. درک الگوریتم مرتب‌سازی حباب جاوا بسیار آسان است، اما الگوریتم کارآمدی نیست. به هر حال بیایید بفهمیم.

مرتب سازی چیست

اول از همه، باید بفهمید مرتب سازی به طور کلی چیست و چه چیزی را می توانیم در برنامه های جاوا مرتب کنیم. اگر بتوانیم دو یا چند عنصر یا شی را با هر یک از ویژگی هایشان مقایسه کنیم، به این معنی است که می توان آنها را بر اساس این ویژگی مرتب کرد. مثلاً اعداد به ترتیب صعودی یا نزولی یا کلمات بر اساس حروف الفبا. از این رو، عناصر باید با یکدیگر قابل مقایسه باشند. به هر حال، عناصر چیست؟ در جاوا می توانیم عناصر مجموعه ها را با هم مقایسه کنیم. به عنوان مثال می توانیم Array یا ArrayList از اعداد صحیح، رشته ها و غیره را مرتب کنیم.

مرتب سازی حبابی چگونه کار می کند

فرض کنید، باید آرایه ای از اعداد صحیح را به ترتیب صعودی مرتب کنیم، یعنی از کوچکترین به بزرگترین عدد. ابتدا کل آرایه را طی می کنیم و هر 2 عنصر همسایه را با هم مقایسه می کنیم. اگر ترتیب نامناسبی داشته باشند (همسایه چپ بزرگتر از سمت راست است) آنها را با هم عوض می کنیم. در اولین پاس در انتها بزرگترین عنصر ظاهر می شود (اگر به ترتیب صعودی مرتب کنیم). ممکن است بگویید، بزرگترین عنصر "پاپ می شود". این دلیل نام الگوریتم مرتب سازی حباب است. مرحله اول را از عنصر اول تا آخرین عنصر تکرار می کنیم. ما دومین عنصر بزرگ را در جایگاه بعدی داریم. و غیره. با بررسی اینکه آیا حداقل یک مبادله در مرحله قبل انجام شده است، می توانیم یک الگوریتم را کمی بهبود دهیم. اگر اینطور نیست، اجرای خود را در امتداد آرایه متوقف می کنیم.

نمونه مرتب سازی حبابی

بیایید آرایه اعداد صحیح را مرتب کنیم، یکی که ممکن است در تصویر زیر مشاهده کنید. مرحله 1: در حال گذر از آرایه هستیم. الگوریتم با دو عنصر اول (با شاخص های 0 و 1)، 8 و 7 شروع می شود و بررسی می کند که آیا ترتیب صحیحی دارند یا خیر. بدیهی است، 8 > 7، بنابراین ما آنها را با هم عوض می کنیم. بعد، ما به عناصر دوم و سوم (شاخص های 1 و 2) نگاه می کنیم، حالا اینها 8 و 1 هستند. به همین دلایل، آنها را با هم عوض می کنیم. برای سومین بار 8 و 2 و حداقل 8 و 5 را با هم مقایسه می کنیم. در مجموع چهار مبادله انجام دادیم: (8، 7)، (8، 1)، (8، 2) و (8، 5). مقدار 8، بزرگترین در این آرایه، در انتهای لیست به موقعیت صحیح ظاهر می شود. 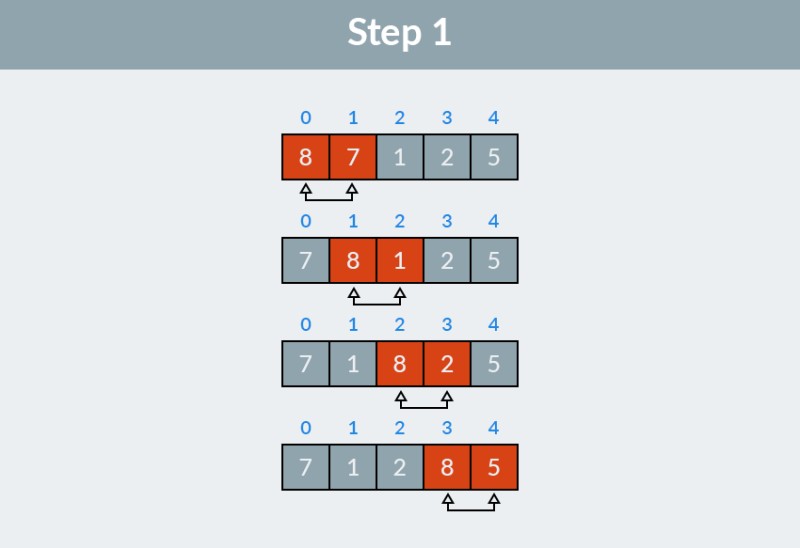نتیجه مرحله اول کار الگوریتم مرتب سازی حباب، آرایه بعدی است: مرحله 2. همین کار را با (7،1)، (7،2) و (7،5) انجام دهید. 7 اکنون در موقعیت ماقبل آخر است و نیازی به مقایسه آن با "دم" لیست نیست، قبلا مرتب شده است. نتیجه مرحله دوم کار الگوریتم مرتب‌سازی حبابی، آرایه بعدی است: همانطور که می‌بینید، این آرایه قبلا مرتب شده است. به هر حال الگوریتم مرتب‌سازی حبابی باید حداقل یک بار دیگر راه‌اندازی شود. مرحله 3. ما یک بار دیگر در حال عبور از آرایه هستیم. در اینجا چیزی برای تعویض وجود ندارد، بنابراین اگر از الگوریتم مرتب‌سازی حباب «بهبود» استفاده می‌کنیم (با بررسی اینکه آیا حداقل یک تبادل در مرحله قبل انجام شده است) این مرحله آخرین مرحله است.

کد جاوا مرتب سازی حباب

تحقق جاوا مرتب سازی حبابی

بیایید دو روش برای مرتب سازی حباب ایجاد کنیم. اولین مورد، bubbleSort(int[] myArray) یک صفحه است. هر بار از طریق آرایه اجرا می شود. مورد دوم، optimizedBubbleSort(int myArray[]) با متوقف کردن الگوریتم در صورتی که حلقه داخلی باعث تعویض نشد، بهینه می‌شود. شمارنده به شما نشان می دهد که در حین مرتب سازی چند مرحله انجام داده اید. در اینجا ما تحقق جاوا مرتب سازی حبابی را داریم:

import java.util.Arrays;

public class BubbleSortExample {

   //  Plane Bubble sort example

   public static int[] bubbleSort(int[] myArray) {

       int temp = 0;  //  temporary element for swapping
       int counter = 0;  //  element to count quantity of steps

       for (int i = 0; i < myArray.length; i++) {
           counter = i + 1;
           for (int j = 1; j < (myArray.length - i); j++) {

               if (myArray[j - 1] > myArray[j]) {
                   //  swap array’s elements using temporary element
                   temp = myArray[j - 1];
                   myArray[j - 1] = myArray[j];
                   myArray[j] = temp;
               }
           }
       }
       System.out.println("Steps quantity, non optimized = " + counter);
       return myArray;
   }
   //  An optimized version of Java Bubble Sorting

   static int[] optimizedBubbleSort(int myArray[]) {
       int temp;
       boolean swapped;
       int counter = 0;  //  element to count quantity of steps
       for (int i = 0; i < myArray.length - 1; i++) {
           counter = i + 1;
           swapped = false;
           for (int j = 0; j < myArray.length - i - 1; j++) {
               //  counter++;
               if (myArray[j] > myArray[j + 1]) {
                   //  swap arr[j] and arr[j+1]
                   temp = myArray[j];
                   myArray[j] = myArray[j + 1];
                   myArray[j + 1] = temp;
                   swapped = true;

               }
           }  //  counter = i;
           //  If there weren't elements to swap in inner loop, then break
           if (swapped == false) {

               break;

           }
       }
       System.out.println("steps quantity, optimized = " + counter);
       return myArray;
   }


   public static void main(String[] args) {
       int arr[] = {8, 7, 1, 2, 5};
       int arr1[] = {8, 7, 1, 2, 5};

       System.out.println("Array arr Before Bubble Sort");
       //  we use java.util.Arrays toString method to print the array
 System.out.println(Arrays.toString(arr));

       System.out.println("Array arr After Bubble Sort");
       System.out.println(Arrays.toString(bubbleSort(arr)));

       System.out.println("Array arr1 Before Bubble Sort");
       System.out.println(Arrays.toString(arr1));

       System.out.println("Array arr1 After Optimized Bubble Sort");
       System.out.println(Arrays.toString(optimizedBubbleSort(arr1)));
   }
}

نتیجه کار الگوریتم جاوا مرتب سازی حباب:

Array arr Before Bubble Sort
[8, 7, 1, 2, 5]
Array arr After Bubble Sort
Steps quantity, non optimized = 5
[1, 2, 5, 7, 8]
Array arr1 Before Bubble Sort
[8, 7, 1, 2, 5]
Array arr1 After Optimized Bubble Sort
steps quantity, optimized = 3
[1, 2, 5, 7, 8]

مرتب سازی حبابی چقدر کارآمد است؟

مرتب‌سازی حبابی یکی از ساده‌ترین الگوریتم‌ها برای پیاده‌سازی است، اما کارآمد نیست. به یک جفت حلقه تو در تو نیاز دارد. حتی در یک نسخه بهینه از الگوریتم در بدترین حالت (هر عنصر مجموعه داده به ترتیب معکوس مورد نظر است) حلقه بیرونی یک بار برای هر یک از n عنصر مجموعه داده تکرار می شود. حلقه داخلی n برابر برای بار اول، ( n-1 ) برای بار دوم، و غیره تکرار می شود. از این رو، برای مرتب کردن همه n عناصر، حلقه ها باید n*(n-1)/2 بار اجرا شوند. این پیچیدگی زمانی O(n2 ⁾ را می نامد و به این معنی است که الگوریتم حدود 500000 مقایسه را برای 1000 عنصر یک آرایه انجام می دهد. با این حال، الگوریتم مرتب‌سازی حبابی در استفاده از حافظه بسیار مؤثر است (پیچیدگی حافظه O(n) است ) و برای مجموعه‌های داده کوچک تقریباً مرتب‌شده واقعاً خوب است.