درخت دودویی
در جاوا، انواع مختلفی از ساختارهای داده وجود دارد. پشته بر اساس ساختار درختی به نام درخت باینری است . یک درخت دودویی از گره‌هایی تشکیل شده است که هر کدام می‌توانند حداکثر 2 گره فرزند داشته باشند: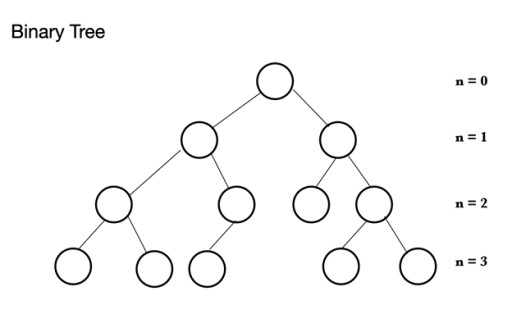
یک درخت باینری از یک گره والد تشکیل شده است که می‌تواند از 0 تا 2 گره داشته باشد. این می تواند یک گره کودک چپ و/یا یک گره فرزند راست یا اصلاً بدون گره داشته باشد. در یک درخت باینری کامل، تمام گره ها پر می شوند به جز آخرین سطح که می تواند پر باشد، اما نیازی به پر بودن ندارد. آخرین سطح، سطح n، می تواند از 1 تا 2n گره داشته باشد، جایی که اولین در n = 0 است و ریشه است.
ماکس هیپ
Max heap (یا maxheap) یک درخت باینری کامل است . نکته مهم در مورد آن این است که گره والد باید مقداری بیشتر یا مساوی با گره های چپ و راست فرزند داشته باشد. اگر این مورد رعایت نشود، شما حداکثر هپ ندارید. از سوی دیگر، Min Heap برعکس است و ریشه به عنوان کوچکترین مقدار با گره های متوالی افزایش می یابد. هر گره فرزند مقداری بزرگتر یا مساوی با والد خود دارد. همچنین یک درخت باینری کامل است. نمونه ای از max heap این است: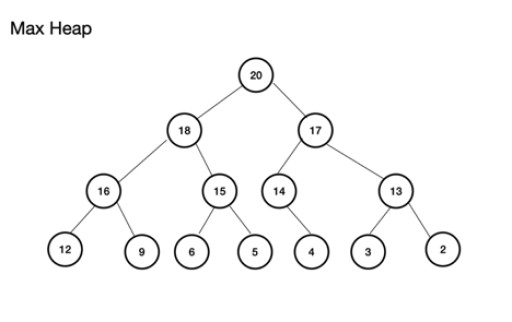
Max Heap را می توان از یک آرایه ساخت. این آرایه به صورت درختی در نظر گرفته خواهد شد. برای یک پشته، اگر ریشه، (گره والد بالای درخت) در موقعیت (شاخص) n ذخیره شود، برای آرایه، theArray ، به عنوان theArray[n] تعریف می‌شود . بنابراین گره های فرزند چپ و راست به ترتیب در Array[2n+1] و Array[2n+2] قرار دارند . برای حداکثر هیپ، ریشه در آرایه[0] است . برای سطح n، ریشه n = 0: theArr[n] گره والد است. Arr[(2*n)+1] گره فرزند سمت چپ است.
کلاس PriorityQueue
Heaps در جاوا را می توان با استفاده از کلاس PriorityQueue پیاده سازی کرد . PriorityQueues برای یافتن مهم ترین یا کم اهمیت ترین مورد در یک مجموعه استفاده می شود. کلاس PriorityQueue را می توان در java.util.package پیدا کرد . PriorityQueues باید از اشیایی تشکیل شوند که قابل مقایسه باشند به طوری که در یک ترتیب خاص در صف قرار گیرند. PriorityQueue می تواند یک مقایسه کننده داشته باشد تا مقایسه ای بین اشیا انجام شود و طبق این مقایسه صف تشکیل شود. یک مثال این است:import java.util.Comparator;
import java.util.PriorityQueue;
public class Main
{
public static void main(String[] args) {
// Create PriorityQueue with comparator for ascending order of array length
PriorityQueue intQueue = new PriorityQueue((a,b) -> a - b);
Integer [] array1 = {1, 2, 4, 6, 8, 9};
Integer [] array2 = {3, 6, 9};
Integer [] array3 = {2, 4, 8, 16, 32, 64, 128};
Integer [] array4 = {5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55};
Integer [] array5 = {4};
//Add the array lengths to intQueue
intQueue.add(array1.length);
intQueue.add(array2.length);
intQueue.add(array3.length);
intQueue.add(array4.length);
intQueue.add(array5.length);
//Write out contents of intQueue as stored
while (intQueue.size() != 0) {
System.out.println(intQueue.remove());
}
}
}
1 3 6 7 11
در این مثال، اندازه پیش فرض intQueue 11 است، بنابراین بیان نشده است (معمولاً اولین آرگومان قبل از مقایسه کننده) و مقایسه کننده به صورت زیر آورده شده است:
(a,b) -> a - b
این یک مقایسه بین آیتم های intQueue انجام می دهد و آن را به طول آرایه به ترتیب صعودی مرتب می کند.
پیاده سازی PriorityQueue برای ایجاد حداکثر هیپ
کلاس PriorityQueue به صورت پیش‌فرض روی min heap بدون مقایسه‌کننده قرار می‌گیرد. Min heap برعکس max heap است و بنابراین ریشه کوچکترین مقدار است و گره های فرزند متوالی بزرگتر یا برابر با ریشه و گره های والدین بعدی هستند. به همین دلیل، برای max heap، لازم است از reverseOrder() از چارچوب مجموعه های جاوا به عنوان مقایسه کننده استفاده شود. این اطمینان حاصل می کند که ما یک پشته حداکثر و نه حداقل هیپ را دریافت می کنیم. این کلاس متدهای مفیدی مانند add() ، contain() ، remove() ، poll() و peek() دارد .| روش | شرح | پیچیدگی زمانی |
|---|---|---|
| افزودن (J) | عنصر J را در انتهای درخت اضافه می کند | O(LogN) |
| حذف (J) | مقدار J را از درخت حذف کنید | بر) |
| نظرسنجی() | حداکثر عنصر درخت را حذف می کند | O(LogN) |
| زیرچشمی نگاه کردن() | عنصر ریشه را در بالای درخت برمی گرداند | O (1) |
| حاوی (J) | اگر J در صف باشد true، اگر نه false را برمی‌گرداند | بر) |
کد زیر نمونه ای از نحوه ایجاد max heap (maxheap) در جاوا است. اولین کاری که باید انجام دهید این است که یک آرایه را با مقادیری که max heap برای آنها ایجاد می شود پر کنید. این آرایه نامیده می شود . سپس یک PriorityQueue به نام theQueue ایجاد می شود و سپس عناصر آرایه به آن اضافه می شوند. این از متد add() استفاده می کند ، به عنوان مثال theQueue.add(10) برای اضافه کردن 10 به انتهای صف. برای نشان دادن برخی از عملکردهای کلاس PriorityQueue ، سپس از متد peek() برای یافتن سر پشته استفاده می‌شود، و این حداکثر مقدار، در این مورد، 99 است. وظیفه بعدی بررسی اندازه پشته است. با استفاده از size() که 9 است و در کنسول چاپ می شود. روش WritMaxHeap عناصر موجود در صف را به ترتیب ریشه می نویسد، فرزند چپ با ریشه به عنوان والد، فرزند راست با ریشه به عنوان والد، فرزند چپ با اولین فرزند چپ به عنوان والد، فرزند راست با اولین فرزند چپ به عنوان والد، راست فرزند با اولین فرزند راست به عنوان والد، فرزند چپ با اولین فرزند راست به عنوان والد و غیره، با مقادیر بعدی با استفاده از فرزندان چپ و راست به عنوان والدین به همان ترتیب بالا.
mport java.util.Collections;
import java.util.PriorityQueue;
public class MaxHeap {
public static void writeQueue(PriorityQueue<Integer> priorityQueue)
{
// Write out elements in queue, priorityQueue, and remove them using poll()
while(priorityQueue.size() != 0)
{
System.out.println(priorityQueue.poll());
}
}
public static void writeMaxHeap(PriorityQueue<Integer> priorityQueue)
{
// Write out elements in queue as a max heap - root, left child, right child, etc
for (Integer element : priorityQueue) {
System.out.println(element);
}
}
public static void main(String args[])
{
// Array of numbers to create a max heap array from
int[] theArray = {5, 3, 13, 10, 99, 19, 6, 51, 9};
// theQueue is created
PriorityQueue<Integer> theQueue =
new PriorityQueue<Integer>(Collections.reverseOrder());
// Elements are added to theQueue
for (int i = 0 ; i <theArray.length; ++i)
{
theQueue.add(theArray[i]);
}
// The head or root element (priority element) is printed out
System.out.println("The root value is : " + theQueue.peek());
// Find size of theQueue. Use method size()
Integer s = theQueue.size();
System.out.println("Size of theQueue? " + s);
// All elements of theQueue are printed in terms of parent,
// left child, right child
System.out.println("theQueue written using for loop:");
writeMaxHeap(theQueue);
// Does theQueue contain 10? Use method contains()
boolean b = theQueue.contains(10);
System.out.println("Does theQueue contain 10? " + b);
// Erasing value 10 from array using remove()
theQueue.remove(10);
// All elements of theQueue are printed out and removed.
// Each one is the maximum value left in the queue.
// At the end theQueue will be empty
System.out.println("theQueue written out using poll():");
writeQueue(theQueue);
// Find size of theQueue. Use method size()
s = theQueue.size();
System.out.println("Size of theQueue? " + s);
}
}
مقدار ریشه این است: 99 Size of theQueue? 9 theQueue با استفاده از حلقه 99 51 19 13 10 5 6 3 9 نوشته شده است آیا theQueue شامل 10 است؟ true theQueue با استفاده از poll() نوشته شده است 99 51 19 13 9 6 5 3 Size of theQueue؟ 0
مکس هیپیفای
الگوریتم Max Heapify برای اطمینان از اینکه یک درخت باینری یک max heap است استفاده می شود. اگر ما در یک گره، n، و گره های فرزند آن، چپ و راست نیز خود max heap هستند، پس عالی است، ما یک max heap داریم. اگر در سرتاسر درخت اینطور نباشد، ما حداکثر هیپ نداریم. الگوریتم Max Heapify برای مرتب‌سازی درخت به‌گونه‌ای استفاده می‌شود که به اصول maxheap پایبند باشد. Max Heapify فقط روی یک گره کار می کند. اگر شرط این است که آرایه یک آرایه max heap باشد، پس همه درختان فرعی باید قبل از ریشه به maxheap تبدیل شوند، هر بار. الگوریتم باید در هر گره استفاده شود. این کار روی گره های N/2 انجام می شود (برگ ها به حداکثر الزامات پشته پایبند هستند). پیچیدگی زمانی پشته O(NlogN) و برای یک گره در ارتفاع X، پیچیدگی زمانی O(X) است. کد زیر نحوه maxheapify یک درخت (آرایه) را نشان می دهد.public class MaxHeapify
{
public static Integer[] maxHeapify(Integer[ ] array, Integer i)
{
// Create left-child and right-child for the node in question
Integer leftChild = 2 * i + 1;
Integer rightChild = 2 * i + 2;
// Assign maxVal to parent node, i
Integer maxVal = i;
// Set maxVal to greater of the two: node or left-child
if( leftChild < array.length && array[leftChild] > array[maxVal] )
maxVal = leftChild;
// Set maxVal to greater of the two: maxVal or right-child
if( rightChild < array.length && array[rightChild] > array[maxVal] )
maxVal = rightChild;
// Check if maxVal is not equal to parent node, then set parent node to
// maxVal, swap values and then do a maxheapify on maxVal
// which is now the previous parent node
if( maxVal != i )
{
Integer value = array[i];
array[i] = array[maxVal];
array[maxVal] = value;
array = maxHeapify(array, maxVal);
}
return array;
}
public static Integer[] maxHeapCreate(Integer array[])
{
// Call maxHeapify to arrange array in a max heap
Integer [] theNewArr = array;
for( Integer i = array.length/2; i >= 0; i-- )
theNewArr = maxHeapify(array, i);
return theNewArr;
}
public static void main(String[] args)
{
// Create array to be maxheapified, theArray,
// and array, newArray, to write results into, by calling maxheapCreate
// newArray will now be a maxheap
Integer[] theArray = {5, 3, 13, 10, 99, 19, 6, 51, 9};
Integer[ ] newArray = maxHeapCreate(theArray);
// Print out contents of newArray
System.out.println("newArray:");
for(int i = 0; i < newArray.length; ++i)
{
System.out.println(newArray[i]);
}
// Print out labelled contents of newArray
System.out.println(" root : " + newArray[0]);
for (int i = 0; i <= newArray.length/2 - 1; i++) {
System.out.print(" parent node : " + newArray[i] + " left child : " +
newArray[(2*i)+1] + " right child :" + newArray[(2*i)+2]);
System.out.println();
}
}
}
newArray: 99 51 19 10 3 13 6 5 9 ريشه : 99 گره والد : 99 فرزند چپ : 51 فرزند راست :19 گره والد : 51 فرزند چپ : 10 فرزند راست : 3 گره والد : 19 فرزند چپ : 13 فرزند راست : گره والد : 10 فرزند چپ : 5 فرزند راست : 9
در این کد آرایه ایجاد شده و با اعداد پر می شود. آرایه دوم به نام newArray ایجاد می شود و این بار حاوی نتیجه متد maxheapCreate ، آرایه max heap خواهد بود. روش maxHeapCreate از main فراخوانی می شود و در اینجا یک آرایه جدید به نام theNewArr ایجاد می شود و با نتایج maxHeapify پر می شود . این کار با حلقه کردن بیش از نیمی از اندازه آرایه ورودی انجام می شود. برای هر پاس حلقه، متد maxHeapify نامیده می شود که از عنصری در وسط آرایه شروع می شود و به عنصر اول ختم می شود. برای هر فراخوانی maxHeapify ، فرزند سمت چپ و فرزند سمت راست گره والد، i، پیدا می‌شوند و بررسی می‌شود که کدام یک از این سه مورد بزرگترین است، و آن را به عنوان maxVal تعریف می‌کنیم . اگر maxVal برابر با گره والد نباشد، یک مبادله انجام می شود تا گره والد و maxVal مبادله شوند و سپس maxHeapify این بار دوباره در maxVal فراخوانی می شود و همان مراحل قبلی انجام می شود. در نهایت حداکثر پشته ایجاد خواهد شد و دیگر تکراری برای انجام وجود نخواهد داشت. آرایه به روز شده، آرایه ، اکنون به عنوان newArray به اصلی بازگردانده می شود و سپس هر عنصر متوالی در کنسول چاپ می شود. newArray اکنون یک max heap است. توجه داشته باشید که مانند مثال قبلی با استفاده از PriorityQueue اعداد نوشته می شوند: ریشه، فرزند راست ریشه به عنوان والد، فرزند سمت چپ ریشه به عنوان والد، فرزند راست فرزند اول راست فرزند به عنوان والد، فرزند سمت چپ از ریشه چپ‌فرزند به‌عنوان والد، راست‌فرزند اول چپ‌فرزند به‌عنوان والد، چپ‌فرزند اول راست فرزند به‌عنوان والد، و غیره. ترتیبی کمی با ترتیب استفاده از PriorityQueue دارند، زیرا مقایسه بین عناصر متوالی انجام می‌شود . در حالی که در مثال maxheapify، گره با دو عنصر متوالی بعدی در آرایه مقایسه شده و با بزرگترین مقدار مبادله می شود. به طور خلاصه، از دو الگوریتم مختلف استفاده می شود. هر دو یک پشته حداکثر ایجاد می کنند.
GO TO FULL VERSION