پرسش و پاسخ از مصاحبه های شغلی: الگوریتم ها در جاوا، بخش 2

این قسمت دوم از مروری کوتاه بر الگوریتم ها است. در اینجا پیوندی به مقاله اول وجود دارد . قبلاً الگوریتم‌های مختلفی را برای مرتب‌سازی آرایه‌ها و همچنین به اصطلاح الگوریتم حریص بررسی کردیم. امروز در مورد نمودارها و الگوریتم های مرتبط با آنها صحبت خواهیم کرد. گراف یکی از انعطاف پذیرترین و همه کاره ترین ساختارها در برنامه نویسی است. نمودار G معمولاً با یک جفت مجموعه تعریف می شود، یعنی G = (V, R)، که در آن:

• V مجموعه ای از رئوس است.
• R مجموعه ای از خطوط است که جفت رئوس را به هم متصل می کند.

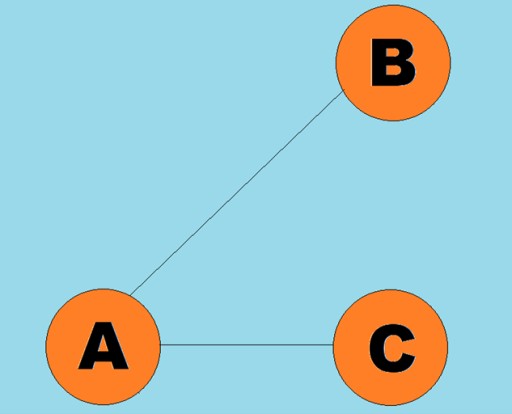خطوط اتصال بدون جهت را لبه می نامند: خطوط جهت دار را قوس می گویند: 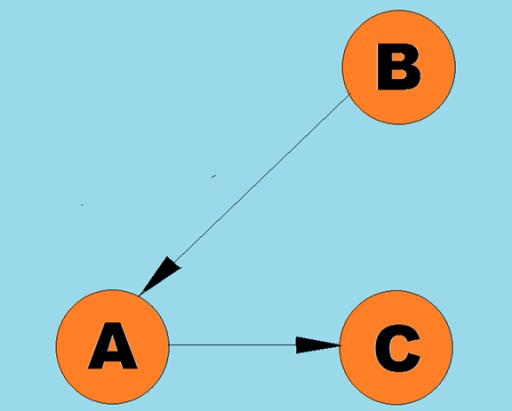به طور معمول، یک نمودار با نموداری نشان داده می شود که در آن برخی از رئوس توسط یال ها (قوس) به هم متصل می شوند. نمودارهایی که لبه های آنها جهت پیمایش را نشان می دهد، گراف های جهت دار نامیده می شوند. اگر یک نمودار توسط یال هایی به هم متصل شود که جهت پیمایش را نشان نمی دهند، می گوییم یک گراف بدون جهت است. این بدان معنی است که حرکت در هر دو جهت امکان پذیر است: هم از راس A به راس B، و هم از راس B به راس A. گراف متصل، نموداری است که در آن حداقل یک مسیر از هر راس به هر راس دیگری منتهی می شود (مانند راس مثال بالا). اگر اینطور نباشد، می گویند نمودار قطع شده است: 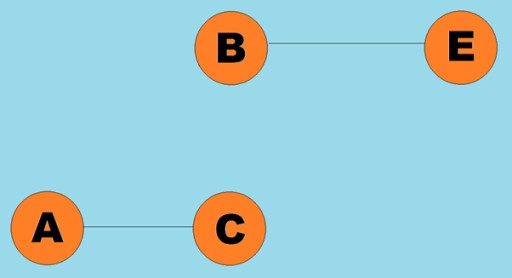وزن ها را نیز می توان به یال ها (قوس ها) اختصاص داد. وزن ها اعدادی هستند که به عنوان مثال، فاصله فیزیکی بین دو راس (یا زمان نسبی سفر بین دو راس) را نشان می دهند. به این نمودارها نمودارهای وزنی می گویند: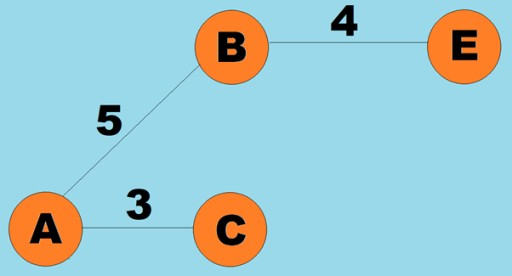

3. الگوریتم های مسیریابی (اول عمق، اول عرض)

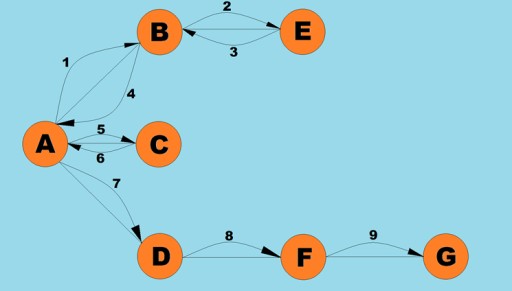
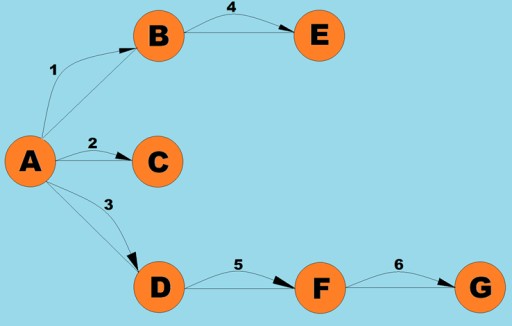
یکی از عملیات اساسی که با نمودارها انجام می شود، تعیین تمام رئوس قابل دستیابی از یک راس معین است. تصور کنید که سعی دارید تعیین کنید که چگونه می توانید از شهری به شهر دیگر سوار اتوبوس شوید، از جمله نقل و انتقالات احتمالی. دسترسی به برخی شهرها به طور مستقیم امکان پذیر است، در حالی که دسترسی به برخی از شهرها تنها با عبور از شهرهای دیگر امکان پذیر است. موقعیت های بسیار دیگری وجود دارد که ممکن است لازم باشد تمام رئوسی را که می توانید از یک راس مشخص به آن برسید پیدا کنید. دو راه اصلی برای پیمایش نمودارها وجود دارد: ابتدا عمق و اول عرض. ما هر دوی اینها را بررسی خواهیم کرد. هر دو روش تمام رئوس متصل را طی می کنند. برای بررسی بیشتر الگوریتم‌های عمق اول و عرض اول، از نمودار زیر استفاده می‌کنیم:

جستجوی عمقی

این یکی از رایج ترین روش های پیمایش نمودار است. اولین استراتژی عمق این است که تا جایی که ممکن است در یک نمودار عمیق بروید. سپس پس از رسیدن به بن بست، به نزدیکترین راس که قبلاً رئوس مجاور دیده نشده است، برمی گردیم. این الگوریتم اطلاعاتی را در پشته ذخیره می کند که در صورت رسیدن به بن بست کجا باید برگردند. قوانین جستجوی عمقی:

1. از یک راس مجاور که قبلاً بازدید نشده بود دیدن کنید، آن را به عنوان بازدید شده علامت گذاری کنید و آن را روی پشته فشار دهید.
2. به این راس حرکت کنید.
3. مرحله 1 را تکرار کنید.
4. اگر مرحله 1 غیرممکن است، به راس قبلی برگردید و سعی کنید مرحله 1 را انجام دهید. اگر این امکان وجود نداشت، به راس قبل از آن یکی برگردید و به همین ترتیب ادامه دهید تا زمانی که یک راس پیدا کنیم که بتوانیم پیمایش را از آن ادامه دهیم.
5. ادامه دهید تا تمام رئوس روی پشته قرار گیرند.

بیایید نگاهی بیندازیم که کد جاوا برای این الگوریتم ممکن است به چه شکل باشد:

public class Graph {
  private final int MAX_VERTS = 10;
  private Vertex vertexArray[]; // Array of vertices
  private int adjMat[][]; // Adjacency matrix
  private int nVerts; // Current number of vertices
  private Stack stack;

  public Graph() { // Initialize internal fields
     vertexArray = new Vertex[MAX_VERTS];
     adjMat = new int[MAX_VERTS][MAX_VERTS];
     nVerts = 0;
     for (int j = 0; j < MAX_VERTS; j++) {
        for (int k = 0; k < MAX_VERTS; k++) {
           adjMat[j][k] = 0;
        }
     }
     stack = new Stack<>();
  }

  public void addVertex(char lab) {
     vertexArray[nVerts++] = new Vertex(lab);
  }

  public void addEdge(int start, int end) {
     adjMat[start][end] = 1;
     adjMat[end][start] = 1;
  }

  public void displayVertex(int v) {
     System.out.println(vertexArray[v].getLabel());
  }

  public void dfs() { // Depth-first search
     vertexArray[0].setVisited(true); // Take the first vertex
     displayVertex(0);
     stack.push(0);

     while (!stack.empty()) {
        int v = getAdjUnvisitedVertex(stack.peek()); // Return the index of the adjacent vertex: if any, 1; if not, -1
        if (v == -1) { // If there is no unvisited adjacent vertex
           stack.pop(); // The element is removed from the stack
        }
        else {
           vertexArray[v].setVisited(true);
           displayVertex(v);
           stack.push(v); // The element goes on top of the stack
        }
     }

     for (int j = 0; j < nVerts; j++) {  // Reset the flags
        vertexArray[j].visited = false;
     }

  }

  private int getAdjUnvisitedVertex(int v) {
     for (int j = 0; j < nVerts; j++) {
        if (adjMat[v][j] == 1 && vertexArray[j].visited == false) {
           return j; // Returns the first vertex found
        }
     }
     return -1;
  }
}

یک راس به شکل زیر است:

public class Vertex {
  private char label;  // for example, 'A'
  public boolean visited;

  public Vertex(final char label) {
     this.label = label;
     visited = false;
  }

  public char getLabel() {
     return this.label;
  }

  public boolean isVisited() {
     return this.visited;
  }

  public void setVisited(final boolean visited) {
     this.visited = visited;
  }
}

بیایید این الگوریتم را با رئوس مشخص اجرا کنیم و ببینیم که آیا درست کار می کند یا خیر:

public class Solution {
  public static void main(String[] args) {
     Graph graph = new Graph();
     graph.addVertex('A'); //0
     graph.addVertex('B'); //1
     graph.addVertex('C'); //2
     graph.addVertex('D'); //3
     graph.addVertex('E'); //4
     graph.addVertex('F'); //5
     graph.addVertex('G'); //6

     graph.addEdge(0,1);
     graph.addEdge(0,2);
     graph.addEdge(0,3);
     graph.addEdge(1,4);
     graph.addEdge(3,5);
     graph.addEdge(5,6);

     System.out.println("Visits: ");
     graph.dfs();
  }
}

خروجی کنسول: از آنجایی که ما یک ماتریس مجاورت داریم و از یک حلقه در یک حلقه استفاده می کنیم، پیچیدگی زمانی O(N²) خواهد بود.

جستجوی اول عرض

این الگوریتم مانند جستجوی عمق، یکی از ساده ترین و اساسی ترین روش های پیمایش نمودار است. خلاصه این است که ما مقداری راس فعلی داریم. تمام رئوس مجاور بازدید نشده آن را در یک صف قرار می دهیم و عنصر بعدی (که راس ذخیره شده در سر صف است) را انتخاب می کنیم که تبدیل به راس فعلی می شود... با تقسیم این الگوریتم به مراحل، می توانیم مراحل زیر را شناسایی کنیم:

1. از رأس بعدی که قبلاً بازدید نشده است در مجاورت راس فعلی بازدید کنید، آن را به عنوان بازدید شده از قبل علامت گذاری کنید و آن را به صف اضافه کنید.
2. اگر مرحله 1 را نمی توان انجام داد، راس را از صف حذف کنید و آن را به راس فعلی تبدیل کنید.
3. اگر مراحل #1 و #2 را نتوان انجام داد، در این صورت ما پیمایش را تمام کرده ایم - هر رأس پیمایش شده است (اگر یک گراف متصل داشته باشیم).

کلاس گراف در اینجا تقریباً مشابه کلاسی است که ما برای الگوریتم جستجوی عمق اول استفاده کردیم، به جز خود روش جستجو و این واقعیت که یک صف جایگزین پشته داخلی می شود:

public class Graph {
  private final int MAX_VERTS = 10;
  private Vertex vertexList[]; // Array of vertices
  private int adjMat[][]; // Adjacency matrix
  private int nVerts; // Current number of vertices
  private Queue queue;

  public Graph() {
     vertexList = new Vertex[MAX_VERTS];
     adjMat = new int[MAX_VERTS][MAX_VERTS];
     nVerts = 0;
     for (int j = 0; j < MAX_VERTS; j++) {
        for (int k = 0; k < MAX_VERTS; k++) {  // Fill the adjacency matrix with zeros
           adjMat[j][k] = 0;
        }
     }
     queue = new PriorityQueue<>();
  }

  public void addVertex(char lab) {
     vertexList[nVerts++] = new Vertex(lab);
  }

  public void addEdge(int start, int end) {
     adjMat[start][end] = 1;
     adjMat[end][start] = 1;
  }

  public void displayVertex(int v) {
     System.out.println(vertexList[v].getLabel());
  }

  public void bfc() { // Depth-first search
     vertexList[0].setVisited(true);
     displayVertex(0);
     queue.add(0);
     int v2;

     while (!queue.isEmpty()) {
        int v = queue.remove();

        while((v2 = getAdjUnvisitedVertex(v))!=-1) {// The loop runs until every adjacent vertex is found and added to the queue
           vertexList[v2].visited = true;
           displayVertex(v2);
           queue.add(v2);
        }
     }

     for (int j = 0; j < nVerts; j++) {  // Reset the flags
        vertexList[j].visited = false;
     }

  }

  private int getAdjUnvisitedVertex(int v) {
     for (int j = 0; j < nVerts; j++) {
        if (adjMat[v][j] == 1 && vertexList[j].visited == false) {
           return j; // Returns the first vertext found
        }
     }
     return -1;
  }
}

کلاس Vertex با کلاسی که در الگوریتم جستجوی عمق اول استفاده کردیم یکسان است. بیایید این الگوریتم را عملی کنیم:

public class Solution {
  public static void main(String[] args) {
     Graph graph = new Graph();
     graph.addVertex('A'); //0
     graph.addVertex('B'); //1
     graph.addVertex('C'); //2
     graph.addVertex('D'); //3
     graph.addVertex('E'); //4
     graph.addVertex('F'); //5
     graph.addVertex('G'); //6

     graph.addEdge(0,1);
     graph.addEdge(0,2);
     graph.addEdge(0,3);
     graph.addEdge(1,4);
     graph.addEdge(3,5);
     graph.addEdge(5,6);

     System.out.println("Visits: ");
     graph.bfc();
  }
}

خروجی کنسول: باز هم: ما یک ماتریس مجاورت داریم و از یک حلقه تو در تو در یک حلقه استفاده می کنیم، بنابراین پیچیدگی زمانی الگوریتم فوق O(N²) است.

4. الگوریتم دایکسترا

همانطور که قبلا ذکر شد، نمودارها می توانند جهت دار یا بدون جهت باشند. و به یاد خواهید آورد که آنها را نیز می توان وزن کرد. نمودارهای وزن دار و جهت دار مدل روابط اغلب در زندگی واقعی یافت می شوند: به عنوان مثال، نقشه شهرهایی که در آن شهرها راس هستند، و یال های بین آنها جاده هایی با ترافیک یک طرفه هستند که در جهت یال هدایت شده جریان دارند. فرض کنید شما یک شرکت باربری هستید و باید کوتاه ترین مسیر را بین دو شهر دوردست پیدا کنید. چگونه آن را انجام می دهید؟ یافتن کوتاه ترین مسیر بین دو راس یکی از رایج ترین مسائلی است که با استفاده از نمودارهای وزنی حل می شود. برای حل این مشکل از الگوریتم Dijkstra استفاده می کنیم. هنگامی که آن را اجرا کنید، کوتاه ترین مسیرها را از یک راس اولیه معین به هر یک دیگر خواهید دانست. مراحل این الگوریتم چیست؟ من سعی خواهم کرد به این سوال پاسخ دهم. مراحل الگوریتم دایکسترا:

• مرحله 1: گره مجاوری را پیدا کنید که کمترین هزینه را برای پیمایش دارد (کمترین وزن لبه). شما در همان ابتدا ایستاده اید و به این فکر می کنید که به کجا بروید: به گره A یا گره B. هزینه انتقال به هر یک از این گره ها چقدر است؟
• مرحله 2: محاسبه مسافت طی شده تا همه همسایگان گره В که هنوز توسط الگوریتم هنگام عبور از لبه از В مشاهده نشده است. اگر فاصله جدید کمتر از فاصله قبلی باشد، مسیر عبور از لبه B به کوتاه ترین مسیر جدید برای این راس تبدیل می شود.
• مرحله 3: راس B را به عنوان بازدید شده علامت گذاری کنید.
• مرحله 4: به مرحله 1 بروید.

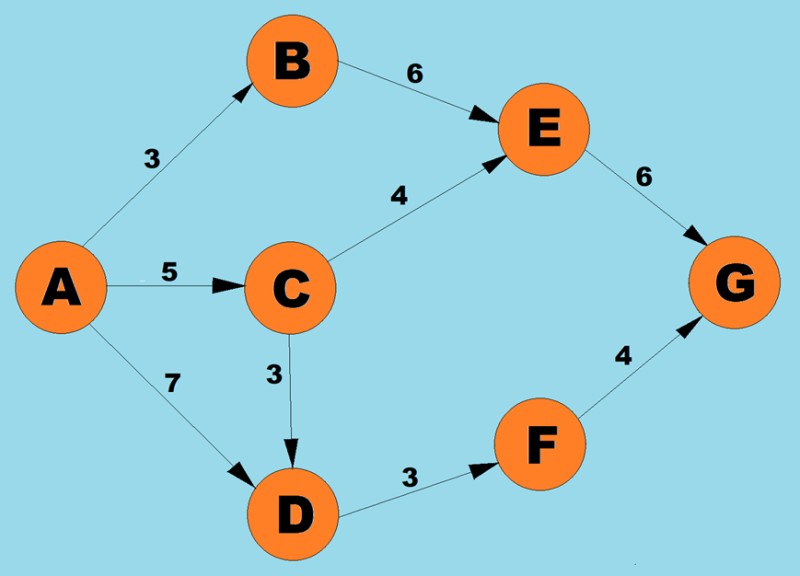ما این مراحل را در یک حلقه تکرار می کنیم تا زمانی که تمام راس ها بازدید شوند. بیایید نمودار وزنی جهت دار زیر را در نظر بگیریم: با استفاده از الگوریتم بالا، کوتاه ترین مسیر A تا G را تعیین می کنیم:

1. سه مسیر ممکن برای راس A وجود دارد: به B با وزن 3، به C با وزن 5 و به D با وزن 7. طبق مرحله اول الگوریتم، گره با کمترین هزینه (وزن لبه) را انتخاب می کنیم. در این مورد، B.

2. از آنجایی که تنها همسایه بازدید نشده B، راس E است، بررسی می کنیم که اگر از این راس عبور کنیم، مسیر چگونه خواهد بود. 3 (AB) + 6 (BE) = 9.

   بنابراین، ثبت می کنیم که کوتاه ترین مسیر فعلی از A به E 9 است.

3. از آنجایی که کار ما با راس B کامل شده است، به انتخاب راس بعدی که لبه آن حداقل وزن را دارد، می پردازیم.

   از رئوس A و B، احتمالات رئوس D (7)، C (5)، یا E (6) هستند.

   لبه تا С کمترین وزن را دارد، بنابراین به این راس می رویم.

4. در مرحله بعد، مانند قبل، کوتاه ترین مسیر را به رئوس همسایه هنگام عبور از C پیدا می کنیم:

   • AD = 5 (AC) + 3 (CD) = 8، اما از آنجایی که کوتاهترین مسیر قبلی (AC = 7) کمتر از این مسیر از طریق C است، ما کوتاهترین مسیر (AC = 7) را بدون تغییر نگه میداریم.

   • CE = 5(AC) + 4(CE) = 9. این کوتاه ترین مسیر جدید برابر با مسیر قبلی است، بنابراین ما نیز آن را بدون تغییر رها می کنیم.

5. از نزدیکترین رئوس قابل دسترس (E و D)، راس با کوچکترین وزن لبه، یعنی D (3) را انتخاب کنید.

6. ما کوتاه ترین مسیر را به همسایه اش F پیدا می کنیم.

   AF = 7 (AD) + 3 (DF) = 9

7. از نزدیکترین رئوس قابل دسترس (E و F)، راس با کوچکترین وزن لبه، یعنی F (3) را انتخاب کنید.

8. کوتاه ترین مسیر به همسایه G را پیدا کنید.

   AG = 7 (AD) + 3 (DF) + 4 (FG) = 14

   بنابراین، ما مسیری از A به G پیدا کرده ایم.

   اما برای اطمینان از کوتاه ترین آن، باید مراحل خود را روی راس E نیز انجام دهیم.

9. از آنجایی که راس G هیچ راس همسایه‌ای ندارد که با یال‌های جهت‌دار به آن اشاره شده باشد، فقط راس E باقی مانده است، بنابراین آن را انتخاب می‌کنیم.

10. کوتاه ترین مسیر به همسایه G را پیدا کنید.

    AG = 3 (AB) + 6 (BE) + 6 (EG) = 15. این مسیر از کوتاه ترین مسیر قبلی (AG (14)) طولانی تر است، بنابراین این مسیر را بدون تغییر رها می کنیم.

    از آنجایی که هیچ راسی منتهی به G وجود ندارد، اجرای مراحل روی الگوریتم روی این راس منطقی نیست. یعنی کار الگوریتم کامل شده است.

همانطور که قبلاً گفتم، ما علاوه بر یافتن کوتاه‌ترین مسیر برای AG، کوتاه‌ترین مسیرها را از راس A به هر راس دیگر (AB، AC، AD، AE، AF) نیز به دست آوردیم. خوب، اکنون زمان آن رسیده است که نگاهی به نحوه انجام این کار در جاوا بیندازیم. بیایید با کلاس رأس شروع کنیم:

public class Vertex {
   private char label;
   private boolean isInTree;

   public Vertex(char label) {
       this.label = label;
       this.isInTree = false;
   }

   public char getLabel() {
       return label;
   }

   public void setLabel(char label) {
       this.label = label;
   }

   public boolean isInTree() {
       return isInTree;
   }

   public void setInTree(boolean inTree) {
       isInTree = inTree;
   }
}

کلاس رأس تقریباً با کلاس رأس مورد استفاده برای جستجوی عرضی یکسان است. برای نمایش کوتاه ترین مسیرها، به یک کلاس جدید نیاز داریم که حاوی داده های مورد نیاز ما باشد:

public class Path { // A class that contains the distance and the previous and traversed vertices
   private int distance; // Current distance from the starting vertex
   private List parentVertices; // Current parent vertex

   public Path(int distance) {
       this.distance = distance;
       this.parentVertices = new ArrayList<>();
   }

   public int getDistance() {
       return distance;
   }

   public void setDistance(int distance) {
       this.distance = distance;
   }

   public List getParentVertices() {
       return parentVertices;
   }

   public void setParentVertices(List parentVertices) {
       this.parentVertices = parentVertices;
   }
}

در این کلاس می‌توان فاصله کل مسیر و رئوس‌هایی را که هنگام عبور از کوتاه‌ترین مسیر طی می‌شوند، مشاهده کرد. و حالا بیایید به کلاسی نگاه کنیم که در واقع کوتاه ترین مسیر را در نمودار طی می کنیم. بنابراین در اینجا ما کلاس Graph را داریم:

public class Graph {
   private final int MAX_VERTS = 10;// Maximum number of vertices
   private final int INFINITY = 100000000; // This number represents infinity
   private Vertex vertexList[]; // List of vertices
   private int relationMatrix[][]; // Matrix of edges between vertices
   private int numberOfVertices; // Current number of vertices
   private int numberOfVerticesInTree; // Number of visited vertices in the tree
   private List shortestPaths; // List of shortest paths
   private int currentVertex; // Current vertex
   private int startToCurrent; // Distance to currentVertex

   public Graph() {
       vertexList = new Vertex[MAX_VERTS]; // Adjacency matrix
       relationMatrix = new int[MAX_VERTS][MAX_VERTS];
       numberOfVertices = 0;
       numberOfVerticesInTree = 0;
       for (int i = 0; i < MAX_VERTS; i++) { // Fill the adjacency matrix
           for (int k = 0; k < MAX_VERTS; k++) { // with "infinity"
               relationMatrix[i][k] = INFINITY; // Assign default values
               shortestPaths = new ArrayList<>(); // Assign an empty list
           }
       }
   }

   public void addVertex(char lab) {// Assign new vertices
       vertexList[numberOfVertices++] = new Vertex(lab);
   }

   public void addEdge(int start, int end, int weight) {
       relationMatrix[start][end] = weight; // Set weighted edges between vertices
   }

   public void path() { // Choose the shortest path
       // Set the initial vertex data
       int startTree = 0; // Start from vertex 0
       vertexList[startTree].setInTree(true); // Include the first element in the tree
       numberOfVerticesInTree = 1;

       // Fill out the shortest paths for vertices adjacent to the initial vertex
       for (int i = 0; i < numberOfVertices; i++) {
           int tempDist = relationMatrix[startTree][i];
           Path path = new Path(tempDist);
           path.getParentVertices().add(0);// The starting vertex will always be a parent vertex
           shortestPaths.add(path);
       }
       // Until every vertex is in the tree
       while (numberOfVerticesInTree < numberOfVertices) { // Do this until the number of of vertices in the tree equals the total number of vertices
           int indexMin = getMin();// Get the index of the of the vertex with the smallest distance from the vertices not yet in the tree
           int minDist = shortestPaths.get(indexMin).getDistance(); // Minimum distance to the vertices not yet in the tree

           if (minDist == INFINITY) {
               System.out.println("The graph has an unreachable vertex");
               break; // If only unreachable vertices have not been visited, then we exit the loop
           } else {
               currentVertex = indexMin; // Set currentVert to the index of the current vertex
               startToCurrent = shortestPaths.get(indexMin).getDistance(); // Set the distance to the current vertex
           }

           vertexList[currentVertex].setInTree(true);  // Add the current vertex to the tree
           numberOfVerticesInTree++; // Increase the count of vertices in the tree
           updateShortestPaths(); // Update the list of shortest paths
       }

       displayPaths(); // Display the results on the console
   }

   public void clear() { // Clear the tree
       numberOfVerticesInTree = 0;
       for (int i = 0; i < numberOfVertices; i++) {
           vertexList[i].setInTree(false);
       }
   }

   private int getMin() {
       int minDist = INFINITY; // The distance of the initial shortest path is taken to be infinite
       int indexMin = 0;
       for (int i = 1; i < numberOfVertices; i++) { // For each vertex
           if (!vertexList[i].isInTree() && shortestPaths.get(i).getDistance() < minDist) { // If the vertex is not yet in the tree and the distance to the vertex is less than the current minimum
               minDist = shortestPaths.get(i).getDistance(); // then update the minimum
               indexMin = i; // Update the index of the vertex with the minimum distance
           }
       }
       return indexMin; // Returns the index of the vertex with the smallest distance among those not yet in the tree
   }

   private void updateShortestPaths() {
       int vertexIndex = 1; // The initial vertex is skipped
       while (vertexIndex < numberOfVertices) { // Run over the columns

           if (vertexList[vertexIndex].isInTree()) { // If the column vertex is already in the tree, then we skip it
               vertexIndex++;
               continue;
           }
           // Calculate the distance for one element sPath
           // Get the edge from currentVert to column
           int currentToFringe = relationMatrix[currentVertex][vertexIndex];
           // Add up all the distances
           int startToFringe = startToCurrent + currentToFringe;
           // Determine the distance to the current vertexIndex
           int shortPathDistance = shortestPaths.get(vertexIndex).getDistance();

           // Compare the distance through currentVertex with the current distance in the vertex with index vertexIndex
           if (startToFringe < shortPathDistance) { // If it is smaller, then the vertex at vertexIndex is assigned the new shortest path
               List newParents = new ArrayList<>(shortestPaths.get(currentVertex).getParentVertices()); // Create a copy of the list of vertices of vertex currentVert's parents
               newParents.add(currentVertex); // And add currentVertex to it as the previous vertex
               shortestPaths.get(vertexIndex).setParentVertices(newParents); // Save the new path
               shortestPaths.get(vertexIndex).setDistance(startToFringe); // Save the new distance
           }
           vertexIndex++;
       }
   }

   private void displayPaths() { // A method for displaying the shortest paths on the screen
       for (int i = 0; i < numberOfVertices; i++) {
           System.out.print(vertexList[i].getLabel() + " = ");
           if (shortestPaths.get(i).getDistance() == INFINITY) {
               System.out.println("0");
           } else {
               String result = shortestPaths.get(i).getDistance() + " (";
               List parents = shortestPaths.get(i).getParentVertices();
               for (int j = 0; j < parents.size(); j++) {
                   result += vertexList[parents.get(j)].getLabel() + " -> ";
               }
               System.out.println(result + vertexList[i].getLabel() + ")");
           }
       }
   }
}

پس این همه جادو است =) حالا بیایید نگاهی به این الگوریتم در عمل بیندازیم:

public class Solution {

   public static void main(String[] args) {
       Graph graph = new Graph();
       graph.addVertex('A');
       graph.addVertex('B');
       graph.addVertex('C');
       graph.addVertex('D');
       graph.addVertex('E');
       graph.addVertex('F');
       graph.addVertex('G');

       graph.addEdge(0, 1, 3);
       graph.addEdge(0, 2, 5);
       graph.addEdge(0, 3, 7);
       graph.addEdge(1, 4, 6);
       graph.addEdge(2, 4, 4);
       graph.addEdge(2, 3, 3);
       graph.addEdge(3, 5, 3);
       graph.addEdge(4, 6, 6);
       graph.addEdge(5, 6, 4);

       System.out.println("The following nodes form the shortest paths from node A:");
       graph.path();
       graph.clear();
   }
}

و خروجی کنسول این است: پیچیدگی زمانی این الگوریتم چیزی جز O(N²) نیست، زیرا ما حلقه های تودرتو داریم. این تمام چیزی است که امروز دارم. از توجه شما ممنونم!