Java מיון בועות

אם שמעתם פעם על שיטות מיון בתכנות, סביר להניח שזה היה אלגוריתם מיון הבועות. זה מפורסם. כל מתכנת מכיר את מיון הבועות (או לפחות שמע עליו תוך כדי למידה) לא בגלל שזהו אלגוריתם המיון הטוב בעולם, אלא הכי קל. אלגוריתם זה משמש בדרך כלל למטרות למידה או שאתה עשוי לקבל אותו כמשימה בראיון Java Junior שלך. קל מאוד להבין אלגוריתם מיון בועות Java, אולם הוא אינו יעיל. בכל מקרה, בוא נבין את זה.

מה זה מיון

קודם כל, אתה צריך להבין מהו מיון באופן כללי ומה אנחנו יכולים למיין בתוכנות Java. אם נוכל להשוות שני אלמנטים או אובייקטים או יותר לפי כל אחת מהתכונות שלהם, זה אומר שניתן למיין אותם לפי תכונה זו. לדוגמה, מספרים בסדר עולה או יורד או מילים בסדר אלפביתי. לפיכך, האלמנטים חייבים להיות ניתנים להשוואה זה עם זה. אגב, המרכיבים של מה? ב-Java, אנו יכולים להשוות את האלמנטים של Collections. לדוגמה, אנו יכולים למיין Array או ArrayList של מספרים שלמים, מחרוזות וכן הלאה.

איך מיון בועות עובד

נניח, עלינו למיין מערך של מספרים שלמים בסדר עולה, כלומר מהמספר הקטן ביותר למספר הגדול ביותר. ראשית, אנו הולכים לאורך כל המערך ומשווים כל 2 אלמנטים שכנים. אם הם בסדר הלא נכון (השכן השמאלי גדול יותר מהימין), אנחנו מחליפים אותם. במעבר הראשון בסוף הוא יופיע האלמנט הגדול ביותר (אם נמיין בסדר עולה). אתה יכול לומר, האלמנט הגדול ביותר "צץ". זו הסיבה לשם אלגוריתם מיון בועה. אנו חוזרים על השלב הראשון מהאלמנט הראשון לאלמנט הבא לאחרון. יש לנו את האלמנט השני בגודלו במקום הבא אחרון. וכולי. אנחנו יכולים לשפר מעט אלגוריתם עם בדיקה אם בוצעה לפחות החלפה אחת בשלב הקודם. אם לא, אנחנו עוצרים את הריצה שלנו לאורך המערך.

דוגמה למיון בועות

בוא נמיין את מערך המספרים השלמים, האחד, שאתה עשוי לראות למטה בתמונה. שלב 1: אנחנו עוברים על המערך. האלגוריתם מתחיל בשני האלמנטים הראשונים (עם המדדים 0 ו-1), 8 ו-7, ובודק אם הם בסדר הנכון. ברור, 8 > 7, אז אנחנו מחליפים אותם. לאחר מכן, אנו מסתכלים על האלמנטים השני והשלישי (מדדים 1 ו-2), כעת אלו הם 8 ו-1. מאותן סיבות, אנו מחליפים אותם. בפעם השלישית אנחנו משווים 8 ו-2 ולפחות 8 ו-5. ביצענו ארבע החלפות בסך הכל: (8, 7), (8, 1), (8, 2) ו- (8, 5). ערך של 8, הגדול ביותר במערך הזה, צץ בסוף הרשימה למיקום הנכון. 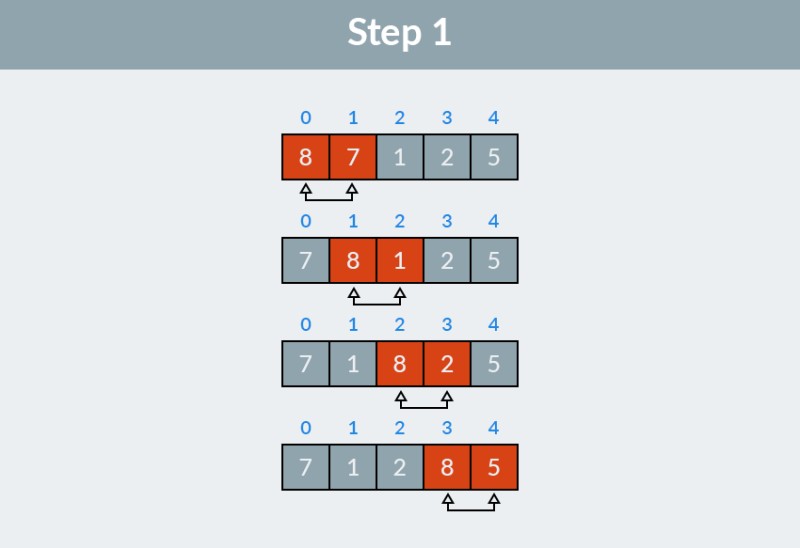התוצאה של השלב הראשון של אלגוריתם מיון בועה היא המערך הבא: שלב 2. עושים את אותו הדבר עם (7,1), (7,2) ו-(7,5). 7 נמצא כעת במיקום הלפני אחרון, ואנחנו לא צריכים להשוות אותו ל"זנב" של הרשימה, הוא כבר ממוין. התוצאה של השלב השני של אלגוריתם מיון בועה הפועלת היא המערך הבא: כפי שאתה עשוי לראות, המערך הזה כבר ממוין. בכל מקרה אלגוריתם מיון בועה אמור להתחיל לעבוד לפחות פעם נוספת. שלב 3. אנחנו עוברים על המערך פעם נוספת. אין מה להחליף כאן, אז אם אנחנו משתמשים באלגוריתם מיון בועות "משופר" (עם בדיקה אם בוצעה לפחות החלפה אחת בשלב הקודם) השלב הזה הוא האחרון.

קוד Java מיון בועות

מימוש Java מיון בועות

בואו ניצור שתי שיטות למיון בועה. הראשון, bubbleSort(int[] myArray) הוא מישורי. זה עובר דרך המערך בכל פעם. השני, optimizedBubbleSort(int myArray[]) עובר אופטימיזציה על ידי עצירת האלגוריתם אם הלולאה הפנימית לא גרמה להחלפה כלשהי. המונה מראה לך כמה שלבים עשית בזמן המיון. הנה, יש לנו מימוש Java מסוג Bubble:

import java.util.Arrays;

public class BubbleSortExample {

   //  Plane Bubble sort example

   public static int[] bubbleSort(int[] myArray) {

       int temp = 0;  //  temporary element for swapping
       int counter = 0;  //  element to count quantity of steps

       for (int i = 0; i < myArray.length; i++) {
           counter = i + 1;
           for (int j = 1; j < (myArray.length - i); j++) {

               if (myArray[j - 1] > myArray[j]) {
                   //  swap array’s elements using temporary element
                   temp = myArray[j - 1];
                   myArray[j - 1] = myArray[j];
                   myArray[j] = temp;
               }
           }
       }
       System.out.println("Steps quantity, non optimized = " + counter);
       return myArray;
   }
   //  An optimized version of Java Bubble Sorting

   static int[] optimizedBubbleSort(int myArray[]) {
       int temp;
       boolean swapped;
       int counter = 0;  //  element to count quantity of steps
       for (int i = 0; i < myArray.length - 1; i++) {
           counter = i + 1;
           swapped = false;
           for (int j = 0; j < myArray.length - i - 1; j++) {
               //  counter++;
               if (myArray[j] > myArray[j + 1]) {
                   //  swap arr[j] and arr[j+1]
                   temp = myArray[j];
                   myArray[j] = myArray[j + 1];
                   myArray[j + 1] = temp;
                   swapped = true;

               }
           }  //  counter = i;
           //  If there weren't elements to swap in inner loop, then break
           if (swapped == false) {

               break;

           }
       }
       System.out.println("steps quantity, optimized = " + counter);
       return myArray;
   }


   public static void main(String[] args) {
       int arr[] = {8, 7, 1, 2, 5};
       int arr1[] = {8, 7, 1, 2, 5};

       System.out.println("Array arr Before Bubble Sort");
       //  we use java.util.Arrays toString method to print the array
 System.out.println(Arrays.toString(arr));

       System.out.println("Array arr After Bubble Sort");
       System.out.println(Arrays.toString(bubbleSort(arr)));

       System.out.println("Array arr1 Before Bubble Sort");
       System.out.println(Arrays.toString(arr1));

       System.out.println("Array arr1 After Optimized Bubble Sort");
       System.out.println(Arrays.toString(optimizedBubbleSort(arr1)));
   }
}

התוצאה של עבודת אלגוריתם Java מיון בועה:

Array arr Before Bubble Sort
[8, 7, 1, 2, 5]
Array arr After Bubble Sort
Steps quantity, non optimized = 5
[1, 2, 5, 7, 8]
Array arr1 Before Bubble Sort
[8, 7, 1, 2, 5]
Array arr1 After Optimized Bubble Sort
steps quantity, optimized = 3
[1, 2, 5, 7, 8]

עד כמה מיון בועות יעיל?

מיון בועות הוא אחד האלגוריתמים הקלים ביותר ליישום אך הוא אינו יעיל. זה דורש זוג לולאות מקוננות. אפילו בגרסה אופטימלית של אלגוריתם במקרה הגרוע (כל רכיב של מערך הנתונים הוא בסדר הפוך לזה הרצוי) הלולאה החיצונית חוזרת פעם אחת עבור כל אחד מ-n האלמנטים של מערך הנתונים. הלולאה הפנימית חוזרת n פעמים בפעם הראשונה, ( n-1 ) בפעם השנייה, וכן הלאה. לפיכך, כדי למיין את כל הרכיבים n , יש לבצע את הלולאות n*(n-1)/2 פעמים. זה קורא ל- O(n ² ) מורכבות זמן ופירושו שהאלגוריתם עושה בערך 500,000 השוואות עבור 1000 אלמנטים של מערך. עם זאת, אלגוריתם מיון בועות הוא די יעיל בשימוש בזיכרון (מורכבות הזיכרון היא O(n) ) והוא ממש טוב עבור מערכי נתונים קטנים כמעט ממוינים.