אלגוריתמי חיפוש שונים מותאמים למשימות שונות. היום נדבר על חיפוש A*, אחד האלגוריתמים היעילים ביותר לאיתור נתיבים. זה מתאים מאוד למשחקי מחשב ולבניית גרפי חיפוש כגון דרכים בין ערים וכן הלאה. אולי שמתם לב, למשל, במשחקי וידאו אסטרטגיים או טקטיים, כיצד לאחר לחיצה על כפתור, השחקן או הקבוצה שלכם מתחילים מיד ללא דיחוי לעבור את המגרש לנקודה שציינתם. אין עיכוב דווקא בגלל שהמשחקים משתמשים באלגוריתמים יעילים שמחשבים בדיוק איך השחקן צריך להגיע למקום כלשהו. או אויב שמוצא ללא ספק את השחקן ומתחיל ללכת בכיוון הנכון מרחוק. בדרך כלל, האלגוריתם A* משמש לפעולות כאלה.
מהו אלגוריתם A*
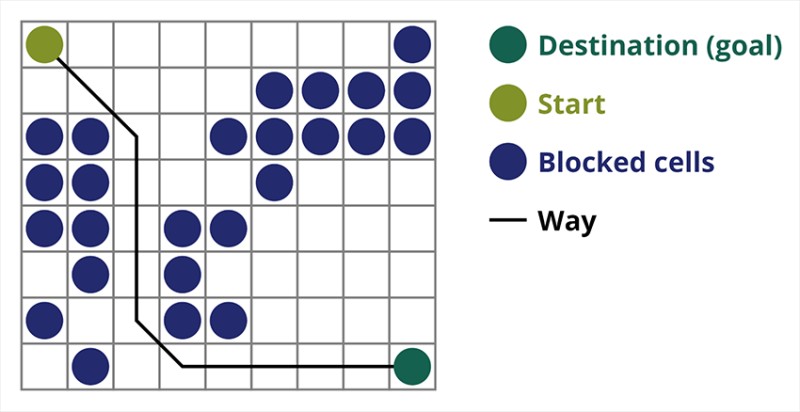
אלגוריתם מציאת נתיבים A* הוא דוגמה לאלגוריתם החיפוש הטוב ביותר. מטרת אלגוריתם A* היא למצוא נתיב מנקודה אחת לאחרת. זו אחת הקלאסיקות לחיפוש אלגוריתמי גרפים. בואו להבין איך זה עובד באמצעות דוגמה. תארו לעצמכם משחק דו מימדי עם תצוגה מלמעלה למטה. בואו נחלק את אזור המשחק שלנו לחמדנות מרובעת, למשל 8*8 תאים כמו לוח שחמט. התאים שלנו יכולים להיות אחד משני סוגים, עבירים או בלתי עבירים (מכשול). בכל פרק זמן שחקן או אויב שמתקרב לשחקן מזיז תא אחד. במשחקים, תאים עבירים יכולים להיות בעלי אופי שונה, למשל כביש שטוח, דשא או חול, מה שקובע את הקושי לנוע לאורכם, אך לשם הפשטות נניח שכל התאים העבירים עוברים באותו אופן. בתמונה למטה, התאים הכחולים הם מכשולים.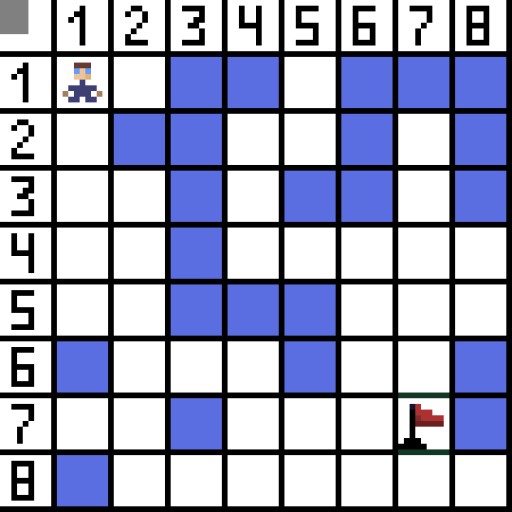
הבה נקצה תא אחד (או צומת) כתא ההתחלה (התו נמצא בו), ואת התא השני כתא היעד או היעד (זה עם הדגל), ונתאר כיצד האלגוריתם A* עובד עבור מקרה זה. הדמות נמצאת בתא (1,1) והמטרה נמצאת בתא (7,7). לכל תא יש שכנים אופקיים, אנכיים ואלכסוניים. זה תלוי במשחק, אם מחשבים צמתים אלכסוניים או לא. לדוגמא במשחקי תצוגה מלמעלה למטה כגון בומברמן או פקמן הדמויות יכולות לנוע רק אופקית או אנכית. במקרה זה לכל צומת, למעט נגיעה בקצוות, יש רק 4 שכנים. אם אנחנו מדברים על משחק שבו דמויות יכולות לנוע באלכסון, לכל צומת יכולים להיות עד 8 שכנים. בשלב הראשון של האלגוריתם, לתא שבו נמצאת הדמות יש שני שכנים. ליתר דיוק, שלושה, אבל אחד מהם מהווה מכשול. 
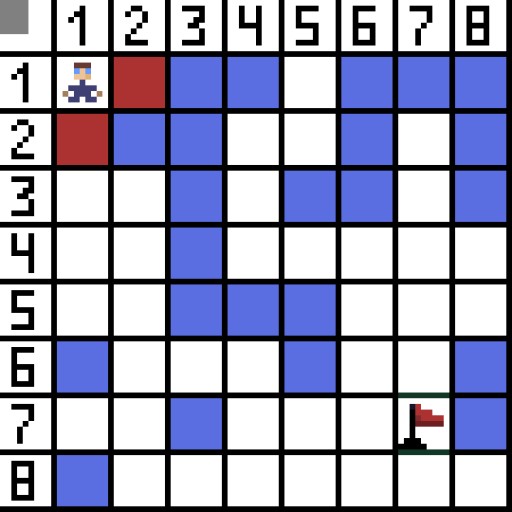ברור שהדרך האלכסונית ארוכה יותר. אם אנו מגדירים את הצלע של התא שלנו להיות שווה בתנאי לאחד, אז אורך האלכסון של התא הזה שווה לשורש הריבועי של שניים. זה מה שאומר משפט פיתגורס. כדי להגיע מתא A לתא B, עליך לבחור תחילה באחד מהתאים הסמוכים, ולאחר מכן את הבא, וכן הלאה. כמו כן, על הדרך להבין האם אפשר להגיע מהתא הראשוני למטרה. אלגוריתם A* בכל שלב בוחר את אחד התאים השכנים בהתאם לערך הפונקציה F. פונקציה זו מודדת עד כמה תא מועמד אמור להיכלל בנתיב הקצר ביותר שלנו. זוהי פונקציית העלות, והיא הסכום של פונקציית התנועה G והפונקציה ההיוריסטית.
-
עלות G - היא מרחק מצומת התחלה.
-
עלות H (היוריסטית) היא מרחק מהצומת הקצה (המטרה). פונקציה זו יכולה להיות שונה, מפתח מחליט מה עדיף. אולי הבחירה ב-H היא החשובה ביותר ב-A*, וזו הנקודה שהופכת כל מימוש מסוים של האלגוריתם ליותר או פחות יעיל. תיאורטית אתה יכול להשתמש בכל פונקציה שתרצה.
במקרה שלנו, אנחנו יודעים את מיקומו של תא המטרה ויכולים, למשל, לחשב מרחק אוקלידי גיאומטרי בין המטרה לתא הנוכחי. ככל שהמרחק קצר יותר, כך אנו קרובים יותר למטרה.
-
F cost = G + H. אז האלגוריתם מחשב את כל העלויות F של הצמתים השכנים ובוחר באחת מהעלויות F הנמוכות ביותר להסתכל עליהן תחילה. כאשר אנו בוחרים אחד אנו מסמנים אותו כסגור ומחשבים ערכים עבור שכני הצומת הזה.
פונקציה היוריסטית כיצד נוכל לחשב H?
זוהי פונקציה היוריסטית. השם עצמו אומר שהוא נקבע על ידי הניסיון, ויכול להיות שונה. כאן ניקח את זה שווה למה שנקרא המרחק האוקלידי בין הנקודות (x1, y1) ו- (x2, y2):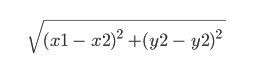
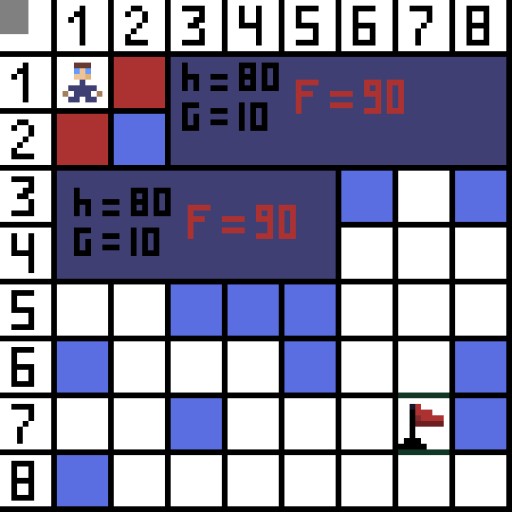בתמונה, בשלב הראשון, יש שתי אפשרויות, והן זהות בעלות, אבל בשלב הבא, הדמות נכנסת למבוי סתום באחת האפשרויות. לכן, אנחנו הולכים בדרך אחרת. באיטרציה הבאה, יש לנו כבר 4 אפשרויות. 
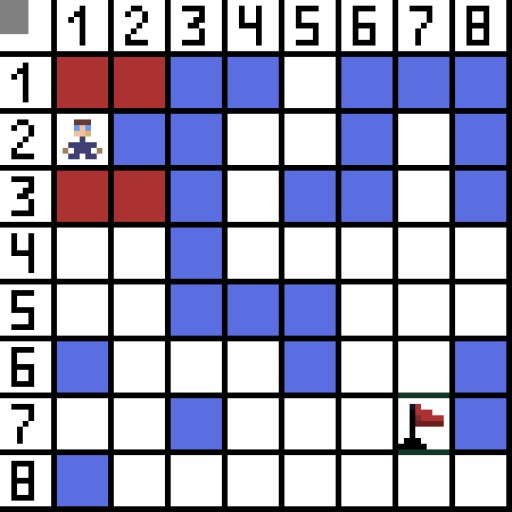שתיים מהן אינן מתאימות, כי הן מובילות לאחור, והאפשרויות האחרות טובות באותה מידה, אבל האלגוריתם החליט שעדיף ללכת באלכסון לתא (3,2). בהמשך, בכל שלב, החישוב של הפונקציה F חוזר על עצמו עד שהתו מגיע לתא המטרה. אם כמובן קיים קטע כזה. 
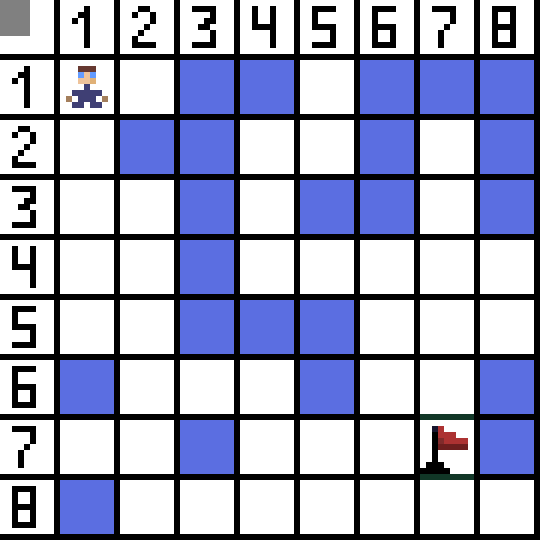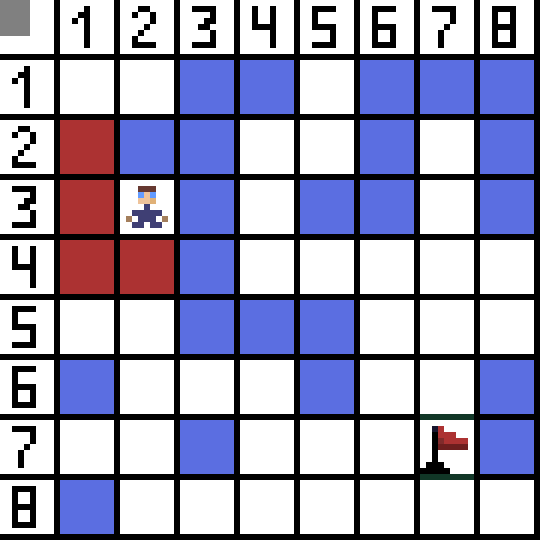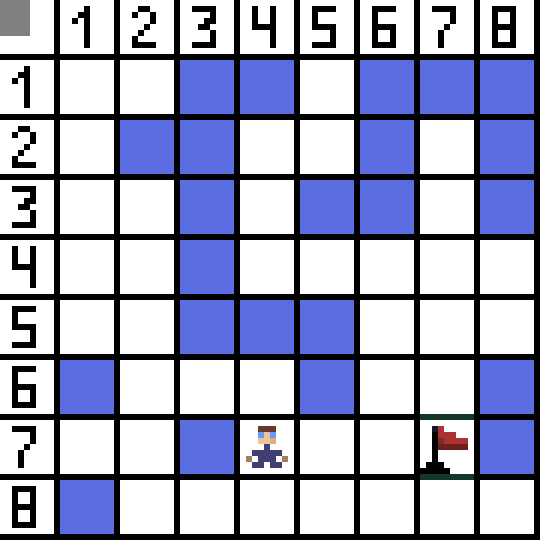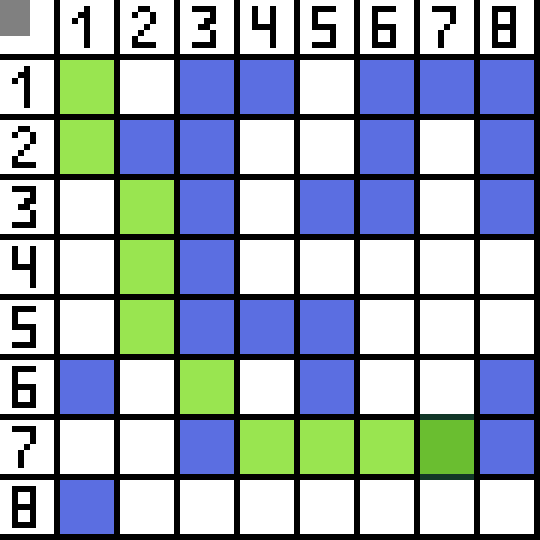דרך ירוקה בתמונת הגיף מציינת את הדרך האופטימלית של הדמות לדגל.
A* אלגוריתם צעד אחר צעד
כדי ליישם את האלגוריתם ב-Java, עליך לבצע את השלבים הבאים 1. ראשית עליך ליצור שתי רשימות, עבור צמתים פתוחים וצמתים סגורים. 2. אתחול שתי הרשימות. ברשימה סגורה, צומת ההתחלה מצביע על הרשימה הפתוחה. 3. בעוד שיש אלמנטים ברשימה הפתוחה: 3א. מצא את הצומת min עם F 3b הקטן ביותר. הסר דקות מהרשימה הפתוחה 3c. קבע שכנים דקות (עד 8, אם לוקחים בחשבון אלכסונים) 3d. בדיקת כל שכן: א) אם השכן הוא תא המטרה, הפסק את החיפוש ב) אם לא, חשב עבורו G, H. G = min.G + מרחק בין שכן ל-min F = G + H c) אם הצומת במיקום זהה לזה של השכן נמצא ברשימה הפתוחה וה-F שלו קטן מזה של השכן, דלג על השכן הזה ד) אם הצומת עם אותו מיקום של השכן נמצא ברשימה הסגורה, וה-f שלו קטן מזה של השכן, דלג על השכן הזה. אחרת, הוסף את הצומת לרשימה הפתוחה סוף לולאה פנימית 3e. הוספת min לרשימה הסגורה סוף הלולאה החיצונית אז, בכל איטרציה אנחנו הולכים לעשות את הדבר הבא:- בחר את התא מהרשימה הפתוחה שלנו עם הציון הכולל המשוער הנמוך ביותר.
- הסר תא זה מהרשימה הפתוחה.
- הוסף את כל התאים שאנו יכולים להגיע ממנו לרשימה הפתוחה.
- כשאנחנו עושים את זה, אנחנו גם מעבדים את הציון החדש מאותו צומת לכל אחד חדש כדי לראות אם זה שיפור ממה שיש לנו עד כה, ואם כן, אנחנו מעדכנים את מה שאנחנו יודעים על התא הזה.
A* פסאודוקוד
הנה פסאודוקוד קצר של חיפוש נתיב A*:Input: a grid with locked and empty cells, with start and goal cell.
Output: least cost path from start to goal cell.
Initialisation
openList = {startCell} //list of traversed cells
closedList = {} //list of already traversed cells
g.startCell = 0 //cost from source cell to a cell
h.startCell = h(startCell, goal) //heuristic
f.startCell = g.startCell + h.StartCell
while openList is not empty
do
//let the currentCell equal the cell with the least f value
currentCell = Cell on top of openList, with least f
if currentCell == end return
remove currentCell from openList
add currentCell to closedList
foreach n in child.currentCell
if n in closedList
continue
cost = g.currentCell + distance(currentCell,n)
if (n in openList and cost < g.n)
remove n from closedList
g.n = cost
h.n = h(n, goal)
f.n = g.n + h.nמפסאודוקוד ליישום A* ב-Java
A* חיפוש נתיבים במימוש Java צריך לכלול כמה שיטות לשרת אלגוריתם:- תא, מבנה להחזיק את הפרמטרים הדרושים
- רשימות פתוחות וסגורות
- שיטה לחישוב פונקציה היוריסטית
- שיטה להתחקות אחר הנתיב מהמקור ליעד
- שיטות לבדוק אם התא הנתון חסום, אם הוא כבר הגיע, אם הוא חוקי וכן הלאה
package Asterist;
import java.util.PriorityQueue;
import java.util.Stack;
public class AAsterisk {
//Java Program to implement A* Search Algorithm
//Here we're creating a shortcut for (int, int) pair
public static class Pair {
int first;
int second;
public Pair(int first, int second){
this.first = first;
this.second = second;
}
@Override
public boolean equals(Object obj) {
return obj instanceof Pair && this.first == ((Pair)obj).first && this.second == ((Pair)obj).second;
}
}
// Creating a shortcut for tuple<int, int, int> type
public static class Details {
double value;
int i;
int j;
public Details(double value, int i, int j) {
this.value = value;
this.i = i;
this.j = j;
}
}
// a Cell (node) structure
public static class Cell {
public Pair parent;
// f = g + h, where h is heuristic
public double f, g, h;
Cell()
{
parent = new Pair(-1, -1);
f = -1;
g = -1;
h = -1;
}
public Cell(Pair parent, double f, double g, double h) {
this.parent = parent;
this.f = f;
this.g = g;
this.h = h;
}
}
// method to check if our cell (row, col) is valid
boolean isValid(int[][] grid, int rows, int cols,
Pair point)
{
if (rows > 0 && cols > 0)
return (point.first >= 0) && (point.first < rows)
&& (point.second >= 0)
&& (point.second < cols);
return false;
}
//is the cell blocked?
boolean isUnBlocked(int[][] grid, int rows, int cols,
Pair point)
{
return isValid(grid, rows, cols, point)
&& grid[point.first][point.second] == 1;
}
//Method to check if destination cell has been already reached
boolean isDestination(Pair position, Pair dest)
{
return position == dest || position.equals(dest);
}
// Method to calculate heuristic function
double calculateHValue(Pair src, Pair dest)
{
return Math.sqrt(Math.pow((src.first - dest.first), 2.0) + Math.pow((src.second - dest.second), 2.0));
}
// Method for tracking the path from source to destination
void tracePath(
Cell[][] cellDetails,
int cols,
int rows,
Pair dest)
{ //A* Search algorithm path
System.out.println("The Path: ");
Stack<Pair> path = new Stack<>();
int row = dest.first;
int col = dest.second;
Pair nextNode = cellDetails[row][col].parent;
do {
path.push(new Pair(row, col));
nextNode = cellDetails[row][col].parent;
row = nextNode.first;
col = nextNode.second;
} while (cellDetails[row][col].parent != nextNode); // until src
while (!path.empty()) {
Pair p = path.peek();
path.pop();
System.out.println("-> (" + p.first + "," + p.second + ") ");
}
}
// A main method, A* Search algorithm to find the shortest path
void aStarSearch(int[][] grid,
int rows,
int cols,
Pair src,
Pair dest)
{
if (!isValid(grid, rows, cols, src)) {
System.out.println("Source is invalid...");
return;
}
if (!isValid(grid, rows, cols, dest)) {
System.out.println("Destination is invalid...");
return;
}
if (!isUnBlocked(grid, rows, cols, src)
|| !isUnBlocked(grid, rows, cols, dest)) {
System.out.println("Source or destination is blocked...");
return;
}
if (isDestination(src, dest)) {
System.out.println("We're already (t)here...");
return;
}
boolean[][] closedList = new boolean[rows][cols];//our closed list
Cell[][] cellDetails = new Cell[rows][cols];
int i, j;
// Initialising of the starting cell
i = src.first;
j = src.second;
cellDetails[i][j] = new Cell();
cellDetails[i][j].f = 0.0;
cellDetails[i][j].g = 0.0;
cellDetails[i][j].h = 0.0;
cellDetails[i][j].parent = new Pair( i, j );
// Creating an open list
PriorityQueue<Details> openList = new PriorityQueue<>((o1, o2) -> (int) Math.round(o1.value - o2.value));
// Put the starting cell on the open list, set f.startCell = 0
openList.add(new Details(0.0, i, j));
while (!openList.isEmpty()) {
Details p = openList.peek();
// Add to the closed list
i = p.i; // second element of tuple
j = p.j; // third element of tuple
// Remove from the open list
openList.poll();
closedList[i][j] = true;
// Generating all the 8 neighbors of the cell
for (int addX = -1; addX <= 1; addX++) {
for (int addY = -1; addY <= 1; addY++) {
Pair neighbour = new Pair(i + addX, j + addY);
if (isValid(grid, rows, cols, neighbour)) {
if(cellDetails[neighbour.first] == null){ cellDetails[neighbour.first] = new Cell[cols]; }
if (cellDetails[neighbour.first][neighbour.second] == null) {
cellDetails[neighbour.first][neighbour.second] = new Cell();
}
if (isDestination(neighbour, dest)) {
cellDetails[neighbour.first][neighbour.second].parent = new Pair ( i, j );
System.out.println("The destination cell is found");
tracePath(cellDetails, rows, cols, dest);
return;
}
else if (!closedList[neighbour.first][neighbour.second]
&& isUnBlocked(grid, rows, cols, neighbour)) {
double gNew, hNew, fNew;
gNew = cellDetails[i][j].g + 1.0;
hNew = calculateHValue(neighbour, dest);
fNew = gNew + hNew;
if (cellDetails[neighbour.first][neighbour.second].f == -1
|| cellDetails[neighbour.first][neighbour.second].f > fNew) {
openList.add(new Details(fNew, neighbour.first, neighbour.second));
// Update the details of this
// cell
cellDetails[neighbour.first][neighbour.second].g = gNew;
//heuristic function cellDetails[neighbour.first][neighbour.second].h = hNew;
cellDetails[neighbour.first][neighbour.second].f = fNew;
cellDetails[neighbour.first][neighbour.second].parent = new Pair( i, j );
}
}
}
}
}
}
System.out.println("Failed to find the Destination Cell");
}
// test
public static void main(String[] args) {
//0: The cell is blocked
// 1: The cell is not blocked
int[][] grid = {
{ 1, 1, 0, 0, 1, 0, 0, 0 },
{ 1, 0, 0, 1, 1, 0, 1, 0 },
{ 1, 1, 0, 1, 0, 0, 1, 0 },
{ 1, 1, 0, 1, 1, 1, 1, 1 },
{ 1, 1, 0, 0, 0, 1, 1, 1 },
{ 0, 1, 1, 1, 0, 1, 1, 0 },
{ 1, 1, 0, 1, 1, 1, 1, 0 },
{ 0, 1, 1, 1, 1, 1, 1, 1 }
};
// Start is the left-most upper-most corner
Pair src = new Pair(0,0);
//(8, 0);
// Destination is the right-most bottom-most corner
Pair dest = new Pair(6, 6);
AAsterisk app = new AAsterisk();
app.aStarSearch(grid, grid.length , grid[0].length, src, dest);
}
}
הנתיב: -> (0,0) -> (1,0) -> (2,1) -> (3,1) -> (4,1) -> (5,2) -> (5, 3) -> (6,4) -> (6,5) -> (6,6)
ניתן לראות כי זהו אחד מכמה שבילים הקצרים ביותר שניתן לבנות בין שתי הנקודות הללו. שימו לב שהשלב השישי בדוגמה שלנו בתמונה ובפלט התוכנית שונה, אם כי הנתיבים התבררו כיעילים באותה מידה. התוכנית בוחרת באחת מהאפשרויות היעילות ביותר.
GO TO FULL VERSION