جاوا ۾ ميڪس هيپ

بائنري وڻ

جاوا ۾، ڊيٽا جي جوڙجڪ جا ڪيترائي مختلف قسم آهن. هيپ هڪ وڻ جي جوڙجڪ تي ٻڌل آهي جنهن کي بائنري وڻ سڏيو ويندو آهي . هڪ بائنري وڻ نوڊس تي مشتمل هوندو آهي، جن مان هر هڪ ۾ وڌ ۾ وڌ 2 چائلڊ نوڊس هوندا آهن: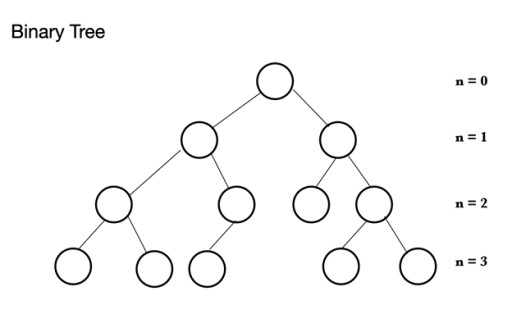 هڪ بائنري وڻ هڪ پيرن نوڊ تي مشتمل هوندو آهي جنهن ۾ 0 کان 2 نوڊس هوندا آهن. اهو ٿي سگهي ٿو هڪ کاٻي ٻار جو نوڊ ۽ / يا ساڄي ٻار جو نوڊ، يا ڪو به نوڊس ڪونهي. هڪ مڪمل بائنري وڻ ۾، سڀ نوڊس ڀرجي ويا آهن سواءِ آخري ليول جي جيڪو مڪمل ٿي سگهي ٿو، پر مڪمل ٿيڻ جي ضرورت ناهي. آخري سطح، nth سطح، ٿي سگھي ٿو 1 کان 2n نوڊس، جتي پھريون آھي n = 0 ۽ روٽ آھي.

وڌ ۾ وڌ هيپ

Max heap (يا maxheap) هڪ مڪمل بائنري وڻ آهي . ان جي باري ۾ اهم شيء اها آهي ته والدين نوڊ کي لازمي طور تي هڪ قدر هجڻ گهرجي ان کان وڌيڪ يا برابر جو کاٻي ۽ ساڄي ٻار جي نوڊس. جيڪڏهن اهو عمل نه ڪيو ويو آهي، توهان وٽ وڌ ۾ وڌ هيپ نه آهي. منٽ هيپ، ٻئي طرف، روٽ سان برعڪس آهي جيئن ته ننڍي ۾ ننڍي قدر، لڳاتار نوڊس سان قدر ۾ وڌندي؛ هر ٻار جي نوڊ جو قدر ان جي والدين کان وڌيڪ يا برابر هوندو آهي. اهو پڻ هڪ مڪمل بائنري وڻ آهي. وڌ ۾ وڌ هيپ جو هڪ مثال آهي: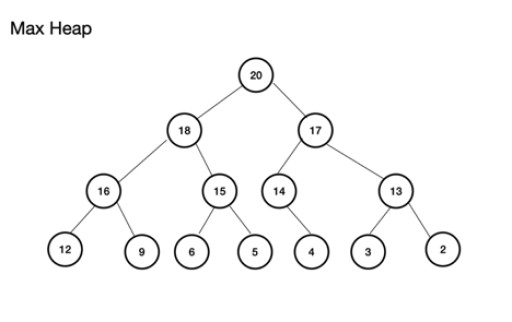 وڌ ۾ وڌ هيپ هڪ صف مان ٺاهي سگهجي ٿو. هن صف کي هڪ وڻ جي لحاظ کان سوچيو ويندو. هڪ ڍير لاءِ، جيڪڏهن روٽ، (وڻ جو مٿئين پيرين نوڊ) پوزيشن (انڊيڪس) n تي ذخيرو ٿيل آهي، ان جي وضاحت ڪئي وئي آهي array، theArray ، جيئن theArray[n] . کاٻي ۽ ساڄي ٻار جا نوڊس آهن، تنهن ڪري، ترتيب سان TheArray[2n+1] ۽ TheArray[2n+2] تي . وڌ ۾ وڌ هيپ لاءِ، روٽ آهي Array[0] تي . ليول n لاءِ، روٽ n = 0: theArr[n] والدين نوڊ آھي TheArr[(2*n)+1] کاٻي ٻار جو نوڊ آھي Arr[(2*n)+2] ساڄي ٻار جو نوڊ آھي

ترجيحي قطار ڪلاس

جاوا ۾ هيپس کي لاڳو ڪري سگھجي ٿو PriorityQueue Class استعمال ڪندي. PriorityQueues استعمال ڪيا ويندا آھن ھڪڙي مجموعي ۾ سڀ کان وڌيڪ يا گھٽ ۾ گھٽ اھم شيءِ ڳولڻ لاءِ. PriorityQueue ڪلاس java.util.package ۾ ڳولهي سگھجي ٿو . PriorityQueues انهن شين مان ٺهڻ گهرجن جيڪي تقابلي هجن ته جيئن اهي قطار ۾ هڪ خاص ترتيب ۾ رکيا وڃن. PriorityQueue ۾ هڪ comparator ٿي سگهي ٿو ته جيئن شين جي وچ ۾ هڪ مقابلو ڪيو وڃي ۽ قطار هن مقابلي جي مطابق ٺاهي وئي. هڪ مثال آهي:

import java.util.Comparator;
import java.util.PriorityQueue;

public class Main
{
    public static void main(String[] args) {
        // Create PriorityQueue with comparator for ascending order of array length
        PriorityQueue intQueue = new PriorityQueue((a,b) -> a - b);
        Integer [] array1 = {1, 2, 4, 6, 8, 9};
        Integer [] array2 = {3, 6, 9};
        Integer [] array3 = {2, 4, 8, 16, 32, 64, 128};
        Integer [] array4 = {5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55};
        Integer [] array5 = {4};

        //Add the array lengths to intQueue
        intQueue.add(array1.length);
        intQueue.add(array2.length);
        intQueue.add(array3.length);
        intQueue.add(array4.length);
        intQueue.add(array5.length);
        //Write out contents of intQueue as stored
        while (intQueue.size() != 0) {
            System.out.println(intQueue.remove());
        }
    }
}

پيداوار ڏيڻ: ھن مثال ۾، intQueue جي ڊفالٽ سائيز 11 آھي، تنھنڪري بيان نه ڪيو ويو آھي (عام طور تي پھريون دليل comparator کان اڳ) ۽ comparator ڏنو ويو آھي جيئن: هي intQueue ۾ شيون جي وچ ۾ هڪ مقابلو ڪندو ۽ ان کي ترتيب ڏئي ترتيب جي ڊيگهه جي ترتيب ۾.

وڌ ۾ وڌ هيپ ٺاهڻ لاءِ ترجيحي قطار جو نفاذ

PriorityQueue Class defaults min heap to be comparator. منٽ هيپ وڌ ۾ وڌ هيپ جي برعڪس آهي ۽ تنهنڪري روٽ سڀ کان ننڍو قدر آهي ۽ لڳاتار چائلڊ نوڊس وڏا يا برابر هوندا آهن روٽ ۽ بعد ۾ والدين جي نوڊس. انهي سبب لاء، وڌ ۾ وڌ هيپ لاء، استعمال ڪرڻ ضروري آهي reverseOrder() جاوا جي ڪليڪشن فريم ورڪ مان comparator طور. اهو يقيني بڻائيندو ته اسان هڪ وڌ ۾ وڌ ڍير حاصل ڪندا آهيون ۽ نه هڪ منٽ هيپ. ھن ڪلاس ۾ مفيد طريقا آھن جھڙوڪ add() , contains() , remove() , poll() , and peek() . عناصر قطار ۾ شامل ڪيا ويا آهن ۽ ڪنهن به ترتيب ۾ ٿي سگهي ٿو. نئين PriorityQueue قطار انهن عناصر کي ريورس آرڊر ۾ وڌ ۾ وڌ هيپ طور ذخيرو ڪندو. جڏهن قطار لکجي ويندي آهي، آرڊر ٿيندو: روٽ کاٻي ٻار روٽ سان والدين جي حيثيت سان (کاٻي ٻار_1) ساڄي ٻار روٽ سان والدين جي حيثيت سان (ساڄي ٻار_1) کاٻي ٻار کاٻي ٻار سان گڏ والدين طور (کاٻي ٻار_2) ) کاٻي ٻار سان گڏ کاٻي ٻار_1 والدين طور (ساڄي ٻار_2) کاٻي ٻار ساڄي ٻار سان_1 والدين طور (کاٻي ٻار_3) ساڄي ٻار ساڄي ٻار سان_1 والدين طور (ساڄي ٻار_3) کاٻي ٻار کاٻي ٻار سان_2 as parent (Left-child_4) Right-child with Left-child_2 as parent (Right-child_4) وغيره هيٺ ڏنل ڪوڊ هڪ مثال آهي ته ڪيئن هڪ max heap (maxheap) java ۾ ٺاهي وئي آهي. ڪرڻ لاءِ پهرين شيءِ آهي هڪ صف ڀرڻ لاءِ قدرن سان جنهن لاءِ وڌ ۾ وڌ هيپ ٺاهي ويندي. هي Array سڏيو ويندو آهي . اڳيون، هڪ PriorityQueue ، the Queue ، ٺاهي وئي آهي ۽ پوءِ Array مان عناصر هن ۾ شامل ڪيا ويا آهن. هي طريقو استعمال ڪري ٿو add() ، مثال طور theQueue.add(10) قطار جي آخر ۾ 10 شامل ڪرڻ لاءِ. PriorityQueue ڪلاس جي ڪجھ ڪارڪردگيءَ کي واضع ڪرڻ لاءِ ، طريقو peek() استعمال ڪيو ويندو آھي پوءِ ھيڊ جي سر کي ڳولڻ لاءِ، ۽ اھو وڌ ۾ وڌ قدر آھي، ھن صورت ۾، 99. ايندڙ ڪم ھيپ جي سائيز کي جانچڻ آھي. استعمال ڪندي size() جيڪو مليو آهي 9 ۽ اهو ڇپيل آهي ڪنسول ڏانهن. طريقو لکڻ ميڪس هيپ قطار ۾ عناصرن کي روٽ جي ترتيب سان لکي ٿو، کاٻي ٻار کي روٽ سان والدين طور، ساڄي ٻار روٽ سان والدين طور، کاٻي ٻار پهرين کاٻي ٻار سان والدين طور، ساڄي ٻار پهرين کاٻي ٻار سان گڏ والدين، ساڄي ٻار سان گڏ پهرين ساڄي ٻار سان والدين طور، کاٻي ٻار سان گڏ پهرين ساڄي ٻار سان والدين وانگر، بعد ۾ قدرن سان گڏ کاٻي ۽ ساڄي ٻارن کي والدين طور استعمال ڪندي ساڳئي ترتيب ۾ مٿي ڏنل ترتيب ۾. PriorityQueue طريقو شامل آهي (J) استعمال ڪيو ويندو آهي اهو معلوم ڪرڻ لاءِ ته ڇا هڪ مخصوص عنصر، J، قطار ۾ آهي. ھن حالت ۾ اسين ڳوليندا آھيون J = 10. اسان جي مثال ۾، اھو صحيح آھي ته ھي قطار ۾ آھي، تنھنڪري ھن کي ڪنسول ڏانھن سچو لکيو ويو آھي. ٻيو PriorityQueue طريقو، remove(J) پوءِ استعمال ڪيو ويندو آهي J = 10 کي قطار مان هٽائڻ لاءِ . PriorityQueue جي وڌيڪ ڪارڪردگي کي واضع ڪرڻ لاء ، طريقو پول() استعمال ڪيو ويندو آهي هيڊ عنصر (وڌ کان وڌ قدر) کي هٽائڻ لاءِ جڏهن ته لوپ استعمال ڪندي، هر دفعي نئين قطار ۾ هيڊ عنصر کي هٽائڻ ۽ هر دفعي قطار جي سائيز کي گهٽائيندي. اهو طريقو لکڻ جي قطار ۾ ٿئي ٿو جنهن کي مين کان سڏيو ويندو آهي. هر دفعي هٽايو ويو عنصر کنسول تي ڇپيل آهي. اصل قطار ۾ آخرڪار ڪو به عنصر نه بچندو. پرنٽ ٿيل عناصر قيمت جي ھيٺئين ترتيب ۾ وڌ ۾ وڌ ڍير آھن، جتي قطار جو مٿو ھر دفعي پرنٽ ڪيو ويندو آھي.

mport java.util.Collections;
import java.util.PriorityQueue;

public class MaxHeap {

       public static void writeQueue(PriorityQueue<Integer> priorityQueue)
       {
           // Write out elements in queue, priorityQueue, and remove them using poll()
           while(priorityQueue.size() != 0)
           {
               System.out.println(priorityQueue.poll());
           }
       }

       public static void writeMaxHeap(PriorityQueue<Integer> priorityQueue)
       {
           // Write out elements in queue as a max heap - root, left child, right child, etc
           for (Integer element : priorityQueue) {
               System.out.println(element);
           }
       }

       public static void main(String args[])
       {
           // Array of numbers to create a max heap array from
           int[] theArray = {5, 3, 13, 10, 99, 19, 6, 51, 9};

           // theQueue is created
           PriorityQueue<Integer> theQueue =
                   new PriorityQueue<Integer>(Collections.reverseOrder());

           // Elements are added to theQueue
           for (int i = 0 ; i <theArray.length; ++i)
           {
               theQueue.add(theArray[i]);
           }

           // The head or root element (priority element) is printed out
           System.out.println("The root value is : " +  theQueue.peek());

           // Find size of theQueue. Use method size()
           Integer s = theQueue.size();
           System.out.println("Size of theQueue? " + s);

           // All elements of theQueue are printed in terms of parent,
           // left child, right child
           System.out.println("theQueue written using for loop:");
           writeMaxHeap(theQueue);

           // Does theQueue contain 10? Use method contains()
           boolean b = theQueue.contains(10);
           System.out.println("Does theQueue contain 10? " + b);

           // Erasing value 10 from array using remove()
           theQueue.remove(10);

           // All elements of theQueue are printed out and removed.
           // Each one is the maximum value left in the queue.
           // At the end theQueue will be empty
           System.out.println("theQueue written out using poll():");
           writeQueue(theQueue);

           // Find size of theQueue. Use method size()
           s = theQueue.size();
           System.out.println("Size of theQueue? " + s);
       }
   }

پيداوار:

Max Heapify

Max Heapify الگورتھم استعمال ڪيو ويندو آھي يقيني بڻائڻ لاءِ ته ھڪڙو بائنري وڻ ھڪڙو وڌ ۾ وڌ ھيپ آھي. جيڪڏهن اسان هڪ نوڊ تي آهيون، n، ۽ ان جي چائلڊ نوڊس، کاٻي ۽ ساڄي به پاڻ ۾ وڌ ۾ وڌ هيپس آهن، پوءِ وڏو، اسان وٽ وڌ ۾ وڌ ڍير آهي. جيڪڏهن سڄي وڻ ۾ ائين نه آهي ته پوءِ اسان وٽ وڌ ۾ وڌ ڍير نه آهي. Max Heapify الگورتھم استعمال ڪيو ويندو آھي وڻ کي ترتيب ڏيڻ لاءِ ته جيئن اھو maxheap اصولن تي عمل ڪري. Max Heapify صرف هڪ نوڊ تي ڪم ڪري ٿو. جيڪڏهن گهرج اها آهي ته صف هڪ وڌ ۾ وڌ هيپ صف آهي، پوء سڀني ذيلي وڻن کي روٽ کان اڳ maxheap ۾ تبديل ڪيو وڃي، هڪ وقت ۾. الورورٿم هر نوڊ تي استعمال ٿيڻ گهرجي. اهو N/2 نوڊس تي ڪيو ويندو (پتي وڌ ۾ وڌ هيپ گهرجن تي عمل ڪندي). هيپ جي وقت جي پيچيدگي O (NlogN) آهي، ۽ اوچائي X تي هڪ نوڊ لاء، وقت جي پيچيدگي O (X) آهي. هيٺ ڏنل ڪوڊ ڏيکاري ٿو ته ڪيئن وڌ ۾ وڌ هڪ وڻ (هڪ صف) کي وڌايو.

public class MaxHeapify

{
   public static Integer[] maxHeapify(Integer[ ] array, Integer i)
   {
       // Create left-child and right-child for the node in question
       Integer leftChild = 2 * i + 1;
       Integer rightChild = 2 * i + 2;

       // Assign maxVal to parent node, i
       Integer maxVal = i;

       // Set maxVal to greater of the two: node or left-child
       if( leftChild < array.length && array[leftChild] > array[maxVal] )
           maxVal = leftChild;

       // Set maxVal to greater of the two: maxVal or right-child
       if( rightChild < array.length && array[rightChild] > array[maxVal] )
           maxVal = rightChild;

       // Check if maxVal is not equal to parent node, then set parent node to
       // maxVal, swap values and then do a maxheapify on maxVal
       // which is now the previous parent node
       if( maxVal != i )
       {
           Integer value = array[i];
           array[i] = array[maxVal];
           array[maxVal] = value;
           array = maxHeapify(array, maxVal);
       }

       return array;
   }


   public static Integer[] maxHeapCreate(Integer array[])
   {
       // Call maxHeapify to arrange array in a max heap
       Integer [] theNewArr = array;
       for( Integer i = array.length/2; i >= 0; i-- )
           theNewArr = maxHeapify(array, i);

       return theNewArr;
   }

   public static void main(String[] args)
   {
       // Create array to be maxheapified, theArray,
       // and array, newArray, to write results into, by calling maxheapCreate
       // newArray will now be a maxheap
       Integer[] theArray = {5, 3, 13, 10, 99, 19, 6, 51, 9};
       Integer[ ] newArray = maxHeapCreate(theArray);

       // Print out contents of newArray
       System.out.println("newArray:");
       for(int i = 0; i < newArray.length; ++i)
       {
           System.out.println(newArray[i]);
       }

       // Print out labelled contents of newArray
       System.out.println(" root : " + newArray[0]);
       for (int i = 0; i <= newArray.length/2 - 1; i++) {
           System.out.print(" parent node : " + newArray[i] + " left child : " +
                            newArray[(2*i)+1] + " right child :" + newArray[(2*i)+2]);
           System.out.println();
       }
  }
}

پيداوار ڏيڻ: ھن ڪوڊ ۾، Array ٺاھيو ويو آھي ۽ انگن سان ڀريل آھي. هڪ ٻيو صف، newArray ، ٺاهيو ويو آهي ۽ هن ڀيري اهو طريقو جو نتيجو هوندو، maxheapCreate , max heap array. طريقو maxHeapCreate کي main مان سڏيو ويندو آهي ، ۽ هتي هڪ نئين صف، TheNewArr ، ٺاهي وئي آهي ۽ maxHeapify نتيجن سان ڀريل آهي . اهو انپٽ صف جي اڌ کان مٿي لوپ ڪندي ڪيو ويندو آهي. لوپ جي هر پاس لاء، طريقو maxHeapify ، سڏيو ويندو آهي عنصر کان شروع ٿيندڙ صف جي وچ ۾ ۽ پهرين سان ختم ٿيڻ. maxHeapify جي هر ڪال لاءِ ، والدين نوڊ جو کاٻي ٻار ۽ ساڄي ٻار، i، مليا ويندا آهن ۽ چيڪ ڪيا ويندا آهن ته معلوم ڪرڻ لاءِ ته ٽن مان سڀ کان وڏو ڪهڙو آهي، جنهن جي وضاحت ڪندي maxVal . جيڪڏهن maxVal والدين نوڊ جي برابر نه آهي ته پوءِ هڪ ادل بدليو وڃي ٿو ته جيئن پيرنٽ نوڊ ۽ maxVal کي تبديل ڪيو وڃي ۽ پوءِ maxHeapify کي ٻيهر سڏيو وڃي ٿو هن ڀيري maxVal تي ۽ ساڳيا قدم اڳ ۾ ڪيا ويا. آخرڪار وڌ ۾ وڌ ڍير ٺاهي ويندي ۽ اڳتي وڌڻ لاءِ وڌيڪ ورجاءُ نه ٿيندو. اپڊيٽ ڪيل صف، صف ، ھاڻي اصلي ڏانھن موٽيو ويو آھي نئين آرري طور ۽ پوءِ ھر لڳاتار عنصر ڪنسول ڏانھن پرنٽ ڪيو ويو. newArray هاڻي وڌ ۾ وڌ هيپ آهي. نوٽ، جيئن اڳئين مثال ۾ PriorityQueue استعمال ڪندي انگ لکيا ويا آهن: روٽ، ساڄي ٻار جو روٽ والدين طور، کاٻي ٻار جو روٽ والدين طور، ساڄي ٻار جو پهريون ساڄي ٻار والدين طور، کاٻي ٻار جو پهريون کاٻي ٻار کي والدين طور، ساڄي ٻار جو پهريون کاٻي ٻار جو والدين طور، کاٻي ٻار جو پهريون ساڄي ٻار جو والدين طور، وغيره. اهي انهن کان ٿورڙي مختلف ترتيب ۾ آهن جڏهن PriorityQueue استعمال ڪندا آهن ڇاڪاڻ ته مقابلو لڳاتار عناصر جي وچ ۾ ڪيو ويندو آهي جڏهن ته maxheapify مثال ۾، نوڊ کي صف ۾ ايندڙ ٻن لڳاتار عناصر سان مقابلو ڪيو ويو آهي ۽ سڀ کان وڏي قيمت لاء تبديل ڪيو ويو آهي. مختصر ۾، ٻه مختلف الگورتھم استعمال ڪيا ويا آھن. ٻئي هڪ وڌ ۾ وڌ ڍير ٺاهي.

نتيجو

تنهنڪري هتي اسان ڏٺو آهي وڌ ۾ وڌ هيپ ۽ اهو ڪيئن ٺاهي سگهجي ٿو يا ته هڪ PriorityQueue يا Max Heapify الگورتھم سان. استعمال ڪندي PriorityQueue سان reverseOrder() اهو ڪرڻ جو هڪ صاف طريقو آهي ۽ تجويز ڪيل طريقو. تنهن هوندي، توهان انهن مثالن جو مطالعو ڪري سگهو ٿا ۽ پنهنجا پنهنجا طريقا لکي سگهو ٿا ڇو ته اهو هڪ سٺو ڪوڊنگ مشق هوندو جيڪو توهان جي جاوا جونيئر لاءِ توهان جي انٽرويو ۾ ڪامياب ٿيڻ ۾ مدد ڪندي.