نوڪريءَ جي انٽرويوز کان سوال ۽ جواب: جاوا ۾ الگورتھم، حصو 2

هي الگورتھم جي مختصر جائزو جو ٻيو حصو آهي. هتي پهرين مضمون جي لنڪ آهي . ان کان اڳ اسان صفن کي ترتيب ڏيڻ لاءِ مختلف الگورتھم کي ڏٺو ۽ ان سان گڏ نام نهاد لالچي الگورتھم. اڄ اسان گرافس ۽ انهن سان لاڳاپيل الگورتھم بابت ڳالهائينداسين. هڪ گراف پروگرامنگ ۾ سڀ کان وڌيڪ لچڪدار ۽ ورڇيل جوڙجڪ مان هڪ آهي. گراف G عام طور تي سيٽ جي هڪ جوڙي جي وضاحت ڪئي وئي آهي، يعني G = (V، R)، جتي:

• V عمودي جو هڪ سيٽ آهي؛
• R قطارن جو هڪ مجموعو آهي جيڪو ڪنيڪشن جي جوڙن کي ڳنڍيندو آهي.

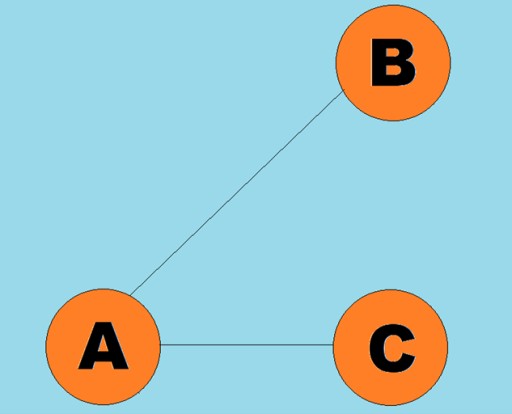اڻ سڌي طرح ڳنڍيندڙ لائينن کي ڪنڊن (Edges) چئبو آهي: سڌي طرح لڪيرن کي آرڪ چئبو آهي: 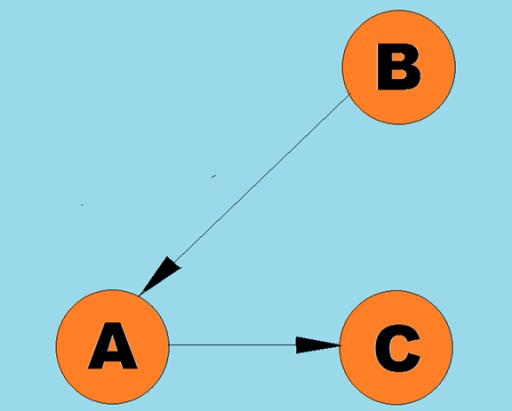عام طور تي، هڪ گراف کي ڊاگرام ذريعي ظاھر ڪيو ويندو آھي، جنھن ۾ ڪن ڪنارن (آرڪز) جي ذريعي ڪجھ عمودي ڳنڍيل آھن. اهي گراف جن جا ڪنارا ٽرورسل جي طرف اشارو ڪن ٿا انهن کي هدايت ٿيل گراف سڏيو ويندو آهي. جيڪڏهن هڪ گراف ڪنارن سان ڳنڍيل آهي جيڪو لنگر جي طرف اشارو نٿو ڪري، پوء اسان چئون ٿا ته اهو هڪ اڻ سڌي گراف آهي. ان جو مطلب اهو آهي ته حرڪت ٻنهي طرفن ۾ ممڪن آهي: ٻئي عمدي A کان vertex B تائين، ۽ vertex B کان vertex A تائين. A جڙيل گراف هڪ گراف آهي جنهن ۾ گهٽ ۾ گهٽ هڪ رستو هر ويرٽيڪس کان ٻئي عميق ڏانهن وڃي ٿو (جيئن ته مثال مٿي). جيڪڏهن اهو معاملو نه آهي، ته پوء گراف کي ختم ڪيو ويو آهي: 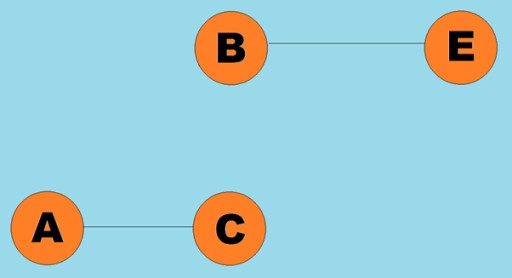وزن پڻ ڪنارن تي مقرر ڪري سگهجي ٿو (آرڪس). وزن اھي انگ آھن جيڪي نمائندگي ڪن ٿا، مثال طور، ٻن چوڪن جي وچ ۾ جسماني فاصلو (يا ٻن چوڪن جي وچ ۾ لاڳاپو سفر جو وقت). انهن گرافس کي وزني گراف سڏيو ويندو آهي: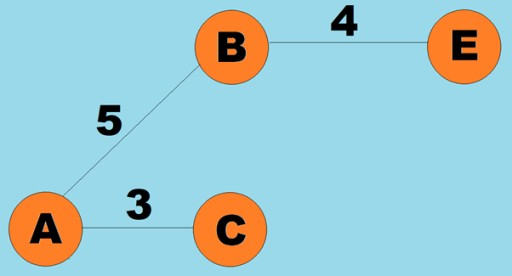

3. پاٿ فائنڊنگ الگورتھم (ڊپٿ فرسٽ، بيڊٿ فرسٽ)

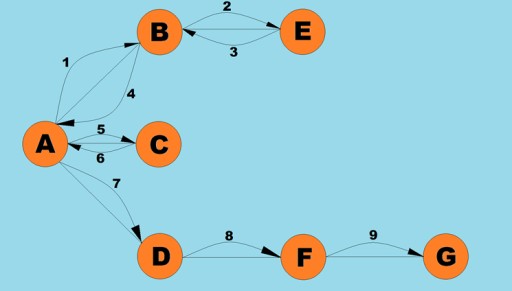
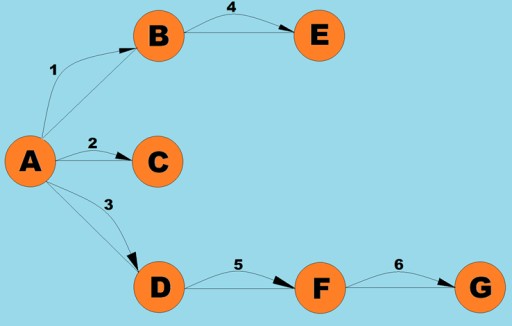
گراف سان گڏ ڪيل بنيادي عملن مان ھڪڙو مقرر ڪيل سڀني چوڪن کي مقرر ڪرڻ آھي جيڪو ھڪڙي ڏنل عمدي کان پھچي سگھي ٿو. تصور ڪريو ته توهان اهو طئي ڪرڻ جي ڪوشش ڪري رهيا آهيو ته توهان هڪ شهر کان ٻئي شهر تائين ڪيئن سواري ڪري سگهو ٿا، ممڪن منتقلي سميت. ڪجهه شهرن تائين سڌو پهچي سگهجي ٿو، جڏهن ته ڪجهه صرف ٻين شهرن مان گذرڻ سان پهچي سگهجي ٿو. اتي ٻيون به ڪيتريون ئي حالتون آھن جتي توھان کي ضرورت پئجي سگھي ٿي ته توھان انھن سڀني چوڪن کي ڳولھيو جيڪي توھان ھڪڙي ڏنل عمدي مان پھچي سگھو ٿا. گراف کي ڇڪڻ جا ٻه مکيه طريقا آهن: کوٽائي-پهرين ۽ ويڪر-پهريون. اسان انهن ٻنهي جي ڳولا ڪنداسين. ٻئي طريقا سڀني جڙيل چوڪن کي پار ڪن ٿا. وڌيڪ ڳولھڻ لاءِ ڊيپٿ فرسٽ ۽ بيڊٿ فرسٽ الگورٿمز، اسان ھيٺ ڏنل گراف استعمال ڪنداسين:

کوٽائي - پهرين ڳولا

هي سڀ کان عام گراف ٽرورسل طريقن مان هڪ آهي. گہرائي-پهريون حڪمت عملي آهي جيترو ٿي سگهي گراف ۾ اوترو اونهو وڃڻ. ان کان پوءِ ختم ٿيڻ کان پوءِ، اسان ويجھي ويجھي چوٽي ڏانھن موٽي وڃون ٿا، جيڪو اڳ ۾ ويجھي ويجھي چوٽيءَ کي نه ڏٺو ويو ھو. هي الورورٿم اسٽيڪ تي معلومات محفوظ ڪري ٿو ته ڪٿي واپس وڃڻو آهي جڏهن هڪ ختم ٿيڻ تي پهچي وڃي. کوٽائي-پهريون ڳولا جا ضابطا:

1. اڳئين اڻ ڏٺل ويجھي ويڪر جو دورو ڪريو، ان کي نشان لڳايو جيئن دورو ڪيو ويو، ۽ ان کي اسٽيڪ تي دٻايو.
2. هن عمدي ڏانهن وڃو.
3. ورجايو قدم 1.
4. جيڪڏهن قدم 1 ناممڪن آهي، ته پوئين ويڪر ڏانهن واپس وڃو ۽ قدم 1 کي انجام ڏيڻ جي ڪوشش ڪريو. جيڪڏهن اهو ممڪن نه آهي، ته ان کان اڳ واري ويڪر ڏانهن واپس وڃو، ۽ ائين ئي، جيستائين اسان کي هڪ عمدي نه ملي، جتان اسان ٽرورسل جاري رکي سگهون.
5. جاري رکو جيستائين سڀئي عمودي اسٽيڪ تي آهن.

اچو ته هڪ نظر رکون ته هن الگورتھم لاءِ جاوا ڪوڊ ڇا نظر اچي ٿو:

public class Graph {
  private final int MAX_VERTS = 10;
  private Vertex vertexArray[]; // Array of vertices
  private int adjMat[][]; // Adjacency matrix
  private int nVerts; // Current number of vertices
  private Stack stack;

  public Graph() { // Initialize internal fields
     vertexArray = new Vertex[MAX_VERTS];
     adjMat = new int[MAX_VERTS][MAX_VERTS];
     nVerts = 0;
     for (int j = 0; j < MAX_VERTS; j++) {
        for (int k = 0; k < MAX_VERTS; k++) {
           adjMat[j][k] = 0;
        }
     }
     stack = new Stack<>();
  }

  public void addVertex(char lab) {
     vertexArray[nVerts++] = new Vertex(lab);
  }

  public void addEdge(int start, int end) {
     adjMat[start][end] = 1;
     adjMat[end][start] = 1;
  }

  public void displayVertex(int v) {
     System.out.println(vertexArray[v].getLabel());
  }

  public void dfs() { // Depth-first search
     vertexArray[0].setVisited(true); // Take the first vertex
     displayVertex(0);
     stack.push(0);

     while (!stack.empty()) {
        int v = getAdjUnvisitedVertex(stack.peek()); // Return the index of the adjacent vertex: if any, 1; if not, -1
        if (v == -1) { // If there is no unvisited adjacent vertex
           stack.pop(); // The element is removed from the stack
        }
        else {
           vertexArray[v].setVisited(true);
           displayVertex(v);
           stack.push(v); // The element goes on top of the stack
        }
     }

     for (int j = 0; j < nVerts; j++) {  // Reset the flags
        vertexArray[j].visited = false;
     }

  }

  private int getAdjUnvisitedVertex(int v) {
     for (int j = 0; j < nVerts; j++) {
        if (adjMat[v][j] == 1 && vertexArray[j].visited == false) {
           return j; // Returns the first vertex found
        }
     }
     return -1;
  }
}

هڪ ويڪر هن طرح نظر اچي ٿو:

public class Vertex {
  private char label;  // for example, 'A'
  public boolean visited;

  public Vertex(final char label) {
     this.label = label;
     visited = false;
  }

  public char getLabel() {
     return this.label;
  }

  public boolean isVisited() {
     return this.visited;
  }

  public void setVisited(final boolean visited) {
     this.visited = visited;
  }
}

اچو ته هن الگورتھم کي مخصوص ڪنارن سان هلون ۽ ڏسو ته اهو صحيح ڪم ڪري ٿو:

public class Solution {
  public static void main(String[] args) {
     Graph graph = new Graph();
     graph.addVertex('A'); //0
     graph.addVertex('B'); //1
     graph.addVertex('C'); //2
     graph.addVertex('D'); //3
     graph.addVertex('E'); //4
     graph.addVertex('F'); //5
     graph.addVertex('G'); //6

     graph.addEdge(0,1);
     graph.addEdge(0,2);
     graph.addEdge(0,3);
     graph.addEdge(1,4);
     graph.addEdge(3,5);
     graph.addEdge(5,6);

     System.out.println("Visits: ");
     graph.dfs();
  }
}

ڪنسول آئوٽ: جيئن ته اسان وٽ هڪ ويجهڙائي وارو ميٽرڪس آهي ۽ هڪ لوپ اندر هڪ لوپ استعمال ڪري رهيا آهيون، وقت جي پيچيدگي O (N²) هوندي.

بيڊٿ- پھرين ڳولا

کوٽائي-پهريون ڳولا وانگر، هي الگورتھم هڪ آسان ۽ بنيادي گراف ٽرورسل طريقن مان هڪ آهي. خلاصو اهو آهي ته اسان وٽ ڪجهه موجوده ويڪر آهي. اسان ان جي سڀني اڻ ڏٺل ڀرپاسي وارين چوڪن کي قطار ۾ رکون ٿا ۽ ايندڙ عنصر کي چونڊيو (جيڪو قطار جي مٿو تي محفوظ ٿيل ويڪرڪس آهي)، جيڪو موجوده ورٽيڪس بڻجي وڃي ٿو... هن الگورتھم کي مرحلن ۾ ٽوڙڻ سان، اسان هيٺين مرحلن کي سڃاڻي سگھون ٿا:

1. دورو ڪريو اڳئين اڻ ڏٺل ويڙھيءَ جو دورو ڪريو موجوده عمدي جي ڀرسان، ان کي نشان لڳايو جيئن اڳ ۾ ڏٺو ويو، ۽ ان کي قطار ۾ شامل ڪريو.
2. جيڪڏهن قدم # 1 تي عمل نه ٿو ڪري سگھجي، ته پوءِ قطار مان عمودي کي هٽايو ۽ ان کي موجوده عمودي ٺاهيو.
3. جيڪڏهن قدم # 1 ۽ # 2 تي عمل نه ٿو ڪري سگھجي، ته پوءِ اسان ٽرورسنگ ڪريون ٿا - ھر عمدي کي پار ڪيو ويو آھي (جيڪڏھن اسان وٽ ھڪڙو ڳنڍيل گراف آھي).

هتي گراف ڪلاس لڳ ڀڳ هڪجهڙائي آهي جنهن کي اسان استعمال ڪيو ڊيپٿ-فرسٽ سرچ الورورٿم لاءِ، سواءِ سرچ جي طريقي جي پاڻ ۽ حقيقت اها آهي ته قطار اندروني اسٽيڪ کي تبديل ڪري ٿي:

public class Graph {
  private final int MAX_VERTS = 10;
  private Vertex vertexList[]; // Array of vertices
  private int adjMat[][]; // Adjacency matrix
  private int nVerts; // Current number of vertices
  private Queue queue;

  public Graph() {
     vertexList = new Vertex[MAX_VERTS];
     adjMat = new int[MAX_VERTS][MAX_VERTS];
     nVerts = 0;
     for (int j = 0; j < MAX_VERTS; j++) {
        for (int k = 0; k < MAX_VERTS; k++) {  // Fill the adjacency matrix with zeros
           adjMat[j][k] = 0;
        }
     }
     queue = new PriorityQueue<>();
  }

  public void addVertex(char lab) {
     vertexList[nVerts++] = new Vertex(lab);
  }

  public void addEdge(int start, int end) {
     adjMat[start][end] = 1;
     adjMat[end][start] = 1;
  }

  public void displayVertex(int v) {
     System.out.println(vertexList[v].getLabel());
  }

  public void bfc() { // Depth-first search
     vertexList[0].setVisited(true);
     displayVertex(0);
     queue.add(0);
     int v2;

     while (!queue.isEmpty()) {
        int v = queue.remove();

        while((v2 = getAdjUnvisitedVertex(v))!=-1) {// The loop runs until every adjacent vertex is found and added to the queue
           vertexList[v2].visited = true;
           displayVertex(v2);
           queue.add(v2);
        }
     }

     for (int j = 0; j < nVerts; j++) {  // Reset the flags
        vertexList[j].visited = false;
     }

  }

  private int getAdjUnvisitedVertex(int v) {
     for (int j = 0; j < nVerts; j++) {
        if (adjMat[v][j] == 1 && vertexList[j].visited == false) {
           return j; // Returns the first vertext found
        }
     }
     return -1;
  }
}

Vertex ڪلاس هڪجهڙائي آهي جيڪو اسان استعمال ڪيو آهي ڊيپٿ فرسٽ سرچ الگورٿم سان. اچو ته هن الگورتھم کي عمل ۾ رکون:

public class Solution {
  public static void main(String[] args) {
     Graph graph = new Graph();
     graph.addVertex('A'); //0
     graph.addVertex('B'); //1
     graph.addVertex('C'); //2
     graph.addVertex('D'); //3
     graph.addVertex('E'); //4
     graph.addVertex('F'); //5
     graph.addVertex('G'); //6

     graph.addEdge(0,1);
     graph.addEdge(0,2);
     graph.addEdge(0,3);
     graph.addEdge(1,4);
     graph.addEdge(3,5);
     graph.addEdge(5,6);

     System.out.println("Visits: ");
     graph.bfc();
  }
}

ڪنسول آئوٽ: ٻيهر: اسان وٽ هڪ ويجهڙائي وارو ميٽرڪس آهي ۽ هڪ لوپ اندر اندر ٺهيل لوپ استعمال ڪريو، تنهنڪري مٿين الگورتھم جي وقت جي پيچيدگي O (N²) آهي.

4. Dijkstra جي الگورتھم

جيئن اڳ ذڪر ڪيو ويو آهي، گراف کي هدايت يا اڻ سڌي طرح ٿي سگهي ٿو. ۽ توهان کي ياد ڪندو ته اهي به وزن ڪري سگهجي ٿو. وزني، ھدايت ڪيل گراف ماڊل رشتا اڪثر ڪري حقيقي زندگي ۾ ملن ٿا: مثال طور، شھرن جو نقشو جتي شھر چوڪيدار آھن، ۽ انھن جي وچ ۾ ڪنارا آھن روڊ آھن ھڪڙي طرفي ٽرئفڪ سان، ھلندڙ ھلندڙ ڪنڊ جي طرف ھلندڙ. اچو ته چئو ته توهان هڪ مال بردار ڪمپني آهيو ۽ توهان کي ٻن ڏورانهن شهرن جي وچ ۾ ننڍو رستو ڳولڻو پوندو. توهان اهو ڪيئن ڪندا؟ ٻن عمودين جي وچ ۾ ننڍو رستو ڳولڻ ھڪڙو عام مسئلن مان ھڪڙو آھي جيڪو وزن وارا گراف استعمال ڪندي حل ڪيو ويو آھي. هن مسئلي کي حل ڪرڻ لاء، اسان استعمال ڪندا آهيون Dijkstra جي الگورتھم. هڪ دفعو توهان ان کي هلائيندا آهيو توهان کي خبر پوندي ته مختصر ترين رستا ڏنل ابتدائي ورڪس کان هر ٻئي تائين. هن الگورتھم جا مرحلا ڪهڙا آهن؟ مان هن سوال جو جواب ڏيڻ جي ڪوشش ڪندس. Dijkstra جي الگورتھم جا مرحلا:

• قدم 1: ويجھي نوڊ ڳولھيو جنھن کي نيويگيٽ ڪرڻ لاءِ گھٽ ۾ گھٽ قيمت آھي (سڀ کان گھٽ وزن). توھان بلڪل شروعات ۾ بيٺا آھيو ۽ سوچي رھيا آھيو ته ڪيڏانهن وڃڻو آھي: نوڊ A يا نوڊ B ڏانھن. انھن نوڊس مان ھر ھڪ ڏانھن وڃڻ جي قيمت ڇا آھي؟
• قدم 2: نوڊ В جي سڀني پاڙيسرين ڏانهن سفر ڪرڻ لاءِ فاصلو ڳڻيو جيڪي اڃا تائين الورورٿم نه ويا آهن جڏهن В کان ڪنڊ کي پار ڪندي. جيڪڏهن نئون فاصلو پراڻي فاصلي کان گهٽ آهي، ته پوءِ ايج B ذريعي رستو هن ويڪر لاءِ نئون ننڍو رستو بڻجي ويندو.
• مرحلا 3: نشان لڳايو ويٽيڪڪس B کي جيئن دورو ڪيو ويو.
• قدم 4: قدم 1 ڏانھن وڃو.

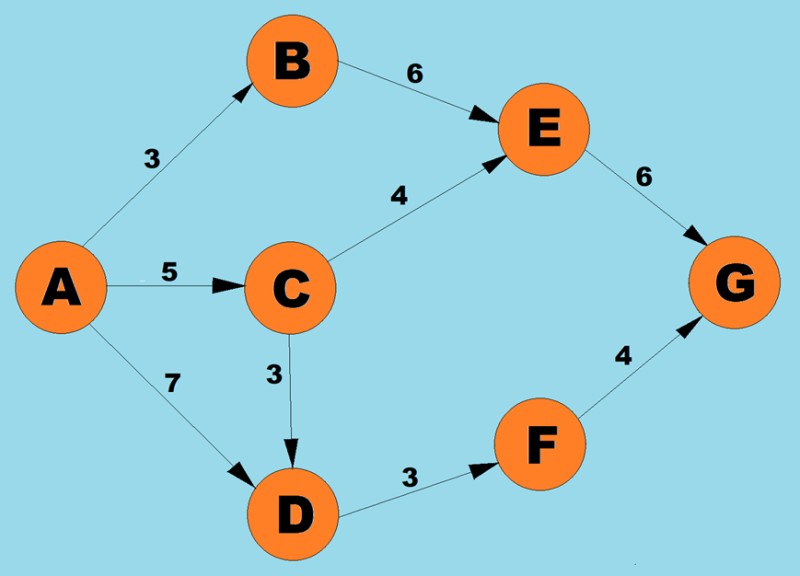اسان انهن قدمن کي هڪ لوپ ۾ ورجائينداسين جيستائين سڀني عمودي جو دورو نه ڪيو وڃي. اچو ته ھيٺ ڏنل وزن واري ھدايت واري گراف تي غور ڪريون: مٿين الگورتھم کي استعمال ڪندي، اسين A کان G تائين ننڍو رستو طئي ڪنداسين.

1. ويرٽيڪس A لاءِ ٽي ممڪن رستا آهن: وزن 3 سان B تائين، وزن 5 سان С، ۽ وزن 7 سان ڊي تائين. الگورٿم جي پهرين مرحلي مطابق، اسان نوڊ کي چونڊون ٿا گھٽ ۾ گھٽ قيمت (ڪنارن جو وزن). هن معاملي ۾، B.

2. جيئن ته B جو واحد اڻ ڏٺل پاڙيسري vertex Е آهي، اسان چيڪ ڪريون ٿا ته رستو ڪهڙو هوندو جيڪڏهن اسان هن ويڪر مان گذرياسين. 3(AB) + 6(BE) = 9.

   ان ڪري، اسان رڪارڊ ڪريون ٿا ته موجوده ننڍو رستو A کان E تائين 9 آهي.

3. جيئن ته اسان جو ڪم vertex B سان مڪمل ٿي چڪو آهي، اسان اڳتي وڌون ٿا ته ايندڙ ويڪرڪس کي چونڊيو جنهن جي ڪنڊ جو وزن گهٽ ۾ گهٽ آهي.

   عمودي A ۽ B کان، امڪان آهن عمودي ڊي (7)، سي (5)، يا اي (6).

   С ڏانهن کنڊ جو تمام ننڍڙو وزن آهي، تنهنڪري اسان هن ويڪر ڏانهن وڃون ٿا.

4. اڳيون، اڳي وانگر، اسان پاڙيسري عمودي ڏانهن ننڍو رستو ڳوليندا آهيون جڏهن C کان لنگهندا آهيون:

   • AD = 5 (AC) + 3 (CD) = 8، پر جيئن ته اڳوڻو ننڍو رستو (AC = 7) هن رستي کان С کان گهٽ آهي، اسان ننڍو رستو رکون ٿا (AC = 7) اڻ تبديل ٿيل.

   • CE = 5(AC) + 4(CE) = 9. هي نئون ننڍو رستو اڳئين رستي جي برابر آهي، تنهنڪري اسان ان کي به اڻ مٽائي ڇڏيون ٿا.

5. ويجھي پهچندڙ چوڪن (E ۽ D) مان، سڀ کان ننڍي کنڊ جي وزن سان عمودي کي چونڊيو، يعني ڊي (3).

6. اسان ان جي پاڙيسري F ڏانهن ننڍو رستو ڳوليندا آهيون.

   AF = 7(AD) + 3(DF) = 9

7. ويجھي پهچندڙ چوڪن (E ۽ F) مان، ننڍي کنڊ جي وزن سان عمودي کي چونڊيو، يعني F (3).

8. ان جي پاڙيسري G ڏانهن ننڍو رستو ڳوليو.

   AG = 7(AD) + 3(DF) + 4(FG) = 14

   تنهن ڪري، اسان هڪ رستو ڳولي ورتو آهي A کان G تائين.

   پر پڪ ڪرڻ لاءِ ته اهو ننڍو آهي، اسان کي به اسان جا قدم عمدي E تي ڪرڻ گهرجن.

9. ڇاڪاڻ ته vertex G وٽ ڪو به پاڙيسري عمودي نه آهي جنهن ڏانهن هدايت ٿيل ڪنڊن ڏانهن اشارو ڪيو ويو آهي، اسان وٽ صرف vertex E ڇڏي ويو آهي، تنهنڪري اسان ان کي چونڊيو.

10. پاڙيسري G ڏانهن ننڍو رستو ڳوليو.

    AG = 3 (AB) + 6 (BE) + 6 (EG) = 15. ھي رستو اڳئين مختصر ترين رستي (AG (14)) کان ڊگھو آھي، تنھنڪري اسان ھن رستي کي اڻڄاڻائي ڇڏيون ٿا.

    جيئن ته G مان نڪرندڙ ڪو به عمودي نه آهي، اهو ڪو به احساس نٿو رکي ته قدمن کي هلائڻ لاء الورورٿم تي هن ويڪر تي. مطلب ته الورورٿم جو ڪم پورو ٿي چڪو آهي.

جيئن مون اڳ ۾ چيو آهي، AG لاءِ مختصر ترين رستو ڳولڻ کان علاوه، اسان vertex A کان هر ٻئي vertex (AB, AC, AD, AE, AF) تائين مختصر ترين رستا پڻ حاصل ڪيا. خير، هاڻي اهو وقت آهي هڪ نظر وٺو ته اهو ڪيئن ٿي سگهي ٿو جاوا ۾. اچو ته ورڪس ڪلاس سان شروع ڪريون:

public class Vertex {
   private char label;
   private boolean isInTree;

   public Vertex(char label) {
       this.label = label;
       this.isInTree = false;
   }

   public char getLabel() {
       return label;
   }

   public void setLabel(char label) {
       this.label = label;
   }

   public boolean isInTree() {
       return isInTree;
   }

   public void setInTree(boolean inTree) {
       isInTree = inTree;
   }
}

vertex ڪلاس لڳ ڀڳ هڪجهڙائي آهي vertex ڪلاس لاءِ استعمال ڪيو ويندو آهي breadth-first search. مختصر ترين رستا ڏيکارڻ لاءِ، اسان کي ھڪ نئين ڪلاس جي ضرورت آھي جنھن ۾ اسان کي گهربل ڊيٽا ھوندي:

public class Path { // A class that contains the distance and the previous and traversed vertices
   private int distance; // Current distance from the starting vertex
   private List parentVertices; // Current parent vertex

   public Path(int distance) {
       this.distance = distance;
       this.parentVertices = new ArrayList<>();
   }

   public int getDistance() {
       return distance;
   }

   public void setDistance(int distance) {
       this.distance = distance;
   }

   public List getParentVertices() {
       return parentVertices;
   }

   public void setParentVertices(List parentVertices) {
       this.parentVertices = parentVertices;
   }
}

هن ڪلاس ۾، اسان رستي جي ڪل فاصلي ۽ چوٽيءَ کي ڏسي سگھون ٿا جيڪي ننڍي کان ننڍي رستي تي گذرڻ وقت گذريا ويندا. ۽ ھاڻي اچو ته ڪلاس کي ڏسون جتي اسان اصل ۾ گراف ذريعي مختصر ترين رستو پار ڪندا آھيون. تنهنڪري هتي اسان وٽ گراف ڪلاس آهي:

public class Graph {
   private final int MAX_VERTS = 10;// Maximum number of vertices
   private final int INFINITY = 100000000; // This number represents infinity
   private Vertex vertexList[]; // List of vertices
   private int relationMatrix[][]; // Matrix of edges between vertices
   private int numberOfVertices; // Current number of vertices
   private int numberOfVerticesInTree; // Number of visited vertices in the tree
   private List shortestPaths; // List of shortest paths
   private int currentVertex; // Current vertex
   private int startToCurrent; // Distance to currentVertex

   public Graph() {
       vertexList = new Vertex[MAX_VERTS]; // Adjacency matrix
       relationMatrix = new int[MAX_VERTS][MAX_VERTS];
       numberOfVertices = 0;
       numberOfVerticesInTree = 0;
       for (int i = 0; i < MAX_VERTS; i++) { // Fill the adjacency matrix
           for (int k = 0; k < MAX_VERTS; k++) { // with "infinity"
               relationMatrix[i][k] = INFINITY; // Assign default values
               shortestPaths = new ArrayList<>(); // Assign an empty list
           }
       }
   }

   public void addVertex(char lab) {// Assign new vertices
       vertexList[numberOfVertices++] = new Vertex(lab);
   }

   public void addEdge(int start, int end, int weight) {
       relationMatrix[start][end] = weight; // Set weighted edges between vertices
   }

   public void path() { // Choose the shortest path
       // Set the initial vertex data
       int startTree = 0; // Start from vertex 0
       vertexList[startTree].setInTree(true); // Include the first element in the tree
       numberOfVerticesInTree = 1;

       // Fill out the shortest paths for vertices adjacent to the initial vertex
       for (int i = 0; i < numberOfVertices; i++) {
           int tempDist = relationMatrix[startTree][i];
           Path path = new Path(tempDist);
           path.getParentVertices().add(0);// The starting vertex will always be a parent vertex
           shortestPaths.add(path);
       }
       // Until every vertex is in the tree
       while (numberOfVerticesInTree < numberOfVertices) { // Do this until the number of of vertices in the tree equals the total number of vertices
           int indexMin = getMin();// Get the index of the of the vertex with the smallest distance from the vertices not yet in the tree
           int minDist = shortestPaths.get(indexMin).getDistance(); // Minimum distance to the vertices not yet in the tree

           if (minDist == INFINITY) {
               System.out.println("The graph has an unreachable vertex");
               break; // If only unreachable vertices have not been visited, then we exit the loop
           } else {
               currentVertex = indexMin; // Set currentVert to the index of the current vertex
               startToCurrent = shortestPaths.get(indexMin).getDistance(); // Set the distance to the current vertex
           }

           vertexList[currentVertex].setInTree(true);  // Add the current vertex to the tree
           numberOfVerticesInTree++; // Increase the count of vertices in the tree
           updateShortestPaths(); // Update the list of shortest paths
       }

       displayPaths(); // Display the results on the console
   }

   public void clear() { // Clear the tree
       numberOfVerticesInTree = 0;
       for (int i = 0; i < numberOfVertices; i++) {
           vertexList[i].setInTree(false);
       }
   }

   private int getMin() {
       int minDist = INFINITY; // The distance of the initial shortest path is taken to be infinite
       int indexMin = 0;
       for (int i = 1; i < numberOfVertices; i++) { // For each vertex
           if (!vertexList[i].isInTree() && shortestPaths.get(i).getDistance() < minDist) { // If the vertex is not yet in the tree and the distance to the vertex is less than the current minimum
               minDist = shortestPaths.get(i).getDistance(); // then update the minimum
               indexMin = i; // Update the index of the vertex with the minimum distance
           }
       }
       return indexMin; // Returns the index of the vertex with the smallest distance among those not yet in the tree
   }

   private void updateShortestPaths() {
       int vertexIndex = 1; // The initial vertex is skipped
       while (vertexIndex < numberOfVertices) { // Run over the columns

           if (vertexList[vertexIndex].isInTree()) { // If the column vertex is already in the tree, then we skip it
               vertexIndex++;
               continue;
           }
           // Calculate the distance for one element sPath
           // Get the edge from currentVert to column
           int currentToFringe = relationMatrix[currentVertex][vertexIndex];
           // Add up all the distances
           int startToFringe = startToCurrent + currentToFringe;
           // Determine the distance to the current vertexIndex
           int shortPathDistance = shortestPaths.get(vertexIndex).getDistance();

           // Compare the distance through currentVertex with the current distance in the vertex with index vertexIndex
           if (startToFringe < shortPathDistance) { // If it is smaller, then the vertex at vertexIndex is assigned the new shortest path
               List newParents = new ArrayList<>(shortestPaths.get(currentVertex).getParentVertices()); // Create a copy of the list of vertices of vertex currentVert's parents
               newParents.add(currentVertex); // And add currentVertex to it as the previous vertex
               shortestPaths.get(vertexIndex).setParentVertices(newParents); // Save the new path
               shortestPaths.get(vertexIndex).setDistance(startToFringe); // Save the new distance
           }
           vertexIndex++;
       }
   }

   private void displayPaths() { // A method for displaying the shortest paths on the screen
       for (int i = 0; i < numberOfVertices; i++) {
           System.out.print(vertexList[i].getLabel() + " = ");
           if (shortestPaths.get(i).getDistance() == INFINITY) {
               System.out.println("0");
           } else {
               String result = shortestPaths.get(i).getDistance() + " (";
               List parents = shortestPaths.get(i).getParentVertices();
               for (int j = 0; j < parents.size(); j++) {
                   result += vertexList[parents.get(j)].getLabel() + " -> ";
               }
               System.out.println(result + vertexList[i].getLabel() + ")");
           }
       }
   }
}

تنهن ڪري اهو سڀ جادو آهي =) هاڻي، اچو ته عمل ۾ هن الگورتھم تي هڪ نظر رکون:

public class Solution {

   public static void main(String[] args) {
       Graph graph = new Graph();
       graph.addVertex('A');
       graph.addVertex('B');
       graph.addVertex('C');
       graph.addVertex('D');
       graph.addVertex('E');
       graph.addVertex('F');
       graph.addVertex('G');

       graph.addEdge(0, 1, 3);
       graph.addEdge(0, 2, 5);
       graph.addEdge(0, 3, 7);
       graph.addEdge(1, 4, 6);
       graph.addEdge(2, 4, 4);
       graph.addEdge(2, 3, 3);
       graph.addEdge(3, 5, 3);
       graph.addEdge(4, 6, 6);
       graph.addEdge(5, 6, 4);

       System.out.println("The following nodes form the shortest paths from node A:");
       graph.path();
       graph.clear();
   }
}

۽ ڪنسول جي پيداوار هي آهي: هن الورورٿم جي وقت جي پيچيدگي O(N²) کان سواءِ ٻيو ڪو به ناهي، ڇو ته اسان وٽ لوپس (Nested loops) آهن. اهو سڀ ڪجهه اڄ مون وٽ آهي. اوهان جي توجه جي مهرباني!