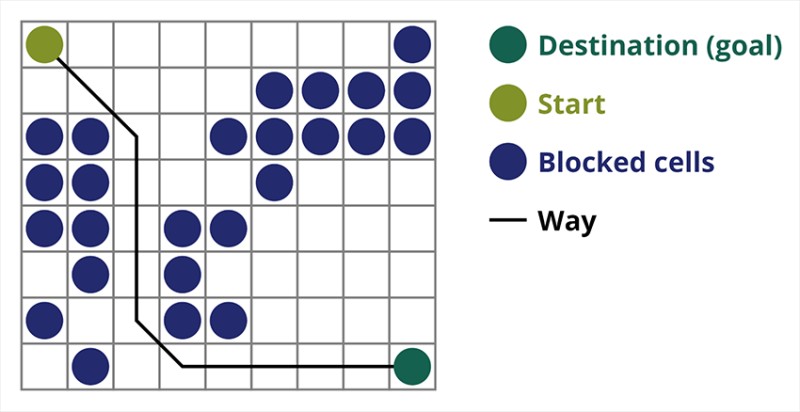
مختلف ڳولا الگورتھم مختلف ڪمن لاءِ ٺھيل آھن. اڄ اسان A* ڳولها بابت ڳالهائڻ وارا آهيون، هڪ تمام مؤثر رستو ڳولڻ وارو الگورتھم. هي هڪ تمام سٺو آهي ڪمپيوٽر گيمز لاءِ ۽ ڳولا جا گراف ٺاهڻ جهڙوڪ شهرن جي وچ ۾ طريقا وغيره. توهان شايد محسوس ڪيو هوندو، مثال طور، اسٽريٽجڪ يا تاکتياتي وڊيو گيمز ۾، ڪيئن هڪ بٽڻ کي دٻائڻ کان پوءِ، توهان جو رانديگر يا گروهه فوري طور تي شروع ٿئي ٿو بغير ڪنهن دير جي فيلڊ پار ڪرڻ لاءِ توهان جي بيان ڪيل نقطي تي. هتي ڪا به دير نه آهي خاص طور تي ڇو ته رانديون موثر الگورتھم استعمال ڪن ٿيون جيڪي حساب ڪن ٿيون ته پليئر کي ڪٿي وڃڻ جي ضرورت آهي. يا هڪ دشمن جيڪو اڻڄاتل طور تي پليئر کي ڳولي ٿو ۽ پري کان صحيح هدايت ۾ هلڻ شروع ڪري ٿو. عام طور تي، A* الورورٿم استعمال ڪيو ويندو آهي اهڙن ڪمن لاءِ.
A* الورورٿم ڇا آهي
Pathfinding algorithm A* هڪ بهترين-پهرين ڳولا الگورٿم جو هڪ مثال آهي. A* الورورٿم جو مقصد هڪ نقطي کان ٻئي تائين رستو ڳولڻ آهي. اهو گراف الگورٿم ڳولڻ لاء ڪلاسن مان هڪ آهي. اچو ته ڄاڻون ته اهو ڪيئن ڪم ڪري ٿو هڪ مثال استعمال ڪندي. تصور ڪريو هڪ 2D راند کي مٿي کان هيٺ ڏسڻ سان. اچو ته اسان جي راند واري علائقي کي چورس لالچ ۾ ورهايو، مثال طور 8*8 سيلز جهڙوڪ شطرنج جي تختي وانگر. اسان جا سيل ٻن قسمن مان هڪ ٿي سگهن ٿا، گذرڻ جي قابل يا ناقابل قابل (رڪيل). هر وقت هڪ پليئر يا دشمن جيڪو پليئر جي ويجهو اچي ٿو هڪ سيل کي منتقل ڪري ٿو. راندين ۾، پاس ڪرڻ وارا سيل مختلف نوعيت جا ٿي سگهن ٿا، مثال طور، هڪ فليٽ روڊ، گھاس يا ريت، جيڪو انهن سان گڏ هلڻ جي تڪليف جو اندازو لڳائي ٿو، پر سادگي لاء اسان اهو فرض ڪنداسين ته سڀئي پاسا سيل سيلز ساڳئي طريقي سان گذري ويا آهن. هيٺ ڏنل تصوير ۾، نيري سيلون رڪاوٽون آهن.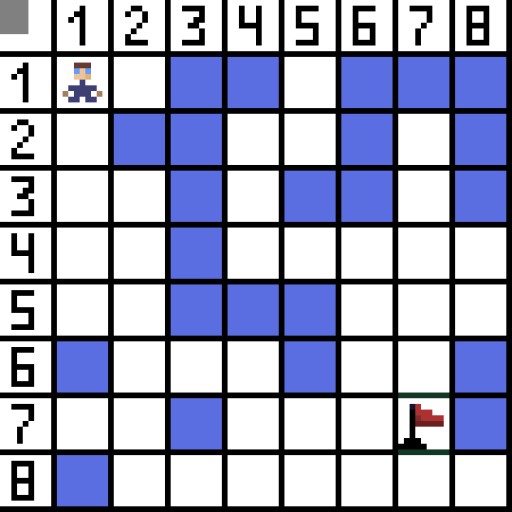
اچو ته ھڪڙي سيل (يا نوڊ) کي شروعاتي سيل جي طور تي تفويض ڪريون (ڪردار ان ۾ آھي)، ۽ ٻئي سيل کي ھدف يا گول سيل (جيڪو جھنڊو آھي)، ۽ بيان ڪريون ته A* الورورٿم ھن ڪيس لاءِ ڪيئن ڪم ڪري ٿو. ڪردار سيل ۾ آهي (1,1) ۽ ٽارگيٽ سيل ۾ آهي (7,7). هر سيل ۾ افقي، عمودي، ۽ ويڪرائي پاڙيسري آهن. اهو منحصر آهي راند تي، جيڪڏهن اسان ڳڻپيوڪر نوڊس يا نه. مثال طور ڪيترن ئي مٿي-ڏسڻ واري راندين ۾ جهڙوڪ Bomberman يا Pacman ڪردار صرف افقي يا عمودي طور تي منتقل ڪري سگهن ٿا. انهي حالت ۾ هر نوڊ، ڪنڊن کي ڇڪڻ کان سواء، صرف 4 پاڙيسري آهن. جيڪڏهن اسان هڪ راند جي باري ۾ ڳالهائي رهيا آهيون جتي ڪردارن کي تري ۾ منتقل ڪري سگهجي ٿو، هر نوڊ کي 8 پاڙيسري تائين ٿي سگهي ٿو. الورورٿم جي پهرين قدم تي، سيل جتي ڪردار واقع آهي ٻه پاڙيسري آهن. وڌيڪ واضح طور تي، ٽي، پر انهن مان هڪ هڪ رڪاوٽ آهي. 
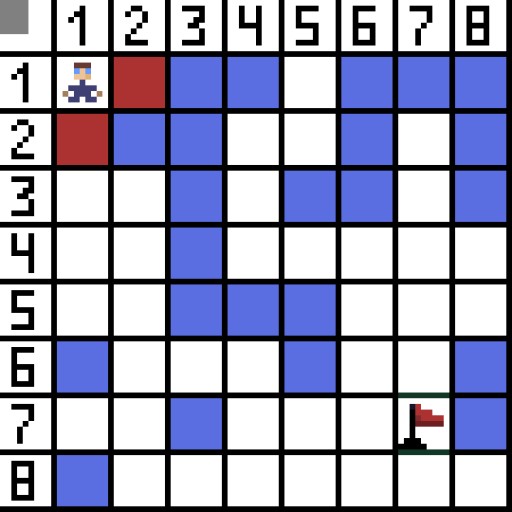اهو واضح آهي ته ويڪرائي طريقو ڊگهو آهي. جيڪڏهن اسان پنهنجي سيل جي پاسن کي شرط طور هڪ جي برابر رکون ٿا، ته پوء هن سيل جي ويڪر جي ڊيگهه ٻن جي چورس روٽ جي برابر آهي. اھو اھو آھي جيڪو پٿگورين جو نظريو چوي ٿو. سيل A کان سيل B تائين حاصل ڪرڻ لاء، توهان کي پهريان پاڙيسري سيلن مان هڪ کي چونڊڻ گهرجي، ۽ پوء ايندڙ هڪ، وغيره. انهي سان گڏ، رستي ۾، سمجھو ته ڇا اهو ممڪن آهي ته شروعاتي سيل کان ٽارگيٽ هڪ تائين. A* الورورٿم هر قدم تي پاڙيسري سيلز مان هڪ کي منتخب ڪري ٿو فنڪشن F جي قدر جي مطابق. هي فنڪشن ماپ ڪري ٿو ته هڪ اميدوار سيل کي اسان جي مختصر ترين رستي ۾ شامل ڪيو وڃي. هي قيمت فنڪشن آهي، ۽ اهو حرڪت فنڪشن G ۽ هوريسٽڪ فنڪشن جو مجموعو آهي.
-
G قيمت - شروعاتي نوڊ کان فاصلو آھي.
-
H قيمت (Heuristic) آخر (مقصد) نوڊ کان فاصلو آھي. هي فنڪشن مختلف ٿي سگهي ٿو، هڪ ڊولپر فيصلو ڪري ٿو ته ڇا بهتر آهي. شايد H جو انتخاب A* ۾ سڀ کان وڌيڪ اهم آهي، ۽ اهو ئي نقطو آهي جيڪو الورورٿم جي ڪنهن خاص عمل کي وڌيڪ يا گهٽ اثرائتو بڻائي ٿو. نظرياتي طور تي توهان ڪنهن به فنڪشن کي استعمال ڪري سگهو ٿا جيڪو توهان چاهيو ٿا.
اسان جي حالت ۾، اسان ٽارگيٽ سيل جي پوزيشن کي ڄاڻون ٿا ۽ مثال طور، ھدف ۽ موجوده سيل جي وچ ۾ جاميٽري ايڪليڊين جي فاصلي کي حساب ڪري سگھون ٿا. جيترو ننڍو فاصلو، اوترو ئي اسان مقصد جي ويجهو آهيون.
-
F لاڳت = G + H. تنهن ڪري الگورٿم سڀني پاڙيسري نوڊس F جي قيمتن کي ڳڻائي ٿو ۽ سڀ کان گھٽ F قيمتن مان ھڪڙو چونڊي ٿو پھريائين ڏسڻ لاءِ. جڏهن اسان هڪ چونڊيو ٿا ته اسان ان کي بند طور نشان لڳايو ۽ هن نوڊ پاڙيسري لاءِ قدر ڳڻيو.
Heuristic function اسان H ڪيئن حساب ڪري سگھون ٿا؟
هي هڪ heuristic فنڪشن آهي. نالو پاڻ جو مطلب آهي ته اهو تجربو طرفان طئي ڪيو ويو آهي، ۽ مختلف ٿي سگهي ٿو. هتي اسان ان کي پوائنٽس (x1, y1) ۽ (x2, y2) جي وچ ۾ نام نهاد ايڪليڊين فاصلي جي برابر کڻنداسين: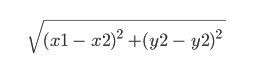
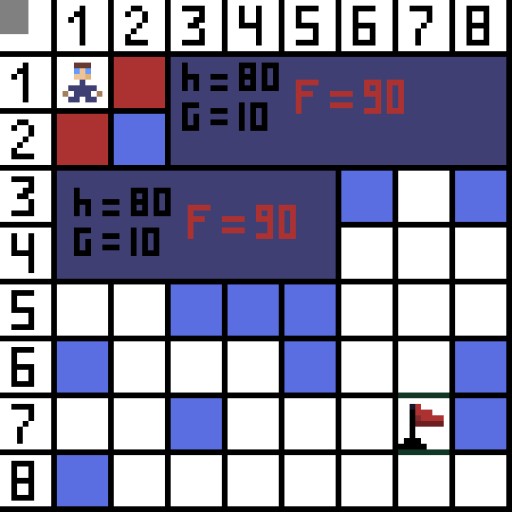تصوير ۾، پهرين قدم لاءِ، ٻه آپشن آهن، ۽ اهي قيمت ۾ ساڳيا آهن، پر ايندڙ قدم تي، ڪردار اختيارن مان هڪ ۾ ختم ٿي ويندو آهي. تنهن ڪري، اسان ٻئي طرف وڃي رهيا آهيون. ايندڙ ورهاڱي ۾، اسان وٽ پهريان ئي 4 آپشن آهن. 
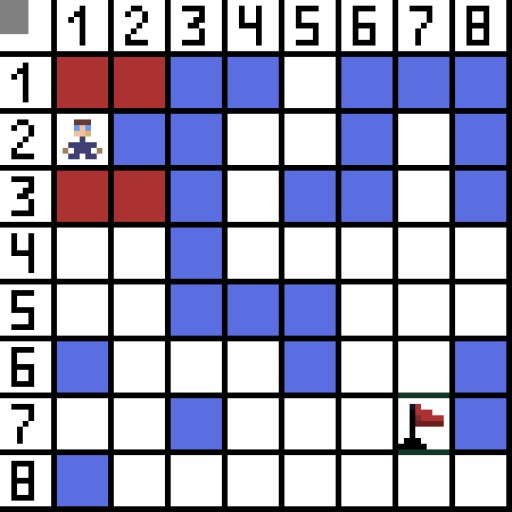انهن مان ٻه مناسب نه آهن، ڇاڪاڻ ته اهي پوئتي موٽندا آهن، ۽ ٻيا اختيار هڪجهڙا سٺا آهن، پر الورورٿم اهو فيصلو ڪيو ته اهو بهتر آهي ته سيل ڏانهن تري ۾ وڃڻ (3,2). وڌيڪ، هر قدم تي، فنڪشن F جي حساب سان بار بار ڪيو ويندو آهي جيستائين ڪردار ٽارگيٽ سيل تائين پهچي. جيڪڏهن، يقينا، اهڙي پاسو موجود آهي. 
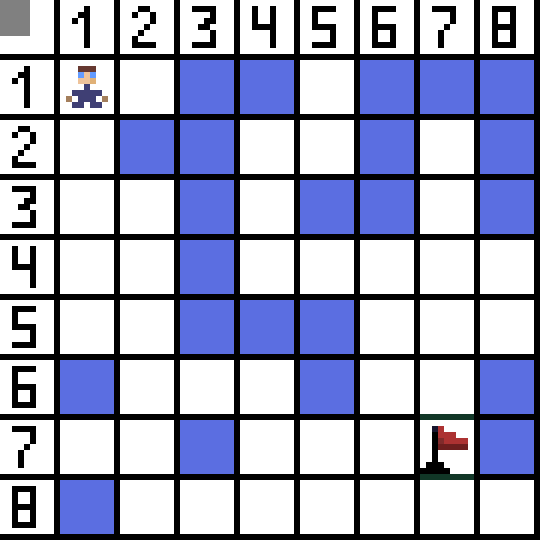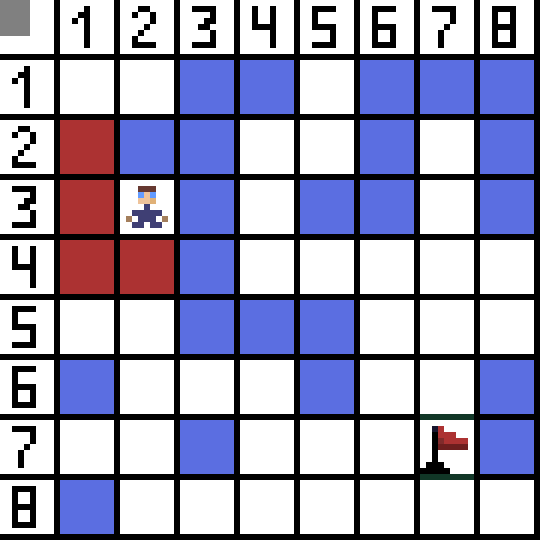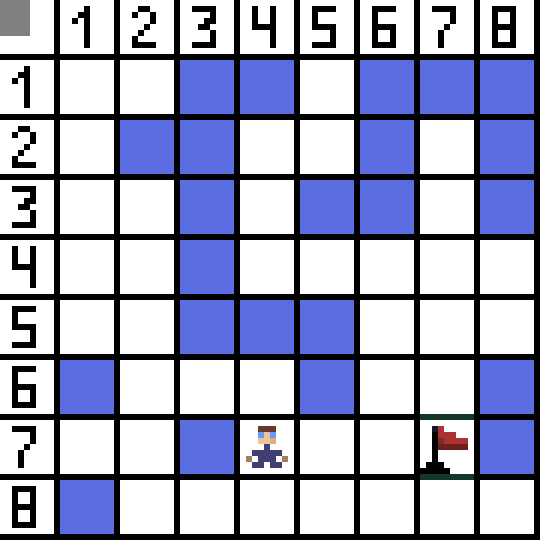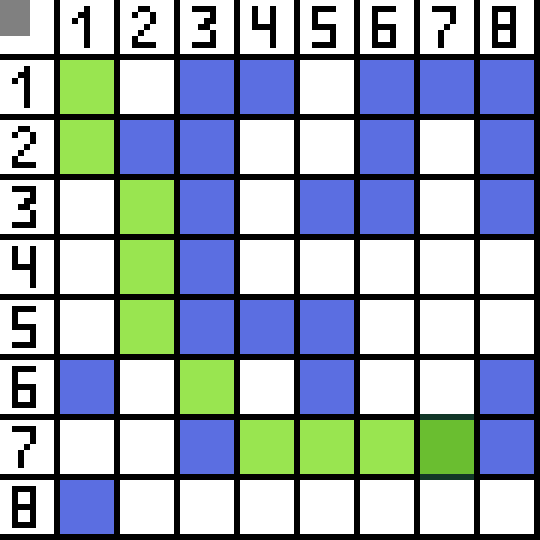گف تصوير تي سائو رستو ڏيکاري ٿو ڪردار جو بهترين رستو پرچم ڏانهن.
A* الگورتھم قدم بہ قدم
جاوا ۾ الگورتھم کي لاڳو ڪرڻ لاءِ، توھان کي ھيٺيان قدم کڻڻا پوندا 1. پھريون توھان کي ٻه لسٽون ٺاھڻ جي ضرورت آھي، کليل نوڊس ۽ بند نوڊس لاءِ. 2. ٻنهي لسٽن کي شروع ڪريو. بند ٿيل لسٽ ۾، شروعاتي نوڊ کليل فهرست ڏانهن اشارو ڪري ٿو. 3. جڏهن ته کليل فهرست ۾ عنصر آهن: 3a. سڀ کان ننڍو F 3b سان نوڊ منٽ ڳوليو. کليل فهرست مان منٽ هٽايو 3c. پاڙيسري منٽ جو اندازو لڳايو (8 تائين، جيڪڏهن ڊاڪٽرن کي حساب ۾ ورتو وڃي) 3d. هر پاڙيسري جي جانچ ڪندي: الف) جيڪڏهن پاڙيسري ٽارگيٽ سيل آهي، ڳولڻ بند ڪريو ب) جيڪڏهن نه، حساب ڪريو G، H ان لاءِ. G = min.G + پاڙيسري ۽ min F = G + H جي وچ ۾ فاصلو) جيڪڏهن نوڊ ساڳئي پوزيشن سان پاڙيسري جي کليل فهرست ۾ آهي ۽ ان جو F پاڙيسري کان گهٽ آهي، ان پاڙيسري کي ڇڏي ڏيو d) جيڪڏهن نوڊ ساڳئي پوزيشن سان پاڙيسري جي بند لسٽ ۾ آهي، ۽ ان جو f پاڙيسري کان گهٽ آهي، ان پاڙيسري کي ڇڏي ڏيو. ٻي صورت ۾، نوڊ کي کليل فهرست ۾ شامل ڪريو اندروني لوپ 3e جي آخر ۾. بند ٿيل لسٽ ۾ منٽ شامل ڪرڻ ٻاهرين لوپ جي آخر ۾، تنهن ڪري، هر دفعي تي اسين اڳتي وڌڻ وارا آهيون:- اسان جي کليل فهرست مان سيل کي منتخب ڪريو گھٽ ۾ گھٽ ڪل اسڪور سان.
- هن سيل کي کليل فهرست مان هٽايو.
- سڀني سيلز کي شامل ڪريو جيڪي اسان ان کان کليل لسٽ ۾ پهچي سگھون ٿا.
- جڏهن اسان اهو ڪريون ٿا، اسان ان نوڊ کان هر نئين نمبر تي نئين سکور کي پروسيس ڪريون ٿا ته ڏسو ته ڇا اهو بهتر آهي جيڪو اسان هن وقت تائين ڪيو آهي، ۽ جيڪڏهن اهو آهي، اسان تازه ڪاري ڪريون ٿا جيڪو اسان ان سيل بابت ڄاڻون ٿا.
A* Pseudocode
هتي A* pathfinding جو مختصر pseudocode آهي:Input: a grid with locked and empty cells, with start and goal cell.
Output: least cost path from start to goal cell.
Initialisation
openList = {startCell} //list of traversed cells
closedList = {} //list of already traversed cells
g.startCell = 0 //cost from source cell to a cell
h.startCell = h(startCell, goal) //heuristic
f.startCell = g.startCell + h.StartCell
while openList is not empty
do
//let the currentCell equal the cell with the least f value
currentCell = Cell on top of openList, with least f
if currentCell == end return
remove currentCell from openList
add currentCell to closedList
foreach n in child.currentCell
if n in closedList
continue
cost = g.currentCell + distance(currentCell,n)
if (n in openList and cost < g.n)
remove n from closedList
g.n = cost
h.n = h(n, goal)
f.n = g.n + h.npseudocode کان A* جاوا ۾ لاڳو ڪرڻ
A* جاوا ريئلائزيشن ۾ پاٿ فائڊنگ کي الورورٿم جي خدمت ڪرڻ لاءِ ڪجهه طريقا هجڻ گهرجن:- سيل، هڪ ڍانچي کي ضروري پيٽرول رکڻ لاء
- کليل ۽ بند فهرستون
- heuristic فنڪشن کي ڳڻڻ جو طريقو
- ذريعو کان منزل تائين رستو ڳولڻ جو طريقو
- چيڪ ڪرڻ جا طريقا ته ڇا ڏنل سيل بلاڪ ٿيل آهي، جيڪڏهن اهو اڳي ئي پهچي چڪو آهي، جيڪڏهن اهو صحيح آهي وغيره.
package Asterist;
import java.util.PriorityQueue;
import java.util.Stack;
public class AAsterisk {
//Java Program to implement A* Search Algorithm
//Here we're creating a shortcut for (int, int) pair
public static class Pair {
int first;
int second;
public Pair(int first, int second){
this.first = first;
this.second = second;
}
@Override
public boolean equals(Object obj) {
return obj instanceof Pair && this.first == ((Pair)obj).first && this.second == ((Pair)obj).second;
}
}
// Creating a shortcut for tuple<int, int, int> type
public static class Details {
double value;
int i;
int j;
public Details(double value, int i, int j) {
this.value = value;
this.i = i;
this.j = j;
}
}
// a Cell (node) structure
public static class Cell {
public Pair parent;
// f = g + h, where h is heuristic
public double f, g, h;
Cell()
{
parent = new Pair(-1, -1);
f = -1;
g = -1;
h = -1;
}
public Cell(Pair parent, double f, double g, double h) {
this.parent = parent;
this.f = f;
this.g = g;
this.h = h;
}
}
// method to check if our cell (row, col) is valid
boolean isValid(int[][] grid, int rows, int cols,
Pair point)
{
if (rows > 0 && cols > 0)
return (point.first >= 0) && (point.first < rows)
&& (point.second >= 0)
&& (point.second < cols);
return false;
}
//is the cell blocked?
boolean isUnBlocked(int[][] grid, int rows, int cols,
Pair point)
{
return isValid(grid, rows, cols, point)
&& grid[point.first][point.second] == 1;
}
//Method to check if destination cell has been already reached
boolean isDestination(Pair position, Pair dest)
{
return position == dest || position.equals(dest);
}
// Method to calculate heuristic function
double calculateHValue(Pair src, Pair dest)
{
return Math.sqrt(Math.pow((src.first - dest.first), 2.0) + Math.pow((src.second - dest.second), 2.0));
}
// Method for tracking the path from source to destination
void tracePath(
Cell[][] cellDetails,
int cols,
int rows,
Pair dest)
{ //A* Search algorithm path
System.out.println("The Path: ");
Stack<Pair> path = new Stack<>();
int row = dest.first;
int col = dest.second;
Pair nextNode = cellDetails[row][col].parent;
do {
path.push(new Pair(row, col));
nextNode = cellDetails[row][col].parent;
row = nextNode.first;
col = nextNode.second;
} while (cellDetails[row][col].parent != nextNode); // until src
while (!path.empty()) {
Pair p = path.peek();
path.pop();
System.out.println("-> (" + p.first + "," + p.second + ") ");
}
}
// A main method, A* Search algorithm to find the shortest path
void aStarSearch(int[][] grid,
int rows,
int cols,
Pair src,
Pair dest)
{
if (!isValid(grid, rows, cols, src)) {
System.out.println("Source is invalid...");
return;
}
if (!isValid(grid, rows, cols, dest)) {
System.out.println("Destination is invalid...");
return;
}
if (!isUnBlocked(grid, rows, cols, src)
|| !isUnBlocked(grid, rows, cols, dest)) {
System.out.println("Source or destination is blocked...");
return;
}
if (isDestination(src, dest)) {
System.out.println("We're already (t)here...");
return;
}
boolean[][] closedList = new boolean[rows][cols];//our closed list
Cell[][] cellDetails = new Cell[rows][cols];
int i, j;
// Initialising of the starting cell
i = src.first;
j = src.second;
cellDetails[i][j] = new Cell();
cellDetails[i][j].f = 0.0;
cellDetails[i][j].g = 0.0;
cellDetails[i][j].h = 0.0;
cellDetails[i][j].parent = new Pair( i, j );
// Creating an open list
PriorityQueue<Details> openList = new PriorityQueue<>((o1, o2) -> (int) Math.round(o1.value - o2.value));
// Put the starting cell on the open list, set f.startCell = 0
openList.add(new Details(0.0, i, j));
while (!openList.isEmpty()) {
Details p = openList.peek();
// Add to the closed list
i = p.i; // second element of tuple
j = p.j; // third element of tuple
// Remove from the open list
openList.poll();
closedList[i][j] = true;
// Generating all the 8 neighbors of the cell
for (int addX = -1; addX <= 1; addX++) {
for (int addY = -1; addY <= 1; addY++) {
Pair neighbour = new Pair(i + addX, j + addY);
if (isValid(grid, rows, cols, neighbour)) {
if(cellDetails[neighbour.first] == null){ cellDetails[neighbour.first] = new Cell[cols]; }
if (cellDetails[neighbour.first][neighbour.second] == null) {
cellDetails[neighbour.first][neighbour.second] = new Cell();
}
if (isDestination(neighbour, dest)) {
cellDetails[neighbour.first][neighbour.second].parent = new Pair ( i, j );
System.out.println("The destination cell is found");
tracePath(cellDetails, rows, cols, dest);
return;
}
else if (!closedList[neighbour.first][neighbour.second]
&& isUnBlocked(grid, rows, cols, neighbour)) {
double gNew, hNew, fNew;
gNew = cellDetails[i][j].g + 1.0;
hNew = calculateHValue(neighbour, dest);
fNew = gNew + hNew;
if (cellDetails[neighbour.first][neighbour.second].f == -1
|| cellDetails[neighbour.first][neighbour.second].f > fNew) {
openList.add(new Details(fNew, neighbour.first, neighbour.second));
// Update the details of this
// cell
cellDetails[neighbour.first][neighbour.second].g = gNew;
//heuristic function cellDetails[neighbour.first][neighbour.second].h = hNew;
cellDetails[neighbour.first][neighbour.second].f = fNew;
cellDetails[neighbour.first][neighbour.second].parent = new Pair( i, j );
}
}
}
}
}
}
System.out.println("Failed to find the Destination Cell");
}
// test
public static void main(String[] args) {
//0: The cell is blocked
// 1: The cell is not blocked
int[][] grid = {
{ 1, 1, 0, 0, 1, 0, 0, 0 },
{ 1, 0, 0, 1, 1, 0, 1, 0 },
{ 1, 1, 0, 1, 0, 0, 1, 0 },
{ 1, 1, 0, 1, 1, 1, 1, 1 },
{ 1, 1, 0, 0, 0, 1, 1, 1 },
{ 0, 1, 1, 1, 0, 1, 1, 0 },
{ 1, 1, 0, 1, 1, 1, 1, 0 },
{ 0, 1, 1, 1, 1, 1, 1, 1 }
};
// Start is the left-most upper-most corner
Pair src = new Pair(0,0);
//(8, 0);
// Destination is the right-most bottom-most corner
Pair dest = new Pair(6, 6);
AAsterisk app = new AAsterisk();
app.aStarSearch(grid, grid.length , grid[0].length, src, dest);
}
}
رستو: -> (0,0) -> (1,0) -> (2,1) -> (3,1) -> (4,1) -> (5,2) -> (5, 3) -> (6,4) -> (6,5) -> (6,6)
اهو ڏسي سگھجي ٿو ته اهو ڪيترن ئي مختصر ترين رستن مان هڪ آهي جيڪو انهن ٻن پوائنٽن جي وچ ۾ تعمير ڪري سگهجي ٿو. ياد رهي ته ڇهين قدم اسان جي مثال ۾ تصوير ۾ ۽ پروگرام جي پيداوار ۾ مختلف آهي، جيتوڻيڪ رستا هڪجهڙائي اثرائتو ٿي چڪا آهن. پروگرام ڪيترن ئي موثر اختيارن مان هڪ چونڊيندو آهي.
GO TO FULL VERSION