جاوا میں میکس ہیپ

بائنری درخت

جاوا میں، ڈیٹا ڈھانچے کی بہت سی مختلف اقسام ہیں۔ ڈھیر درخت کی ساخت پر مبنی ہے جسے بائنری ٹری کہتے ہیں ۔ ایک بائنری ٹری نوڈس پر مشتمل ہوتا ہے، جن میں سے ہر ایک میں زیادہ سے زیادہ 2 چائلڈ نوڈس ہوسکتے ہیں: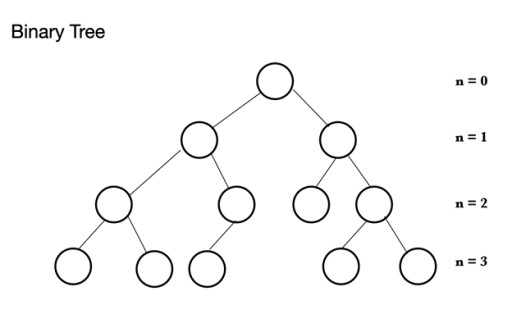 ایک بائنری ٹری پیرنٹ نوڈ پر مشتمل ہوتا ہے جس میں 0 سے 2 نوڈس ہوسکتے ہیں۔ اس میں لیفٹ چائلڈ نوڈ اور/یا رائٹ چائلڈ نوڈ ہو سکتا ہے، یا بالکل بھی کوئی نوڈ نہیں ہو سکتا۔ ایک مکمل بائنری ٹری میں، تمام نوڈس بھرے ہوتے ہیں سوائے آخری سطح کے جو کہ بھرا ہو سکتا ہے، لیکن اسے بھرنے کی ضرورت نہیں ہے۔ آخری سطح، نویں سطح میں 1 سے 2n نوڈس ہو سکتے ہیں، جہاں پہلا n = 0 پر ہے اور جڑ ہے۔

زیادہ سے زیادہ ڈھیر

میکس ہیپ (یا میکس ہیپ) ایک مکمل بائنری ٹری ہے ۔ اس کے بارے میں اہم بات یہ ہے کہ پیرنٹ نوڈ کی قدر لیفٹ اور رائٹ چائلڈ نوڈس سے زیادہ یا اس کے برابر ہونی چاہیے۔ اگر اس پر عمل نہیں کیا جاتا ہے، تو آپ کے پاس زیادہ سے زیادہ ہیپ نہیں ہے۔ کم ہیپ، دوسری طرف، جڑ کے برعکس ہے کیونکہ سب سے چھوٹی قدر یکے بعد دیگرے نوڈس کی قدر میں بڑھ رہی ہے۔ ہر چائلڈ نوڈ کی قدر اس کے والدین سے زیادہ یا اس کے برابر ہوتی ہے۔ یہ ایک مکمل بائنری درخت بھی ہے۔ زیادہ سے زیادہ ہیپ کی ایک مثال یہ ہے: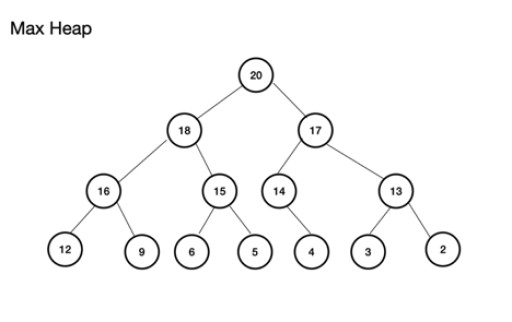 زیادہ سے زیادہ ہیپ ایک صف سے بنایا جا سکتا ہے۔ اس صف کے بارے میں ایک درخت کے لحاظ سے سوچا جائے گا۔ ایک ہیپ کے لیے، اگر جڑ، (درخت کا سب سے اوپر پیرنٹ نوڈ) پوزیشن (انڈیکس) n پر ذخیرہ کیا جاتا ہے، تو اس کی تعریف array، theArray کے لیے کی جاتی ہے ، بطور theArray[n] ۔ لیفٹ اور رائٹ چائلڈ نوڈز بالترتیب theArray [2n+1] اور theArray[2n+2] پر ہیں۔ زیادہ سے زیادہ ہیپ کے لیے، جڑ array[0] پر ہے ۔ لیول n کے لیے، روٹ n = 0: theArr[n] پیرنٹ نوڈ ہے theArr[(2*n)+1] بائیں چائلڈ نوڈ ہے TheArr[(2*n)+2] دائیں چائلڈ نوڈ ہے۔

ترجیحی قطار کی کلاس

جاوا میں ہیپس کو PriorityQueue کلاس کا استعمال کرتے ہوئے لاگو کیا جا سکتا ہے۔ ترجیحی قطاروں کا استعمال کسی مجموعہ میں سب سے زیادہ یا کم از کم اہم شے تلاش کرنے کے لیے کیا جاتا ہے۔ PriorityQueue کلاس java.util.package میں مل سکتی ہے ۔ ترجیحی قطاریں ایسی اشیاء سے بنائی جانی چاہئیں جن کا موازنہ کیا جا سکے تاکہ انہیں قطار میں ایک خاص ترتیب میں رکھا جائے۔ PriorityQueue میں موازنہ کرنے والا ہو سکتا ہے تاکہ اشیاء کے درمیان موازنہ کیا جائے اور اس موازنہ کے مطابق قطار بنائی جائے۔ ایک مثال یہ ہے:

import java.util.Comparator;
import java.util.PriorityQueue;

public class Main
{
    public static void main(String[] args) {
        // Create PriorityQueue with comparator for ascending order of array length
        PriorityQueue intQueue = new PriorityQueue((a,b) -> a - b);
        Integer [] array1 = {1, 2, 4, 6, 8, 9};
        Integer [] array2 = {3, 6, 9};
        Integer [] array3 = {2, 4, 8, 16, 32, 64, 128};
        Integer [] array4 = {5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55};
        Integer [] array5 = {4};

        //Add the array lengths to intQueue
        intQueue.add(array1.length);
        intQueue.add(array2.length);
        intQueue.add(array3.length);
        intQueue.add(array4.length);
        intQueue.add(array5.length);
        //Write out contents of intQueue as stored
        while (intQueue.size() != 0) {
            System.out.println(intQueue.remove());
        }
    }
}

آؤٹ پٹ دینا: اس مثال میں، intQueue کا ڈیفالٹ سائز 11 ہے، اس لیے بیان نہیں کیا گیا ہے (عام طور پر موازنہ کرنے والے سے پہلے پہلی دلیل) اور comparator کو اس طرح دیا گیا ہے: یہ intQueue میں آئٹمز کے درمیان موازنہ کرے گا اور اسے صعودی ترتیب کی صف کی لمبائی میں ترتیب دے گا۔

زیادہ سے زیادہ ہیپ بنانے کے لیے ترجیحی قطار کا نفاذ

PriorityQueue کلاس بغیر کسی موازنہ کے کم سے کم ہیپ پر ڈیفالٹ ہوتی ہے۔ کم سے کم ہیپ زیادہ سے زیادہ ہیپ کے برعکس ہے اور اس لیے جڑ سب سے چھوٹی قدر ہے اور یکے بعد دیگرے چائلڈ نوڈس جڑ اور اس کے بعد آنے والے پیرنٹل نوڈس کے برابر یا بڑے ہوتے ہیں۔ اس وجہ سے، زیادہ سے زیادہ ہیپ کے لیے، جاوا کے کلیکشن فریم ورک سے reverseOrder() کو بطور موازنہ استعمال کرنا ضروری ہے ۔ یہ یقینی بنائے گا کہ ہمیں زیادہ سے زیادہ ہیپ ملے گا نہ کہ ایک منٹ ہیپ۔ اس کلاس میں مفید طریقے ہیں جیسے add() , contains() , remove() , poll() , اور peek() ۔ عناصر قطار میں شامل کیے جاتے ہیں اور کسی بھی ترتیب میں ہو سکتے ہیں۔ نئی PriorityQueue قطار ان عناصر کو معکوس ترتیب میں زیادہ سے زیادہ ہیپ کے طور پر ذخیرہ کرے گی۔ جب قطار لکھی جائے گی، ترتیب یہ ہو گی: روٹ بائیں بچے کی جڑ کے ساتھ والدین کے طور پر (بائیں بچہ_1) دائیں بچے کی جڑ کے ساتھ والدین کے طور پر (دائیں-بچہ_1) لیفٹ-چائلڈ کے ساتھ لیفٹ-چائلڈ_1 بطور والدین (بائیں بچہ_2) ) دائیں بچے کے ساتھ بائیں بچے_1 بطور والدین (دائیں بچے_2) بائیں بچے کے ساتھ دائیں بچے_1 بطور والدین (بائیں بچے_3) دائیں بچے کے ساتھ دائیں بچے_1 بطور والدین (دائیں بچے_3) بائیں بچے کے ساتھ بائیں بچے_2 بطور والدین (بائیں بچہ_4) دائیں بچے کے ساتھ بائیں بچہ_2 بطور والدین (دائیں بچہ_4) وغیرہ درج ذیل کوڈ اس بات کی ایک مثال ہے کہ جاوا میں میکس ہیپ (میکس ہیپ) کیسے بنایا جاتا ہے۔ ایسا کرنے کا پہلا کام ان اقدار کے ساتھ ایک صف کو بھرنا ہے جس کے لئے زیادہ سے زیادہ ہیپ بنایا جائے گا۔ اسے Array کہتے ہیں ۔ اس کے بعد، ایک ترجیحی قطار ، theQueue ، بنائی جاتی ہے اور پھر Array کے عناصر کو اس میں شامل کیا جاتا ہے۔ یہ طریقہ add() کا استعمال کرتا ہے ، جیسے theQueue.add(10) قطار کے آخر میں 10 شامل کرنے کے لیے۔ PriorityQueue کلاس کی کچھ فعالیت کو واضح کرنے کے لیے ، طریقہ peek() پھر ہیپ کا سر تلاش کرنے کے لیے استعمال کیا جاتا ہے، اور یہ زیادہ سے زیادہ قدر ہے، اس صورت میں، 99۔ اگلا کام ہیپ کے سائز کو چیک کرنا ہے۔ size() کا استعمال کرتے ہوئے جو 9 پایا جاتا ہے اور یہ کنسول پر پرنٹ کیا جاتا ہے۔ میتھڈ رائٹ میکس ہیپ قطار میں موجود عناصر کو روٹ کی ترتیب سے لکھتا ہے، لیفٹ چائلڈ روٹ کے ساتھ بطور والدین، دائیں بچہ روٹ کے ساتھ بطور والدین، لیفٹ چائلڈ پہلے لیفٹ چائلڈ کے ساتھ بطور والدین، دائیں بچے کو پہلے لیفٹ چائلڈ کے ساتھ والدین، دائیں بچے کے ساتھ پہلے دائیں بچے کے بطور والدین، بائیں بچے کے ساتھ پہلے دائیں بچے کے ساتھ والدین وغیرہ PriorityQueue طریقہ کو contains(J) یہ معلوم کرنے کے لیے استعمال کیا جاتا ہے کہ آیا کوئی مخصوص عنصر، J، قطار میں ہے ۔ اس صورت میں ہم J = 10 کو تلاش کرتے ہیں۔ ہماری مثال میں، یہ سچ ہے کہ یہ قطار میں ہے اس لیے کنسول پر یہ سچ لکھا جاتا ہے۔ ایک اور PriorityQueue طریقہ، remove(J) پھر J = 10 کو قطار سے ہٹانے کے لیے استعمال کیا جاتا ہے ۔ PriorityQueue کی مزید فعالیت کو واضح کرنے کے لیے ، میتھڈ پول() کا استعمال ہیڈ ایلیمنٹ (زیادہ سے زیادہ قدر) کو ہٹانے کے لیے کیا جاتا ہے جب کہ تھوڑی دیر کے لوپ کا استعمال کرتے ہوئے، ہر بار نئی قطار میں ہیڈ ایلیمنٹ کو ہٹاتے ہوئے اور ہر بار قطار کے سائز کو ایک ایک کرکے کم کیا جاتا ہے۔ یہ طریقہ رائٹ کیو میں ہوتا ہے جسے مین سے بلایا جاتا ہے۔ ہر بار ہٹائے گئے عنصر کو کنسول پر پرنٹ کیا جاتا ہے۔ اصل قطار میں آخر کار کوئی عنصر باقی نہیں رہے گا۔ طباعت شدہ عناصر قدر کے نزولی ترتیب میں زیادہ سے زیادہ ڈھیر ہیں، جہاں ہر بار قطار کا سر پرنٹ کیا جاتا ہے۔

mport java.util.Collections;
import java.util.PriorityQueue;

public class MaxHeap {

       public static void writeQueue(PriorityQueue<Integer> priorityQueue)
       {
           // Write out elements in queue, priorityQueue, and remove them using poll()
           while(priorityQueue.size() != 0)
           {
               System.out.println(priorityQueue.poll());
           }
       }

       public static void writeMaxHeap(PriorityQueue<Integer> priorityQueue)
       {
           // Write out elements in queue as a max heap - root, left child, right child, etc
           for (Integer element : priorityQueue) {
               System.out.println(element);
           }
       }

       public static void main(String args[])
       {
           // Array of numbers to create a max heap array from
           int[] theArray = {5, 3, 13, 10, 99, 19, 6, 51, 9};

           // theQueue is created
           PriorityQueue<Integer> theQueue =
                   new PriorityQueue<Integer>(Collections.reverseOrder());

           // Elements are added to theQueue
           for (int i = 0 ; i <theArray.length; ++i)
           {
               theQueue.add(theArray[i]);
           }

           // The head or root element (priority element) is printed out
           System.out.println("The root value is : " +  theQueue.peek());

           // Find size of theQueue. Use method size()
           Integer s = theQueue.size();
           System.out.println("Size of theQueue? " + s);

           // All elements of theQueue are printed in terms of parent,
           // left child, right child
           System.out.println("theQueue written using for loop:");
           writeMaxHeap(theQueue);

           // Does theQueue contain 10? Use method contains()
           boolean b = theQueue.contains(10);
           System.out.println("Does theQueue contain 10? " + b);

           // Erasing value 10 from array using remove()
           theQueue.remove(10);

           // All elements of theQueue are printed out and removed.
           // Each one is the maximum value left in the queue.
           // At the end theQueue will be empty
           System.out.println("theQueue written out using poll():");
           writeQueue(theQueue);

           // Find size of theQueue. Use method size()
           s = theQueue.size();
           System.out.println("Size of theQueue? " + s);
       }
   }

آؤٹ پٹ:

Max Heapify

Max Heapify الگورتھم اس بات کو یقینی بنانے کے لیے استعمال کیا جاتا ہے کہ بائنری ٹری زیادہ سے زیادہ ہیپ ہے۔ اگر ہم ایک نوڈ پر ہیں، n، اور اس کے چائلڈ نوڈس، بائیں اور دائیں بھی خود زیادہ سے زیادہ ہیپس ہیں، تو بہت اچھا، ہمارے پاس زیادہ سے زیادہ ہیپ ہے۔ اگر پورے درخت میں ایسا نہیں ہے تو ہمارے پاس زیادہ سے زیادہ ڈھیر نہیں ہے۔ Max Heapify الگورتھم درخت کو ترتیب دینے کے لیے استعمال کیا جاتا ہے تاکہ یہ maxheap اصولوں پر عمل کرے۔ Max Heapify صرف ایک نوڈ پر کام کرتا ہے۔ اگر ضرورت یہ ہے کہ صف ایک زیادہ سے زیادہ ہیپ اری ہے، تو تمام ذیلی درختوں کو جڑ سے پہلے میکس ہیپ میں تبدیل کرنا ضروری ہے، ایک وقت میں ایک۔ الگورتھم کو ہر نوڈ پر استعمال کیا جانا چاہیے۔ یہ N/2 نوڈس پر کیا جائے گا (پتے زیادہ سے زیادہ ہیپ کی ضروریات پر عمل کریں گے)۔ ہیپ کی وقتی پیچیدگی O(NlogN) ہے، اور اونچائی X پر ایک نوڈ کے لیے، وقت کی پیچیدگی O(X) ہے۔ درج ذیل کوڈ سے پتہ چلتا ہے کہ درخت (ایک صف) کو زیادہ سے زیادہ ہیپیفائی کرنے کا طریقہ۔

public class MaxHeapify

{
   public static Integer[] maxHeapify(Integer[ ] array, Integer i)
   {
       // Create left-child and right-child for the node in question
       Integer leftChild = 2 * i + 1;
       Integer rightChild = 2 * i + 2;

       // Assign maxVal to parent node, i
       Integer maxVal = i;

       // Set maxVal to greater of the two: node or left-child
       if( leftChild < array.length && array[leftChild] > array[maxVal] )
           maxVal = leftChild;

       // Set maxVal to greater of the two: maxVal or right-child
       if( rightChild < array.length && array[rightChild] > array[maxVal] )
           maxVal = rightChild;

       // Check if maxVal is not equal to parent node, then set parent node to
       // maxVal, swap values and then do a maxheapify on maxVal
       // which is now the previous parent node
       if( maxVal != i )
       {
           Integer value = array[i];
           array[i] = array[maxVal];
           array[maxVal] = value;
           array = maxHeapify(array, maxVal);
       }

       return array;
   }


   public static Integer[] maxHeapCreate(Integer array[])
   {
       // Call maxHeapify to arrange array in a max heap
       Integer [] theNewArr = array;
       for( Integer i = array.length/2; i >= 0; i-- )
           theNewArr = maxHeapify(array, i);

       return theNewArr;
   }

   public static void main(String[] args)
   {
       // Create array to be maxheapified, theArray,
       // and array, newArray, to write results into, by calling maxheapCreate
       // newArray will now be a maxheap
       Integer[] theArray = {5, 3, 13, 10, 99, 19, 6, 51, 9};
       Integer[ ] newArray = maxHeapCreate(theArray);

       // Print out contents of newArray
       System.out.println("newArray:");
       for(int i = 0; i < newArray.length; ++i)
       {
           System.out.println(newArray[i]);
       }

       // Print out labelled contents of newArray
       System.out.println(" root : " + newArray[0]);
       for (int i = 0; i <= newArray.length/2 - 1; i++) {
           System.out.print(" parent node : " + newArray[i] + " left child : " +
                            newArray[(2*i)+1] + " right child :" + newArray[(2*i)+2]);
           System.out.println();
       }
  }
}

آؤٹ پٹ دینا: اس کوڈ میں، TheArray بنائی گئی ہے اور نمبروں سے بھری ہوئی ہے۔ ایک دوسری صف، newArray ، بنائی گئی ہے اور اس بار اس میں طریقہ کا نتیجہ ہوگا، maxheapCreate ، max heap array۔ طریقہ maxHeapCreate کو main سے بلایا جاتا ہے ، اور یہاں ایک نئی صف، theNewArr ، بنائی جاتی ہے اور maxHeapify نتائج سے بھر جاتی ہے۔ یہ ان پٹ سرنی کے نصف سائز سے زیادہ لوپ کرکے کیا جاتا ہے۔ لوپ کے ہر پاس کے لیے، طریقہ maxHeapify ، کو کہا جاتا ہے جو کہ صف کے بیچ میں عنصر سے شروع ہوتا ہے اور پہلے کے ساتھ ختم ہوتا ہے۔ maxHeapify کی ہر کال کے لیے ، پیرنٹ نوڈ، i، کے بائیں بچے اور دائیں بچے کو تلاش کیا جاتا ہے اور یہ معلوم کرنے کے لیے جانچ پڑتال کی جاتی ہے کہ تینوں میں سے کون بڑا ہے، اس کی وضاحت maxVal کے طور پر کی جاتی ہے ۔ اگر maxVal پیرنٹ نوڈ کے برابر نہیں ہے تو ایک سویپ کیا جاتا ہے تاکہ پیرنٹ نوڈ اور maxVal کو تبدیل کر دیا جائے اور پھر maxHeapify کو اس بار maxVal پر دوبارہ کال کیا جائے گا اور وہی اقدامات کیے جائیں گے جو پہلے کیے گئے تھے۔ آخر کار زیادہ سے زیادہ ڈھیر بن جائے گا اور اس پر عمل کرنے کے لیے مزید تکرار نہیں ہوگی۔ اپ ڈیٹ کردہ سرنی، array ، کو اب newArray کے طور پر مین پر واپس کر دیا گیا ہے اور پھر ہر ایک لگاتار عنصر کنسول پر پرنٹ کیا جاتا ہے۔ newArray اب زیادہ سے زیادہ ہیپ ہے۔ نوٹ کریں، جیسا کہ پچھلی مثال میں PriorityQueue کا استعمال کرتے ہوئے نمبر لکھے گئے ہیں: جڑ، والدین کے طور پر جڑ کا دائیں بچہ، والدین کے طور پر جڑ کا بائیں بچہ، والدین کے طور پر پہلے دائیں بچے کا دائیں بچہ، پہلے کا بائیں بچہ لیفٹ چائلڈ بطور والدین، دائیں بچے کے پہلے بائیں بچے کا بطور والدین، پہلے دائیں بچے کا بائیں بچہ بطور والدین، وغیرہ۔ ترجیحی قطار استعمال کرتے وقت وہ ان سے قدرے مختلف ترتیب میں ہوتے ہیں کیونکہ موازنہ لگاتار عناصر کے درمیان کیا جاتا ہے ۔ جبکہ maxheapify مثال میں، نوڈ کا مقابلہ صف میں اگلے دو لگاتار عناصر سے کیا جاتا ہے اور سب سے بڑی قدر کے لیے تبدیل کیا جاتا ہے۔ مختصر میں، دو مختلف الگورتھم استعمال کیے جاتے ہیں۔ دونوں ایک زیادہ سے زیادہ ڈھیر بناتے ہیں۔

نتیجہ

تو یہاں ہم نے زیادہ سے زیادہ ہیپ کو دیکھا ہے اور اسے ترجیحی قطار یا میکس ہیپائف الگورتھم کے ساتھ کیسے بنایا جا سکتا ہے۔ reverseOrder() کے ساتھ PriorityQueue استعمال کرنا ایسا کرنے کا ایک صاف طریقہ اور تجویز کردہ طریقہ ہے۔ تاہم، آپ ان مثالوں کا مطالعہ کر سکتے ہیں اور اپنے طریقے خود لکھ سکتے ہیں کیونکہ یہ ایک اچھی کوڈنگ مشق ہوگی جو آپ کو جاوا جونیئر کے انٹرویو میں کامیاب ہونے میں مدد فراہم کرے گی۔