ملازمت کے انٹرویوز سے سوال و جواب: جاوا میں الگورتھم، حصہ 2

یہ الگورتھم کے مختصر جائزہ کا دوسرا حصہ ہے۔ پہلے مضمون کا لنک یہ ہے ۔ اس سے پہلے ہم نے صفوں کو ترتیب دینے کے لیے مختلف الگورتھم کے ساتھ ساتھ نام نہاد لالچی الگورتھم کو دیکھا۔ آج ہم گرافس اور ان سے وابستہ الگورتھم کے بارے میں بات کریں گے۔ گراف پروگرامنگ میں سب سے زیادہ لچکدار اور ورسٹائل ڈھانچے میں سے ایک ہے۔ گراف G کی تعریف عام طور پر سیٹوں کے جوڑے سے کی جاتی ہے، یعنی G = (V، R)، جہاں:

• V چوٹیوں کا ایک مجموعہ ہے۔
• R خطوط کے جوڑوں کو جوڑنے والی لائنوں کا ایک مجموعہ ہے۔

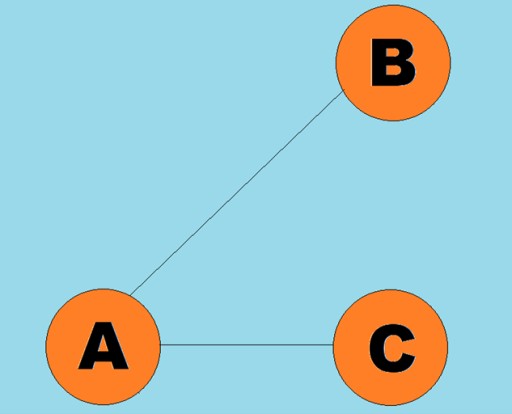غیر مستقیم جڑنے والی لائنوں کو کنارے کہتے ہیں: ڈائریکٹڈ لائنوں کو آرکس کہا جاتا ہے: 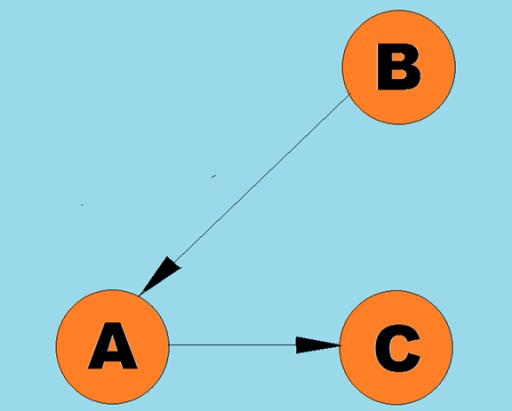عام طور پر، ایک گراف کو ایک خاکہ کے ذریعہ دکھایا جاتا ہے جس میں کچھ عمودی کناروں (آرکس) کے ذریعہ جڑے ہوتے ہیں۔ وہ گراف جن کے کنارے ٹراورسل کی سمت کی نشاندہی کرتے ہیں انہیں ڈائریکٹڈ گراف کہتے ہیں۔ اگر کوئی گراف ایسے کناروں سے جڑا ہوا ہے جو ٹراورسل کی سمت کی نشاندہی نہیں کرتا ہے، تو ہم کہتے ہیں کہ یہ ایک غیر ہدایت شدہ گراف ہے۔ اس کا مطلب یہ ہے کہ حرکت دونوں سمتوں میں ممکن ہے: دونوں سمتوں میں A سے vertex B تک، اور vertex B سے vertex A تک۔ A منسلک گراف ایک ایسا گراف ہے جس میں کم از کم ایک راستہ ہر ایک چوٹی سے کسی دوسرے سرے کی طرف جاتا ہے (جیسا کہ اوپر کی مثال)۔ اگر ایسا نہیں ہے، تو گراف کو منقطع کہا جاتا ہے: 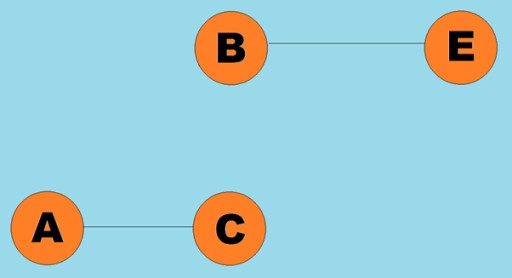کناروں (آرکس) کو وزن بھی تفویض کیا جا سکتا ہے۔ وزن وہ اعداد ہوتے ہیں جو مثال کے طور پر دو چوٹیوں کے درمیان جسمانی فاصلہ (یا دو چوٹیوں کے درمیان رشتہ دار سفر کا وقت) کی نمائندگی کرتے ہیں۔ ان گرافوں کو وزنی گراف کہا جاتا ہے: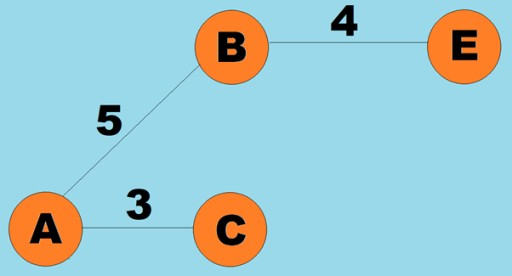

3. پاتھ فائنڈنگ الگورتھم (گہرائی پہلے، چوڑائی پہلے)

گراف کے ساتھ کئے جانے والے بنیادی آپریشنز میں سے ایک دیے گئے چوٹی سے قابل رسائی تمام چوٹیوں کا تعین کرنا ہے۔ تصور کریں کہ آپ اس بات کا تعین کرنے کی کوشش کر رہے ہیں کہ آپ ممکنہ منتقلی سمیت ایک شہر سے دوسرے شہر بس میں کیسے سوار ہو سکتے ہیں۔ کچھ شہروں تک براہ راست پہنچا جا سکتا ہے جبکہ کچھ دوسرے شہروں سے گزر کر ہی پہنچا جا سکتا ہے۔ بہت سی دوسری صورتیں ہیں جہاں آپ کو ان تمام چوٹیوں کو تلاش کرنے کی ضرورت پڑسکتی ہے جن تک آپ کسی دیے ہوئے چوٹی سے پہنچ سکتے ہیں۔ گراف کو عبور کرنے کے دو اہم طریقے ہیں: گہرائی پہلے اور چوڑائی پہلے۔ ہم ان دونوں کو دریافت کریں گے۔ دونوں طریقے تمام منسلک چوٹیوں کو عبور کرتے ہیں۔ ڈیپتھ فرسٹ اور بریڈتھ فرسٹ الگورتھم کو مزید دریافت کرنے کے لیے، ہم درج ذیل گراف کا استعمال کریں گے:

گہرائی سے پہلی تلاش

یہ گراف ٹراورسل کے سب سے عام طریقوں میں سے ایک ہے۔ گہرائی سے پہلی حکمت عملی یہ ہے کہ گراف میں جتنا ممکن ہو گہرائی میں جائیں۔ پھر ایک ڈیڈ اینڈ پر پہنچنے کے بعد، ہم قریب ترین چوٹی پر واپس آتے ہیں جس نے پہلے ملحقہ چوٹیوں کو دیکھا نہیں تھا۔ یہ الگورتھم اسٹیک پر معلومات ذخیرہ کرتا ہے کہ جب ڈیڈ اینڈ تک پہنچ جائے تو کہاں واپس جانا ہے۔ گہرائی سے پہلے تلاش کے اصول:

1. پہلے سے غیر دیکھے ہوئے ملحقہ ورٹیکس پر جائیں، اس کو بطور دورہ شدہ نشان زد کریں، اور اسے اسٹیک پر دھکیل دیں۔
2. اس چوٹی کی طرف بڑھیں۔
3. مرحلہ 1 کو دہرائیں۔
4. اگر مرحلہ 1 ناممکن ہے، تو پچھلے ورٹیکس پر واپس جائیں اور مرحلہ 1 کو انجام دینے کی کوشش کریں۔ اگر یہ ممکن نہیں ہے، تو اس سے پہلے کی چوٹی پر واپس جائیں، اور اسی طرح، جب تک کہ ہمیں کوئی ایسا ورٹیکس نہ مل جائے جہاں سے ہم ٹراورسل جاری رکھ سکیں۔
5. اس وقت تک جاری رکھیں جب تک کہ تمام عمودی اسٹیک پر نہ ہوں۔

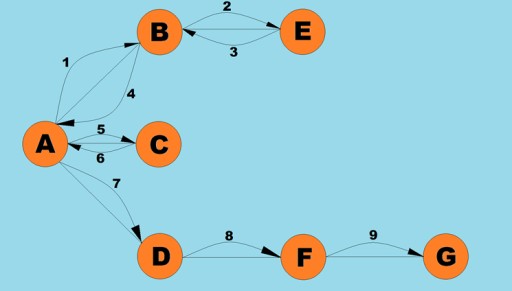آئیے اس پر ایک نظر ڈالتے ہیں کہ اس الگورتھم کا جاوا کوڈ کیسا نظر آتا ہے:

public class Graph {
  private final int MAX_VERTS = 10;
  private Vertex vertexArray[]; // Array of vertices
  private int adjMat[][]; // Adjacency matrix
  private int nVerts; // Current number of vertices
  private Stack stack;

  public Graph() { // Initialize internal fields
     vertexArray = new Vertex[MAX_VERTS];
     adjMat = new int[MAX_VERTS][MAX_VERTS];
     nVerts = 0;
     for (int j = 0; j < MAX_VERTS; j++) {
        for (int k = 0; k < MAX_VERTS; k++) {
           adjMat[j][k] = 0;
        }
     }
     stack = new Stack<>();
  }

  public void addVertex(char lab) {
     vertexArray[nVerts++] = new Vertex(lab);
  }

  public void addEdge(int start, int end) {
     adjMat[start][end] = 1;
     adjMat[end][start] = 1;
  }

  public void displayVertex(int v) {
     System.out.println(vertexArray[v].getLabel());
  }

  public void dfs() { // Depth-first search
     vertexArray[0].setVisited(true); // Take the first vertex
     displayVertex(0);
     stack.push(0);

     while (!stack.empty()) {
        int v = getAdjUnvisitedVertex(stack.peek()); // Return the index of the adjacent vertex: if any, 1; if not, -1
        if (v == -1) { // If there is no unvisited adjacent vertex
           stack.pop(); // The element is removed from the stack
        }
        else {
           vertexArray[v].setVisited(true);
           displayVertex(v);
           stack.push(v); // The element goes on top of the stack
        }
     }

     for (int j = 0; j < nVerts; j++) {  // Reset the flags
        vertexArray[j].visited = false;
     }

  }

  private int getAdjUnvisitedVertex(int v) {
     for (int j = 0; j < nVerts; j++) {
        if (adjMat[v][j] == 1 && vertexArray[j].visited == false) {
           return j; // Returns the first vertex found
        }
     }
     return -1;
  }
}

ایک چوٹی اس طرح نظر آتی ہے:

public class Vertex {
  private char label;  // for example, 'A'
  public boolean visited;

  public Vertex(final char label) {
     this.label = label;
     visited = false;
  }

  public char getLabel() {
     return this.label;
  }

  public boolean isVisited() {
     return this.visited;
  }

  public void setVisited(final boolean visited) {
     this.visited = visited;
  }
}

آئیے اس الگورتھم کو مخصوص چوٹیوں کے ساتھ چلائیں اور دیکھیں کہ آیا یہ صحیح طریقے سے کام کرتا ہے:

public class Solution {
  public static void main(String[] args) {
     Graph graph = new Graph();
     graph.addVertex('A'); //0
     graph.addVertex('B'); //1
     graph.addVertex('C'); //2
     graph.addVertex('D'); //3
     graph.addVertex('E'); //4
     graph.addVertex('F'); //5
     graph.addVertex('G'); //6

     graph.addEdge(0,1);
     graph.addEdge(0,2);
     graph.addEdge(0,3);
     graph.addEdge(1,4);
     graph.addEdge(3,5);
     graph.addEdge(5,6);

     System.out.println("Visits: ");
     graph.dfs();
  }
}

کنسول آؤٹ پٹ: چونکہ ہمارے پاس ملحقہ میٹرکس ہے اور ایک لوپ کے اندر ایک لوپ استعمال کر رہے ہیں، اس لیے وقت کی پیچیدگی O(N²) ہوگی۔

چوڑائی پہلی تلاش

گہرائی سے پہلی تلاش کی طرح، یہ الگورتھم سب سے آسان اور بنیادی گراف ٹراورسل طریقوں میں سے ایک ہے۔ خلاصہ یہ ہے کہ ہمارے پاس کچھ موجودہ ورٹیکس ہے۔ ہم اس کے تمام غیر دیکھے ہوئے ملحقہ عمودی کو ایک قطار میں ڈالتے ہیں اور اگلا عنصر منتخب کرتے ہیں (جو کہ قطار کے سر پر ذخیرہ شدہ چوٹی ہے)، جو موجودہ ورٹیکس بن جاتا ہے… اس الگورتھم کو مراحل میں توڑ کر، ہم درج ذیل مراحل کی شناخت کر سکتے ہیں:

1. موجودہ ورٹیکس سے متصل اگلی پہلے غیر دیکھی ہوئی چوٹی پر جائیں، اسے پہلے سے دیکھے گئے کے بطور نشان زد کریں، اور اسے قطار میں شامل کریں۔
2. اگر مرحلہ نمبر 1 انجام نہیں دیا جا سکتا ہے، تو قطار سے چوٹی کو ہٹا دیں اور اسے موجودہ ورٹیکس بنائیں۔
3. اگر قدم #1 اور #2 کو انجام نہیں دیا جا سکتا ہے، تو ہم عبور کر چکے ہیں — ہر چوٹی کو عبور کیا گیا ہے (اگر ہمارے پاس منسلک گراف ہے)۔

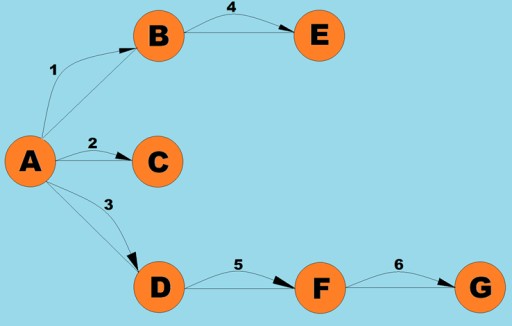یہاں گراف کی کلاس تقریباً اسی سے ملتی جلتی ہے جسے ہم نے گہرائی سے پہلے تلاش کرنے والے الگورتھم کے لیے استعمال کیا تھا، سوائے تلاش کے طریقہ کار کے اور اس حقیقت کے کہ ایک قطار اندرونی اسٹیک کی جگہ لے لیتی ہے:

public class Graph {
  private final int MAX_VERTS = 10;
  private Vertex vertexList[]; // Array of vertices
  private int adjMat[][]; // Adjacency matrix
  private int nVerts; // Current number of vertices
  private Queue queue;

  public Graph() {
     vertexList = new Vertex[MAX_VERTS];
     adjMat = new int[MAX_VERTS][MAX_VERTS];
     nVerts = 0;
     for (int j = 0; j < MAX_VERTS; j++) {
        for (int k = 0; k < MAX_VERTS; k++) {  // Fill the adjacency matrix with zeros
           adjMat[j][k] = 0;
        }
     }
     queue = new PriorityQueue<>();
  }

  public void addVertex(char lab) {
     vertexList[nVerts++] = new Vertex(lab);
  }

  public void addEdge(int start, int end) {
     adjMat[start][end] = 1;
     adjMat[end][start] = 1;
  }

  public void displayVertex(int v) {
     System.out.println(vertexList[v].getLabel());
  }

  public void bfc() { // Depth-first search
     vertexList[0].setVisited(true);
     displayVertex(0);
     queue.add(0);
     int v2;

     while (!queue.isEmpty()) {
        int v = queue.remove();

        while((v2 = getAdjUnvisitedVertex(v))!=-1) {// The loop runs until every adjacent vertex is found and added to the queue
           vertexList[v2].visited = true;
           displayVertex(v2);
           queue.add(v2);
        }
     }

     for (int j = 0; j < nVerts; j++) {  // Reset the flags
        vertexList[j].visited = false;
     }

  }

  private int getAdjUnvisitedVertex(int v) {
     for (int j = 0; j < nVerts; j++) {
        if (adjMat[v][j] == 1 && vertexList[j].visited == false) {
           return j; // Returns the first vertext found
        }
     }
     return -1;
  }
}

ورٹیکس کلاس اس سے ملتی جلتی ہے جسے ہم نے ڈیپتھ فرسٹ سرچ الگورتھم کے ساتھ استعمال کیا۔ آئیے اس الگورتھم کو عمل میں لائیں:

public class Solution {
  public static void main(String[] args) {
     Graph graph = new Graph();
     graph.addVertex('A'); //0
     graph.addVertex('B'); //1
     graph.addVertex('C'); //2
     graph.addVertex('D'); //3
     graph.addVertex('E'); //4
     graph.addVertex('F'); //5
     graph.addVertex('G'); //6

     graph.addEdge(0,1);
     graph.addEdge(0,2);
     graph.addEdge(0,3);
     graph.addEdge(1,4);
     graph.addEdge(3,5);
     graph.addEdge(5,6);

     System.out.println("Visits: ");
     graph.bfc();
  }
}

کنسول آؤٹ پٹ: ایک بار پھر: ہمارے پاس ایک ملحقہ میٹرکس ہے اور لوپ کے اندر اندر ایک لوپ کا استعمال کرتے ہیں، لہذا اوپر والے الگورتھم کی وقت کی پیچیدگی O(N²) ہے۔

4. Dijkstra کا الگورتھم

جیسا کہ پہلے ذکر کیا گیا ہے، گراف کو ڈائریکٹ یا غیر ڈائریکٹ کیا جا سکتا ہے۔ اور آپ کو یاد ہوگا کہ ان کا وزن بھی کیا جا سکتا ہے۔ وزنی، ڈائریکٹڈ گرافس ماڈل تعلقات اکثر حقیقی زندگی میں پائے جاتے ہیں: مثال کے طور پر، شہروں کا نقشہ جہاں شہر عمودی ہیں، اور ان کے درمیان کنارے ایک طرفہ ٹریفک والی سڑکیں ہیں، جو ہدایت شدہ کنارے کی سمت میں بہتی ہیں۔ فرض کریں کہ آپ ایک مال بردار کمپنی ہیں اور آپ کو دو دور دراز شہروں کے درمیان مختصر ترین راستہ تلاش کرنے کی ضرورت ہے۔ آپ یہ کیسے کریں گے؟ دو عمودی خطوط کے درمیان مختصر ترین راستہ تلاش کرنا وزن والے گرافس کا استعمال کرتے ہوئے حل کیے جانے والے سب سے عام مسائل میں سے ایک ہے۔ اس مسئلے کو حل کرنے کے لیے، ہم Dijkstra کا الگورتھم استعمال کرتے ہیں۔ ایک بار جب آپ اسے چلاتے ہیں تو آپ کو دیے گئے ابتدائی چوٹی سے دوسرے ہر ایک تک مختصر ترین راستے معلوم ہوں گے۔ اس الگورتھم کے مراحل کیا ہیں؟ میں اس سوال کا جواب دینے کی کوشش کروں گا۔ Dijkstra کے الگورتھم کے مراحل:

• مرحلہ 1: ملحقہ نوڈ تلاش کریں جس پر نیویگیٹ کرنے کے لیے سب سے کم لاگت ہے (کم ترین کنارے کا وزن)۔ آپ بالکل شروع میں کھڑے ہیں اور سوچ رہے ہیں کہ کہاں جانا ہے: نوڈ A یا نوڈ B تک۔ ان میں سے ہر ایک نوڈس میں جانے کی قیمت کیا ہے؟
• مرحلہ 2: نوڈ В کے ان تمام پڑوسیوں تک سفر کرنے کے لیے فاصلے کا حساب لگائیں جنہیں В سے کنارے سے گزرتے وقت الگورتھم نے ابھی تک نہیں دیکھا ہے۔ اگر نیا فاصلہ پرانے سے کم ہے، تو کنارے B سے گزرنے والا راستہ اس چوٹی کے لیے نیا مختصر ترین راستہ بن جاتا ہے۔
• مرحلہ 3: نشان بی کو بطور ملاحظہ کیا گیا ہے۔
• مرحلہ 4: مرحلہ 1 پر جائیں۔

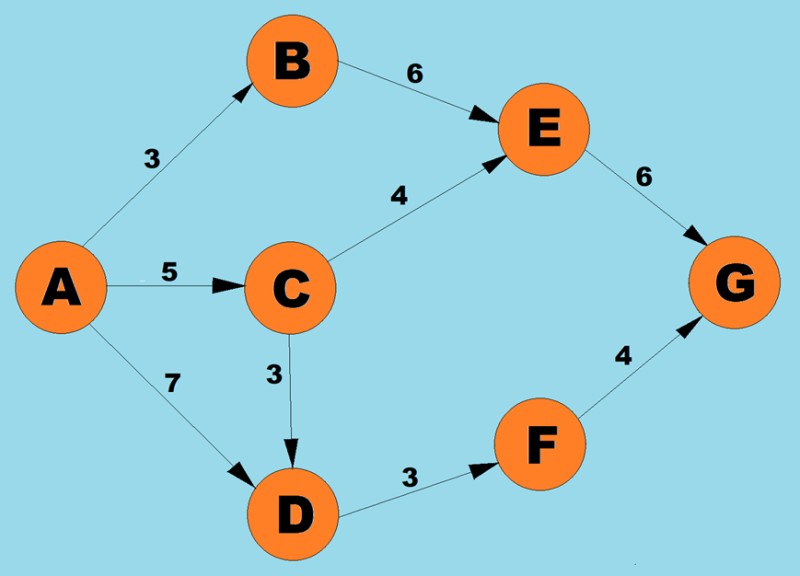ہم ان اقدامات کو ایک لوپ میں دہرائیں گے جب تک کہ تمام عمودیوں کا دورہ نہ کر لیا جائے۔ آئیے درج ذیل وزنی ڈائریکٹڈ گراف پر غور کریں: مندرجہ بالا الگورتھم کا استعمال کرتے ہوئے، ہم A سے G تک کے مختصر ترین راستے کا تعین کریں گے:

1. ورٹیکس A کے لیے تین ممکنہ راستے ہیں: وزن 3 کے ساتھ B تک، وزن 5 کے ساتھ С، اور وزن 7 کے ساتھ D تک۔ الگورتھم کے پہلے مرحلے کے مطابق، ہم سب سے کم قیمت (کنارے کا وزن) کے ساتھ نوڈ کا انتخاب کرتے ہیں۔ اس معاملے میں، بی.

2. چونکہ B کا واحد غیر دیکھا ہوا پڑوسی vertex Е ہے، ہم چیک کرتے ہیں کہ اگر ہم اس چوٹی سے گزریں تو راستہ کیا ہوگا۔ 3(AB) + 6(BE) = 9۔

   اس طرح، ہم ریکارڈ کرتے ہیں کہ A سے E تک موجودہ مختصر ترین راستہ 9 ہے۔

3. چونکہ vertex B کے ساتھ ہمارا کام مکمل ہو گیا ہے، اس لیے ہم اگلے ورٹیکس کو منتخب کرنے کے لیے آگے بڑھتے ہیں جس کے کنارے کا وزن کم سے کم ہے۔

   عمودی A اور B سے، امکانات D (7)، C (5) یا E (6) ہیں۔

   С کے کنارے کا وزن سب سے چھوٹا ہے، لہذا ہم اس چوٹی پر جاتے ہیں۔

4. اگلا، جیسا کہ پہلے، ہم C سے گزرتے وقت ہمسایہ خطوط کا مختصر ترین راستہ تلاش کرتے ہیں:

   • AD = 5 (AC) + 3 (CD) = 8، لیکن چونکہ پچھلا مختصر ترین راستہ (AC = 7) С کے ذریعے اس سے کم ہے، ہم مختصر ترین راستہ (AC = 7) کو کوئی تبدیلی نہیں رکھتے ہیں۔

   • CE = 5(AC) + 4(CE) = 9۔ یہ نیا مختصر ترین راستہ پچھلے راستے کے برابر ہے، اس لیے ہم اسے بھی بغیر تبدیلی کے چھوڑ دیتے ہیں۔

5. قریب ترین قابل رسائی چوٹیوں (E اور D) سے، سب سے چھوٹے کنارے کے وزن کے ساتھ چوٹی کو منتخب کریں، یعنی D (3)۔

6. ہمیں اس کے پڑوسی ایف کا مختصر ترین راستہ ملتا ہے۔

   AF = 7(AD) + 3(DF) = 9

7. قریب ترین قابل رسائی چوٹیوں (E اور F) سے، سب سے چھوٹے کنارے کے وزن کے ساتھ چوٹی کو منتخب کریں، یعنی F (3)۔

8. اپنے پڑوسی جی کے لیے مختصر ترین راستہ تلاش کریں۔

   AG = 7(AD) + 3(DF) + 4(FG) = 14

   تو، ہمیں A سے G تک کا راستہ مل گیا ہے۔

   لیکن اس بات کو یقینی بنانے کے لیے کہ یہ سب سے چھوٹا ہے، ہمیں vertex E پر بھی اپنے اقدامات کرنے چاہییں۔

9. چونکہ vertex G کا کوئی ہمسایہ خط نہیں ہے جس کی طرف سمت کناروں سے اشارہ کیا گیا ہے، ہمارے پاس صرف E vertex باقی ہے، لہذا ہم اسے منتخب کرتے ہیں۔

10. پڑوسی جی کے لیے مختصر ترین راستہ تلاش کریں۔

    AG = 3 (AB) + 6 (BE) + 6 (EG) = 15۔ یہ راستہ پچھلے مختصر ترین راستے (AG (14)) سے لمبا ہے، اس لیے ہم اس راستے کو بغیر کسی تبدیلی کے چھوڑ دیتے ہیں۔

    چونکہ G کی طرف سے کوئی چوٹی نہیں ہے، اس لیے الگورتھم پر قدموں کو اس چوٹی پر چلانا کوئی معنی نہیں رکھتا۔ اس کا مطلب ہے کہ الگورتھم کا کام مکمل ہو گیا ہے۔

جیسا کہ میں نے پہلے کہا، AG کے لیے مختصر ترین راستہ تلاش کرنے کے علاوہ، ہم نے vertex A سے ہر دوسرے vertex (AB, AC, AD, AE, AF) تک مختصر ترین راستے بھی حاصل کیے ہیں۔ ٹھیک ہے، اب یہ جاوا میں کیسے کیا جا سکتا ہے اس پر ایک نظر ڈالنے کا وقت ہے۔ آئیے ورٹیکس کلاس کے ساتھ شروع کریں:

public class Vertex {
   private char label;
   private boolean isInTree;

   public Vertex(char label) {
       this.label = label;
       this.isInTree = false;
   }

   public char getLabel() {
       return label;
   }

   public void setLabel(char label) {
       this.label = label;
   }

   public boolean isInTree() {
       return isInTree;
   }

   public void setInTree(boolean inTree) {
       isInTree = inTree;
   }
}

ورٹیکس کلاس تقریباً چوڑائی کی پہلی تلاش کے لیے استعمال ہونے والی ورٹیکس کلاس سے مماثل ہے۔ مختصر ترین راستوں کو ظاہر کرنے کے لیے، ہمیں ایک نئی کلاس کی ضرورت ہے جس میں وہ ڈیٹا ہوگا جس کی ہمیں ضرورت ہے:

public class Path { // A class that contains the distance and the previous and traversed vertices
   private int distance; // Current distance from the starting vertex
   private List parentVertices; // Current parent vertex

   public Path(int distance) {
       this.distance = distance;
       this.parentVertices = new ArrayList<>();
   }

   public int getDistance() {
       return distance;
   }

   public void setDistance(int distance) {
       this.distance = distance;
   }

   public List getParentVertices() {
       return parentVertices;
   }

   public void setParentVertices(List parentVertices) {
       this.parentVertices = parentVertices;
   }
}

اس کلاس میں، ہم راستے کی کل مسافت اور ان چوٹیوں کو دیکھ سکتے ہیں جو مختصر ترین راستے پر گزرتے وقت گزریں گے۔ اور اب ہم اس کلاس کو دیکھتے ہیں جہاں ہم اصل میں گراف کے ذریعے مختصر ترین راستہ عبور کرتے ہیں۔ تو یہاں ہمارے پاس گراف کلاس ہے:

public class Graph {
   private final int MAX_VERTS = 10;// Maximum number of vertices
   private final int INFINITY = 100000000; // This number represents infinity
   private Vertex vertexList[]; // List of vertices
   private int relationMatrix[][]; // Matrix of edges between vertices
   private int numberOfVertices; // Current number of vertices
   private int numberOfVerticesInTree; // Number of visited vertices in the tree
   private List shortestPaths; // List of shortest paths
   private int currentVertex; // Current vertex
   private int startToCurrent; // Distance to currentVertex

   public Graph() {
       vertexList = new Vertex[MAX_VERTS]; // Adjacency matrix
       relationMatrix = new int[MAX_VERTS][MAX_VERTS];
       numberOfVertices = 0;
       numberOfVerticesInTree = 0;
       for (int i = 0; i < MAX_VERTS; i++) { // Fill the adjacency matrix
           for (int k = 0; k < MAX_VERTS; k++) { // with "infinity"
               relationMatrix[i][k] = INFINITY; // Assign default values
               shortestPaths = new ArrayList<>(); // Assign an empty list
           }
       }
   }

   public void addVertex(char lab) {// Assign new vertices
       vertexList[numberOfVertices++] = new Vertex(lab);
   }

   public void addEdge(int start, int end, int weight) {
       relationMatrix[start][end] = weight; // Set weighted edges between vertices
   }

   public void path() { // Choose the shortest path
       // Set the initial vertex data
       int startTree = 0; // Start from vertex 0
       vertexList[startTree].setInTree(true); // Include the first element in the tree
       numberOfVerticesInTree = 1;

       // Fill out the shortest paths for vertices adjacent to the initial vertex
       for (int i = 0; i < numberOfVertices; i++) {
           int tempDist = relationMatrix[startTree][i];
           Path path = new Path(tempDist);
           path.getParentVertices().add(0);// The starting vertex will always be a parent vertex
           shortestPaths.add(path);
       }
       // Until every vertex is in the tree
       while (numberOfVerticesInTree < numberOfVertices) { // Do this until the number of of vertices in the tree equals the total number of vertices
           int indexMin = getMin();// Get the index of the of the vertex with the smallest distance from the vertices not yet in the tree
           int minDist = shortestPaths.get(indexMin).getDistance(); // Minimum distance to the vertices not yet in the tree

           if (minDist == INFINITY) {
               System.out.println("The graph has an unreachable vertex");
               break; // If only unreachable vertices have not been visited, then we exit the loop
           } else {
               currentVertex = indexMin; // Set currentVert to the index of the current vertex
               startToCurrent = shortestPaths.get(indexMin).getDistance(); // Set the distance to the current vertex
           }

           vertexList[currentVertex].setInTree(true);  // Add the current vertex to the tree
           numberOfVerticesInTree++; // Increase the count of vertices in the tree
           updateShortestPaths(); // Update the list of shortest paths
       }

       displayPaths(); // Display the results on the console
   }

   public void clear() { // Clear the tree
       numberOfVerticesInTree = 0;
       for (int i = 0; i < numberOfVertices; i++) {
           vertexList[i].setInTree(false);
       }
   }

   private int getMin() {
       int minDist = INFINITY; // The distance of the initial shortest path is taken to be infinite
       int indexMin = 0;
       for (int i = 1; i < numberOfVertices; i++) { // For each vertex
           if (!vertexList[i].isInTree() && shortestPaths.get(i).getDistance() < minDist) { // If the vertex is not yet in the tree and the distance to the vertex is less than the current minimum
               minDist = shortestPaths.get(i).getDistance(); // then update the minimum
               indexMin = i; // Update the index of the vertex with the minimum distance
           }
       }
       return indexMin; // Returns the index of the vertex with the smallest distance among those not yet in the tree
   }

   private void updateShortestPaths() {
       int vertexIndex = 1; // The initial vertex is skipped
       while (vertexIndex < numberOfVertices) { // Run over the columns

           if (vertexList[vertexIndex].isInTree()) { // If the column vertex is already in the tree, then we skip it
               vertexIndex++;
               continue;
           }
           // Calculate the distance for one element sPath
           // Get the edge from currentVert to column
           int currentToFringe = relationMatrix[currentVertex][vertexIndex];
           // Add up all the distances
           int startToFringe = startToCurrent + currentToFringe;
           // Determine the distance to the current vertexIndex
           int shortPathDistance = shortestPaths.get(vertexIndex).getDistance();

           // Compare the distance through currentVertex with the current distance in the vertex with index vertexIndex
           if (startToFringe < shortPathDistance) { // If it is smaller, then the vertex at vertexIndex is assigned the new shortest path
               List newParents = new ArrayList<>(shortestPaths.get(currentVertex).getParentVertices()); // Create a copy of the list of vertices of vertex currentVert's parents
               newParents.add(currentVertex); // And add currentVertex to it as the previous vertex
               shortestPaths.get(vertexIndex).setParentVertices(newParents); // Save the new path
               shortestPaths.get(vertexIndex).setDistance(startToFringe); // Save the new distance
           }
           vertexIndex++;
       }
   }

   private void displayPaths() { // A method for displaying the shortest paths on the screen
       for (int i = 0; i < numberOfVertices; i++) {
           System.out.print(vertexList[i].getLabel() + " = ");
           if (shortestPaths.get(i).getDistance() == INFINITY) {
               System.out.println("0");
           } else {
               String result = shortestPaths.get(i).getDistance() + " (";
               List parents = shortestPaths.get(i).getParentVertices();
               for (int j = 0; j < parents.size(); j++) {
                   result += vertexList[parents.get(j)].getLabel() + " -> ";
               }
               System.out.println(result + vertexList[i].getLabel() + ")");
           }
       }
   }
}

تو یہ سب جادو ہے =) اب، آئیے اس الگورتھم پر ایک نظر ڈالتے ہیں:

public class Solution {

   public static void main(String[] args) {
       Graph graph = new Graph();
       graph.addVertex('A');
       graph.addVertex('B');
       graph.addVertex('C');
       graph.addVertex('D');
       graph.addVertex('E');
       graph.addVertex('F');
       graph.addVertex('G');

       graph.addEdge(0, 1, 3);
       graph.addEdge(0, 2, 5);
       graph.addEdge(0, 3, 7);
       graph.addEdge(1, 4, 6);
       graph.addEdge(2, 4, 4);
       graph.addEdge(2, 3, 3);
       graph.addEdge(3, 5, 3);
       graph.addEdge(4, 6, 6);
       graph.addEdge(5, 6, 4);

       System.out.println("The following nodes form the shortest paths from node A:");
       graph.path();
       graph.clear();
   }
}

اور کنسول آؤٹ پٹ یہ ہے: اس الگورتھم کی وقتی پیچیدگی O(N²) کے علاوہ کوئی نہیں ہے، کیونکہ ہمارے پاس نیسٹڈ لوپس ہیں۔ آج میرے پاس بس اتنا ہی ہے۔ آپ کی توجہ کے لئے شکریہ!