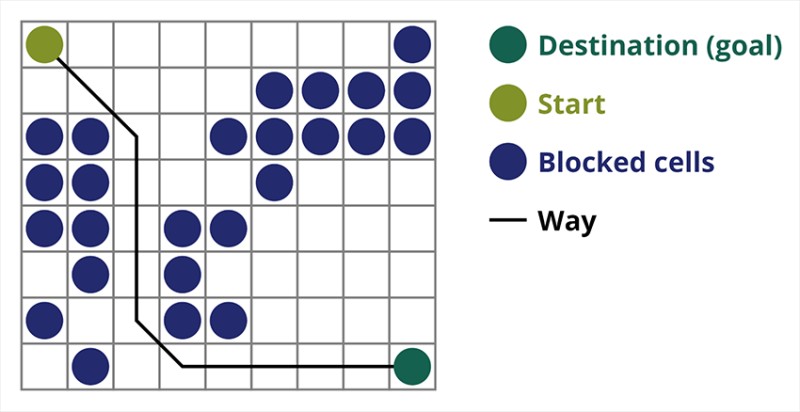
مختلف سرچ الگورتھم مختلف کاموں کے لیے تیار کیے گئے ہیں۔ آج ہم A* سرچ کے بارے میں بات کرنے جا رہے ہیں، جو کہ سب سے زیادہ موثر پاتھ فائنڈنگ الگورتھم میں سے ایک ہے۔ یہ کمپیوٹر گیمز اور سرچنگ گراف بنانے کے لیے بہت موزوں ہے جیسے شہروں کے درمیان راستے وغیرہ۔ آپ نے دیکھا ہو گا، مثال کے طور پر، اسٹریٹجک یا ٹیکٹیکل ویڈیو گیمز میں، کس طرح ایک بٹن دبانے کے بعد، آپ کا کھلاڑی یا گروپ بغیر کسی تاخیر کے فوراً شروع ہو جاتا ہے تاکہ آپ کے بتائے ہوئے مقام تک میدان میں جائیں۔ اس میں قطعی طور پر کوئی تاخیر نہیں ہوتی کیونکہ گیمز موثر الگورتھم استعمال کرتے ہیں جو اس بات کا حساب لگاتے ہیں کہ کھلاڑی کو کسی جگہ پہنچنے کے لیے کس طرح کی ضرورت ہے۔ یا کوئی دشمن جو بلاشبہ کھلاڑی کو ڈھونڈتا ہے اور دور سے صحیح سمت میں چلنا شروع کر دیتا ہے۔ عام طور پر، A* الگورتھم ایسی کارروائیوں کے لیے استعمال ہوتا ہے۔
A* الگورتھم کیا ہے؟
پاتھ فائنڈنگ الگورتھم A* بہترین پہلی تلاش کے الگورتھم کی ایک مثال ہے۔ A* الگورتھم کا مقصد ایک نقطہ سے دوسرے مقام تک راستہ تلاش کرنا ہے۔ یہ گراف الگورتھم کی تلاش کے لیے کلاسیکی میں سے ایک ہے۔ آئیے ایک مثال کا استعمال کرتے ہوئے معلوم کریں کہ یہ کیسے کام کرتا ہے۔ اوپر سے نیچے کے نظارے کے ساتھ 2D گیم کا تصور کریں۔ آئیے اپنے کھیل کے علاقے کو مربع لالچ میں تقسیم کرتے ہیں، مثال کے طور پر 8*8 خلیات جیسے کہ بساط۔ ہمارے خلیے دو اقسام میں سے ایک ہو سکتے ہیں، قابل گزر یا ناقابل گزر (رکاوٹ)۔ ہر وقت ایک کھلاڑی یا دشمن جو کھلاڑی کے قریب آتا ہے ایک سیل منتقل کرتا ہے۔ گیمز میں، گزرنے کے قابل سیلز مختلف نوعیت کے ہو سکتے ہیں، مثال کے طور پر، ایک چپٹی سڑک، گھاس یا ریت، جو ان کے ساتھ چلنے میں دشواری کا تعین کرتی ہے، لیکن سادگی کے لیے ہم یہ فرض کریں گے کہ تمام قابل گزر سیل ایک ہی طریقے سے گزرے ہیں۔ نیچے دی گئی تصویر میں نیلے خلیے رکاوٹیں ہیں۔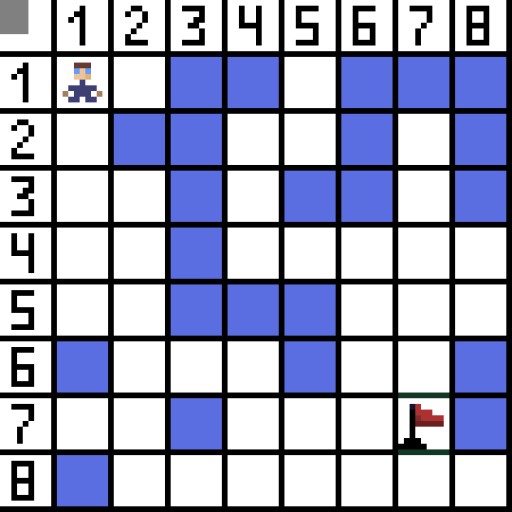
آئیے ایک سیل (یا نوڈ) کو اسٹارٹ سیل کے طور پر تفویض کریں (کریکٹر اس میں ہے)، اور دوسرے سیل کو ٹارگٹ یا گول سیل (جھنڈے والا) کے طور پر، اور اس کیس کے لیے A* الگورتھم کیسے کام کرتا ہے اس کی وضاحت کریں۔ کردار سیل (1,1) میں ہے اور ہدف سیل (7,7) میں ہے۔ ہر خلیے کے افقی، عمودی اور ترچھے پڑوسی ہوتے ہیں۔ یہ کھیل پر منحصر ہے، اگر ہم اخترن نوڈس کا حساب لگاتے ہیں یا نہیں۔ مثال کے طور پر بہت سے ٹاپ ڈاون ویو گیمز جیسے کہ Bomberman یا Pacman میں کردار صرف افقی یا عمودی طور پر حرکت کر سکتے ہیں۔ اس صورت میں ہر نوڈ، کناروں کو چھونے کے علاوہ، صرف 4 پڑوسی ہیں۔ اگر ہم ایک ایسے کھیل کے بارے میں بات کر رہے ہیں جہاں کردار ترچھی حرکت کر سکتے ہیں، تو ہر نوڈ میں 8 پڑوسی ہو سکتے ہیں۔ الگورتھم کے پہلے مرحلے پر، سیل جہاں کریکٹر واقع ہے اس کے دو پڑوسی ہوتے ہیں۔ زیادہ واضح طور پر، تین، لیکن ان میں سے ایک رکاوٹ ہے. 
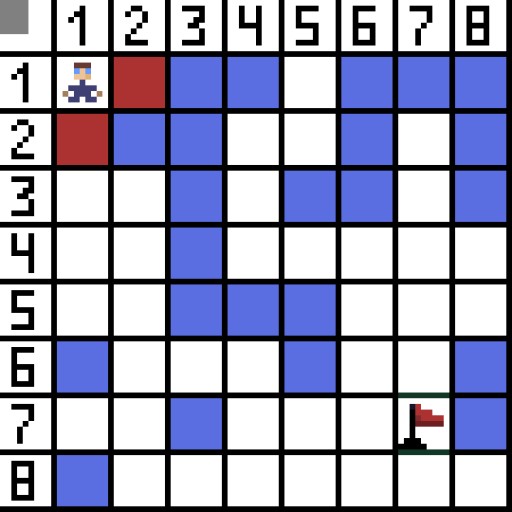یہ واضح ہے کہ ترچھا راستہ لمبا ہے۔ اگر ہم اپنے خلیے کا رخ مشروط طور پر ایک کے برابر مقرر کرتے ہیں، تو اس خلیے کے اخترن کی لمبائی دو کے مربع جڑ کے برابر ہے۔ پائتھاگورین تھیوریم یہی کہتا ہے۔ سیل A سے سیل B تک جانے کے لیے، آپ کو پہلے پڑوسی سیلز میں سے ایک کو منتخب کرنا ہوگا، اور پھر اگلا، وغیرہ۔ اس کے علاوہ، راستے میں، یہ سمجھیں کہ آیا ابتدائی سیل سے ہدف تک پہنچنا ممکن ہے۔ ہر قدم پر A* الگورتھم فنکشن F کی قدر کے مطابق پڑوسی سیلوں میں سے ایک کو منتخب کرتا ہے۔ یہ فنکشن پیمائش کرتا ہے کہ ہمارے مختصر ترین راستے میں امیدوار سیل کو شامل کرنا کتنا اچھا ہے۔ یہ لاگت کا فنکشن ہے، اور یہ موو فنکشن G اور ہیورسٹک فنکشن کا مجموعہ ہے۔
-
جی لاگت - ایک ابتدائی نوڈ سے ایک فاصلہ ہے۔
-
H لاگت (Heuristic) اختتام (مقصد) نوڈ سے ایک فاصلہ ہے۔ یہ فنکشن مختلف ہو سکتا ہے، ایک ڈویلپر فیصلہ کرتا ہے کہ کیا بہتر ہے۔ شاید A* میں H کا انتخاب سب سے اہم ہے، اور یہی وہ نکتہ ہے جو الگورتھم کے کسی خاص نفاذ کو کم و بیش موثر بناتا ہے۔ نظریاتی طور پر آپ کسی بھی فنکشن کو استعمال کرسکتے ہیں جو آپ چاہتے ہیں۔
ہمارے معاملے میں، ہم ٹارگٹ سیل کی پوزیشن کو جانتے ہیں اور مثال کے طور پر، ہدف اور موجودہ سیل کے درمیان ہندسی یوکلیڈین فاصلے کا حساب لگا سکتے ہیں۔ فاصلہ جتنا کم ہوگا ہم مقصد کے اتنے ہی قریب ہوں گے۔
-
F لاگت = G + H۔ لہٰذا الگورتھم تمام پڑوسی نوڈس F کے اخراجات کا حساب لگاتا ہے اور سب سے کم F قیمتوں میں سے ایک کا انتخاب کرتا ہے جو پہلے دیکھنے کے لیے ہوتا ہے۔ جب ہم ایک کا انتخاب کرتے ہیں تو ہم اسے بند کے طور پر نشان زد کرتے ہیں اور اس نوڈ پڑوسیوں کے لیے قدروں کا حساب لگاتے ہیں۔
Heuristic function ہم H کا حساب کیسے لگا سکتے ہیں؟
یہ ایک heuristic تقریب ہے. نام کا خود مطلب یہ ہے کہ اس کا تعین تجربے سے ہوتا ہے، اور مختلف ہو سکتا ہے۔ یہاں ہم اسے پوائنٹس (x1, y1) اور (x2, y2) کے درمیان نام نہاد Euclidean فاصلے کے برابر لیں گے: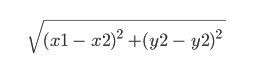
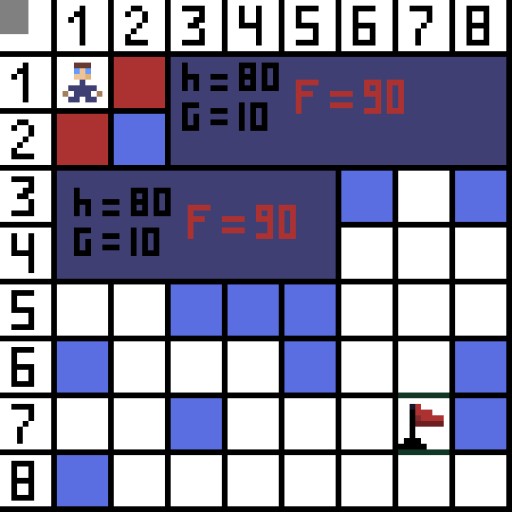تصویر میں، پہلے مرحلے کے لیے، دو اختیارات ہیں، اور وہ لاگت میں ایک جیسے ہیں، لیکن اگلے مرحلے پر، کردار کسی ایک آپشن میں ختم ہو جاتا ہے۔ اس لیے ہم دوسری طرف جا رہے ہیں۔ اگلی تکرار میں، ہمارے پاس پہلے سے ہی 4 اختیارات ہیں۔ 
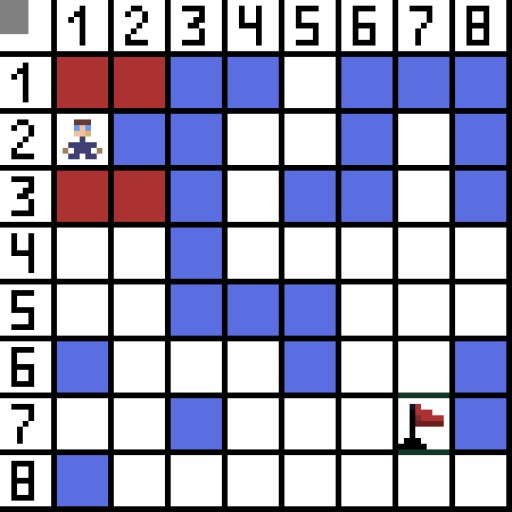ان میں سے دو موزوں نہیں ہیں، کیونکہ وہ پیچھے کی طرف لے جاتے ہیں، اور دوسرے آپشن بھی اتنے ہی اچھے ہیں، لیکن الگورتھم نے فیصلہ کیا کہ سیل (3,2) تک ترچھی جانا ہی بہتر ہے۔ مزید، ہر قدم پر، فنکشن F کا حساب اس وقت تک دہرایا جاتا ہے جب تک کہ کریکٹر ٹارگٹ سیل تک نہ پہنچ جائے۔ اگر، یقینا، اس طرح کا ایک حوالہ موجود ہے. 
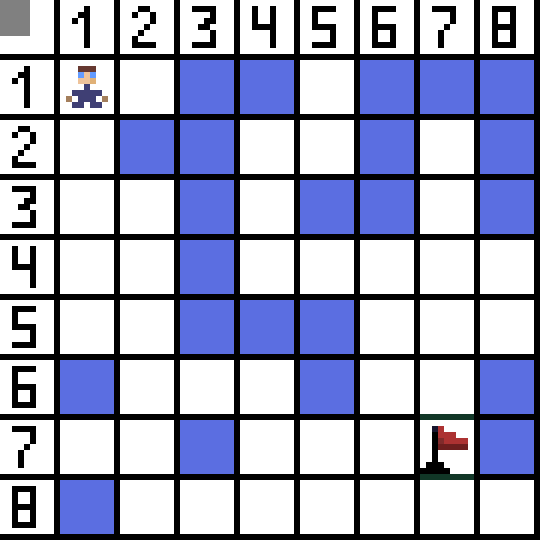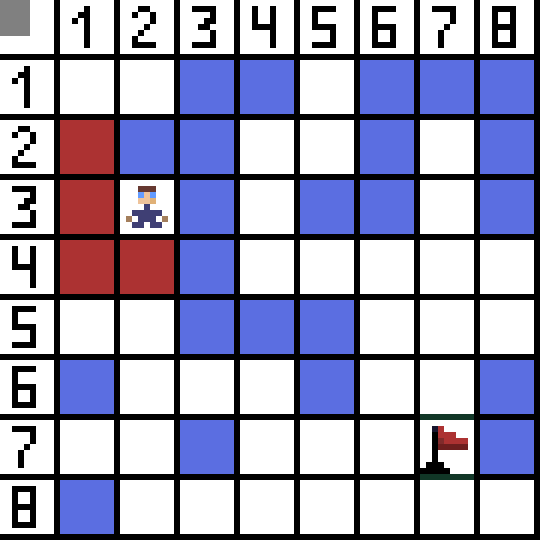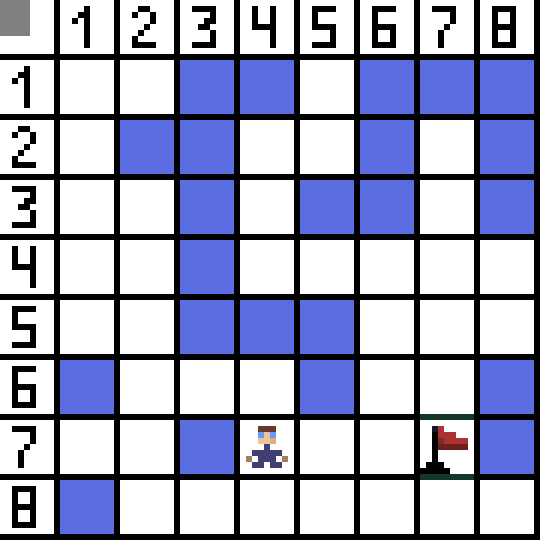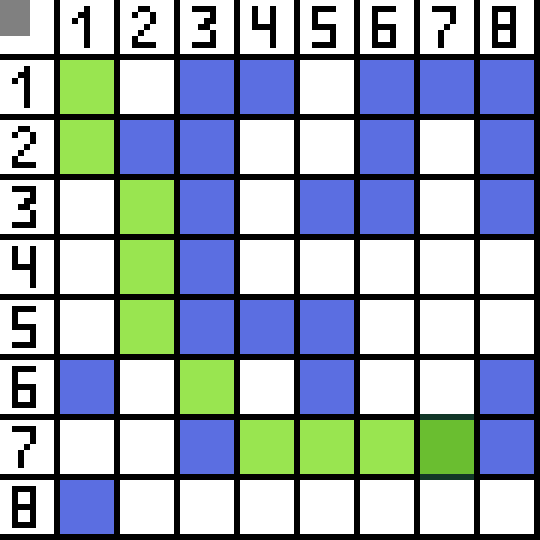GIF-تصویر پر سبز راستہ پرچم کی طرف کردار کے بہترین راستے کی نشاندہی کرتا ہے۔
A* الگورتھم مرحلہ وار
جاوا میں الگورتھم کو لاگو کرنے کے لیے، آپ کو درج ذیل اقدامات کرنے کی ضرورت ہے 1۔ پہلے آپ کو دو فہرستیں بنانے کی ضرورت ہے، کھلے نوڈس اور بند نوڈس کے لیے۔ 2. دونوں فہرستوں کو شروع کریں۔ بند فہرست میں، شروع نوڈ کھلی فہرست کی طرف اشارہ کرتا ہے۔ 3. جبکہ کھلی فہرست میں عناصر موجود ہیں: 3a۔ سب سے چھوٹی F 3b کے ساتھ نوڈ منٹ تلاش کریں۔ کھلی فہرست 3c سے منٹ کو ہٹا دیں۔ پڑوسی منٹ کا تعین کریں (8 تک، اگر اخترن کو مدنظر رکھا جائے) 3d۔ ہر پڑوسی کو چیک کرنا: a) اگر پڑوسی ٹارگٹ سیل ہے تو تلاش کرنا بند کر دیں ب) اگر نہیں تو اس کے لیے G، H کا حساب لگائیں۔ G = min.G + پڑوسی اور min F = G + H کے درمیان فاصلہ c) اگر پڑوسی جیسی پوزیشن والا نوڈ کھلی فہرست میں ہے اور اس کا F پڑوسی سے کم ہے تو اس پڑوسی کو چھوڑ دیں d) اگر بند فہرست میں پڑوسی جیسی پوزیشن والا نوڈ ہے، اور اس کا ایف پڑوسی سے کم ہے، اس پڑوسی کو چھوڑ دیں۔ بصورت دیگر، نوڈ کو اندرونی لوپ 3e کے اختتام کی کھلی فہرست میں شامل کریں۔ بند فہرست میں min شامل کرنا بیرونی لوپ کا اختتام تو، ہر تکرار پر ہم اگلا کرنے جا رہے ہیں:- ہماری کھلی فہرست سے سب سے کم تخمینہ شدہ کل سکور کے ساتھ سیل کو منتخب کریں۔
- اس سیل کو کھلی فہرست سے ہٹا دیں۔
- ان تمام سیلز کو شامل کریں جن تک ہم اس سے کھلی فہرست میں پہنچ سکتے ہیں۔
- جب ہم ایسا کرتے ہیں، تو ہم اس نوڈ سے ہر نئے اسکور کو بھی پروسیس کرتے ہیں تاکہ یہ دیکھیں کہ آیا یہ ہمارے اب تک کی چیزوں میں بہتری ہے، اور اگر یہ ہے، تو ہم اس سیل کے بارے میں جو کچھ جانتے ہیں اسے اپ ڈیٹ کرتے ہیں۔
A* سیڈوکوڈ
یہاں A* پاتھ فائنڈنگ کا مختصر سیوڈوکوڈ ہے:Input: a grid with locked and empty cells, with start and goal cell.
Output: least cost path from start to goal cell.
Initialisation
openList = {startCell} //list of traversed cells
closedList = {} //list of already traversed cells
g.startCell = 0 //cost from source cell to a cell
h.startCell = h(startCell, goal) //heuristic
f.startCell = g.startCell + h.StartCell
while openList is not empty
do
//let the currentCell equal the cell with the least f value
currentCell = Cell on top of openList, with least f
if currentCell == end return
remove currentCell from openList
add currentCell to closedList
foreach n in child.currentCell
if n in closedList
continue
cost = g.currentCell + distance(currentCell,n)
if (n in openList and cost < g.n)
remove n from closedList
g.n = cost
h.n = h(n, goal)
f.n = g.n + h.nجاوا میں سیڈوکوڈ سے A* نفاذ تک
A* جاوا ادراک میں پاتھ فائنڈنگ میں الگورتھم کی خدمت کے لیے کچھ طریقے ہونے چاہئیں:- سیل، ضروری پیرامیٹرز رکھنے کے لیے ایک ڈھانچہ
- کھلی اور بند فہرستیں۔
- ہورسٹک فنکشن کا حساب لگانے کا طریقہ
- منبع سے منزل تک راستے کو ٹریس کرنے کا طریقہ
- یہ چیک کرنے کے طریقے کہ آیا دیا ہوا سیل بلاک ہے، اگر یہ پہلے ہی پہنچ چکا ہے، اگر یہ درست ہے تو وغیرہ
package Asterist;
import java.util.PriorityQueue;
import java.util.Stack;
public class AAsterisk {
//Java Program to implement A* Search Algorithm
//Here we're creating a shortcut for (int, int) pair
public static class Pair {
int first;
int second;
public Pair(int first, int second){
this.first = first;
this.second = second;
}
@Override
public boolean equals(Object obj) {
return obj instanceof Pair && this.first == ((Pair)obj).first && this.second == ((Pair)obj).second;
}
}
// Creating a shortcut for tuple<int, int, int> type
public static class Details {
double value;
int i;
int j;
public Details(double value, int i, int j) {
this.value = value;
this.i = i;
this.j = j;
}
}
// a Cell (node) structure
public static class Cell {
public Pair parent;
// f = g + h, where h is heuristic
public double f, g, h;
Cell()
{
parent = new Pair(-1, -1);
f = -1;
g = -1;
h = -1;
}
public Cell(Pair parent, double f, double g, double h) {
this.parent = parent;
this.f = f;
this.g = g;
this.h = h;
}
}
// method to check if our cell (row, col) is valid
boolean isValid(int[][] grid, int rows, int cols,
Pair point)
{
if (rows > 0 && cols > 0)
return (point.first >= 0) && (point.first < rows)
&& (point.second >= 0)
&& (point.second < cols);
return false;
}
//is the cell blocked?
boolean isUnBlocked(int[][] grid, int rows, int cols,
Pair point)
{
return isValid(grid, rows, cols, point)
&& grid[point.first][point.second] == 1;
}
//Method to check if destination cell has been already reached
boolean isDestination(Pair position, Pair dest)
{
return position == dest || position.equals(dest);
}
// Method to calculate heuristic function
double calculateHValue(Pair src, Pair dest)
{
return Math.sqrt(Math.pow((src.first - dest.first), 2.0) + Math.pow((src.second - dest.second), 2.0));
}
// Method for tracking the path from source to destination
void tracePath(
Cell[][] cellDetails,
int cols,
int rows,
Pair dest)
{ //A* Search algorithm path
System.out.println("The Path: ");
Stack<Pair> path = new Stack<>();
int row = dest.first;
int col = dest.second;
Pair nextNode = cellDetails[row][col].parent;
do {
path.push(new Pair(row, col));
nextNode = cellDetails[row][col].parent;
row = nextNode.first;
col = nextNode.second;
} while (cellDetails[row][col].parent != nextNode); // until src
while (!path.empty()) {
Pair p = path.peek();
path.pop();
System.out.println("-> (" + p.first + "," + p.second + ") ");
}
}
// A main method, A* Search algorithm to find the shortest path
void aStarSearch(int[][] grid,
int rows,
int cols,
Pair src,
Pair dest)
{
if (!isValid(grid, rows, cols, src)) {
System.out.println("Source is invalid...");
return;
}
if (!isValid(grid, rows, cols, dest)) {
System.out.println("Destination is invalid...");
return;
}
if (!isUnBlocked(grid, rows, cols, src)
|| !isUnBlocked(grid, rows, cols, dest)) {
System.out.println("Source or destination is blocked...");
return;
}
if (isDestination(src, dest)) {
System.out.println("We're already (t)here...");
return;
}
boolean[][] closedList = new boolean[rows][cols];//our closed list
Cell[][] cellDetails = new Cell[rows][cols];
int i, j;
// Initialising of the starting cell
i = src.first;
j = src.second;
cellDetails[i][j] = new Cell();
cellDetails[i][j].f = 0.0;
cellDetails[i][j].g = 0.0;
cellDetails[i][j].h = 0.0;
cellDetails[i][j].parent = new Pair( i, j );
// Creating an open list
PriorityQueue<Details> openList = new PriorityQueue<>((o1, o2) -> (int) Math.round(o1.value - o2.value));
// Put the starting cell on the open list, set f.startCell = 0
openList.add(new Details(0.0, i, j));
while (!openList.isEmpty()) {
Details p = openList.peek();
// Add to the closed list
i = p.i; // second element of tuple
j = p.j; // third element of tuple
// Remove from the open list
openList.poll();
closedList[i][j] = true;
// Generating all the 8 neighbors of the cell
for (int addX = -1; addX <= 1; addX++) {
for (int addY = -1; addY <= 1; addY++) {
Pair neighbour = new Pair(i + addX, j + addY);
if (isValid(grid, rows, cols, neighbour)) {
if(cellDetails[neighbour.first] == null){ cellDetails[neighbour.first] = new Cell[cols]; }
if (cellDetails[neighbour.first][neighbour.second] == null) {
cellDetails[neighbour.first][neighbour.second] = new Cell();
}
if (isDestination(neighbour, dest)) {
cellDetails[neighbour.first][neighbour.second].parent = new Pair ( i, j );
System.out.println("The destination cell is found");
tracePath(cellDetails, rows, cols, dest);
return;
}
else if (!closedList[neighbour.first][neighbour.second]
&& isUnBlocked(grid, rows, cols, neighbour)) {
double gNew, hNew, fNew;
gNew = cellDetails[i][j].g + 1.0;
hNew = calculateHValue(neighbour, dest);
fNew = gNew + hNew;
if (cellDetails[neighbour.first][neighbour.second].f == -1
|| cellDetails[neighbour.first][neighbour.second].f > fNew) {
openList.add(new Details(fNew, neighbour.first, neighbour.second));
// Update the details of this
// cell
cellDetails[neighbour.first][neighbour.second].g = gNew;
//heuristic function cellDetails[neighbour.first][neighbour.second].h = hNew;
cellDetails[neighbour.first][neighbour.second].f = fNew;
cellDetails[neighbour.first][neighbour.second].parent = new Pair( i, j );
}
}
}
}
}
}
System.out.println("Failed to find the Destination Cell");
}
// test
public static void main(String[] args) {
//0: The cell is blocked
// 1: The cell is not blocked
int[][] grid = {
{ 1, 1, 0, 0, 1, 0, 0, 0 },
{ 1, 0, 0, 1, 1, 0, 1, 0 },
{ 1, 1, 0, 1, 0, 0, 1, 0 },
{ 1, 1, 0, 1, 1, 1, 1, 1 },
{ 1, 1, 0, 0, 0, 1, 1, 1 },
{ 0, 1, 1, 1, 0, 1, 1, 0 },
{ 1, 1, 0, 1, 1, 1, 1, 0 },
{ 0, 1, 1, 1, 1, 1, 1, 1 }
};
// Start is the left-most upper-most corner
Pair src = new Pair(0,0);
//(8, 0);
// Destination is the right-most bottom-most corner
Pair dest = new Pair(6, 6);
AAsterisk app = new AAsterisk();
app.aStarSearch(grid, grid.length , grid[0].length, src, dest);
}
}
راستہ: -> (0,0) -> (1,0) -> (2,1) -> (3,1) -> (4,1) -> (5,2) -> (5، 3) -> (6,4) -> (6,5) -> (6,6)
یہ دیکھا جا سکتا ہے کہ یہ کئی مختصر ترین راستوں میں سے ایک ہے جو ان دو پوائنٹس کے درمیان بنائے جا سکتے ہیں۔ یاد رکھیں کہ تصویر میں اور پروگرام کے آؤٹ پٹ میں ہماری مثال میں چھٹا مرحلہ مختلف ہے، حالانکہ راستے اتنے ہی موثر نکلے ہیں۔ پروگرام بہت سے مؤثر اختیارات میں سے ایک کا انتخاب کرتا ہے۔
GO TO FULL VERSION