জাভাতে ম্যাক্স হিপ

বাইনারি গাছ

জাভাতে, বিভিন্ন ধরণের ডেটা স্ট্রাকচার রয়েছে। স্তূপটি একটি গাছের কাঠামোর উপর ভিত্তি করে যাকে বলা হয় বাইনারি ট্রি । একটি বাইনারি গাছে নোড থাকে, যার প্রতিটিতে সর্বোচ্চ 2টি চাইল্ড নোড থাকতে পারে: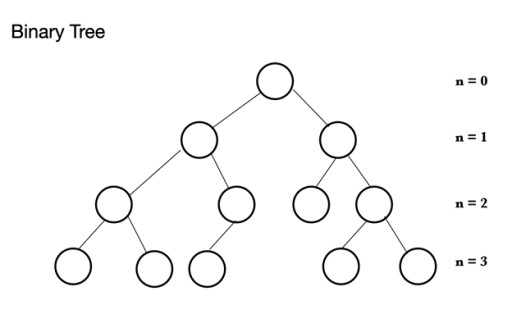 একটি বাইনারি ট্রিতে একটি প্যারেন্ট নোড থাকে যার মধ্যে 0 থেকে 2টি নোড থাকতে পারে। এটিতে একটি বাম-চাইল্ড নোড এবং/অথবা একটি রাইট-চাইল্ড নোড থাকতে পারে, বা কোনও নোড নেই। একটি সম্পূর্ণ বাইনারি গাছে, শেষ স্তর ব্যতীত সমস্ত নোড পূর্ণ হয় যা পূর্ণ হতে পারে, তবে পূর্ণ হওয়ার প্রয়োজন নেই। শেষ স্তর, nম স্তরে 1 থেকে 2n নোড থাকতে পারে, যেখানে প্রথমটি n = 0 এ থাকে এবং এটি মূল।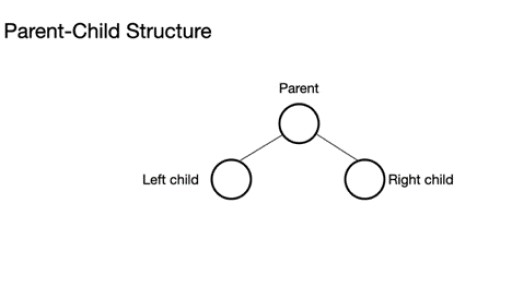

সর্বোচ্চ স্তূপ

ম্যাক্স হিপ (বা ম্যাক্সহিপ) একটি সম্পূর্ণ বাইনারি ট্রি । এটি সম্পর্কে গুরুত্বপূর্ণ বিষয় হল যে প্যারেন্ট নোডের মান অবশ্যই বাম এবং ডান-চাইল্ড নোডের চেয়ে বেশি বা সমান হতে হবে। এটি মেনে না চললে, আপনার কাছে সর্বোচ্চ হিপ নেই। অপরদিকে, মিন হিপ হল রুটের বিপরীতে ছোট মান হিসাবে ক্রমাগত নোডের মান বৃদ্ধির সাথে; প্রতিটি চাইল্ড নোডের মান তার পিতামাতার চেয়ে বেশি বা সমান। এটিও একটি সম্পূর্ণ বাইনারি গাছ। সর্বাধিক হিপের একটি উদাহরণ হল: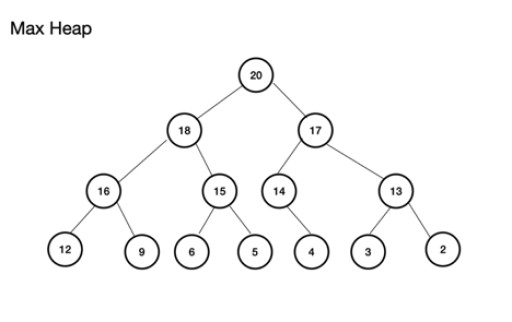 সর্বাধিক হিপ একটি অ্যারে থেকে তৈরি করা যেতে পারে। এই অ্যারে একটি গাছ পদ বিবেচনা করা হবে. একটি গাদা জন্য, যদি রুট, (বৃক্ষের উপরের প্যারেন্ট নোড) অবস্থানে (সূচী) n সংরক্ষণ করা হয়, এটি অ্যারে, theArray-এর জন্য অ্যারে [n] হিসাবে সংজ্ঞায়িত করা হয়।. বাম- এবং ডান-চাইল্ড নোডগুলি যথাক্রমে অ্যারে [2n+1] এবং অ্যারে [2n+2]- এ রয়েছে। সর্বাধিক হিপের জন্য, রুটটি অ্যারেতে রয়েছে [0] । n স্তরের জন্য, রুট n = 0: theArr[n] হল প্যারেন্ট নোড theArr[(2*n)+1] হল বাম চাইল্ড নোড TheArr[(2*n)+2] হল ডান চাইল্ড নোড

অগ্রাধিকার সারি ক্লাস

PriorityQueue ক্লাস ব্যবহার করে জাভাতে হিপস প্রয়োগ করা যেতে পারে । একটি সংগ্রহে সবচেয়ে বা কম গুরুত্বপূর্ণ আইটেম খুঁজে পেতে PriorityQueue ব্যবহার করা হয়৷ PriorityQueue ক্লাসটি java.util.package এ পাওয়া যাবে ৷ অগ্রাধিকার সারিগুলি তুলনীয় বস্তুগুলিকে তৈরি করতে হবে যাতে সেগুলিকে সারিতে একটি নির্দিষ্ট ক্রমে স্থাপন করা হয়। PriorityQueue এর একটি তুলনাকারী থাকতে পারে যাতে বস্তুর মধ্যে তুলনা করা যায় এবং এই তুলনা অনুসারে সারি তৈরি হয়। একটি উদাহরণ হল:

import java.util.Comparator;
import java.util.PriorityQueue;

public class Main
{
    public static void main(String[] args) {
        // Create PriorityQueue with comparator for ascending order of array length
        PriorityQueue intQueue = new PriorityQueue((a,b) -> a - b);
        Integer [] array1 = {1, 2, 4, 6, 8, 9};
        Integer [] array2 = {3, 6, 9};
        Integer [] array3 = {2, 4, 8, 16, 32, 64, 128};
        Integer [] array4 = {5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55};
        Integer [] array5 = {4};

        //Add the array lengths to intQueue
        intQueue.add(array1.length);
        intQueue.add(array2.length);
        intQueue.add(array3.length);
        intQueue.add(array4.length);
        intQueue.add(array5.length);
        //Write out contents of intQueue as stored
        while (intQueue.size() != 0) {
            System.out.println(intQueue.remove());
        }
    }
}

আউটপুট প্রদান: এই উদাহরণে, intQueue- এর ডিফল্ট আকার হল 11, তাই বলা হয়নি (সাধারণত তুলনাকারীর আগে প্রথম আর্গুমেন্ট) এবং তুলনাকারীকে এইভাবে দেওয়া হয়েছে: এটি intQueue- এ থাকা আইটেমগুলির মধ্যে একটি তুলনা করবে এবং এটিকে আরোহী ক্রমের অ্যারে দৈর্ঘ্যে বাছাই করবে।

সর্বাধিক হিপ তৈরি করতে অগ্রাধিকার সারির বাস্তবায়ন

PriorityQueue ক্লাস ডিফল্ট মিন হিপে তুলনাকারী ছাড়া । মিন হিপ হল ম্যাক্স হিপের বিপরীত এবং তাই রুট হল সবচেয়ে ছোট মান এবং ক্রমাগত চাইল্ড নোডগুলি রুট এবং পরবর্তী প্যারেন্টাল নোডের থেকে বড় বা সমান। এই কারণে, সর্বাধিক হিপের জন্য, তুলনাকারী হিসাবে জাভার কালেকশন ফ্রেমওয়ার্ক থেকে reverseOrder() ব্যবহার করা প্রয়োজন । এটি নিশ্চিত করবে যে আমরা একটি সর্বাধিক হিপ পেতে পারি এবং একটি মিনিটের গাদা নয়। এই ক্লাসে দরকারী পদ্ধতি রয়েছে যেমন add() , contains() , remove() , poll() , এবং peek() । উপাদানগুলি সারিতে যোগ করা হয় এবং যেকোনো ক্রমে হতে পারে। নতুন PriorityQueue কিউ সেই উপাদানগুলিকে বিপরীত ক্রমে সর্বাধিক হিপ হিসাবে সংরক্ষণ করবে। সারিটি লেখা হয়ে গেলে, ক্রমটি হবে: রুট বাম-শিশু রুট সহ পিতামাতা হিসাবে (বাম-শিশু_1) পিতামাতা হিসাবে রুট সহ ডান-সন্তান (ডান-শিশু_1) বাম-শিশু বাম-শিশু_1 পিতামাতা হিসাবে (বাম-শিশু_2) ) ডান-সন্তানের সাথে বাম-শিশু_1 পিতামাতা হিসাবে (ডান-সন্তান_2) বাম-সন্তানের সাথে ডান-শিশু_1 পিতামাতা হিসাবে (বাম-সন্তান_3) ডান-সন্তানের সাথে ডান-সন্তান_1 অভিভাবক হিসাবে (ডান-সন্তান_3) বাম-সন্তানের সাথে বাম-সন্তান_2 পিতামাতা হিসাবে (বাম-সন্তান_4) ডান-সন্তানের সাথে বাম-শিশু_2 অভিভাবক হিসাবে (ডান-শিশু_4), ​​ইত্যাদি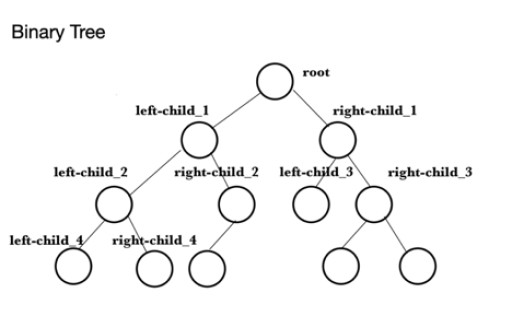নিচের কোডটি জাভাতে কিভাবে একটি max heap (maxheap) তৈরি করা হয় তার একটি উদাহরণ। প্রথম জিনিসটি হল মান দিয়ে একটি অ্যারে পূরণ করা যার জন্য সর্বাধিক হিপ তৈরি করা হবে। একে বলা হয় অ্যারে । এরপরে, একটি PriorityQueue , theQueue , তৈরি করা হয় এবং তারপর অ্যারে থেকে উপাদানগুলি এতে যোগ করা হয়। এটি সারির শেষে 10 যোগ করার জন্য add() পদ্ধতি , যেমন theQueue.add(10) ব্যবহার করে। PriorityQueue ক্লাসের কিছু কার্যকারিতা বোঝানোর জন্য , মেথড পিক() হিপের হেড খুঁজে বের করার জন্য ব্যবহার করা হয় এবং এটি হল সর্বাধিক মান, এই ক্ষেত্রে, 99। পরবর্তী কাজটি হল হিপের আকার পরীক্ষা করা। আকার ব্যবহার করে ()যা 9 পাওয়া যায় এবং এটি কনসোলে প্রিন্ট করা হয়। মেথড রাইটম্যাক্সহিপ সারিতে থাকা উপাদানগুলোকে রুট-এর ক্রমানুসারে লেখে, বাম-সন্তান রুট দিয়ে পিতা-মাতা, ডান-চাইল্ড রুট-এর সঙ্গে পিতা-মাতা, বাম-সন্তান প্রথম বাম-সন্তান অভিভাবক হিসাবে, ডান-সন্তান প্রথম বাম-সন্তান হিসাবে পিতামাতা, পিতামাতা হিসাবে প্রথম ডান-সন্তানের সাথে ডান-সন্তান, পিতামাতা হিসাবে প্রথম ডান-সন্তানের সাথে বাম-সন্তান ইত্যাদি, পরবর্তী মানগুলির সাথে বাম এবং ডান শিশুদের পিতামাতা হিসাবে একই ক্রমে ব্যবহার করে। একটি নির্দিষ্ট উপাদান, J, একটি সারিতে আছে কিনা তা খুঁজে বের করতে PriorityQueue পদ্ধতিতে ধারণ করে(J) ব্যবহার করা হয়। এই ক্ষেত্রে আমরা J = 10 সন্ধান করি। আমাদের উদাহরণে, এটি সত্য যে এটি সারিতে রয়েছে তাই এটি কনসোলে সত্য হিসাবে লেখা হয়েছে। আরেকটি অগ্রাধিকার সারি পদ্ধতি, remove(J) তারপর সারি থেকে J = 10 সরাতে ব্যবহৃত হয় । PriorityQueue- এর আরও কার্যকারিতা বোঝানোর জন্য , মেথড পোল() একটি while লুপ ব্যবহার করে হেড এলিমেন্ট (সর্বোচ্চ মান) অপসারণ করতে ব্যবহার করা হয় , প্রতিবার নতুন সারিতে হেড এলিমেন্টটি সরিয়ে ফেলা হয় এবং প্রতিবার সারির আকার এক করে কমানো হয়। এটি পদ্ধতি রাইট কিউতে ঘটেপ্রধান থেকে ডাকা হয়েছে। প্রতিবার সরানো উপাদানটি কনসোলে মুদ্রিত হয়। মূল সারিতে শেষ পর্যন্ত কোনো উপাদান অবশিষ্ট থাকবে না। মুদ্রিত উপাদানগুলি হল মূল্যের অবতরণ ক্রমে সর্বাধিক স্তূপ, যেখানে প্রতিবার সারির মাথাটি প্রিন্ট করা হয়।

mport java.util.Collections;
import java.util.PriorityQueue;

public class MaxHeap {

       public static void writeQueue(PriorityQueue<Integer> priorityQueue)
       {
           // Write out elements in queue, priorityQueue, and remove them using poll()
           while(priorityQueue.size() != 0)
           {
               System.out.println(priorityQueue.poll());
           }
       }

       public static void writeMaxHeap(PriorityQueue<Integer> priorityQueue)
       {
           // Write out elements in queue as a max heap - root, left child, right child, etc
           for (Integer element : priorityQueue) {
               System.out.println(element);
           }
       }

       public static void main(String args[])
       {
           // Array of numbers to create a max heap array from
           int[] theArray = {5, 3, 13, 10, 99, 19, 6, 51, 9};

           // theQueue is created
           PriorityQueue<Integer> theQueue =
                   new PriorityQueue<Integer>(Collections.reverseOrder());

           // Elements are added to theQueue
           for (int i = 0 ; i <theArray.length; ++i)
           {
               theQueue.add(theArray[i]);
           }

           // The head or root element (priority element) is printed out
           System.out.println("The root value is : " +  theQueue.peek());

           // Find size of theQueue. Use method size()
           Integer s = theQueue.size();
           System.out.println("Size of theQueue? " + s);

           // All elements of theQueue are printed in terms of parent,
           // left child, right child
           System.out.println("theQueue written using for loop:");
           writeMaxHeap(theQueue);

           // Does theQueue contain 10? Use method contains()
           boolean b = theQueue.contains(10);
           System.out.println("Does theQueue contain 10? " + b);

           // Erasing value 10 from array using remove()
           theQueue.remove(10);

           // All elements of theQueue are printed out and removed.
           // Each one is the maximum value left in the queue.
           // At the end theQueue will be empty
           System.out.println("theQueue written out using poll():");
           writeQueue(theQueue);

           // Find size of theQueue. Use method size()
           s = theQueue.size();
           System.out.println("Size of theQueue? " + s);
       }
   }

আউটপুট:

সর্বোচ্চ Heapify

সর্বোচ্চ হিপিফাই অ্যালগরিদমটি নিশ্চিত করতে ব্যবহৃত হয় যে একটি বাইনারি ট্রি একটি সর্বোচ্চ হিপ। যদি আমরা একটি নোড, n, এবং তার চাইল্ড নোড, বাম এবং ডান এছাড়াও হয় সর্বোচ্চ heaps নিজেদের, তারপর মহান, আমরা একটি সর্বোচ্চ গাদা আছে. যদি পুরো গাছ জুড়ে এটি না হয় তবে আমাদের সর্বাধিক গাদা নেই। ম্যাক্স হেপিফাই অ্যালগরিদম গাছটিকে সাজানোর জন্য ব্যবহার করা হয় যাতে এটি ম্যাক্সহিপ নীতিগুলি মেনে চলে। Max Heapify শুধুমাত্র একটি নোডে কাজ করে। যদি প্রয়োজন হয় যে অ্যারেটি একটি সর্বোচ্চ হিপ অ্যারে, তাহলে সমস্ত সাব ট্রিকে রুটের আগে ম্যাক্সহিপে রূপান্তর করতে হবে, একবারে একটি। প্রতিটি নোডে অ্যালগরিদম ব্যবহার করতে হবে। এটি N/2 নোডগুলিতে করা হবে (পাতাগুলি সর্বাধিক হিপ প্রয়োজনীয়তা মেনে চলবে)। হিপের সময় জটিলতা হল O(NlogN), এবং X উচ্চতায় একটি নোডের জন্য, সময়ের জটিলতা হল O(X)। নিম্নলিখিত কোড দেখায় কিভাবে একটি গাছ (একটি অ্যারে) maxheapify করতে হয়।

public class MaxHeapify

{
   public static Integer[] maxHeapify(Integer[ ] array, Integer i)
   {
       // Create left-child and right-child for the node in question
       Integer leftChild = 2 * i + 1;
       Integer rightChild = 2 * i + 2;

       // Assign maxVal to parent node, i
       Integer maxVal = i;

       // Set maxVal to greater of the two: node or left-child
       if( leftChild < array.length && array[leftChild] > array[maxVal] )
           maxVal = leftChild;

       // Set maxVal to greater of the two: maxVal or right-child
       if( rightChild < array.length && array[rightChild] > array[maxVal] )
           maxVal = rightChild;

       // Check if maxVal is not equal to parent node, then set parent node to
       // maxVal, swap values and then do a maxheapify on maxVal
       // which is now the previous parent node
       if( maxVal != i )
       {
           Integer value = array[i];
           array[i] = array[maxVal];
           array[maxVal] = value;
           array = maxHeapify(array, maxVal);
       }

       return array;
   }


   public static Integer[] maxHeapCreate(Integer array[])
   {
       // Call maxHeapify to arrange array in a max heap
       Integer [] theNewArr = array;
       for( Integer i = array.length/2; i >= 0; i-- )
           theNewArr = maxHeapify(array, i);

       return theNewArr;
   }

   public static void main(String[] args)
   {
       // Create array to be maxheapified, theArray,
       // and array, newArray, to write results into, by calling maxheapCreate
       // newArray will now be a maxheap
       Integer[] theArray = {5, 3, 13, 10, 99, 19, 6, 51, 9};
       Integer[ ] newArray = maxHeapCreate(theArray);

       // Print out contents of newArray
       System.out.println("newArray:");
       for(int i = 0; i < newArray.length; ++i)
       {
           System.out.println(newArray[i]);
       }

       // Print out labelled contents of newArray
       System.out.println(" root : " + newArray[0]);
       for (int i = 0; i <= newArray.length/2 - 1; i++) {
           System.out.print(" parent node : " + newArray[i] + " left child : " +
                            newArray[(2*i)+1] + " right child :" + newArray[(2*i)+2]);
           System.out.println();
       }
  }
}

আউটপুট প্রদান: এই কোডে, অ্যারে তৈরি করা হয় এবং সংখ্যা দিয়ে পূর্ণ হয়। একটি দ্বিতীয় অ্যারে, newArray , তৈরি করা হয়েছে এবং এবার এতে পদ্ধতির ফলাফল থাকবে, maxheapCreate , সর্বাধিক হিপ অ্যারে। মেথড maxHeapCreate কে main থেকে বলা হয় , এবং এখানে একটি নতুন অ্যারে, theNewArr , তৈরি করা হয় এবং maxHeapify ফলাফল দিয়ে পূর্ণ হয়। এটি ইনপুট অ্যারের অর্ধেক আকারের উপর লুপ করে করা হয়। লুপের প্রতিটি পাসের জন্য, পদ্ধতি maxHeapify , যাকে অ্যারের মাঝখানে উপাদান থেকে শুরু করে প্রথমটির সাথে শেষ করা হয়। maxHeapify- এর প্রতিটি কলের জন্য, প্যারেন্ট নোডের বাম শিশু এবং ডান সন্তান, i, পাওয়া যায় এবং তিনটির মধ্যে কোনটি সবচেয়ে বড় তা খুঁজে বের করার জন্য চেক করা হয়, এটিকে maxVal হিসাবে সংজ্ঞায়িত করে । যদি maxVal প্যারেন্ট নোডের সমান না হয় তবে একটি অদলবদল করা হয় যাতে প্যারেন্ট নোড এবং maxVal অদলবদল করা হয় এবং তারপর maxHeapify-কে এই বার maxVal- এ আবার কল করা হয় এবং আগের মতো একই পদক্ষেপগুলি চালানো হয়। অবশেষে সর্বাধিক হিপ তৈরি করা হবে এবং চালানোর জন্য আর কোনো পুনরাবৃত্তি হবে না। আপডেট করা অ্যারে, অ্যারে , এখন নতুন অ্যারে হিসাবে প্রধানে ফিরে আসে এবং তারপরে প্রতিটি পরপর উপাদান কনসোলে প্রিন্ট করা হয়। নতুন অ্যারেএখন একটি সর্বোচ্চ গাদা. দ্রষ্টব্য, অগ্রাধিকার সারি ব্যবহার করে আগের উদাহরণের মতো সংখ্যাগুলি লেখা হয়েছে: মূল, পিতামাতা হিসাবে মূলের ডান-সন্তান, পিতামাতা হিসাবে মূলের বাম-সন্তান, পিতামাতা হিসাবে প্রথম ডান-সন্তানের ডান-সন্তান, প্রথমের বাম-সন্তান বাবা-মা হিসাবে বাম-সন্তান, পিতা-মাতা হিসাবে প্রথম বাম-সন্তানের ডান-সন্তান, পিতা-মাতা হিসাবে প্রথম ডান-সন্তানের বাম-সন্তান, ইত্যাদি। তারা অগ্রাধিকার কিউ ব্যবহার করার সময় তাদের থেকে একটু ভিন্ন ক্রমে থাকে কারণ পরপর উপাদানগুলির মধ্যে তুলনা করা হয় যেখানে maxheapify উদাহরণে, নোডটিকে অ্যারের পরবর্তী দুটি ধারাবাহিক উপাদানের সাথে তুলনা করা হয় এবং সবচেয়ে বড় মানের জন্য অদলবদল করা হয়। সংক্ষেপে, দুটি ভিন্ন অ্যালগরিদম ব্যবহার করা হয়। উভয়ই একটি সর্বোচ্চ স্তূপ তৈরি করে।

উপসংহার

তাই এখানে আমরা সর্বোচ্চ হিপ দেখেছি এবং কিভাবে এটি একটি PriorityQueue বা একটি Max Heapify অ্যালগরিদম দিয়ে তৈরি করা যায়। reverseOrder() এর সাথে PriorityQueue ব্যবহার করা এটি করার একটি সুন্দর উপায় এবং প্রস্তাবিত পদ্ধতি। যাইহোক, আপনি এই উদাহরণগুলি অধ্যয়ন করতে পারেন এবং আপনার নিজের পদ্ধতিগুলি লিখতে পারেন কারণ এটি একটি ভাল কোডিং অনুশীলন হবে যা আপনাকে জাভা জুনিয়রের জন্য আপনার সাক্ষাত্কারে সফল হতে সহায়তা করবে।