জাভাতে র্যান্ডম সংখ্যা

1. সিউডোর্যান্ডম সংখ্যা

কখনও কখনও একজন প্রোগ্রামার আপাতদৃষ্টিতে সহজ কাজগুলির মুখোমুখি হন: "একটি নির্দিষ্ট তালিকা থেকে একটি এলোমেলো চলচ্চিত্র নির্বাচন করুন", "একটি লটারি বিজয়ী চয়ন করুন", "ব্যবহারকারী তার স্মার্টফোন নাড়ালে প্লেলিস্টটি এলোমেলো করুন", "একটি বার্তা এনক্রিপ্ট করতে একটি র্যান্ডম নম্বর চয়ন করুন" , ইত্যাদি। প্রতিটি ক্ষেত্রে, বিকাশকারী একটি যৌক্তিক প্রশ্ন জিজ্ঞাসা করে: কিভাবে একটি এলোমেলো নম্বর পেতে হয়?

প্রকৃতপক্ষে, সত্যিকারের র্যান্ডম নম্বর পাওয়া বেশ কঠিন। প্রকৃতপক্ষে, এটি এত কঠিন যে কিছু কম্পিউটারে বিশেষ গাণিতিক সহ-প্রসেসর তৈরি করা হয় যাতে এমন সংখ্যা তৈরি করা হয় যা সত্যিকারের এলোমেলোতার জন্য সমস্ত প্রয়োজনীয়তা পূরণ করে।

প্রোগ্রামাররা তাদের নিজস্ব সমাধান নিয়ে এসেছে: সিউডোর্যান্ডম সংখ্যা । সিউডোর্যান্ডম সংখ্যা হল এক ধরণের ক্রম, যার সংখ্যাগুলি এলোমেলো বলে মনে হয়। যাইহোক, একটি যত্নশীল বিশ্লেষণ সঞ্চালন করে, একজন বিশেষজ্ঞ অনুক্রমের নির্দিষ্ট নিদর্শন খুঁজে পেতে পারেন। এই ধরনের সংখ্যা গোপন নথি এনক্রিপ্ট করার জন্য উপযুক্ত নয়, কিন্তু তারা একটি খেলায় একটি ডাই রোল অনুকরণের জন্য যথেষ্ট।

সিউডোর্যান্ডম সংখ্যার একটি ক্রম তৈরি করার জন্য অনেক অ্যালগরিদম রয়েছে। তাদের প্রায় সকলেই পূর্ববর্তী সংখ্যা এবং কিছু অতিরিক্ত সহায়ক সংখ্যার উপর ভিত্তি করে পরবর্তী র্যান্ডম নম্বর তৈরি করে।

উদাহরণস্বরূপ, এই প্রোগ্রামটি 1000পুনরাবৃত্তি না হওয়া সংখ্যাগুলি প্রদর্শন করবে:

public class Main
{
   public static int a = 41;
   public static int c = 11119;
   public static int m = 11113;
   public static int seed = 1;

   public static int getNextRandom()
   {
     seed = (a * seed + c) % m;
     return seed;
   }

   public static void main(String[] args)
   {
     for (int i = 0; i < 1000; i++)
     {
       System.out.println(getNextRandom());
     }
   }
}

যাইহোক, আমরা এখানে সিউডোর্যান্ডম সংখ্যা সম্পর্কে কথা বলছি না। আমরা সিউডোর্যান্ডম সংখ্যার একটি ক্রম সম্পর্কে কথা বলছি। একটি একক সংখ্যা দেখে, এটি এলোমেলো কিনা তা বলা অসম্ভব।

প্রকৃতপক্ষে, একটি র্যান্ডম নম্বর পেতে বিভিন্ন উপায় আছে:

public static int getRandomNumber()
{
   return 4; // Here's a random number (we got it by rolling a die)
}

2.Math.random()

জাভাতে, Mathক্লাসের একটি বিশেষ পদ্ধতি রয়েছে যা একটি এলোমেলো সংখ্যা প্রদান করে। এবং আপনি অনুমান করতে পারেন, পদ্ধতি বলা হয় random. সাধারণভাবে, এই পদ্ধতিটিকে কল করার মতো দেখায়:

Math.random()

0এই পদ্ধতিতে কোন পরামিতি লাগে না এবং থেকে পর্যন্ত পরিসরে একটি ছদ্ম র্যান্ডম বাস্তব সংখ্যা প্রদান করে 1। সংখ্যা 1 নিজেই পরিসীমা অন্তর্ভুক্ত করা হয় না.

উদাহরণ:

public class Main
{
   public static void main(String[] args)
   {
     for (int i = 0; i < 10; i++)
     {
       System.out.println(Math.random());
     }
   }
}

0.9703753971734451
0.09979423801773157
0.994048474709053
0.2852203204171295
0.13551248551226025
0.3128547131272822
0.5342480554101412
0.6817369932044817
0.1840767788961758
0.06969563435451254

কিন্তু এই পদ্ধতিটি আপনার যা প্রয়োজন তা না হলে কী হবে? ধরুন, আপনি একটি প্রোগ্রাম লিখতে চান যা একটি ছয়-পার্শ্বযুক্ত ডাই রোলিং অনুকরণ করে। 0..1 পরিসরে বাস্তব সংখ্যার পরিবর্তে আপনি কীভাবে 1..6 পরিসরে র্যান্ডম পূর্ণসংখ্যা পাবেন?

এটা আসলে বেশ সহজ.

[0, 1)প্রথমত, আপনাকে পরিসরটি ম্যাপ করতে হবে [0, 6)। random()এটি করার জন্য, কেবল দ্বারা প্রত্যাবর্তিত ফলাফলটিকে গুন করুন 6। অবশ্যই, পূর্ণসংখ্যা পেতে, আপনাকে রাউন্ড আপ করতে হবে:

public class Main
{
   public static int getRandomDieNumber()
   {
      return (int) (Math.random() * 6);
   }

   public static void main(String[] args)
   {
      for (int i = 0; i < 10; i++)
      {
         int x = getRandomDieNumber();
         System.out.println(x);
      }
   }
}

5
2
3
3
2
4
1
1
5
0

getRandomDieNumber()সমেত পরিসরে একটি এলোমেলো পূর্ণসংখ্যা প্রদান করে 0..5। তবে সেটে এটি একটি সংখ্যা হবে না 1, 2, 3, 4, 5, 6। এটি সেটে একটি সংখ্যা হবে 0, 1, 2, 3, 4, 5।

আপনার যদি সেটের সংখ্যার প্রয়োজন হয় 1, 2, 3, 4, 5, 6, তাহলে শুধু এলোমেলো সংখ্যায় একটি যোগ করুন:

public class Main
{
   public static int getRandomDieNumber()
   {
      return (int) (Math.random() * 6) + 1;
   }

   public static void main(String[] args)
   {
     for (int i = 0; i < 10; i++)
     {
       int x = getRandomDieNumber();
       System.out.println(x);
     }
   }
}

3
2
1
3
6
5
6
1
6
6

এখন যে নিখুঁত!

3. Randomক্লাস

জাভাতে একটি বিশেষ Randomশ্রেণী রয়েছে যা সিউডোর্যান্ডম সংখ্যার একটি ক্রমকে অন্তর্ভুক্ত করে। আপনি ক্লাসের বিভিন্ন অবজেক্ট তৈরি করতে পারেন Random। এই বস্তুর প্রতিটি তার নিজস্ব সিউডোর্যান্ডম সংখ্যার ক্রম তৈরি করবে।

এটি অনেক আকর্ষণীয় পদ্ধতি সহ একটি সুপার আকর্ষণীয় ক্লাস। এর সবচেয়ে সহজ সঙ্গে শুরু করা যাক.

double nextDouble()

এই পদ্ধতিটি পরিসরে একটি এলোমেলো বাস্তব সংখ্যা প্রদান করে 0.0- 1.0। এটি Math.random()পদ্ধতির সাথে খুব মিল। এবং আশ্চর্যের কিছু নেই, যেহেতু Math.random()পদ্ধতিটি কেবল nextDouble()একটি Randomবস্তুর পদ্ধতিটিকে কল করে।

float nextFloat()

এই পদ্ধতিটি পদ্ধতির সাথে খুব মিল nextDouble(), কিন্তু ফিরে আসা এলোমেলো সংখ্যা হল একটি float। এটি পরিসরের মধ্যেও রয়েছে 0.0- 1.0. এবং, জাভাতে বরাবরের মতো, পরিসরটি সংখ্যাটি অন্তর্ভুক্ত করে না 1.0।

Random r = new Random();
float f = r.nextFloat();

int nextInt(int max)

এই পদ্ধতিটি পরিসরে একটি এলোমেলো পূর্ণসংখ্যা[0, max) প্রদান করে । 0সীমার মধ্যে অন্তর্ভুক্ত, কিন্তু maxনয়।

অন্য কথায়, আপনি যদি সেটটিতে একটি র্যান্ডম নম্বর পেতে চান 1, 2, 3, 4, 5, 6তবে আপনাকে ফিরে আসা র্যান্ডম নম্বরে একটি যোগ করতে হবে:

Random r = new Random();
int x = r.nextInt(6) + 1;

int nextInt()

এই পদ্ধতিটি আগেরটির মতোই, তবে এটি কোনও পরামিতি নেয় না। তাই তার রিটার্ন মান জন্য পরিসীমা কি? থেকে -2 billion। +2 billion_

ওয়েল, সুনির্দিষ্ট হতে, -2147483648থেকে +2147483647.

long nextLong()

এই পদ্ধতিটি পদ্ধতির অনুরূপ , কিন্তু রিটার্ন মান s nextInt()এর সম্পূর্ণ সম্ভাব্য পরিসরের কোথাও পড়বে ।long

boolean nextBoolean()

এই পদ্ধতিটি একটি এলোমেলো booleanমান প্রদান করে: falseবা true। এটি খুব সুবিধাজনক যখন আপনাকে র্যান্ডম বুলিয়ান মানগুলির একটি দীর্ঘ ক্রম পেতে হবে।

void nextBytes(byte[] data)

এই পদ্ধতিটি কিছুই ফেরত দেয় না (যেহেতু রিটার্ন টাইপ হল void)। পরিবর্তে, এটি র্যান্ডম মান দিয়ে পাস করা অ্যারে পূরণ করে। যখন আপনার এলোমেলো ডেটাতে ভরা একটি বড় বাফারের প্রয়োজন হয় তখন এটি খুব সহজ।

double nextGaussian()

এই পদ্ধতিটি পরিসরে একটি এলোমেলো বাস্তব সংখ্যা প্রদান করে 0.0- 1.0। যাইহোক, সংখ্যাগুলি এই পরিসরে সমানভাবে বিতরণ করা হয় না। পরিবর্তে, তারা একটি স্বাভাবিক বন্টন অনুসরণ করে ।

পরিসরের মাঝখানের মানগুলি ( 0.5) ব্যাপ্তির শেষে থাকা মানের চেয়ে বেশি ঘন ঘন ঘটবে৷

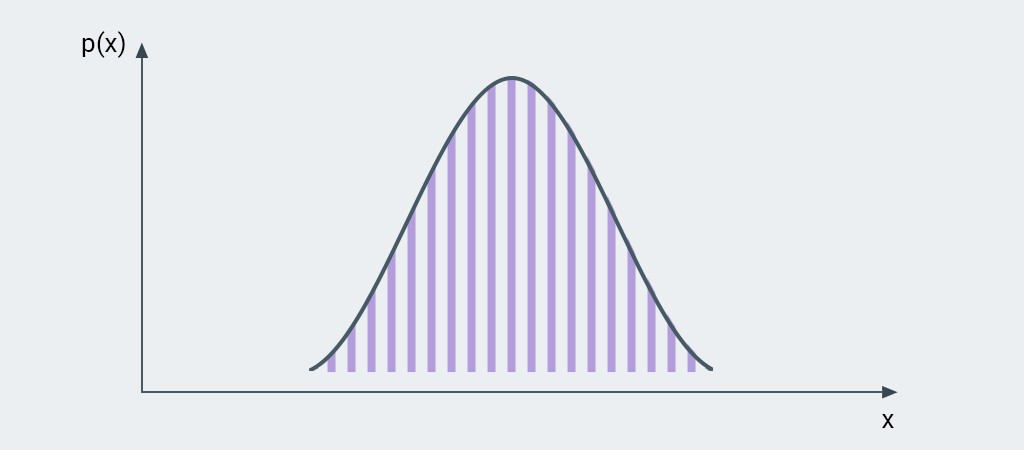
আমাদের ক্ষেত্রে, মান বন্টনের শীর্ষে থাকবে৷0.5