Tilfældige tal i Java

1. Pseudotilfældige tal

Nogle gange står en programmør over for tilsyneladende simple opgaver: "vælg en tilfældig film fra en bestemt liste", "vælg en lotterivinder", "bland afspilningslisten, når brugeren ryster sin smartphone", "vælg et tilfældigt tal for at kryptere en besked" osv. I hvert tilfælde stiller udvikleren et logisk spørgsmål: hvordan får man et tilfældigt tal?

Faktisk er det ret svært at få et tilfældigt tal. Faktisk er det så svært, at der er indbygget specielle matematiske coprocessorer i nogle computere for at generere tal, der opfylder alle kravene til ægte tilfældighed.

Programmører kom med deres egen løsning: pseudotilfældige tal . Pseudorandom-tal er en slags sekvens, hvis tal ser ud til at være tilfældige. Men ved at udføre en omhyggelig analyse kan en ekspert finde bestemte mønstre i sekvensen. Sådanne numre er ikke egnede til at kryptere hemmelige dokumenter, men de er tilstrækkelige til at simulere terningkast i et spil.

Der er mange algoritmer til at generere en sekvens af pseudotilfældige tal. Næsten alle af dem genererer det næste tilfældige tal baseret på det foregående tal og nogle ekstra hjælpernumre.

For eksempel vil dette program vise 1000ikke-gentagende tal:

public class Main
{
   public static int a = 41;
   public static int c = 11119;
   public static int m = 11113;
   public static int seed = 1;

   public static int getNextRandom()
   {
     seed = (a * seed + c) % m;
     return seed;
   }

   public static void main(String[] args)
   {
     for (int i = 0; i < 1000; i++)
     {
       System.out.println(getNextRandom());
     }
   }
}

Vi taler i øvrigt ikke om pseudorandom-tal her. Vi taler om en sekvens af pseudotilfældige tal. Ser man på et enkelt tal, er det umuligt at sige, om det er tilfældigt eller ej.

Faktisk er der forskellige måder at få et tilfældigt tal på:

public static int getRandomNumber()
{
   return 4; // Here's a random number (we got it by rolling a die)
}

2.Math.random()

I Java Mathhar klassen en speciel metode, der returnerer et tilfældigt tal. Og som du måske kan gætte, hedder metoden random. Generelt ser det ud her, at kalde denne metode:

Math.random()

Denne metode tager ingen parametre og returnerer et pseudotilfældigt reelt tal i intervallet fra 0til 1. Selve tallet 1 er ikke inkluderet i sortimentet.

Eksempel:

public class Main
{
   public static void main(String[] args)
   {
     for (int i = 0; i < 10; i++)
     {
       System.out.println(Math.random());
     }
   }
} 

0.9703753971734451
0.09979423801773157
0.994048474709053
0.2852203204171295
0.13551248551226025
0.3128547131272822
0.5342480554101412
0.6817369932044817
0.1840767788961758
0.06969563435451254

Men hvad hvis denne metode ikke er helt, hvad du har brug for? Antag, at du vil skrive et program, der simulerer at kaste en sekssidet terning. Hvordan får man tilfældige heltal i intervallet 1..6 i stedet for reelle tal i intervallet 0..1?

Det er faktisk ret simpelt.

Først skal du kortlægge rækkevidden [0, 1)på [0, 6). For at gøre dette skal du blot gange resultatet returneret med random()med 6. For at få heltal skal du selvfølgelig runde op:

public class Main
{
   public static int getRandomDieNumber()
   {
      return (int) (Math.random() * 6);
   }

   public static void main(String[] args)
   {
      for (int i = 0; i < 10; i++)
      {
         int x = getRandomDieNumber();
         System.out.println(x);
      }
   }
}

5
2
3
3
2
4
1
1
5
0

Returnerer getRandomDieNumber()et tilfældigt heltal i området 0..5inklusive. Men det bliver ikke et nummer i sættet 1, 2, 3, 4, 5, 6. Det vil være et nummer i sættet 0, 1, 2, 3, 4, 5.

Hvis det, du har brug for, er tal i sættet 1, 2, 3, 4, 5, 6, skal du bare tilføje et til de tilfældige tal:

public class Main
{
   public static int getRandomDieNumber()
   {
      return (int) (Math.random() * 6) + 1;
   }

   public static void main(String[] args)
   {
     for (int i = 0; i < 10; i++)
     {
       int x = getRandomDieNumber();
       System.out.println(x);
     }
   }
}

3
2
1
3
6
5
6
1
6
6

Nu er det perfekt!

3. Randomklasse

Java har en speciel Randomklasse, der indkapsler en sekvens af pseudotilfældige tal. Du kan oprette flere objekter i Randomklassen. Hvert af disse objekter vil generere sin egen sekvens af pseudorandom-numre.

Dette er en super interessant klasse med masser af interessante metoder. Lad os starte med det enkleste.

double nextDouble()

Denne metode returnerer et tilfældigt reelt tal i området 0.0- 1.0. Det minder meget om Math.random()metoden. Og ikke så mærkeligt, da Math.random()metoden blot kalder nextDouble()metoden på et Randomobjekt.

float nextFloat()

Denne metode minder meget om nextDouble()metoden, men det returnerede tilfældige tal er en float. Det ligger også i rækken 0.0- 1.0. Og som altid i Java inkluderer rækkevidden ikke 1.0selve tallet.

Random r = new Random();
float f = r.nextFloat();

int nextInt(int max)

Denne metode returnerer et tilfældigt heltal i området [0, max). 0er inkluderet i sortimentet, men maxer ikke.

Med andre ord, hvis du vil have et tilfældigt tal i sættet 1, 2, 3, 4, 5, 6, skal du tilføje et til det returnerede tilfældige tal:

Random r = new Random();
int x = r.nextInt(6) + 1;

int nextInt()

Denne metode ligner den forrige, men den tager ingen parametre. Så hvad er intervallet for dets returværdier? Fra -2 billiontil +2 billion.

Nå, for at være præcis, fra -2147483648til +2147483647.

long nextLong()

Denne metode ligner nextInt()metoden, men returværdien vil falde et sted i hele det mulige interval af longs.

boolean nextBoolean()

Denne metode returnerer en tilfældig booleanværdi: falseeller true. Dette er meget praktisk, når du har brug for at få en lang sekvens af tilfældige booleske værdier.

void nextBytes(byte[] data)

Denne metode returnerer intet (da returtypen er void). I stedet fylder den det beståede array med tilfældige værdier. Dette er meget praktisk, når du har brug for en stor buffer fyldt med tilfældige data.

double nextGaussian()

Denne metode returnerer et tilfældigt reelt tal i området 0.0- 1.0. Tallene er dog ikke ligeligt fordelt i dette interval. I stedet følger de en normalfordeling .

Værdier nær midten af ​​området ( 0.5) vil forekomme oftere end værdier i enderne af området.

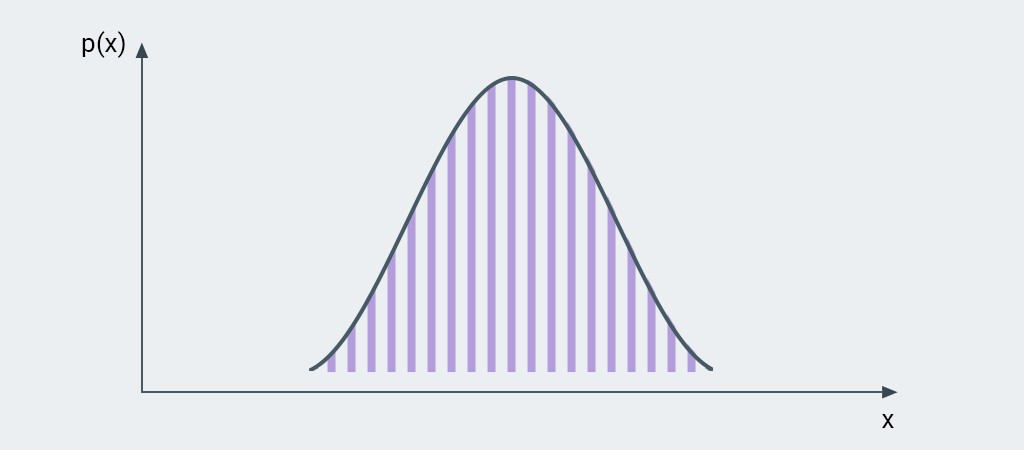
I vores tilfælde vil toppen af ​​værdifordelingen være kl0.5