Random numbers in Java

1. Pseudorandom numbers

Sometimes a programmer faces seemingly simple tasks: "select a random movie from a certain list", "choose a lottery winner", "shuffle the playlist when the user shakes his or her smartphone", "choose a random number to encrypt a message", etc. In each case, the developer asks a logical question: how to get a random number?

Actually, getting a truly random number is rather difficult to do. In fact, it is so difficult that special mathematical coprocessors are built into some computers in order to generate numbers that satisfy all the requirements for true randomness.

Programmers came up with their own solution: pseudorandom numbers. Pseudorandom numbers are a kind of sequence, whose numbers appear to be random. However, by performing a careful analysis, an expert can find certain patterns in the sequence. Such numbers are not suitable for encrypting secret documents, but they suffice for simulating the roll of a die in a game.

There are many algorithms for generating a sequence of pseudorandom numbers. Almost all of them generate the next random number based on the previous number and some additional helper numbers.

For example, this program will display 1000 non-repeating numbers:

public class Main
{
   public static int a = 41;
   public static int c = 11119;
   public static int m = 11113;
   public static int seed = 1;

   public static int getNextRandom()
   {
     seed = (a * seed + c) % m;
     return seed;
   }

   public static void main(String[] args)
   {
     for (int i = 0; i < 1000; i++)
     {
       System.out.println(getNextRandom());
     }
   }
}

By the way, we're not talking about pseudorandom numbers here. We're talking about a sequence of pseudorandom numbers. Looking at a single number, it is impossible to tell whether it is random or not.

Indeed, there are various ways to get a random number:

public static int getRandomNumber()
{
   return 4; // Here's a random number (we got it by rolling a die)
}

2. Math.random()

In Java, the Math class has a special method that returns a random number. And as you might guess, the method is called random. In general, here is what it looks like to call this method:

Math.random()

This method takes no parameters and returns a pseudorandom real number in the range from 0 to 1. The number 1 itself is not included in the range.

Example:

public class Main
{
   public static void main(String[] args)
   {
     for (int i = 0; i < 10; i++)
     {
       System.out.println(Math.random());
     }
   }
} 

0.9703753971734451
0.09979423801773157
0.994048474709053
0.2852203204171295
0.13551248551226025
0.3128547131272822
0.5342480554101412
0.6817369932044817
0.1840767788961758
0.06969563435451254

But what if this method isn't quite what you need? Suppose, you want to write a program that simulates rolling a six-sided die. How do you get random integers in the range 1..6, instead of real numbers in the range 0..1?

It's actually pretty simple.

First, you need to map the range [0, 1) onto [0, 6). To do this, simply multiply the result returned by random() by 6. Of course, to get integers, you need to round up:

public class Main
{
   public static int getRandomDieNumber()
   {
      return (int) (Math.random() * 6);
   }

   public static void main(String[] args)
   {
      for (int i = 0; i < 10; i++)
      {
         int x = getRandomDieNumber();
         System.out.println(x);
      }
   }
}

5
2
3
3
2
4
1
1
5
0

The getRandomDieNumber() returns a random integer in the range 0..5 inclusive. But it will not be a number in the set 1, 2, 3, 4, 5, 6. It will be a number in the set 0, 1, 2, 3, 4, 5.

If what you need is numbers in the set 1, 2, 3, 4, 5, 6, then just add one to the random numbers:

public class Main
{
   public static int getRandomDieNumber()
   {
      return (int) (Math.random() * 6) + 1;
   }

   public static void main(String[] args)
   {
     for (int i = 0; i < 10; i++)
     {
       int x = getRandomDieNumber();
       System.out.println(x);
     }
   }
}

3
2
1
3
6
5
6
1
6
6

Now that's perfect!

9

Task

New Java Syntax, level 9, lesson 2

Locked

Octal converter

The public static toOctal(int) method must convert the integer received as an input parameter from the decimal numeral system into octal. And conversely, the public static toDecimal(int) method converts from the octal system into decimal. The methods only work with positive numbers. If the input par

Open

3. Random class

Java has a special Random class that encapsulates a sequence of pseudorandom numbers. You can create several objects of the Random class. Each of these objects will generate its own sequence of pseudorandom numbers.

This is a super interesting class with lots of interesting methods. Let's start with the simplest.

double nextDouble()

This method returns a random real number in the range 0.0-1.0. It is very similar to the Math.random() method. And no wonder, since the Math.random() method simply calls the nextDouble() method on a Random object.

float nextFloat()

This method is very similar to the nextDouble() method, but the returned random number is a float. It also lies in the range 0.0-1.0. And, as always in Java, the range does not include the number 1.0 itself.

Random r = new Random();
float f = r.nextFloat();

int nextInt(int max)

This method returns a random integer in the range [0, max). 0 is included in the range, but max is not.

In other words, if you want to get a random number in the set 1, 2, 3, 4, 5, 6, then you need to add one to the returned random number:

Random r = new Random();
int x = r.nextInt(6) + 1;

int nextInt()

This method is similar to the previous one, but it does not take any parameters. So what is the range for its return values? From -2 billion to +2 billion.

Well, to be precise, from -2147483648 to +2147483647.

long nextLong()

This method is similar to the nextInt() method, but the return value will fall somewhere in the entire possible range of longs.

boolean nextBoolean()

This method returns a random boolean value: false or true. This is very convenient when you need to get a long sequence of random boolean values.

void nextBytes(byte[] data)

This method returns nothing (since the return type is void). Instead, it fills the passed array with random values. This is very handy when you need a large buffer filled with random data.

double nextGaussian()

This method returns a random real number in the range 0.0-1.0. However, the numbers are not evenly distributed in this range. Instead, they follow a normal distribution.

Values near the middle of the range (0.5) will occur more often than values at the ends of the range.

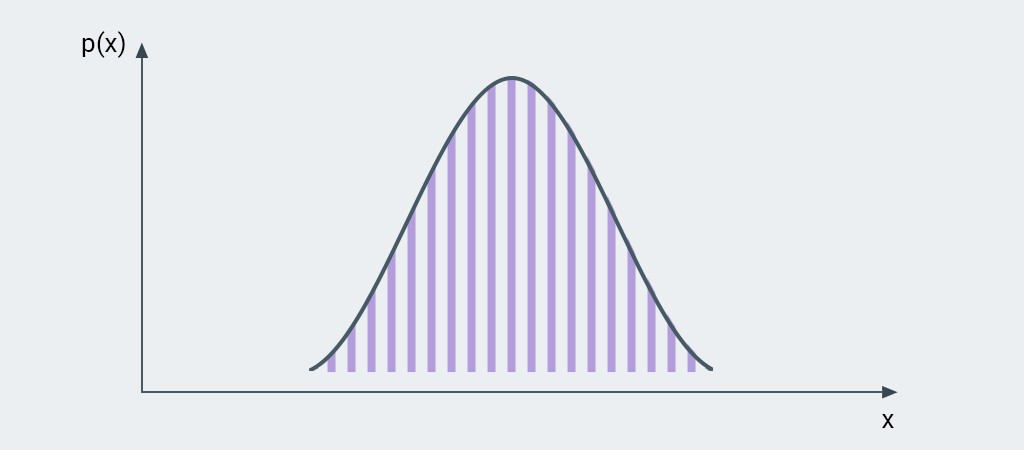
In our case, the peak of the value distribution will be at 0.5

9

Task

New Java Syntax, level 9, lesson 2

Locked

Binary converter

The public static toBinary(int) method must convert the integer received as an input parameter from the decimal numeral system to binary and return its string representation. And conversely, the public static toDecimal(String) method converts from the string representation of a binary number to a de

Open

9

Task

New Java Syntax, level 9, lesson 2

Locked

Hexadecimal converter

The public static toHex(String) method must convert the integer received as an input parameter from the decimal numeral system to hexadecimal and return its string representation. And conversely, the public static toDecimal(String) method converts from the string representation of a hexadecimal numb

Open

9

Task

New Java Syntax, level 9, lesson 2

Locked

Binary to hexadecimal converter

The public static toHex(String) method must convert the string representation of a binary number, received as an input parameter, from the binary numeral system to hexadecimal and return its string representation. And conversely, the public static toBinary(String) method converts from the string rep

Open