 Ngayon ay pag-uusapan natin ang tungkol sa mga graph at ang mga algorithm na nauugnay sa kanila. Ang graph ay isa sa mga pinaka-flexible at versatile na istruktura sa programming. Ang graph G ay karaniwang tinutukoy ng isang pares ng mga set, ibig sabihin, G = (V, R), kung saan:
Ngayon ay pag-uusapan natin ang tungkol sa mga graph at ang mga algorithm na nauugnay sa kanila. Ang graph ay isa sa mga pinaka-flexible at versatile na istruktura sa programming. Ang graph G ay karaniwang tinutukoy ng isang pares ng mga set, ibig sabihin, G = (V, R), kung saan:
- Ang V ay isang hanay ng mga vertex;
- Ang R ay isang hanay ng mga linya na nagdudugtong sa mga pares ng mga vertex.
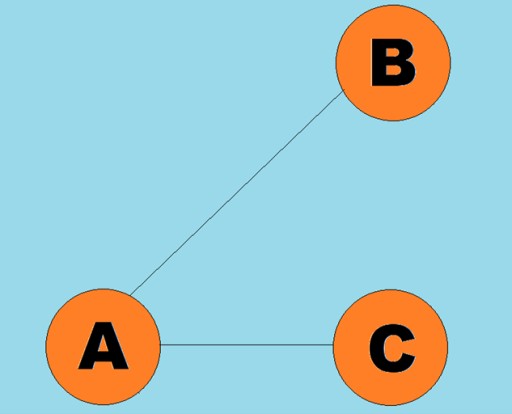 Tinatawag na mga arko ang mga nakadirekta na linya:
Tinatawag na mga arko ang mga nakadirekta na linya: 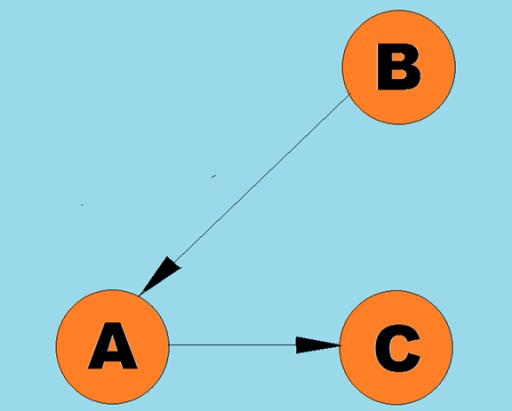 Karaniwan, ang isang graph ay kinakatawan ng isang diagram kung saan ang ilan sa mga vertices ay konektado sa pamamagitan ng mga gilid (mga arko). Ang mga graph na ang mga gilid ay nagsasaad ng direksyon ng traversal ay tinatawag na directed graphs. Kung ang isang graph ay konektado sa pamamagitan ng mga gilid na hindi nagpapahiwatig ng direksyon ng traversal, pagkatapos ay sinasabi namin na ito ay isang hindi nakadirekta na graph. Nangangahulugan ito na ang paggalaw ay posible sa parehong direksyon: parehong mula sa vertex A hanggang sa vertex B, at mula sa vertex B hanggang sa vertex A. Ang konektadong graph ay isang graph kung saan hindi bababa sa isang landas ang humahantong mula sa bawat vertex patungo sa anumang iba pang vertex (tulad ng sa halimbawa sa itaas). Kung hindi ito ang kaso, ang graph ay sinasabing nadiskonekta:
Karaniwan, ang isang graph ay kinakatawan ng isang diagram kung saan ang ilan sa mga vertices ay konektado sa pamamagitan ng mga gilid (mga arko). Ang mga graph na ang mga gilid ay nagsasaad ng direksyon ng traversal ay tinatawag na directed graphs. Kung ang isang graph ay konektado sa pamamagitan ng mga gilid na hindi nagpapahiwatig ng direksyon ng traversal, pagkatapos ay sinasabi namin na ito ay isang hindi nakadirekta na graph. Nangangahulugan ito na ang paggalaw ay posible sa parehong direksyon: parehong mula sa vertex A hanggang sa vertex B, at mula sa vertex B hanggang sa vertex A. Ang konektadong graph ay isang graph kung saan hindi bababa sa isang landas ang humahantong mula sa bawat vertex patungo sa anumang iba pang vertex (tulad ng sa halimbawa sa itaas). Kung hindi ito ang kaso, ang graph ay sinasabing nadiskonekta: 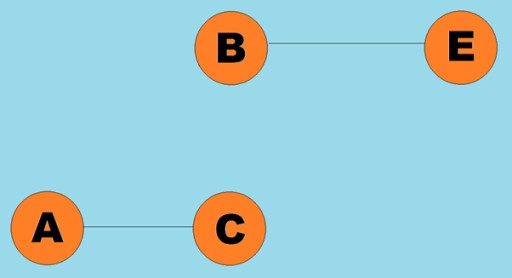 Ang mga timbang ay maaari ding italaga sa mga gilid (mga arko). Ang mga timbang ay mga numero na kumakatawan, halimbawa, ang pisikal na distansya sa pagitan ng dalawang vertice (o ang kaugnay na oras ng paglalakbay sa pagitan ng dalawang vertices). Ang mga graph na ito ay tinatawag na weighted graphs:
Ang mga timbang ay maaari ding italaga sa mga gilid (mga arko). Ang mga timbang ay mga numero na kumakatawan, halimbawa, ang pisikal na distansya sa pagitan ng dalawang vertice (o ang kaugnay na oras ng paglalakbay sa pagitan ng dalawang vertices). Ang mga graph na ito ay tinatawag na weighted graphs: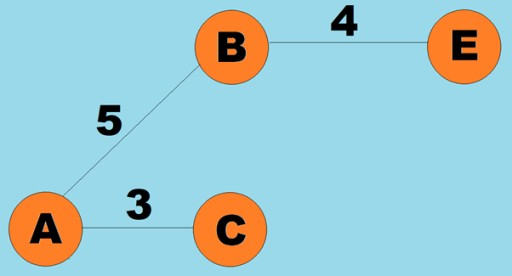
3. Pathfinding algorithm (depth-first, breadth-first)
Ang isa sa mga pangunahing operasyong isinagawa gamit ang mga graph ay ang pagtukoy sa lahat ng mga vertex na maaabot mula sa isang naibigay na vertex. Isipin na sinusubukan mong tukuyin kung paano ka makakasakay ng bus mula sa isang lungsod patungo sa isa pa, kabilang ang mga posibleng paglipat. Ang ilang mga lungsod ay maaaring direktang maabot, habang ang ilan ay maaari lamang maabot sa pamamagitan ng pagdaan sa ibang mga lungsod. Mayroong maraming iba pang mga sitwasyon kung saan maaaring kailanganin mong hanapin ang lahat ng mga vertex na maaari mong maabot mula sa isang naibigay na vertex. Mayroong dalawang pangunahing paraan upang tumawid sa mga graph: depth-first at breadth-first. Tuklasin natin ang dalawang ito. Ang parehong mga pamamaraan ay dumadaan sa lahat ng konektadong vertices. Upang higit pang tuklasin ang depth-first at breadth-first algorithm, gagamitin namin ang sumusunod na graph:
Malalim-unang paghahanap
Ito ay isa sa mga pinakakaraniwang paraan ng pag-travers ng graph. Ang diskarte sa depth-first ay pumunta nang mas malalim hangga't maaari sa isang graph. Pagkatapos, pagkatapos maabot ang isang dead end, babalik tayo sa pinakamalapit na vertex na dati nang hindi nabisitang mga katabing vertex. Ang algorithm na ito ay nag-iimbak ng impormasyon sa stack tungkol sa kung saan babalik kapag naabot ang isang dead-end. Mga panuntunan para sa malalim na paghahanap:- Bisitahin ang isang hindi pa nabisitang katabing vertex, markahan ito bilang binisita, at itulak ito sa stack.
- Lumipat sa tuktok na ito.
- Ulitin ang hakbang 1.
- Kung imposible ang hakbang 1, bumalik sa nakaraang vertex at subukang gawin ang hakbang 1. Kung hindi iyon posible, bumalik sa vertex bago iyon, at iba pa, hanggang sa makakita tayo ng vertex kung saan maaari nating ipagpatuloy ang traversal.
- Magpatuloy hanggang ang lahat ng vertices ay nasa stack.
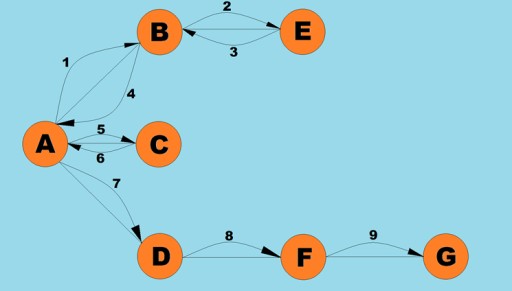 Tingnan natin kung ano ang maaaring hitsura ng Java code para sa algorithm na ito:
Tingnan natin kung ano ang maaaring hitsura ng Java code para sa algorithm na ito:
public class Graph {
private final int MAX_VERTS = 10;
private Vertex vertexArray[]; // Array of vertices
private int adjMat[][]; // Adjacency matrix
private int nVerts; // Current number of vertices
private Stack stack;
public Graph() { // Initialize internal fields
vertexArray = new Vertex[MAX_VERTS];
adjMat = new int[MAX_VERTS][MAX_VERTS];
nVerts = 0;
for (int j = 0; j < MAX_VERTS; j++) {
for (int k = 0; k < MAX_VERTS; k++) {
adjMat[j][k] = 0;
}
}
stack = new Stack<>();
}
public void addVertex(char lab) {
vertexArray[nVerts++] = new Vertex(lab);
}
public void addEdge(int start, int end) {
adjMat[start][end] = 1;
adjMat[end][start] = 1;
}
public void displayVertex(int v) {
System.out.println(vertexArray[v].getLabel());
}
public void dfs() { // Depth-first search
vertexArray[0].setVisited(true); // Take the first vertex
displayVertex(0);
stack.push(0);
while (!stack.empty()) {
int v = getAdjUnvisitedVertex(stack.peek()); // Return the index of the adjacent vertex: if any, 1; if not, -1
if (v == -1) { // If there is no unvisited adjacent vertex
stack.pop(); // The element is removed from the stack
}
else {
vertexArray[v].setVisited(true);
displayVertex(v);
stack.push(v); // The element goes on top of the stack
}
}
for (int j = 0; j < nVerts; j++) { // Reset the flags
vertexArray[j].visited = false;
}
}
private int getAdjUnvisitedVertex(int v) {
for (int j = 0; j < nVerts; j++) {
if (adjMat[v][j] == 1 && vertexArray[j].visited == false) {
return j; // Returns the first vertex found
}
}
return -1;
}
}public class Vertex {
private char label; // for example, 'A'
public boolean visited;
public Vertex(final char label) {
this.label = label;
visited = false;
}
public char getLabel() {
return this.label;
}
public boolean isVisited() {
return this.visited;
}
public void setVisited(final boolean visited) {
this.visited = visited;
}
}public class Solution {
public static void main(String[] args) {
Graph graph = new Graph();
graph.addVertex('A'); //0
graph.addVertex('B'); //1
graph.addVertex('C'); //2
graph.addVertex('D'); //3
graph.addVertex('E'); //4
graph.addVertex('F'); //5
graph.addVertex('G'); //6
graph.addEdge(0,1);
graph.addEdge(0,2);
graph.addEdge(0,3);
graph.addEdge(1,4);
graph.addEdge(3,5);
graph.addEdge(5,6);
System.out.println("Visits: ");
graph.dfs();
}
}Breadth-first search
Tulad ng depth-first na paghahanap, ang algorithm na ito ay isa sa pinakasimple at pinakapangunahing paraan ng pagtawid ng graph. Ang diwa ay mayroon kaming ilang kasalukuyang vertex. Inilalagay namin ang lahat ng hindi nabisitang katabing vertice nito sa isang queue at piliin ang susunod na elemento (na ang vertex na naka-imbak sa ulo ng queue), na nagiging kasalukuyang vertex... Paghiwa-hiwalayin ang algorithm na ito sa mga yugto, matutukoy namin ang mga sumusunod na hakbang:- Bisitahin ang susunod na dati nang hindi nabisitang vertex na katabi ng kasalukuyang vertex, markahan ito bilang binisita nang maaga, at idagdag ito sa queue.
- Kung hindi maisagawa ang hakbang #1, pagkatapos ay alisin ang vertex mula sa pila at gawin itong kasalukuyang vertex.
- Kung hindi maisagawa ang mga hakbang #1 at #2, tapos na tayo sa pagtawid — bawat vertex ay nalampasan na (kung mayroon tayong konektadong graph).
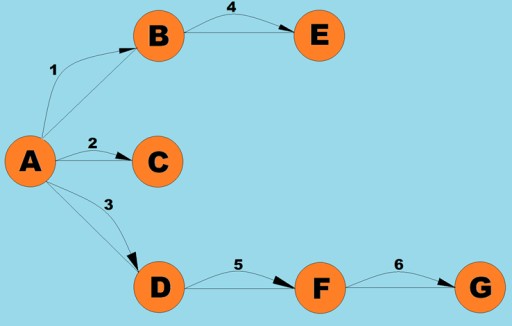 Ang graph class dito ay halos magkapareho sa ginamit namin para sa depth-first search algorithm, maliban sa mismong paraan ng paghahanap at ang katotohanang pinapalitan ng queue ang internal stack:
Ang graph class dito ay halos magkapareho sa ginamit namin para sa depth-first search algorithm, maliban sa mismong paraan ng paghahanap at ang katotohanang pinapalitan ng queue ang internal stack:
public class Graph {
private final int MAX_VERTS = 10;
private Vertex vertexList[]; // Array of vertices
private int adjMat[][]; // Adjacency matrix
private int nVerts; // Current number of vertices
private Queue queue;
public Graph() {
vertexList = new Vertex[MAX_VERTS];
adjMat = new int[MAX_VERTS][MAX_VERTS];
nVerts = 0;
for (int j = 0; j < MAX_VERTS; j++) {
for (int k = 0; k < MAX_VERTS; k++) { // Fill the adjacency matrix with zeros
adjMat[j][k] = 0;
}
}
queue = new PriorityQueue<>();
}
public void addVertex(char lab) {
vertexList[nVerts++] = new Vertex(lab);
}
public void addEdge(int start, int end) {
adjMat[start][end] = 1;
adjMat[end][start] = 1;
}
public void displayVertex(int v) {
System.out.println(vertexList[v].getLabel());
}
public void bfc() { // Depth-first search
vertexList[0].setVisited(true);
displayVertex(0);
queue.add(0);
int v2;
while (!queue.isEmpty()) {
int v = queue.remove();
while((v2 = getAdjUnvisitedVertex(v))!=-1) {// The loop runs until every adjacent vertex is found and added to the queue
vertexList[v2].visited = true;
displayVertex(v2);
queue.add(v2);
}
}
for (int j = 0; j < nVerts; j++) { // Reset the flags
vertexList[j].visited = false;
}
}
private int getAdjUnvisitedVertex(int v) {
for (int j = 0; j < nVerts; j++) {
if (adjMat[v][j] == 1 && vertexList[j].visited == false) {
return j; // Returns the first vertext found
}
}
return -1;
}
}public class Solution {
public static void main(String[] args) {
Graph graph = new Graph();
graph.addVertex('A'); //0
graph.addVertex('B'); //1
graph.addVertex('C'); //2
graph.addVertex('D'); //3
graph.addVertex('E'); //4
graph.addVertex('F'); //5
graph.addVertex('G'); //6
graph.addEdge(0,1);
graph.addEdge(0,2);
graph.addEdge(0,3);
graph.addEdge(1,4);
graph.addEdge(3,5);
graph.addEdge(5,6);
System.out.println("Visits: ");
graph.bfc();
}
}4. Algoritmo ni Dijkstra
Tulad ng nabanggit kanina, ang mga graph ay maaaring idirekta o hindi idirekta. At maaalala mo na maaari rin silang timbangin. Ang mga may timbang at nakadirekta na mga graph ay nagmodelo ng mga ugnayang madalas na makikita sa totoong buhay: halimbawa, isang mapa ng mga lungsod kung saan ang mga lungsod ay vertices, at ang mga gilid sa pagitan ng mga ito ay mga kalsadang may one-way na trapiko, na dumadaloy sa direksyon ng nakadirekta na gilid. Sabihin nating isa kang kumpanya ng kargamento at kailangan mong hanapin ang pinakamaikling ruta sa pagitan ng dalawang malalayong lungsod. Paano mo ito gagawin? Ang paghahanap ng pinakamaikling landas sa pagitan ng dalawang vertice ay isa sa mga pinakakaraniwang problema na nalutas gamit ang mga weighted graph. Upang malutas ang problemang ito, ginagamit namin ang algorithm ng Dijkstra. Sa sandaling patakbuhin mo ito, malalaman mo ang pinakamaikling landas mula sa isang naibigay na paunang tuktok sa bawat isa. Ano ang mga hakbang ng algorithm na ito? Susubukan kong sagutin ang tanong na ito. Mga hakbang ng algorithm ng Dijkstra:- Hakbang 1: Hanapin ang katabing node na may pinakamababang gastos upang mag-navigate (pinakamababang timbang sa gilid). Nakatayo ka sa pinakadulo simula at iniisip kung saan pupunta: sa node A o node B. Magkano ang halaga ng paglipat sa bawat isa sa mga node na ito?
- Hakbang 2: kalkulahin ang distansya upang maglakbay sa lahat ng mga kapitbahay ng node В na hindi pa napupuntahan ng algorithm kapag binabagtas ang gilid mula sa В. Kung ang bagong distansya ay mas mababa kaysa sa luma, ang landas sa gilid B ay magiging bagong pinakamaikling landas para sa vertex na ito.
- Hakbang 3: markahan ang vertex B bilang binisita.
- Hakbang 4: Pumunta sa hakbang 1.
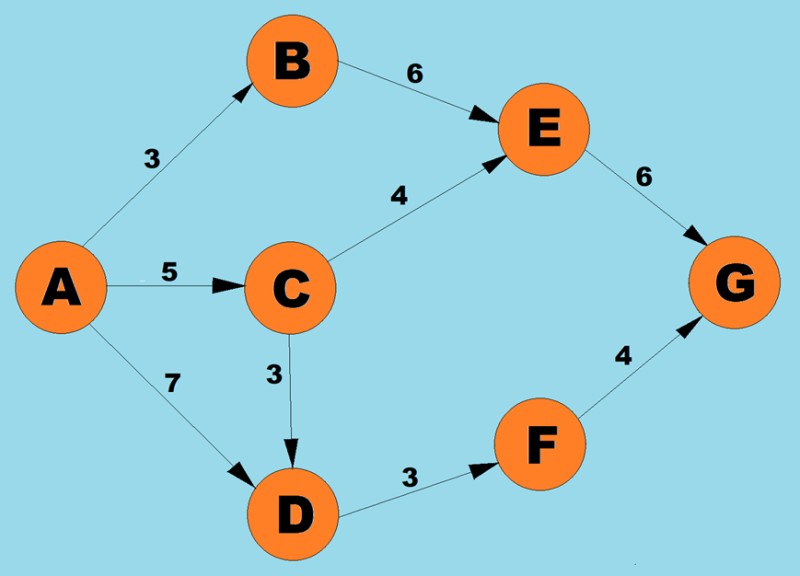 Gamit ang algorithm sa itaas, tutukuyin natin ang pinakamaikling landas mula A hanggang G:
Gamit ang algorithm sa itaas, tutukuyin natin ang pinakamaikling landas mula A hanggang G:
- Mayroong tatlong posibleng mga landas para sa vertex A: hanggang B na may timbang 3, hanggang С na may timbang 5, at sa D na may timbang 7. Ayon sa unang hakbang ng algorithm, pipiliin namin ang node na may pinakamababang gastos (timbang ng gilid). Sa kasong ito, si B.
-
Dahil ang tanging hindi nabisitang kapitbahay ni B ay ang vertex Е, tinitingnan namin kung ano ang magiging landas kung dumaan kami sa tuktok na ito. 3(AB) + 6(BE) = 9.
Kaya, naitala namin na ang kasalukuyang pinakamaikling landas mula A hanggang E ay 9.
-
Dahil kumpleto na ang aming trabaho sa vertex B, magpapatuloy kami sa pagpili ng susunod na vertex na may pinakamababang timbang ang gilid.
Mula sa vertices A at B, ang mga posibilidad ay vertices D (7), C (5), o E (6).
Ang gilid sa С ay may pinakamaliit na timbang, kaya pumunta kami sa tuktok na ito.
-
Susunod, tulad ng dati, nahanap namin ang pinakamaikling landas sa mga kalapit na vertice kapag dumadaan sa C:
-
AD = 5 (AC) + 3 (CD) = 8, ngunit dahil ang nakaraang pinakamaikling landas (AC = 7) ay mas mababa kaysa sa isang ito hanggang sa С, pinapanatili namin ang pinakamaikling landas (AC = 7) na hindi nagbabago.
-
CE = 5(AC) + 4(CE) = 9. Ang bagong pinakamaikling landas na ito ay katumbas ng nauna, kaya hinahayaan din namin itong hindi nagbabago.
-
-
Mula sa pinakamalapit na naa-access na vertices (E at D), piliin ang vertex na may pinakamaliit na gilid na timbang, ibig sabihin, D (3).
-
Nahanap namin ang pinakamaikling landas patungo sa kapitbahay nitong F.
AF = 7(AD) + 3(DF) = 9
-
Mula sa pinakamalapit na naa-access na vertices (E at F), piliin ang vertex na may pinakamaliit na gilid na timbang, ibig sabihin, F (3).
-
Hanapin ang pinakamaikling daan patungo sa kapitbahay nito na si G.
AG = 7(AD) + 3(DF) + 4(FG) = 14
Kaya, nakahanap kami ng landas mula A hanggang G.
Ngunit upang matiyak na ito ang pinakamaikling, dapat din nating gawin ang ating mga hakbang sa vertex E.
-
Dahil ang vertex G ay walang mga kalapit na vertice na itinuturo ng mga nakadirekta na gilid, mayroon na lang tayong vertex E na natitira, kaya pipiliin natin ito.
-
Hanapin ang pinakamaikling daan patungo sa kapitbahay na si G.
AG = 3 (AB) + 6 (BE) + 6 (EG) = 15. Ang landas na ito ay mas mahaba kaysa sa nakaraang pinakamaikling landas (AG (14)), kaya iniiwan namin ang landas na ito nang hindi nagbabago.
Dahil walang mga vertex na humahantong mula sa G, walang saysay na patakbuhin ang mga hakbang sa algorithm sa vertex na ito. Ibig sabihin, kumpleto na ang gawain ng algorithm.
public class Vertex {
private char label;
private boolean isInTree;
public Vertex(char label) {
this.label = label;
this.isInTree = false;
}
public char getLabel() {
return label;
}
public void setLabel(char label) {
this.label = label;
}
public boolean isInTree() {
return isInTree;
}
public void setInTree(boolean inTree) {
isInTree = inTree;
}
}public class Path { // A class that contains the distance and the previous and traversed vertices
private int distance; // Current distance from the starting vertex
private List parentVertices; // Current parent vertex
public Path(int distance) {
this.distance = distance;
this.parentVertices = new ArrayList<>();
}
public int getDistance() {
return distance;
}
public void setDistance(int distance) {
this.distance = distance;
}
public List getParentVertices() {
return parentVertices;
}
public void setParentVertices(List parentVertices) {
this.parentVertices = parentVertices;
}
}public class Graph {
private final int MAX_VERTS = 10;// Maximum number of vertices
private final int INFINITY = 100000000; // This number represents infinity
private Vertex vertexList[]; // List of vertices
private int relationMatrix[][]; // Matrix of edges between vertices
private int numberOfVertices; // Current number of vertices
private int numberOfVerticesInTree; // Number of visited vertices in the tree
private List shortestPaths; // List of shortest paths
private int currentVertex; // Current vertex
private int startToCurrent; // Distance to currentVertex
public Graph() {
vertexList = new Vertex[MAX_VERTS]; // Adjacency matrix
relationMatrix = new int[MAX_VERTS][MAX_VERTS];
numberOfVertices = 0;
numberOfVerticesInTree = 0;
for (int i = 0; i < MAX_VERTS; i++) { // Fill the adjacency matrix
for (int k = 0; k < MAX_VERTS; k++) { // with "infinity"
relationMatrix[i][k] = INFINITY; // Assign default values
shortestPaths = new ArrayList<>(); // Assign an empty list
}
}
}
public void addVertex(char lab) {// Assign new vertices
vertexList[numberOfVertices++] = new Vertex(lab);
}
public void addEdge(int start, int end, int weight) {
relationMatrix[start][end] = weight; // Set weighted edges between vertices
}
public void path() { // Choose the shortest path
// Set the initial vertex data
int startTree = 0; // Start from vertex 0
vertexList[startTree].setInTree(true); // Include the first element in the tree
numberOfVerticesInTree = 1;
// Fill out the shortest paths for vertices adjacent to the initial vertex
for (int i = 0; i < numberOfVertices; i++) {
int tempDist = relationMatrix[startTree][i];
Path path = new Path(tempDist);
path.getParentVertices().add(0);// The starting vertex will always be a parent vertex
shortestPaths.add(path);
}
// Until every vertex is in the tree
while (numberOfVerticesInTree < numberOfVertices) { // Do this until the number of of vertices in the tree equals the total number of vertices
int indexMin = getMin();// Get the index of the of the vertex with the smallest distance from the vertices not yet in the tree
int minDist = shortestPaths.get(indexMin).getDistance(); // Minimum distance to the vertices not yet in the tree
if (minDist == INFINITY) {
System.out.println("The graph has an unreachable vertex");
break; // If only unreachable vertices have not been visited, then we exit the loop
} else {
currentVertex = indexMin; // Set currentVert to the index of the current vertex
startToCurrent = shortestPaths.get(indexMin).getDistance(); // Set the distance to the current vertex
}
vertexList[currentVertex].setInTree(true); // Add the current vertex to the tree
numberOfVerticesInTree++; // Increase the count of vertices in the tree
updateShortestPaths(); // Update the list of shortest paths
}
displayPaths(); // Display the results on the console
}
public void clear() { // Clear the tree
numberOfVerticesInTree = 0;
for (int i = 0; i < numberOfVertices; i++) {
vertexList[i].setInTree(false);
}
}
private int getMin() {
int minDist = INFINITY; // The distance of the initial shortest path is taken to be infinite
int indexMin = 0;
for (int i = 1; i < numberOfVertices; i++) { // For each vertex
if (!vertexList[i].isInTree() && shortestPaths.get(i).getDistance() < minDist) { // If the vertex is not yet in the tree and the distance to the vertex is less than the current minimum
minDist = shortestPaths.get(i).getDistance(); // then update the minimum
indexMin = i; // Update the index of the vertex with the minimum distance
}
}
return indexMin; // Returns the index of the vertex with the smallest distance among those not yet in the tree
}
private void updateShortestPaths() {
int vertexIndex = 1; // The initial vertex is skipped
while (vertexIndex < numberOfVertices) { // Run over the columns
if (vertexList[vertexIndex].isInTree()) { // If the column vertex is already in the tree, then we skip it
vertexIndex++;
continue;
}
// Calculate the distance for one element sPath
// Get the edge from currentVert to column
int currentToFringe = relationMatrix[currentVertex][vertexIndex];
// Add up all the distances
int startToFringe = startToCurrent + currentToFringe;
// Determine the distance to the current vertexIndex
int shortPathDistance = shortestPaths.get(vertexIndex).getDistance();
// Compare the distance through currentVertex with the current distance in the vertex with index vertexIndex
if (startToFringe < shortPathDistance) { // If it is smaller, then the vertex at vertexIndex is assigned the new shortest path
List newParents = new ArrayList<>(shortestPaths.get(currentVertex).getParentVertices()); // Create a copy of the list of vertices of vertex currentVert's parents
newParents.add(currentVertex); // And add currentVertex to it as the previous vertex
shortestPaths.get(vertexIndex).setParentVertices(newParents); // Save the new path
shortestPaths.get(vertexIndex).setDistance(startToFringe); // Save the new distance
}
vertexIndex++;
}
}
private void displayPaths() { // A method for displaying the shortest paths on the screen
for (int i = 0; i < numberOfVertices; i++) {
System.out.print(vertexList[i].getLabel() + " = ");
if (shortestPaths.get(i).getDistance() == INFINITY) {
System.out.println("0");
} else {
String result = shortestPaths.get(i).getDistance() + " (";
List parents = shortestPaths.get(i).getParentVertices();
for (int j = 0; j < parents.size(); j++) {
result += vertexList[parents.get(j)].getLabel() + " -> ";
}
System.out.println(result + vertexList[i].getLabel() + ")");
}
}
}
}public class Solution {
public static void main(String[] args) {
Graph graph = new Graph();
graph.addVertex('A');
graph.addVertex('B');
graph.addVertex('C');
graph.addVertex('D');
graph.addVertex('E');
graph.addVertex('F');
graph.addVertex('G');
graph.addEdge(0, 1, 3);
graph.addEdge(0, 2, 5);
graph.addEdge(0, 3, 7);
graph.addEdge(1, 4, 6);
graph.addEdge(2, 4, 4);
graph.addEdge(2, 3, 3);
graph.addEdge(3, 5, 3);
graph.addEdge(4, 6, 6);
graph.addEdge(5, 6, 4);
System.out.println("The following nodes form the shortest paths from node A:");
graph.path();
graph.clear();
}
}

