 Dzisiaj porozmawiamy o grafach i algorytmach z nimi związanych. Wykres jest jedną z najbardziej elastycznych i wszechstronnych struktur w programowaniu. Wykres G definiuje się zazwyczaj za pomocą pary zbiorów, tj. G = (V, R), gdzie:
Dzisiaj porozmawiamy o grafach i algorytmach z nimi związanych. Wykres jest jedną z najbardziej elastycznych i wszechstronnych struktur w programowaniu. Wykres G definiuje się zazwyczaj za pomocą pary zbiorów, tj. G = (V, R), gdzie:
- V jest zbiorem wierzchołków;
- R jest zbiorem linii łączących pary wierzchołków.
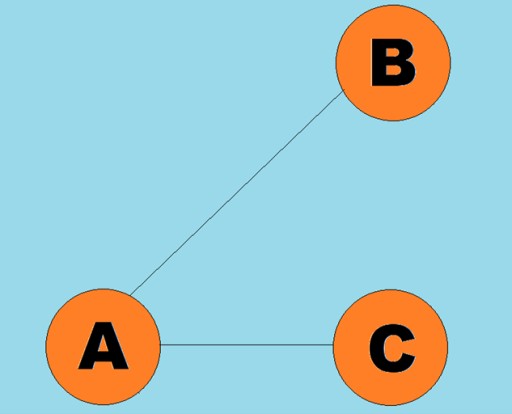 Linie skierowane nazywane są łukami:
Linie skierowane nazywane są łukami: 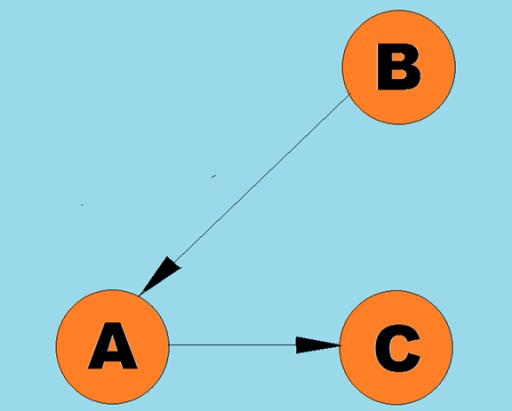 Zazwyczaj wykres jest reprezentowany przez diagram, na którym niektóre wierzchołki są połączone krawędziami (łukami). Wykresy, których krawędzie wskazują kierunek przechodzenia, nazywane są wykresami skierowanymi. Jeśli graf jest połączony krawędziami, które nie wskazują kierunku przechodzenia, to mówimy, że jest to graf nieskierowany. Oznacza to, że możliwy jest ruch w obu kierunkach: zarówno z wierzchołka A do wierzchołka B, jak i z wierzchołka B do wierzchołka A. Graf spójny to graf, w którym co najmniej jedna droga prowadzi z każdego wierzchołka do dowolnego innego wierzchołka (jak w przypadku przykład powyżej). Jeśli tak nie jest, mówimy, że graf jest rozłączony:
Zazwyczaj wykres jest reprezentowany przez diagram, na którym niektóre wierzchołki są połączone krawędziami (łukami). Wykresy, których krawędzie wskazują kierunek przechodzenia, nazywane są wykresami skierowanymi. Jeśli graf jest połączony krawędziami, które nie wskazują kierunku przechodzenia, to mówimy, że jest to graf nieskierowany. Oznacza to, że możliwy jest ruch w obu kierunkach: zarówno z wierzchołka A do wierzchołka B, jak i z wierzchołka B do wierzchołka A. Graf spójny to graf, w którym co najmniej jedna droga prowadzi z każdego wierzchołka do dowolnego innego wierzchołka (jak w przypadku przykład powyżej). Jeśli tak nie jest, mówimy, że graf jest rozłączony: 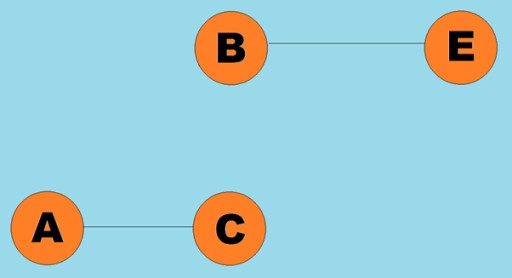 wagi można przypisać także krawędziom (łukom). Wagi to liczby, które reprezentują na przykład fizyczną odległość między dwoma wierzchołkami (lub względny czas podróży między dwoma wierzchołkami). Te wykresy nazywane są wykresami ważonymi:
wagi można przypisać także krawędziom (łukom). Wagi to liczby, które reprezentują na przykład fizyczną odległość między dwoma wierzchołkami (lub względny czas podróży między dwoma wierzchołkami). Te wykresy nazywane są wykresami ważonymi: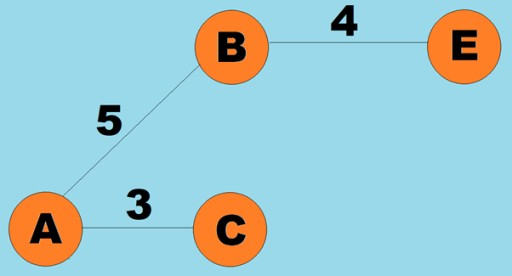
3. Algorytmy odnajdywania ścieżki (najpierw w głąb, najpierw wszerz)
Jedną z podstawowych operacji wykonywanych na grafach jest określenie wszystkich wierzchołków osiągalnych z danego wierzchołka. Wyobraź sobie, że próbujesz ustalić, w jaki sposób możesz dojechać autobusem z jednego miasta do drugiego, uwzględniając możliwe przesiadki. Do niektórych miast można dotrzeć bezpośrednio, do innych można dotrzeć jedynie przejazdem przez inne miasta. Istnieje wiele innych sytuacji, w których może być konieczne znalezienie wszystkich wierzchołków, do których można dotrzeć z danego wierzchołka. Istnieją dwa główne sposoby przeglądania grafów: najpierw w głąb i wszerz. Przeanalizujemy oba te elementy. Obie metody przechodzą przez wszystkie połączone wierzchołki. Aby dokładniej zbadać algorytmy najpierw w głąb i wszerz, użyjemy następującego wykresu:
Przeszukiwanie najpierw w głąb
Jest to jedna z najpopularniejszych metod przechodzenia przez graf. Strategia „najgłębsza” polega na wejściu w wykres tak głęboko, jak to możliwe. Następnie po dotarciu do ślepego zaułka wracamy do najbliższego wierzchołka, który nie odwiedził wcześniej sąsiednich wierzchołków. Algorytm ten przechowuje informacje na stosie o tym, dokąd wrócić, gdy dotrze się do ślepego zaułka. Zasady wyszukiwania w głąb:- Odwiedź wcześniej nieodwiedzony sąsiedni wierzchołek, oznacz go jako odwiedzony i włóż na stos.
- Przejdź do tego wierzchołka.
- Powtórz krok 1.
- Jeśli krok 1 jest niemożliwy, wróć do poprzedniego wierzchołka i spróbuj wykonać krok 1. Jeśli nie jest to możliwe, wróć do wierzchołka poprzedzającego, i tak dalej, aż znajdziemy wierzchołek, z którego będziemy mogli kontynuować przechodzenie.
- Kontynuuj, aż wszystkie wierzchołki znajdą się na stosie.
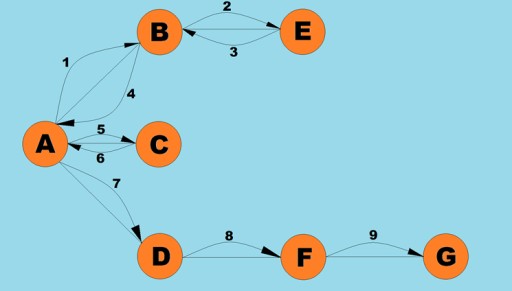 Przyjrzyjmy się, jak mógłby wyglądać kod Java dla tego algorytmu:
Przyjrzyjmy się, jak mógłby wyglądać kod Java dla tego algorytmu:
public class Graph {
private final int MAX_VERTS = 10;
private Vertex vertexArray[]; // Array of vertices
private int adjMat[][]; // Adjacency matrix
private int nVerts; // Current number of vertices
private Stack stack;
public Graph() { // Initialize internal fields
vertexArray = new Vertex[MAX_VERTS];
adjMat = new int[MAX_VERTS][MAX_VERTS];
nVerts = 0;
for (int j = 0; j < MAX_VERTS; j++) {
for (int k = 0; k < MAX_VERTS; k++) {
adjMat[j][k] = 0;
}
}
stack = new Stack<>();
}
public void addVertex(char lab) {
vertexArray[nVerts++] = new Vertex(lab);
}
public void addEdge(int start, int end) {
adjMat[start][end] = 1;
adjMat[end][start] = 1;
}
public void displayVertex(int v) {
System.out.println(vertexArray[v].getLabel());
}
public void dfs() { // Depth-first search
vertexArray[0].setVisited(true); // Take the first vertex
displayVertex(0);
stack.push(0);
while (!stack.empty()) {
int v = getAdjUnvisitedVertex(stack.peek()); // Return the index of the adjacent vertex: if any, 1; if not, -1
if (v == -1) { // If there is no unvisited adjacent vertex
stack.pop(); // The element is removed from the stack
}
else {
vertexArray[v].setVisited(true);
displayVertex(v);
stack.push(v); // The element goes on top of the stack
}
}
for (int j = 0; j < nVerts; j++) { // Reset the flags
vertexArray[j].visited = false;
}
}
private int getAdjUnvisitedVertex(int v) {
for (int j = 0; j < nVerts; j++) {
if (adjMat[v][j] == 1 && vertexArray[j].visited == false) {
return j; // Returns the first vertex found
}
}
return -1;
}
}public class Vertex {
private char label; // for example, 'A'
public boolean visited;
public Vertex(final char label) {
this.label = label;
visited = false;
}
public char getLabel() {
return this.label;
}
public boolean isVisited() {
return this.visited;
}
public void setVisited(final boolean visited) {
this.visited = visited;
}
}public class Solution {
public static void main(String[] args) {
Graph graph = new Graph();
graph.addVertex('A'); //0
graph.addVertex('B'); //1
graph.addVertex('C'); //2
graph.addVertex('D'); //3
graph.addVertex('E'); //4
graph.addVertex('F'); //5
graph.addVertex('G'); //6
graph.addEdge(0,1);
graph.addEdge(0,2);
graph.addEdge(0,3);
graph.addEdge(1,4);
graph.addEdge(3,5);
graph.addEdge(5,6);
System.out.println("Visits: ");
graph.dfs();
}
}Wyszukiwanie wszerz
Podobnie jak przeszukiwanie w głąb, algorytm ten jest jedną z najprostszych i najbardziej podstawowych metod przechodzenia przez graf. Istotą jest to, że mamy pewien bieżący wierzchołek. Umieszczamy wszystkie jego nieodwiedzone sąsiednie wierzchołki w kolejce i wybieramy kolejny element (który jest wierzchołkiem przechowywanym na początku kolejki), który staje się bieżącym wierzchołkiem… Dzieląc ten algorytm na etapy, możemy wyróżnić następujące kroki:- Odwiedź kolejny wcześniej nieodwiedzony wierzchołek sąsiadujący z bieżącym wierzchołkiem, oznacz go jako odwiedzony wcześniej i dodaj do kolejki.
- Jeśli nie można wykonać kroku nr 1, usuń wierzchołek z kolejki i ustaw go jako wierzchołek bieżący.
- Jeśli nie można wykonać kroków #1 i #2, to kończymy przechodzenie — każdy wierzchołek został przebyty (jeśli mamy spójny graf).
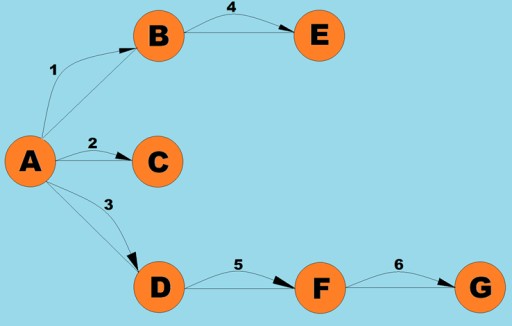 Klasa graph jest tutaj prawie identyczna z tą, której użyliśmy w algorytmie przeszukiwania w głąb, z wyjątkiem samej metody wyszukiwania i faktu, że kolejka zastępuje wewnętrzny stos:
Klasa graph jest tutaj prawie identyczna z tą, której użyliśmy w algorytmie przeszukiwania w głąb, z wyjątkiem samej metody wyszukiwania i faktu, że kolejka zastępuje wewnętrzny stos:
public class Graph {
private final int MAX_VERTS = 10;
private Vertex vertexList[]; // Array of vertices
private int adjMat[][]; // Adjacency matrix
private int nVerts; // Current number of vertices
private Queue queue;
public Graph() {
vertexList = new Vertex[MAX_VERTS];
adjMat = new int[MAX_VERTS][MAX_VERTS];
nVerts = 0;
for (int j = 0; j < MAX_VERTS; j++) {
for (int k = 0; k < MAX_VERTS; k++) { // Fill the adjacency matrix with zeros
adjMat[j][k] = 0;
}
}
queue = new PriorityQueue<>();
}
public void addVertex(char lab) {
vertexList[nVerts++] = new Vertex(lab);
}
public void addEdge(int start, int end) {
adjMat[start][end] = 1;
adjMat[end][start] = 1;
}
public void displayVertex(int v) {
System.out.println(vertexList[v].getLabel());
}
public void bfc() { // Depth-first search
vertexList[0].setVisited(true);
displayVertex(0);
queue.add(0);
int v2;
while (!queue.isEmpty()) {
int v = queue.remove();
while((v2 = getAdjUnvisitedVertex(v))!=-1) {// The loop runs until every adjacent vertex is found and added to the queue
vertexList[v2].visited = true;
displayVertex(v2);
queue.add(v2);
}
}
for (int j = 0; j < nVerts; j++) { // Reset the flags
vertexList[j].visited = false;
}
}
private int getAdjUnvisitedVertex(int v) {
for (int j = 0; j < nVerts; j++) {
if (adjMat[v][j] == 1 && vertexList[j].visited == false) {
return j; // Returns the first vertext found
}
}
return -1;
}
}public class Solution {
public static void main(String[] args) {
Graph graph = new Graph();
graph.addVertex('A'); //0
graph.addVertex('B'); //1
graph.addVertex('C'); //2
graph.addVertex('D'); //3
graph.addVertex('E'); //4
graph.addVertex('F'); //5
graph.addVertex('G'); //6
graph.addEdge(0,1);
graph.addEdge(0,2);
graph.addEdge(0,3);
graph.addEdge(1,4);
graph.addEdge(3,5);
graph.addEdge(5,6);
System.out.println("Visits: ");
graph.bfc();
}
}4. Algorytm Dijkstry
Jak wspomniano wcześniej, grafy mogą być skierowane lub nieskierowane. I pamiętasz, że można je również ważyć. Ważone grafy skierowane modelują zależności często spotykane w prawdziwym życiu: na przykład mapa miast, w której miasta są wierzchołkami, a krawędzie pomiędzy nimi to drogi o ruchu jednokierunkowym, płynącym w kierunku skierowanej krawędzi. Załóżmy, że jesteś firmą transportową i chcesz znaleźć najkrótszą trasę pomiędzy dwoma odległymi miastami. Jak byś to zrobił? Znalezienie najkrótszej ścieżki pomiędzy dwoma wierzchołkami jest jednym z najczęstszych problemów rozwiązywanych za pomocą grafów ważonych. Aby rozwiązać ten problem, używamy algorytmu Dijkstry. Po uruchomieniu będziesz znać najkrótsze ścieżki z danego początkowego wierzchołka do każdego innego. Jakie są kroki tego algorytmu? Spróbuję odpowiedzieć na to pytanie. Kroki algorytmu Dijkstry:- Krok 1: Znajdź sąsiedni węzeł, który ma najniższy koszt nawigacji (najniższa waga krawędzi). Stoisz na samym początku i zastanawiasz się, dokąd pójść: do węzła A czy węzła B. Jaki jest koszt przejścia do każdego z tych węzłów?
- Krok 2: oblicz odległość, jaką należy pokonać do wszystkich sąsiadów węzła В, których algorytm nie odwiedził jeszcze podczas przechodzenia przez krawędź z В. Jeżeli nowa odległość jest mniejsza od starej, wówczas ścieżka przechodząca przez krawędź B staje się nową najkrótszą ścieżką dla tego wierzchołka.
- Krok 3: Oznacz wierzchołek B jako odwiedzony.
- Krok 4: Przejdź do kroku 1.
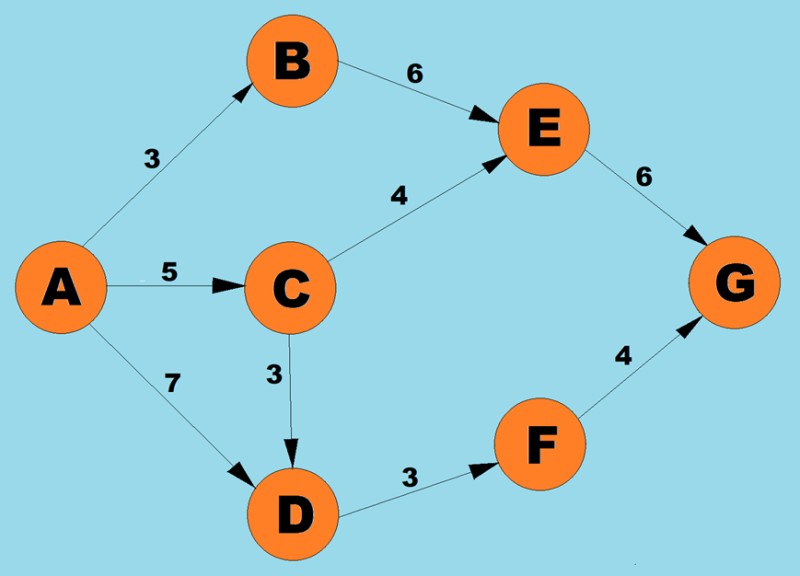 Korzystając z powyższego algorytmu, wyznaczymy najkrótszą ścieżkę od A do G:
Korzystając z powyższego algorytmu, wyznaczymy najkrótszą ścieżkę od A do G:
- Dla wierzchołka A możliwe są trzy ścieżki: do B o wadze 3, do С o wadze 5 i do D o wadze 7. Zgodnie z pierwszym krokiem algorytmu wybieramy węzeł o najniższym koszcie (waga krawędzi). W tym przypadku B.
-
Ponieważ jedynym nieodwiedzonym sąsiadem B jest wierzchołek Е, sprawdzamy, jaka byłaby ścieżka, gdybyśmy przeszli przez ten wierzchołek. 3(AB) + 6(BE) = 9.
Zatem rejestrujemy, że najkrótsza obecnie ścieżka od A do E wynosi 9.
-
Ponieważ nasza praca z wierzchołkiem B została zakończona, przystępujemy do wybierania kolejnego wierzchołka, którego krawędź ma minimalną wagę.
Z wierzchołków A i B możliwościami są wierzchołki D (7), C (5) lub E (6).
Krawędź do С ma najmniejszą wagę, więc przechodzimy do tego wierzchołka.
-
Następnie, tak jak poprzednio, przechodząc przez C, znajdujemy najkrótszą ścieżkę do sąsiednich wierzchołków:
-
AD = 5 (AC) + 3 (CD) = 8, ale ponieważ poprzednia najkrótsza ścieżka (AC = 7) jest krótsza niż ta przechodząca przez С, najkrótszą ścieżkę (AC = 7) pozostawiamy bez zmian.
-
CE = 5(AC) + 4(CE) = 9. Ta nowa najkrótsza ścieżka jest równa poprzedniej, więc ją również pozostawiamy bez zmian.
-
-
Z najbliższych dostępnych wierzchołków (E i D) wybierz wierzchołek o najmniejszej wadze krawędzi, czyli D (3).
-
Znajdujemy najkrótszą ścieżkę do sąsiada F.
AF = 7(AD) + 3(DF) = 9
-
Z najbliższych dostępnych wierzchołków (E i F) wybierz wierzchołek o najmniejszej wadze krawędzi, czyli F (3).
-
Znajdź najkrótszą drogę do sąsiada G.
AG = 7(AD) + 3(DF) + 4(FG) = 14
Znaleźliśmy więc ścieżkę od A do G.
Ale żeby mieć pewność, że będzie najkrótszy, musimy także wykonać nasze kroki na wierzchołku E.
-
Ponieważ wierzchołek G nie ma sąsiadujących wierzchołków wskazanych przez skierowane krawędzie, pozostał nam tylko wierzchołek E, więc go wybieramy.
-
Znajdź najkrótszą ścieżkę do sąsiada G.
AG = 3 (AB) + 6 (BE) + 6 (EG) = 15. Ta ścieżka jest dłuższa niż poprzednia najkrótsza ścieżka (AG (14)), więc pozostawiamy tę ścieżkę bez zmian.
Ponieważ z G nie prowadzą żadne wierzchołki, nie ma sensu wykonywać kroków algorytmu na tym wierzchołku. Oznacza to, że praca algorytmu została zakończona.
public class Vertex {
private char label;
private boolean isInTree;
public Vertex(char label) {
this.label = label;
this.isInTree = false;
}
public char getLabel() {
return label;
}
public void setLabel(char label) {
this.label = label;
}
public boolean isInTree() {
return isInTree;
}
public void setInTree(boolean inTree) {
isInTree = inTree;
}
}public class Path { // A class that contains the distance and the previous and traversed vertices
private int distance; // Current distance from the starting vertex
private List parentVertices; // Current parent vertex
public Path(int distance) {
this.distance = distance;
this.parentVertices = new ArrayList<>();
}
public int getDistance() {
return distance;
}
public void setDistance(int distance) {
this.distance = distance;
}
public List getParentVertices() {
return parentVertices;
}
public void setParentVertices(List parentVertices) {
this.parentVertices = parentVertices;
}
}public class Graph {
private final int MAX_VERTS = 10;// Maximum number of vertices
private final int INFINITY = 100000000; // This number represents infinity
private Vertex vertexList[]; // List of vertices
private int relationMatrix[][]; // Matrix of edges between vertices
private int numberOfVertices; // Current number of vertices
private int numberOfVerticesInTree; // Number of visited vertices in the tree
private List shortestPaths; // List of shortest paths
private int currentVertex; // Current vertex
private int startToCurrent; // Distance to currentVertex
public Graph() {
vertexList = new Vertex[MAX_VERTS]; // Adjacency matrix
relationMatrix = new int[MAX_VERTS][MAX_VERTS];
numberOfVertices = 0;
numberOfVerticesInTree = 0;
for (int i = 0; i < MAX_VERTS; i++) { // Fill the adjacency matrix
for (int k = 0; k < MAX_VERTS; k++) { // with "infinity"
relationMatrix[i][k] = INFINITY; // Assign default values
shortestPaths = new ArrayList<>(); // Assign an empty list
}
}
}
public void addVertex(char lab) {// Assign new vertices
vertexList[numberOfVertices++] = new Vertex(lab);
}
public void addEdge(int start, int end, int weight) {
relationMatrix[start][end] = weight; // Set weighted edges between vertices
}
public void path() { // Choose the shortest path
// Set the initial vertex data
int startTree = 0; // Start from vertex 0
vertexList[startTree].setInTree(true); // Include the first element in the tree
numberOfVerticesInTree = 1;
// Fill out the shortest paths for vertices adjacent to the initial vertex
for (int i = 0; i < numberOfVertices; i++) {
int tempDist = relationMatrix[startTree][i];
Path path = new Path(tempDist);
path.getParentVertices().add(0);// The starting vertex will always be a parent vertex
shortestPaths.add(path);
}
// Until every vertex is in the tree
while (numberOfVerticesInTree < numberOfVertices) { // Do this until the number of of vertices in the tree equals the total number of vertices
int indexMin = getMin();// Get the index of the of the vertex with the smallest distance from the vertices not yet in the tree
int minDist = shortestPaths.get(indexMin).getDistance(); // Minimum distance to the vertices not yet in the tree
if (minDist == INFINITY) {
System.out.println("The graph has an unreachable vertex");
break; // If only unreachable vertices have not been visited, then we exit the loop
} else {
currentVertex = indexMin; // Set currentVert to the index of the current vertex
startToCurrent = shortestPaths.get(indexMin).getDistance(); // Set the distance to the current vertex
}
vertexList[currentVertex].setInTree(true); // Add the current vertex to the tree
numberOfVerticesInTree++; // Increase the count of vertices in the tree
updateShortestPaths(); // Update the list of shortest paths
}
displayPaths(); // Display the results on the console
}
public void clear() { // Clear the tree
numberOfVerticesInTree = 0;
for (int i = 0; i < numberOfVertices; i++) {
vertexList[i].setInTree(false);
}
}
private int getMin() {
int minDist = INFINITY; // The distance of the initial shortest path is taken to be infinite
int indexMin = 0;
for (int i = 1; i < numberOfVertices; i++) { // For each vertex
if (!vertexList[i].isInTree() && shortestPaths.get(i).getDistance() < minDist) { // If the vertex is not yet in the tree and the distance to the vertex is less than the current minimum
minDist = shortestPaths.get(i).getDistance(); // then update the minimum
indexMin = i; // Update the index of the vertex with the minimum distance
}
}
return indexMin; // Returns the index of the vertex with the smallest distance among those not yet in the tree
}
private void updateShortestPaths() {
int vertexIndex = 1; // The initial vertex is skipped
while (vertexIndex < numberOfVertices) { // Run over the columns
if (vertexList[vertexIndex].isInTree()) { // If the column vertex is already in the tree, then we skip it
vertexIndex++;
continue;
}
// Calculate the distance for one element sPath
// Get the edge from currentVert to column
int currentToFringe = relationMatrix[currentVertex][vertexIndex];
// Add up all the distances
int startToFringe = startToCurrent + currentToFringe;
// Determine the distance to the current vertexIndex
int shortPathDistance = shortestPaths.get(vertexIndex).getDistance();
// Compare the distance through currentVertex with the current distance in the vertex with index vertexIndex
if (startToFringe < shortPathDistance) { // If it is smaller, then the vertex at vertexIndex is assigned the new shortest path
List newParents = new ArrayList<>(shortestPaths.get(currentVertex).getParentVertices()); // Create a copy of the list of vertices of vertex currentVert's parents
newParents.add(currentVertex); // And add currentVertex to it as the previous vertex
shortestPaths.get(vertexIndex).setParentVertices(newParents); // Save the new path
shortestPaths.get(vertexIndex).setDistance(startToFringe); // Save the new distance
}
vertexIndex++;
}
}
private void displayPaths() { // A method for displaying the shortest paths on the screen
for (int i = 0; i < numberOfVertices; i++) {
System.out.print(vertexList[i].getLabel() + " = ");
if (shortestPaths.get(i).getDistance() == INFINITY) {
System.out.println("0");
} else {
String result = shortestPaths.get(i).getDistance() + " (";
List parents = shortestPaths.get(i).getParentVertices();
for (int j = 0; j < parents.size(); j++) {
result += vertexList[parents.get(j)].getLabel() + " -> ";
}
System.out.println(result + vertexList[i].getLabel() + ")");
}
}
}
}public class Solution {
public static void main(String[] args) {
Graph graph = new Graph();
graph.addVertex('A');
graph.addVertex('B');
graph.addVertex('C');
graph.addVertex('D');
graph.addVertex('E');
graph.addVertex('F');
graph.addVertex('G');
graph.addEdge(0, 1, 3);
graph.addEdge(0, 2, 5);
graph.addEdge(0, 3, 7);
graph.addEdge(1, 4, 6);
graph.addEdge(2, 4, 4);
graph.addEdge(2, 3, 3);
graph.addEdge(3, 5, 3);
graph.addEdge(4, 6, 6);
graph.addEdge(5, 6, 4);
System.out.println("The following nodes form the shortest paths from node A:");
graph.path();
graph.clear();
}
}

