 Heute werden wir über Diagramme und die damit verbundenen Algorithmen sprechen. Ein Graph ist eine der flexibelsten und vielseitigsten Strukturen in der Programmierung. Der Graph G wird normalerweise durch ein Mengenpaar definiert, d. h. G = (V, R), wobei:
Heute werden wir über Diagramme und die damit verbundenen Algorithmen sprechen. Ein Graph ist eine der flexibelsten und vielseitigsten Strukturen in der Programmierung. Der Graph G wird normalerweise durch ein Mengenpaar definiert, d. h. G = (V, R), wobei:
- V ist eine Menge von Eckpunkten;
- R ist eine Menge von Linien, die Scheitelpunktpaare verbinden.
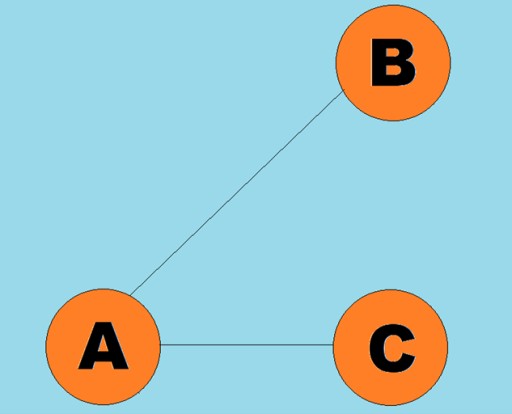 Gerichtete Linien heißen Bögen:
Gerichtete Linien heißen Bögen: 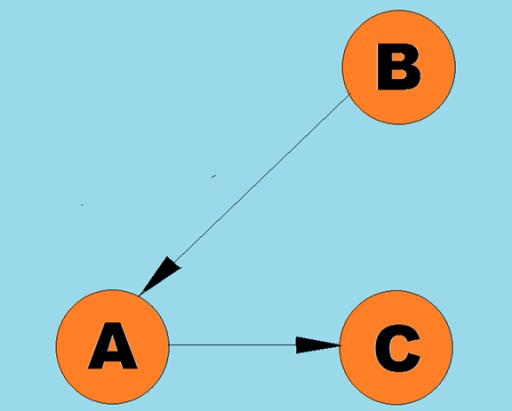 Typischerweise wird ein Graph durch ein Diagramm dargestellt, in dem einige der Eckpunkte durch Kanten (Bögen) verbunden sind. Graphen, deren Kanten eine Durchlaufrichtung angeben, werden gerichtete Graphen genannt. Wenn ein Graph durch Kanten verbunden ist, die nicht die Durchlaufrichtung angeben, dann spricht man von einem ungerichteten Graphen. Dies bedeutet, dass eine Bewegung in beide Richtungen möglich ist: sowohl von Scheitelpunkt A zu Scheitelpunkt B als auch von Scheitelpunkt B zu Scheitelpunkt A. Ein verbundener Graph ist ein Graph, in dem mindestens ein Pfad von jedem Scheitelpunkt zu jedem anderen Scheitelpunkt führt (wie im Beispiel oben). Ist dies nicht der Fall, spricht man von einem unzusammenhängenden Graphen:
Typischerweise wird ein Graph durch ein Diagramm dargestellt, in dem einige der Eckpunkte durch Kanten (Bögen) verbunden sind. Graphen, deren Kanten eine Durchlaufrichtung angeben, werden gerichtete Graphen genannt. Wenn ein Graph durch Kanten verbunden ist, die nicht die Durchlaufrichtung angeben, dann spricht man von einem ungerichteten Graphen. Dies bedeutet, dass eine Bewegung in beide Richtungen möglich ist: sowohl von Scheitelpunkt A zu Scheitelpunkt B als auch von Scheitelpunkt B zu Scheitelpunkt A. Ein verbundener Graph ist ein Graph, in dem mindestens ein Pfad von jedem Scheitelpunkt zu jedem anderen Scheitelpunkt führt (wie im Beispiel oben). Ist dies nicht der Fall, spricht man von einem unzusammenhängenden Graphen:  Den Kanten (Bögen) können auch Gewichte zugewiesen werden. Die Gewichte sind Zahlen, die beispielsweise den physischen Abstand zwischen zwei Eckpunkten (oder die relative Reisezeit zwischen zwei Eckpunkten) darstellen. Diese Diagramme werden gewichtete Diagramme genannt:
Den Kanten (Bögen) können auch Gewichte zugewiesen werden. Die Gewichte sind Zahlen, die beispielsweise den physischen Abstand zwischen zwei Eckpunkten (oder die relative Reisezeit zwischen zwei Eckpunkten) darstellen. Diese Diagramme werden gewichtete Diagramme genannt: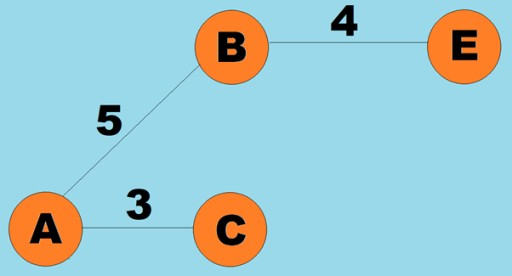
3. Pathfinding-Algorithmen (Tiefe zuerst, Breite zuerst)
Eine der Grundoperationen, die mit Graphen durchgeführt werden, ist die Bestimmung aller von einem gegebenen Scheitelpunkt aus erreichbaren Scheitelpunkte. Stellen Sie sich vor, Sie versuchen herauszufinden, wie Sie mit dem Bus von einer Stadt in eine andere fahren können, einschließlich möglicher Transfers. Einige Städte können direkt erreicht werden, während andere nur über andere Städte erreichbar sind. Es gibt viele andere Situationen, in denen Sie möglicherweise alle Scheitelpunkte finden müssen, die Sie von einem bestimmten Scheitelpunkt aus erreichen können. Es gibt zwei Hauptmethoden zum Durchlaufen von Diagrammen: zuerst mit der Tiefe und zuerst mit der Breite. Wir werden beides untersuchen. Beide Methoden durchlaufen alle verbundenen Scheitelpunkte. Um die Tiefen- und Breitenalgorithmen weiter zu untersuchen, verwenden wir das folgende Diagramm:
Tiefensuche
Dies ist eine der gebräuchlichsten Methoden zum Durchlaufen von Graphen. Die Tiefenstrategie besteht darin, so tief wie möglich in ein Diagramm einzudringen. Nachdem wir eine Sackgasse erreicht haben, kehren wir zum nächstgelegenen Scheitelpunkt zurück, der zuvor nicht besuchte benachbarte Scheitelpunkte hatte. Dieser Algorithmus speichert auf dem Stapel Informationen darüber, wohin er zurückkehren soll, wenn eine Sackgasse erreicht wird. Regeln für die Tiefensuche:- Besuchen Sie einen zuvor nicht besuchten benachbarten Scheitelpunkt, markieren Sie ihn als besucht und schieben Sie ihn auf den Stapel.
- Gehen Sie zu diesem Scheitelpunkt.
- Wiederholen Sie Schritt 1.
- Wenn Schritt 1 nicht möglich ist, kehren Sie zum vorherigen Scheitelpunkt zurück und versuchen Sie, Schritt 1 auszuführen. Wenn dies nicht möglich ist, kehren Sie zum Scheitelpunkt davor zurück und so weiter, bis wir einen Scheitelpunkt finden, von dem aus wir die Durchquerung fortsetzen können.
- Fahren Sie fort, bis alle Scheitelpunkte auf dem Stapel liegen.
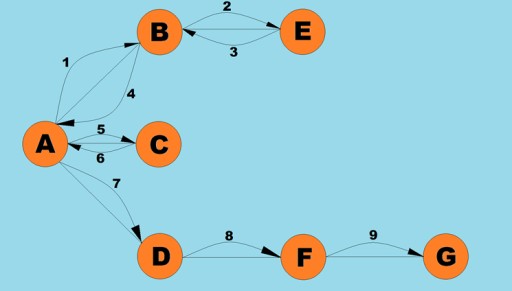 Schauen wir uns an, wie der Java-Code für diesen Algorithmus aussehen könnte:
Schauen wir uns an, wie der Java-Code für diesen Algorithmus aussehen könnte:
public class Graph {
private final int MAX_VERTS = 10;
private Vertex vertexArray[]; // Array of vertices
private int adjMat[][]; // Adjacency matrix
private int nVerts; // Current number of vertices
private Stack stack;
public Graph() { // Initialize internal fields
vertexArray = new Vertex[MAX_VERTS];
adjMat = new int[MAX_VERTS][MAX_VERTS];
nVerts = 0;
for (int j = 0; j < MAX_VERTS; j++) {
for (int k = 0; k < MAX_VERTS; k++) {
adjMat[j][k] = 0;
}
}
stack = new Stack<>();
}
public void addVertex(char lab) {
vertexArray[nVerts++] = new Vertex(lab);
}
public void addEdge(int start, int end) {
adjMat[start][end] = 1;
adjMat[end][start] = 1;
}
public void displayVertex(int v) {
System.out.println(vertexArray[v].getLabel());
}
public void dfs() { // Depth-first search
vertexArray[0].setVisited(true); // Take the first vertex
displayVertex(0);
stack.push(0);
while (!stack.empty()) {
int v = getAdjUnvisitedVertex(stack.peek()); // Return the index of the adjacent vertex: if any, 1; if not, -1
if (v == -1) { // If there is no unvisited adjacent vertex
stack.pop(); // The element is removed from the stack
}
else {
vertexArray[v].setVisited(true);
displayVertex(v);
stack.push(v); // The element goes on top of the stack
}
}
for (int j = 0; j < nVerts; j++) { // Reset the flags
vertexArray[j].visited = false;
}
}
private int getAdjUnvisitedVertex(int v) {
for (int j = 0; j < nVerts; j++) {
if (adjMat[v][j] == 1 && vertexArray[j].visited == false) {
return j; // Returns the first vertex found
}
}
return -1;
}
}public class Vertex {
private char label; // for example, 'A'
public boolean visited;
public Vertex(final char label) {
this.label = label;
visited = false;
}
public char getLabel() {
return this.label;
}
public boolean isVisited() {
return this.visited;
}
public void setVisited(final boolean visited) {
this.visited = visited;
}
}public class Solution {
public static void main(String[] args) {
Graph graph = new Graph();
graph.addVertex('A'); //0
graph.addVertex('B'); //1
graph.addVertex('C'); //2
graph.addVertex('D'); //3
graph.addVertex('E'); //4
graph.addVertex('F'); //5
graph.addVertex('G'); //6
graph.addEdge(0,1);
graph.addEdge(0,2);
graph.addEdge(0,3);
graph.addEdge(1,4);
graph.addEdge(3,5);
graph.addEdge(5,6);
System.out.println("Visits: ");
graph.dfs();
}
}Breitensuche
Dieser Algorithmus ist wie die Tiefensuche eine der einfachsten und grundlegendsten Methoden zum Durchlaufen von Graphen. Das Wesentliche ist, dass wir einen aktuellen Scheitelpunkt haben. Wir stellen alle nicht besuchten benachbarten Scheitelpunkte in eine Warteschlange und wählen das nächste Element aus (das ist der Scheitelpunkt, der am Anfang der Warteschlange gespeichert ist), das zum aktuellen Scheitelpunkt wird. Wenn wir diesen Algorithmus in Phasen aufteilen, können wir die folgenden Schritte identifizieren:- Besuchen Sie den nächsten zuvor nicht besuchten Scheitelpunkt neben dem aktuellen Scheitelpunkt, markieren Sie ihn im Voraus als besucht und fügen Sie ihn der Warteschlange hinzu.
- Wenn Schritt 1 nicht ausgeführt werden kann, entfernen Sie den Scheitelpunkt aus der Warteschlange und machen Sie ihn zum aktuellen Scheitelpunkt.
- Wenn die Schritte Nr. 1 und Nr. 2 nicht ausgeführt werden können, sind wir mit dem Durchqueren fertig – jeder Scheitelpunkt wurde durchquert (wenn wir einen verbundenen Graphen haben).
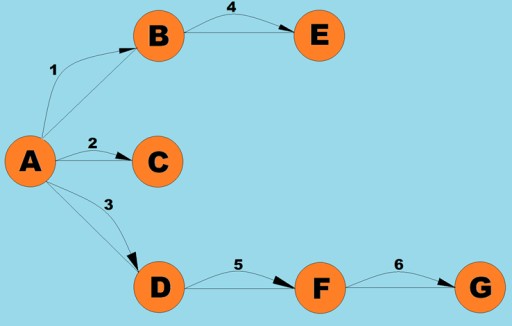 Die Graphklasse hier ist fast identisch mit der, die wir für den Tiefensuchalgorithmus verwendet haben, mit Ausnahme der Suchmethode selbst und der Tatsache, dass eine Warteschlange den internen Stapel ersetzt:
Die Graphklasse hier ist fast identisch mit der, die wir für den Tiefensuchalgorithmus verwendet haben, mit Ausnahme der Suchmethode selbst und der Tatsache, dass eine Warteschlange den internen Stapel ersetzt:
public class Graph {
private final int MAX_VERTS = 10;
private Vertex vertexList[]; // Array of vertices
private int adjMat[][]; // Adjacency matrix
private int nVerts; // Current number of vertices
private Queue queue;
public Graph() {
vertexList = new Vertex[MAX_VERTS];
adjMat = new int[MAX_VERTS][MAX_VERTS];
nVerts = 0;
for (int j = 0; j < MAX_VERTS; j++) {
for (int k = 0; k < MAX_VERTS; k++) { // Fill the adjacency matrix with zeros
adjMat[j][k] = 0;
}
}
queue = new PriorityQueue<>();
}
public void addVertex(char lab) {
vertexList[nVerts++] = new Vertex(lab);
}
public void addEdge(int start, int end) {
adjMat[start][end] = 1;
adjMat[end][start] = 1;
}
public void displayVertex(int v) {
System.out.println(vertexList[v].getLabel());
}
public void bfc() { // Depth-first search
vertexList[0].setVisited(true);
displayVertex(0);
queue.add(0);
int v2;
while (!queue.isEmpty()) {
int v = queue.remove();
while((v2 = getAdjUnvisitedVertex(v))!=-1) {// The loop runs until every adjacent vertex is found and added to the queue
vertexList[v2].visited = true;
displayVertex(v2);
queue.add(v2);
}
}
for (int j = 0; j < nVerts; j++) { // Reset the flags
vertexList[j].visited = false;
}
}
private int getAdjUnvisitedVertex(int v) {
for (int j = 0; j < nVerts; j++) {
if (adjMat[v][j] == 1 && vertexList[j].visited == false) {
return j; // Returns the first vertext found
}
}
return -1;
}
}public class Solution {
public static void main(String[] args) {
Graph graph = new Graph();
graph.addVertex('A'); //0
graph.addVertex('B'); //1
graph.addVertex('C'); //2
graph.addVertex('D'); //3
graph.addVertex('E'); //4
graph.addVertex('F'); //5
graph.addVertex('G'); //6
graph.addEdge(0,1);
graph.addEdge(0,2);
graph.addEdge(0,3);
graph.addEdge(1,4);
graph.addEdge(3,5);
graph.addEdge(5,6);
System.out.println("Visits: ");
graph.bfc();
}
}4. Dijkstras Algorithmus
Wie bereits erwähnt, können Graphen gerichtet oder ungerichtet sein. Und Sie werden sich erinnern, dass sie auch gewichtet werden können. Gewichtete, gerichtete Diagramme modellieren Beziehungen, die im wirklichen Leben häufig vorkommen: zum Beispiel eine Karte von Städten, bei der Städte Eckpunkte sind und die Kanten zwischen ihnen Straßen mit Einbahnverkehr sind, der in Richtung der gerichteten Kante fließt. Nehmen wir an, Sie sind ein Frachtunternehmen und müssen die kürzeste Route zwischen zwei weit entfernten Städten finden. Wie würdest du es machen? Das Finden des kürzesten Weges zwischen zwei Eckpunkten ist eines der häufigsten Probleme, die mithilfe gewichteter Diagramme gelöst werden. Um dieses Problem zu lösen, verwenden wir den Dijkstra-Algorithmus. Sobald Sie es ausführen, kennen Sie die kürzesten Pfade von einem bestimmten Anfangsscheitelpunkt zu jedem anderen. Was sind die Schritte dieses Algorithmus? Ich werde versuchen, diese Frage zu beantworten. Schritte des Dijkstra-Algorithmus:- Schritt 1: Suchen Sie den benachbarten Knoten, zu dem die Navigation am wenigsten kostet (geringstes Kantengewicht). Sie stehen ganz am Anfang und überlegen, wohin Sie gehen sollen: zu Knoten A oder Knoten B. Wie hoch sind die Kosten für den Umzug zu jedem dieser Knoten?
- Schritt 2: Berechnen Sie die zurückzulegende Entfernung zu allen Nachbarn von Knoten B, die vom Algorithmus noch nicht besucht wurden, wenn Sie die Kante von Knoten B aus überqueren. Wenn der neue Abstand kleiner als der alte ist, wird der Weg durch Kante B zum neuen kürzesten Weg für diesen Scheitelpunkt.
- Schritt 3: Markieren Sie Scheitelpunkt B als besucht.
- Schritt 4: Gehen Sie zu Schritt 1.
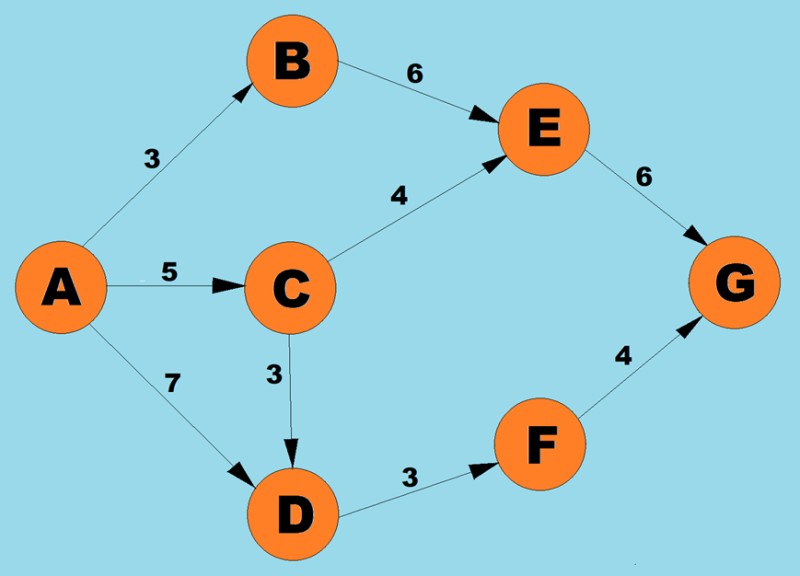 Mit dem obigen Algorithmus ermitteln wir den kürzesten Weg von A nach G:
Mit dem obigen Algorithmus ermitteln wir den kürzesten Weg von A nach G:
- Es gibt drei mögliche Pfade für Scheitelpunkt A: nach B mit Gewicht 3, nach C mit Gewicht 5 und nach D mit Gewicht 7. Gemäß dem ersten Schritt des Algorithmus wählen wir den Knoten mit den niedrigsten Kosten (Kantengewicht) aus. In diesem Fall B.
-
Da der einzige unbesuchte Nachbar von B der Scheitelpunkt Å ist, prüfen wir, wie der Pfad aussehen würde, wenn wir durch diesen Scheitelpunkt gehen würden. 3(AB) + 6(BE) = 9.
Somit zeichnen wir auf, dass der derzeit kürzeste Weg von A nach E 9 ist.
-
Da unsere Arbeit mit Scheitelpunkt B abgeschlossen ist, fahren wir mit der Auswahl des nächsten Scheitelpunkts fort, dessen Kante das minimale Gewicht hat.
Von den Eckpunkten A und B aus sind die Eckpunkte D (7), C (5) oder E (6) möglich.
Die Kante zu С hat das kleinste Gewicht, daher gehen wir zu diesem Scheitelpunkt.
-
Als nächstes finden wir wie zuvor den kürzesten Weg zu benachbarten Eckpunkten, wenn wir durch C gehen:
-
AD = 5 (AC) + 3 (CD) = 8, aber da der bisherige kürzeste Weg (AC = 7) um С kleiner als dieser ist, behalten wir den kürzesten Weg (AC = 7) unverändert bei.
-
CE = 5(AC) + 4(CE) = 9. Dieser neue kürzeste Weg ist gleich dem vorherigen, daher lassen wir ihn auch unverändert.
-
-
Wählen Sie aus den nächstgelegenen zugänglichen Scheitelpunkten (E und D) den Scheitelpunkt mit dem kleinsten Kantengewicht aus, dh D (3).
-
Wir finden den kürzesten Weg zu seinem Nachbarn F.
AF = 7(AD) + 3(DF) = 9
-
Wählen Sie aus den nächstgelegenen zugänglichen Scheitelpunkten (E und F) den Scheitelpunkt mit dem kleinsten Kantengewicht aus, dh F (3).
-
Finden Sie den kürzesten Weg zu seinem Nachbarn G.
AG = 7(AD) + 3(DF) + 4(FG) = 14
Wir haben also einen Weg von A nach G gefunden.
Aber um sicherzustellen, dass es das kürzeste ist, müssen wir unsere Schritte auch am Scheitelpunkt E ausführen.
-
Da Scheitelpunkt G keine benachbarten Scheitelpunkte hat, auf die gerichtete Kanten zeigen, bleibt nur noch Scheitelpunkt E übrig, also wählen wir ihn aus.
-
Finden Sie den kürzesten Weg zum Nachbarn G.
AG = 3 (AB) + 6 (BE) + 6 (EG) = 15. Dieser Weg ist länger als der vorherige kürzeste Weg (AG (14)), daher lassen wir diesen Weg unverändert.
Da es keine Scheitelpunkte gibt, die von G ausgehen, macht es keinen Sinn, die Schritte des Algorithmus an diesem Scheitelpunkt auszuführen. Das bedeutet, dass die Arbeit des Algorithmus abgeschlossen ist.
public class Vertex {
private char label;
private boolean isInTree;
public Vertex(char label) {
this.label = label;
this.isInTree = false;
}
public char getLabel() {
return label;
}
public void setLabel(char label) {
this.label = label;
}
public boolean isInTree() {
return isInTree;
}
public void setInTree(boolean inTree) {
isInTree = inTree;
}
}public class Path { // A class that contains the distance and the previous and traversed vertices
private int distance; // Current distance from the starting vertex
private List parentVertices; // Current parent vertex
public Path(int distance) {
this.distance = distance;
this.parentVertices = new ArrayList<>();
}
public int getDistance() {
return distance;
}
public void setDistance(int distance) {
this.distance = distance;
}
public List getParentVertices() {
return parentVertices;
}
public void setParentVertices(List parentVertices) {
this.parentVertices = parentVertices;
}
}public class Graph {
private final int MAX_VERTS = 10;// Maximum number of vertices
private final int INFINITY = 100000000; // This number represents infinity
private Vertex vertexList[]; // List of vertices
private int relationMatrix[][]; // Matrix of edges between vertices
private int numberOfVertices; // Current number of vertices
private int numberOfVerticesInTree; // Number of visited vertices in the tree
private List shortestPaths; // List of shortest paths
private int currentVertex; // Current vertex
private int startToCurrent; // Distance to currentVertex
public Graph() {
vertexList = new Vertex[MAX_VERTS]; // Adjacency matrix
relationMatrix = new int[MAX_VERTS][MAX_VERTS];
numberOfVertices = 0;
numberOfVerticesInTree = 0;
for (int i = 0; i < MAX_VERTS; i++) { // Fill the adjacency matrix
for (int k = 0; k < MAX_VERTS; k++) { // with "infinity"
relationMatrix[i][k] = INFINITY; // Assign default values
shortestPaths = new ArrayList<>(); // Assign an empty list
}
}
}
public void addVertex(char lab) {// Assign new vertices
vertexList[numberOfVertices++] = new Vertex(lab);
}
public void addEdge(int start, int end, int weight) {
relationMatrix[start][end] = weight; // Set weighted edges between vertices
}
public void path() { // Choose the shortest path
// Set the initial vertex data
int startTree = 0; // Start from vertex 0
vertexList[startTree].setInTree(true); // Include the first element in the tree
numberOfVerticesInTree = 1;
// Fill out the shortest paths for vertices adjacent to the initial vertex
for (int i = 0; i < numberOfVertices; i++) {
int tempDist = relationMatrix[startTree][i];
Path path = new Path(tempDist);
path.getParentVertices().add(0);// The starting vertex will always be a parent vertex
shortestPaths.add(path);
}
// Until every vertex is in the tree
while (numberOfVerticesInTree < numberOfVertices) { // Do this until the number of of vertices in the tree equals the total number of vertices
int indexMin = getMin();// Get the index of the of the vertex with the smallest distance from the vertices not yet in the tree
int minDist = shortestPaths.get(indexMin).getDistance(); // Minimum distance to the vertices not yet in the tree
if (minDist == INFINITY) {
System.out.println("The graph has an unreachable vertex");
break; // If only unreachable vertices have not been visited, then we exit the loop
} else {
currentVertex = indexMin; // Set currentVert to the index of the current vertex
startToCurrent = shortestPaths.get(indexMin).getDistance(); // Set the distance to the current vertex
}
vertexList[currentVertex].setInTree(true); // Add the current vertex to the tree
numberOfVerticesInTree++; // Increase the count of vertices in the tree
updateShortestPaths(); // Update the list of shortest paths
}
displayPaths(); // Display the results on the console
}
public void clear() { // Clear the tree
numberOfVerticesInTree = 0;
for (int i = 0; i < numberOfVertices; i++) {
vertexList[i].setInTree(false);
}
}
private int getMin() {
int minDist = INFINITY; // The distance of the initial shortest path is taken to be infinite
int indexMin = 0;
for (int i = 1; i < numberOfVertices; i++) { // For each vertex
if (!vertexList[i].isInTree() && shortestPaths.get(i).getDistance() < minDist) { // If the vertex is not yet in the tree and the distance to the vertex is less than the current minimum
minDist = shortestPaths.get(i).getDistance(); // then update the minimum
indexMin = i; // Update the index of the vertex with the minimum distance
}
}
return indexMin; // Returns the index of the vertex with the smallest distance among those not yet in the tree
}
private void updateShortestPaths() {
int vertexIndex = 1; // The initial vertex is skipped
while (vertexIndex < numberOfVertices) { // Run over the columns
if (vertexList[vertexIndex].isInTree()) { // If the column vertex is already in the tree, then we skip it
vertexIndex++;
continue;
}
// Calculate the distance for one element sPath
// Get the edge from currentVert to column
int currentToFringe = relationMatrix[currentVertex][vertexIndex];
// Add up all the distances
int startToFringe = startToCurrent + currentToFringe;
// Determine the distance to the current vertexIndex
int shortPathDistance = shortestPaths.get(vertexIndex).getDistance();
// Compare the distance through currentVertex with the current distance in the vertex with index vertexIndex
if (startToFringe < shortPathDistance) { // If it is smaller, then the vertex at vertexIndex is assigned the new shortest path
List newParents = new ArrayList<>(shortestPaths.get(currentVertex).getParentVertices()); // Create a copy of the list of vertices of vertex currentVert's parents
newParents.add(currentVertex); // And add currentVertex to it as the previous vertex
shortestPaths.get(vertexIndex).setParentVertices(newParents); // Save the new path
shortestPaths.get(vertexIndex).setDistance(startToFringe); // Save the new distance
}
vertexIndex++;
}
}
private void displayPaths() { // A method for displaying the shortest paths on the screen
for (int i = 0; i < numberOfVertices; i++) {
System.out.print(vertexList[i].getLabel() + " = ");
if (shortestPaths.get(i).getDistance() == INFINITY) {
System.out.println("0");
} else {
String result = shortestPaths.get(i).getDistance() + " (";
List parents = shortestPaths.get(i).getParentVertices();
for (int j = 0; j < parents.size(); j++) {
result += vertexList[parents.get(j)].getLabel() + " -> ";
}
System.out.println(result + vertexList[i].getLabel() + ")");
}
}
}
}public class Solution {
public static void main(String[] args) {
Graph graph = new Graph();
graph.addVertex('A');
graph.addVertex('B');
graph.addVertex('C');
graph.addVertex('D');
graph.addVertex('E');
graph.addVertex('F');
graph.addVertex('G');
graph.addEdge(0, 1, 3);
graph.addEdge(0, 2, 5);
graph.addEdge(0, 3, 7);
graph.addEdge(1, 4, 6);
graph.addEdge(2, 4, 4);
graph.addEdge(2, 3, 3);
graph.addEdge(3, 5, 3);
graph.addEdge(4, 6, 6);
graph.addEdge(5, 6, 4);
System.out.println("The following nodes form the shortest paths from node A:");
graph.path();
graph.clear();
}
}

