1. Matrice bidimensionale
Încă un fapt interesant despre matrice. Matricele nu sunt doar unidimensionale (liniare). Ele pot fi, de asemenea, bidimensionale.
Ce înseamnă asta, te întrebi?
Aceasta înseamnă că celulele matricei pot reprezenta nu numai o coloană (sau un rând), ci și un tabel dreptunghiular.
int[][] name = new int[width][height];Unde nume este numele variabilei matricei, lățimea este lățimea tabelului (în celule) și înălțimea este înălțimea tabelului. Exemplu:
|
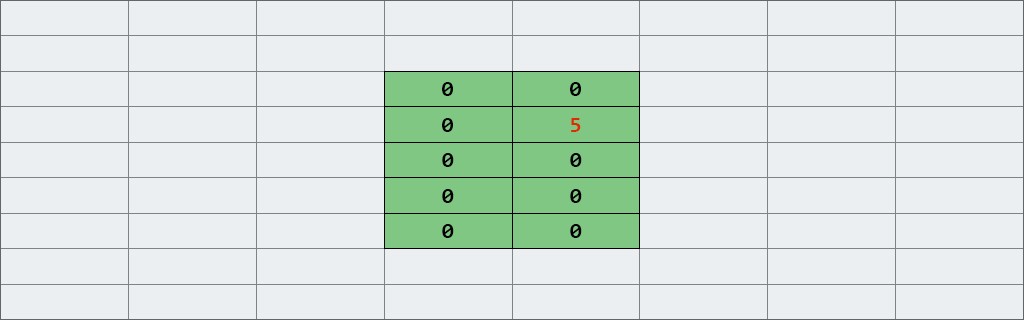
Creăm o matrice bidimensională: 2 coloane și 5 rânduri. Scrieți 5 în celula (1, 1). |
Așa va arăta în memorie:
Apropo, puteți utiliza și inițializarea rapidă pentru matrice bidimensionale:
// Lengths of months of the year in each quarter
int[][] months = { {31, 28, 31}, {30, 31, 30}, {31, 31, 30}, {31, 30, 31} };Există atât de multe locuri în care tu, ca programator, ai putea avea nevoie de o matrice bidimensională. Matricele bidimensionale sunt fundamentul aproape tuturor jocurilor de societate, de exemplu șahul, damele, tic-tac-toe și bătălia pe mare:
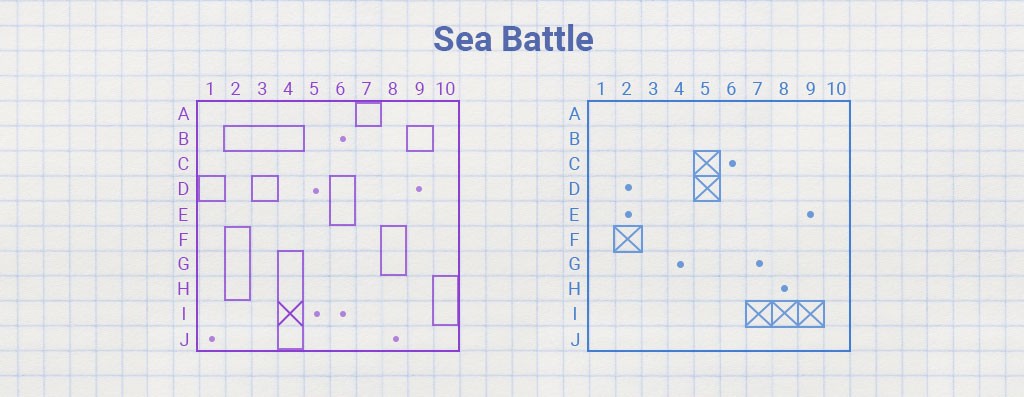
Matricele bidimensionale sunt perfecte pentru șah sau bătălie pe mare. Avem nevoie doar de numere din coordonatele celulei. Nu „pion e2-e4”, ci „pion (5,2) -> (5,4)”. Îți va fi și mai ușor ca programator.
2. Aranjarea elementelor în matrice: (x, y) sau (y, x)
Apropo, există o dilemă interesantă aici:
Când creăm o matrice folosind new int[2][5];, avem un tabel cu „două rânduri și 5 coloane ” sau este „două coloane și 5 rânduri ”?” Cu alte cuvinte, specificăm mai întâi lățimea și apoi înălțimea... sau invers, mai întâi înălțimea și apoi lățimea? Ei bine, așa cum spunem adesea, totul nu este atât de simplu aici.
Să începem cu întrebarea cum este stocată matricea în memorie .
Desigur, memoria computerului nu are de fapt o matrice în ea: fiecare locație din memorie are o adresă numerică secvențială: 0, 1, 2, ... În cazul nostru, vorbim de o matrice 2 × 5, dar în memorie sunt doar 10 celule consecutive, nimic mai mult. Nimic nu indică unde sunt rândurile și coloanele.
Argument în favoarea „lățime x înălțime”.
Argumentul în favoarea acestei abordări este că toată lumea învață matematică la școală, unde învață că perechile de coordonate sunt scrise ca „x” (adică axa orizontală) și apoi „y” (dimensiunea verticală). Și acesta nu este doar un standard școlar - este un standard general acceptat în matematică. După cum se spune, nu te poți certa cu matematica. Chiar așa? Mai întâi lățimea și apoi înălțimea?
Argument în favoarea „înălțime x lățime”.
Există, de asemenea, un argument interesant pentru această poziție: inițializarea rapidă a tablourilor bidimensionale. Într-adevăr, dacă vrem să inițializam matricea noastră, atunci putem scrie cod astfel:
// Matrix of important data
int[][] matrix = { {1, 2, 3, 4, 5}, {1, 2, 3, 4, 5} };Nu observi nimic? Dacă avem asta?
// Matrix of important data
int[][] matrix = {
{1, 2, 3, 4, 5},
{1, 2, 3, 4, 5}
};Dacă ne scriem datele în cod linie cu linie, atunci obținem o matrice cu 2 rânduri și 5 coloane.
Concluzie
Ce putem spune? Depinde de tine să decizi care este mai convenabil pentru tine. Cel mai important lucru este că toți programatorii care lucrează la același proiect respectă aceeași abordare.
Dacă lucrați la un proiect al cărui cod are o mulțime de matrice bidimensionale inițializate, atunci cel mai probabil totul se va baza pe o inițializare rapidă a datelor, adică veți avea standardul „înălțime x lățime”.
Dacă ai norocul să te regăsești într-un proiect care implică multă matematică și lucrează cu coordonate (de exemplu, motoare de joc), atunci codul va adopta cel mai probabil abordarea „lățime x înălțime”.
3. Cum sunt aranjate tablourile bidimensionale
Și acum veți afla cum sunt de fapt aranjate matricele bidimensionale. Gata?
Matricele bidimensionale sunt de fapt matrice de matrice!
Cu alte cuvinte, dacă în cazul unui tablou obișnuit o variabilă de matrice stochează o referință la un container care stochează elemente de matrice, atunci în cazul matricelor bidimensionale situația explodează puțin: o variabilă de matrice bidimensională stochează o referință la un container care stochează referințe la matrice unidimensionale. Este mai bine să o vezi în acțiune o dată decât să încerci să o explic de o sută de ori:
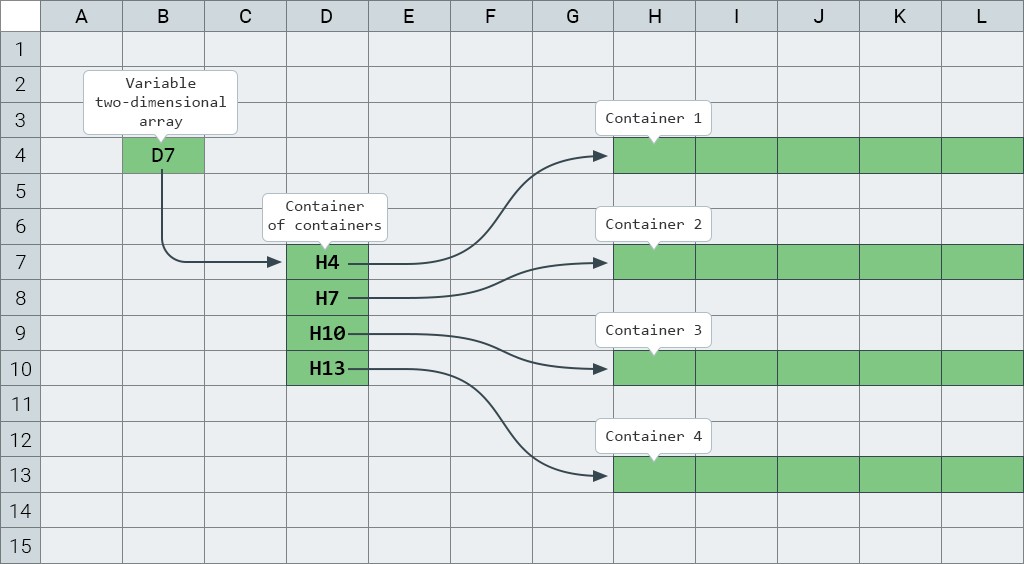
În stânga , avem o variabilă de matrice bidimensională, care stochează o referință la un obiect de matrice bidimensională. Înîn mijloc avem un obiect matrice bidimensională ale cărui celule stochează matrice unidimensionale, care sunt rândurile unei matrice bidimensionale. Și în dreapta , puteți vedea patru matrice unidimensionale - rândurile matricei noastre bidimensionale.
Acesta este modul în care funcționează de fapt matricele bidimensionale. Și această abordare oferă programatorului Java mai multe avantaje:
În primul rând , deoarece un „container de containere” stochează referințe la „matrice de rânduri”, putem schimba foarte rapid și ușor rândurile. Pentru a obține un „container de containere”, trebuie doar să specificați un index în loc de doi. Exemplu:
int[][] data = new int[2][5];
int[] row1 = data[0];
int[] row2 = data[1];Acest cod vă permite să schimbați rândurile:
|
Matricea bidimensională matrix[0]stochează o referință la primul rând. Schimbăm referințele. Ca rezultat, matrixmatricea arată astfel: |
Dacă vă referiți la o celulă a unei matrice bidimensionale, dar specificați doar un index după numele matricei, atunci vă referiți la un container de containere ale căror celule stochează referințe la matrice unidimensionale obișnuite.

GO TO FULL VERSION