1. Matrices bidimensionales
Otro hecho interesante sobre las matrices. Los arreglos no son solo unidimensionales (lineales). También pueden ser bidimensionales.
¿Qué significa eso, preguntas?
Esto significa que las celdas de la matriz pueden representar no solo una columna (o fila), sino también una tabla rectangular.
int[][] name = new int[width][height];Donde name es el nombre de la variable de matriz, width es el ancho de la tabla (en celdas) y height es la altura de la tabla. Ejemplo:
|
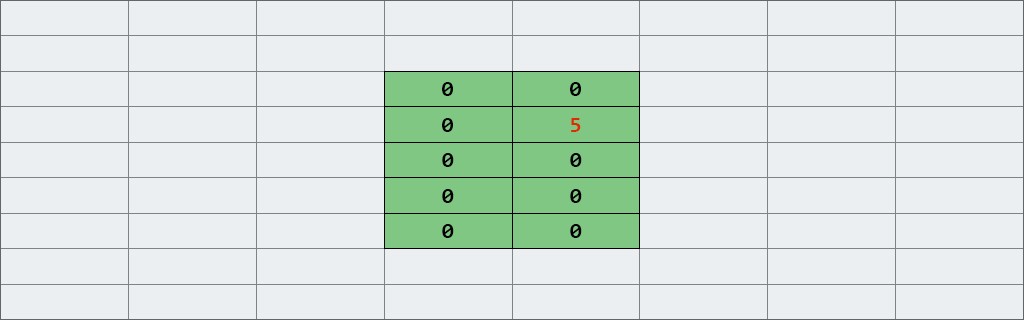
Creamos una matriz bidimensional: 2 columnas y 5 filas. Escriba 5 en la celda (1, 1). |
Así es como se verá en la memoria:
Por cierto, también puede usar la inicialización rápida para matrices bidimensionales:
// Lengths of months of the year in each quarter
int[][] months = { {31, 28, 31}, {30, 31, 30}, {31, 31, 30}, {31, 30, 31} };Hay tantos lugares donde usted, como programador, podría necesitar una matriz bidimensional. Las matrices bidimensionales son la base de casi todos los juegos de mesa, por ejemplo, ajedrez, damas, tic-tac-toe y batalla naval:
Las matrices bidimensionales son perfectas para el ajedrez o la batalla naval. Solo necesitamos números de coordenadas de celda. No 'peón e2-e4', sino 'peón (5,2) -> (5,4)'. Será aún más fácil para ti como programador.
2. Organizar elementos en matrices: (x, y) o (y, x)
Por cierto, hay un dilema interesante aquí:
Cuando creamos una matriz usando new int[2][5];, ¿tenemos una tabla de 'dos filas y 5 columnas ' o es 'dos columnas y 5 filas '?" En otras palabras, ¿estamos especificando primero el ancho y luego la altura... o viceversa, ¿primero el alto y luego el ancho? Bueno, como solemos decir, aquí no todo es tan simple.
Comencemos con la pregunta de cómo se almacena la matriz en la memoria .
Por supuesto, la memoria de la computadora en realidad no tiene una matriz: cada ubicación en la memoria tiene una dirección numérica secuencial: 0, 1, 2, ... En nuestro caso, hablamos de una matriz de 2 × 5, pero en la memoria son solo 10 celdas consecutivas, nada más. Nada indica dónde están las filas y las columnas.
Argumento a favor de "ancho x alto".
El argumento a favor de este enfoque es que todos aprenden matemáticas en la escuela, donde aprenden que los pares de coordenadas se escriben como 'x' (es decir, el eje horizontal) y luego 'y' (la dimensión vertical). Y esto no es solo un estándar escolar, es un estándar generalmente aceptado en matemáticas. Como dicen, no se puede discutir con las matemáticas. ¿Es eso así? Primero ancho y luego alto?
Argumento a favor de "alto x ancho".
También hay un argumento interesante para esta posición: inicialización rápida de matrices bidimensionales. De hecho, si queremos inicializar nuestra matriz, podemos escribir un código como este:
// Matrix of important data
int[][] matrix = { {1, 2, 3, 4, 5}, {1, 2, 3, 4, 5} };¿No notas nada? ¿Y si tenemos esto?
// Matrix of important data
int[][] matrix = {
{1, 2, 3, 4, 5},
{1, 2, 3, 4, 5}
};Si escribimos nuestros datos en el código línea por línea, obtenemos una matriz con 2 filas y 5 columnas.
Línea de fondo
¿Qué podemos decir? Depende de usted decidir cuál es más conveniente para usted. Lo más importante es que todos los programadores que trabajan en el mismo proyecto sigan el mismo enfoque.
Si trabaja en un proyecto cuyo código tiene muchas matrices bidimensionales inicializadas, lo más probable es que todo se base en una inicialización rápida de datos, es decir, tendrá el estándar 'alto x ancho'.
Si tiene la suerte de encontrarse en un proyecto que involucra muchas matemáticas y trabaja con coordenadas (por ejemplo, motores de juegos), lo más probable es que el código adopte el enfoque de 'ancho x alto'.
3. Cómo se organizan los arreglos bidimensionales
Y ahora aprenderá cómo se organizan realmente los arreglos bidimensionales. ¿Listo?
¡Los arreglos bidimensionales son en realidad arreglos de arreglos!
En otras palabras, si en el caso de un arreglo ordinario una variable de arreglo almacena una referencia a un contenedor que almacena elementos de arreglo, entonces en el caso de arreglos bidimensionales la situación estalla un poco: una variable de arreglo bidimensional almacena un referencia a un contenedor que almacena referencias a matrices unidimensionales. Es mejor verlo en acción una vez que tratar de explicarlo cien veces:
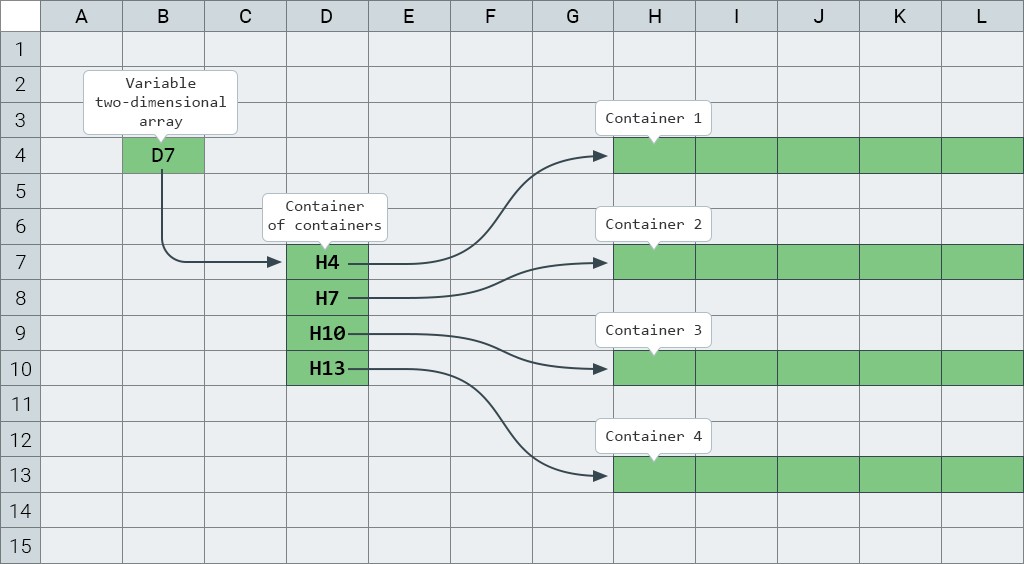
A la izquierda , tenemos una variable de matriz bidimensional, que almacena una referencia a un objeto de matriz bidimensional. En elen el medio tenemos un objeto de matriz bidimensional cuyas celdas almacenan matrices unidimensionales, que son las filas de una matriz bidimensional. Y a la derecha , puede ver cuatro matrices unidimensionales: las filas de nuestra matriz bidimensional.
Así es como funcionan realmente las matrices bidimensionales. Y este enfoque le da al programador de Java varias ventajas:
Primero , dado que un 'contenedor de contenedores' almacena referencias a 'matrices de filas', podemos intercambiar filas de manera muy rápida y sencilla. Para obtener un 'contenedor de contenedores', solo necesita especificar un índice en lugar de dos. Ejemplo:
int[][] data = new int[2][5];
int[] row1 = data[0];
int[] row2 = data[1];Este código te permite intercambiar filas:
|
La matriz bidimensional matrix[0]almacena una referencia a la primera fila. Intercambiamos las referencias. Como resultado, la matrixmatriz se ve así: |
Si hace referencia a una celda de una matriz bidimensional, pero solo especifica un índice después del nombre de la matriz, entonces se refiere a un contenedor de contenedores cuyas celdas almacenan referencias a matrices unidimensionales ordinarias.

GO TO FULL VERSION