Two-dimensional arrays

1. Two-dimensional arrays

One more interesting fact about arrays. Arrays are not only one-dimensional (linear). They can also be two-dimensional.

What does that mean, you ask?

This means that the cells of the array can represent not only a column (or row), but also a rectangular table.

int[][] name = new int[width][height];

Where name is the name of the array variable, width is the table width (in cells), and height is the table height. Example:

int[][] data = new int[2][5];
data[1][1] = 5;

This is how it will look in memory:

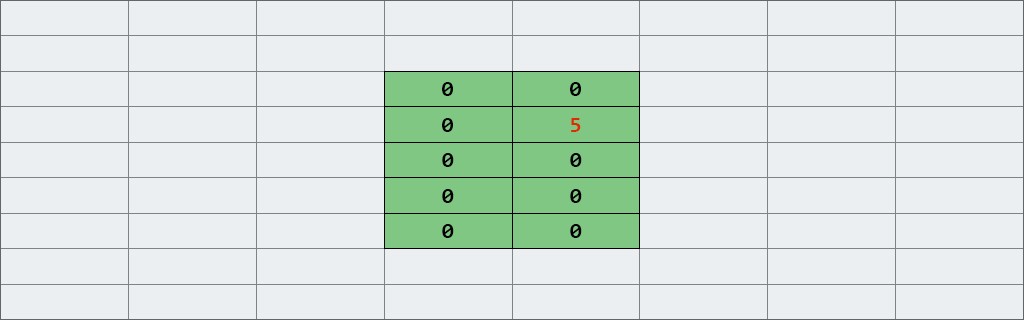
By the way, you can also use fast initialization for two-dimensional arrays:

// Lengths of months of the year in each quarter
int[][] months = { {31, 28, 31}, {30, 31, 30}, {31, 31, 30}, {31, 30, 31} };

There are so many places where you, as a programmer, might need a two-dimensional array. Two-dimensional arrays are the foundation of almost every board game, e.g. chess, checkers, tic-tac-toe, and sea battle:

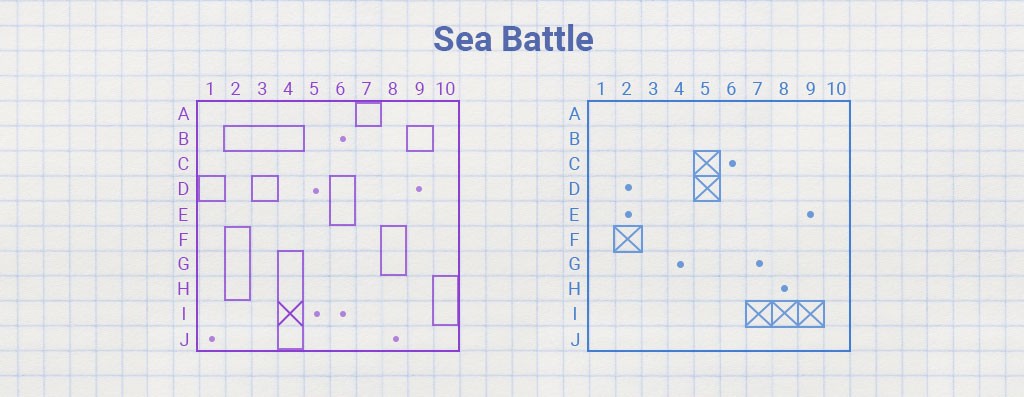
Two-dimensional arrays are the perfect for chess or sea battle. We only need numbers form cell coordinates. Not 'pawn e2-e4', but 'pawn (5,2) -> (5,4)'. It will be even easier for you as a programmer.

2. Arranging elements in arrays: (x, y) or (y, x)

By the way, there's an interesting dilemma here:

When we create an array using new int[2][5];, do we have a table of 'two rows and 5 columns' or is it 'two columns and 5 rows'?" In other words, are we first specifying the width and then the height... or vice versa, first the height and then the width? Well, as we often say, everything is not so simple here.

Let's start with the question of how the array is stored in memory.

Of course, computer memory doesn't actually have a matrix in it: each location in memory has a sequential numeric address: 0, 1, 2, ... In our case, we speak of a 2 × 5 matrix, but in memory it is just 10 consecutive cells, nothing more. Nothing indicates where the rows and columns are.

Argument in favor of "width x height".

The argument in favor of this approach is this that everyone learns math in school, where they learn that coordinate pairs are written as 'x' (that is, the horizontal axis) and then 'y' (the vertical dimension). And this is not just a school standard — it's a generally accepted standard in mathematics. As they say, you can't argue with math. Is that so? First width and then height?

Argument in favor of "height x width".

There's also an interesting argument to be made for this position: fast initialization of two-dimensional arrays. Indeed, if we want to initialize our array, then we can write code like this:

// Matrix of important data
int[][] matrix = { {1, 2, 3, 4, 5}, {1, 2, 3, 4, 5} };

Don't you notice anything? What if we have this?

// Matrix of important data
int[][] matrix = {
  {1, 2, 3, 4, 5},
  {1, 2, 3, 4, 5}
};

If we write our data in the code line by line, then we get a matrix with 2 rows and 5 columns.

Bottom line

What can we say? It's up to you to decide which is more convenient for you. The most important thing is that all programmers working on the same project stick to the same approach.

If you work on a project whose code has lots of initialized two-dimensional arrays, then most likely everything there will be based on fast data initialization, i.e. you'll have the standard 'height x width'.

If you are lucky enough to find yourself in a project involving a lot of mathematics and working with coordinates (for example, game engines), then the code will most likely adopt the 'width x height' approach.

3. How two-dimensional arrays are arranged

And now you will learn how two-dimensional arrays are actually arranged. Ready?

Two-dimensional arrays are actually arrays of arrays!

In other words, if in the case of an ordinary array an array variable stores a reference to a container that stores array elements, then in the case of two-dimensional arrays the situation explodes a little: a two-dimensional-array variable stores a reference to a container that stores references to one-dimensional arrays. It's better to see it in action once rather than try to explain it a hundred times:

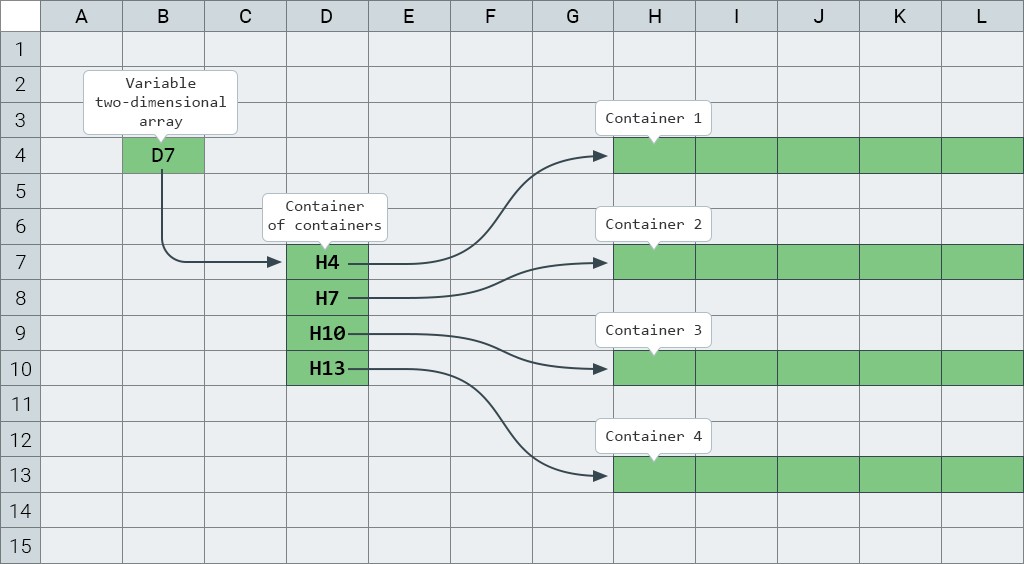
On the left, we have a two-dimensional-array variable, which stores a reference to a two-dimensional-array object. In the middle we have a two-dimensional array object whose cells store one-dimensional arrays, which are the rows of a two-dimensional array. And on the right, you can see four one-dimensional arrays — the rows of our two-dimensional array.

This is how two-dimensional arrays actually work. And this approach gives the Java programmer several advantages:

First, since a 'container of containers' stores references to 'arrays of rows', we can very quickly and easily swap rows. To get a 'container of containers', you just need to specify one index instead of two. Example:

int[][] data = new int[2][5];
int[] row1 = data[0];
int[] row2 = data[1];

This code lets you swap rows:

// Matrix of important data
int[][] matrix = {
  {1, 2, 3, 4, 5},
  {5, 4, 3, 2, 1}
};

int[] tmp = matrix[0];
matrix[0] = matrix[1];
matrix[1] = tmp;

{
  {5, 4, 3, 2, 1},
  {1, 2, 3, 4, 5}
};

If you refer to a cell of a two-dimensional array, but you only specify one index after the name of the array, then you are referring to a container of containers whose cells store references to ordinary one-dimensional arrays.