1. Matrizes bidimensionais
Mais um fato interessante sobre arrays. Arrays não são apenas unidimensionais (lineares). Eles também podem ser bidimensionais.
O que significa isso, você pergunta?
Isso significa que as células da matriz podem representar não apenas uma coluna (ou linha), mas também uma tabela retangular.
int[][] name = new int[width][height];Onde name é o nome da variável de array, width é a largura da tabela (em células) e height é a altura da tabela. Exemplo:
|
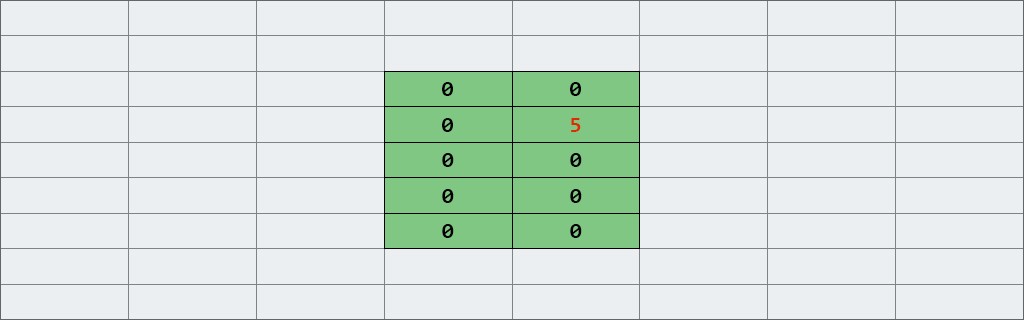
Criamos um array bidimensional: 2 colunas e 5 linhas. Escreva 5 na célula (1, 1). |
É assim que ficará na memória:
A propósito, você também pode usar a inicialização rápida para arrays bidimensionais:
// Lengths of months of the year in each quarter
int[][] months = { {31, 28, 31}, {30, 31, 30}, {31, 31, 30}, {31, 30, 31} };Existem tantos lugares onde você, como programador, pode precisar de um array bidimensional. Matrizes bidimensionais são a base de quase todos os jogos de tabuleiro, por exemplo, xadrez, damas, jogo da velha e batalha naval:
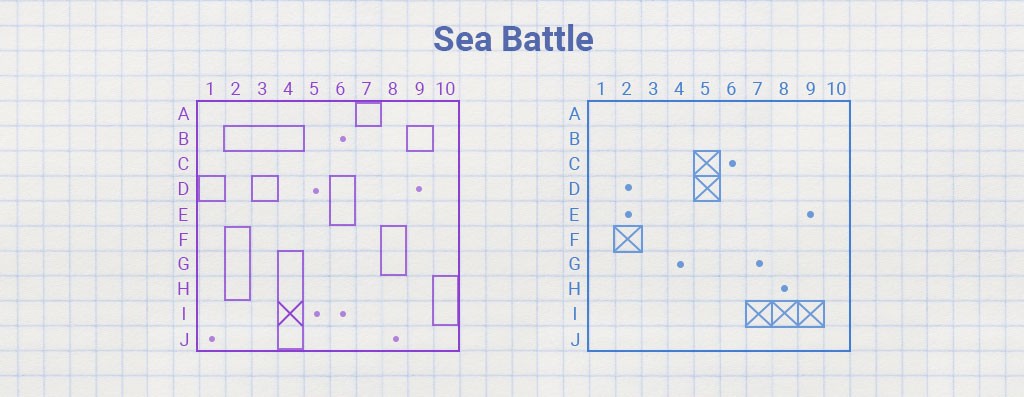
Matrizes bidimensionais são perfeitas para xadrez ou batalha naval. Nós só precisamos de números de coordenadas celulares. Não 'peão e2-e4', mas 'peão (5,2) -> (5,4)'. Será ainda mais fácil para você como programador.
2. Organizando elementos em matrizes: (x, y) ou (y, x)
A propósito, há um dilema interessante aqui:
Quando criamos um array usando new int[2][5];, temos uma tabela de 'duas linhas e 5 colunas ' ou é 'duas colunas e 5 linhas '?" Em outras palavras, estamos primeiro especificando a largura e depois a altura... ou vice-versa, primeiro a altura e depois a largura? Bem, como costumamos dizer, nem tudo é tão simples aqui.
Vamos começar com a questão de como o array é armazenado na memória .
É claro que a memória do computador não contém uma matriz: cada local na memória possui um endereço numérico sequencial: 0, 1, 2, ... No nosso caso, falamos de uma matriz 2 × 5, mas na memória são apenas 10 células consecutivas, nada mais. Nada indica onde estão as linhas e colunas.
Argumento a favor de "largura x altura".
O argumento a favor dessa abordagem é que todos aprendem matemática na escola, onde aprendem que os pares de coordenadas são escritos como 'x' (ou seja, o eixo horizontal) e depois 'y' (a dimensão vertical). E este não é apenas um padrão escolar – é um padrão geralmente aceito em matemática. Como dizem, você não pode discutir com a matemática. É assim mesmo? Primeiro largura e depois altura?
Argumento a favor de "altura x largura".
Há também um argumento interessante a ser feito para essa posição: inicialização rápida de arrays bidimensionais. De fato, se quisermos inicializar nosso array, podemos escrever um código como este:
// Matrix of important data
int[][] matrix = { {1, 2, 3, 4, 5}, {1, 2, 3, 4, 5} };Você não percebe nada? E se tivermos isso?
// Matrix of important data
int[][] matrix = {
{1, 2, 3, 4, 5},
{1, 2, 3, 4, 5}
};Se escrevermos nossos dados no código linha por linha, obteremos uma matriz com 2 linhas e 5 colunas.
Resumindo
O que podemos dizer? Cabe a você decidir qual é mais conveniente para você. O mais importante é que todos os programadores que trabalham no mesmo projeto sigam a mesma abordagem.
Se você trabalha em um projeto cujo código possui muitos arrays bidimensionais inicializados, provavelmente tudo ali será baseado na inicialização rápida de dados, ou seja, você terá o padrão 'altura x largura'.
Se você tiver a sorte de se encontrar em um projeto envolvendo muita matemática e trabalhando com coordenadas (por exemplo, mecanismos de jogos), o código provavelmente adotará a abordagem 'largura x altura'.
3. Como as matrizes bidimensionais são organizadas
E agora você aprenderá como as matrizes bidimensionais são realmente organizadas. Preparar?
Arrays bidimensionais são, na verdade, arrays de arrays!
Em outras palavras, se no caso de um array comum uma variável de array armazena uma referência a um container que armazena elementos de array, então no caso de arrays bidimensionais a situação explode um pouco: uma variável de array bidimensional armazena um referência a um contêiner que armazena referências a matrizes unidimensionais. É melhor vê-lo em ação uma vez do que tentar explicá-lo centenas de vezes:
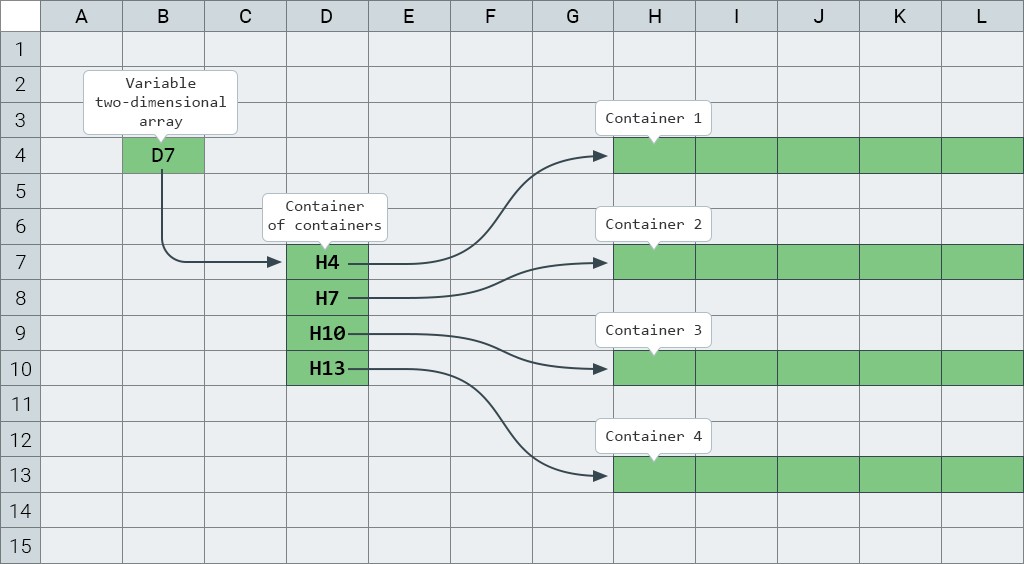
À esquerda , temos uma variável de matriz bidimensional, que armazena uma referência a um objeto de matriz bidimensional. Nomeio temos um objeto array bidimensional cujas células armazenam arrays unidimensionais, que são as linhas de um array bidimensional. E à direita , você pode ver quatro arrays unidimensionais — as linhas de nosso array bidimensional.
É assim que os arrays bidimensionais realmente funcionam. E esta abordagem dá ao programador Java várias vantagens:
Primeiro , como um 'container de contêineres' armazena referências a 'arrays de linhas', podemos trocar as linhas de maneira muito rápida e fácil. Para obter um 'contêiner de contêineres', você só precisa especificar um índice em vez de dois. Exemplo:
int[][] data = new int[2][5];
int[] row1 = data[0];
int[] row2 = data[1];Este código permite trocar linhas:
|
A matriz bidimensional matrix[0]armazena uma referência à primeira linha. Trocamos as referências. Como resultado, a matrixmatriz se parece com isso: |
Se você se referir a uma célula de uma matriz bidimensional, mas especificar apenas um índice após o nome da matriz, estará se referindo a um contêiner de contêineres cujas células armazenam referências a matrizes unidimensionais comuns.

GO TO FULL VERSION