здрасти Днешният урок ще бъде малко по-различен от останалите. Ще се различава по това, че е само косвено свързан с Java. Въпреки това тази тема е много важна за всеки програмист. Ще говорим за алгоритми . Какво е алгоритъм? С прости думи, това е няHowва последователност от действия, които трябва да бъдат изпълнени, за да се постигне желаният резултат . Често използваме алгоритми в ежедневието. Например, всяка сутрин имате конкретна задача: отидете на учorще or на работа и в същото време бъдете:
Облечени
Чисто
Fed
Какъв алгоритъм ви позволява да постигнете този резултат?
Събудете се с помощта на будилник.
Вземете душ и се измийте.
Направете закуска и малко кафе or чай.
Яжте.
Ако не сте изгладor дрехите си предишната вечер, изгладете ги.
Облечи се.
Напусни къщата.
Тази последователност от действия определено ще ви позволи да постигнете желания резултат. В програмирането ние непрекъснато работим за изпълнение на задачи. Значителна част от тези задачи могат да бъдат изпълнени с помощта на вече известни алгоритми. Да предположим например, че задачата ви е следната: сортирайте списък от 100 имена в масив . Тази задача е доста проста, но може да бъде решена по различни начини. Ето едно възможно решение: Алгоритъм за сортиране на имена по азбучен ред:
Купете or изтеглете изданието от 1961 г. на Третия нов международен речник на Webster.
Намерете всяко име от нашия списък в този речник.
На лист хартия напишете pageта от речника, на която се намира името.
Използвайте листчетата, за да сортирате имената.
Дали такава последователност от действия ще изпълни нашата задача? Да, със сигурност ще стане. Ефективно ли е това решение ? Едва ли. Тук стигаме до друг много важен аспект на алгоритмите: тяхната ефективност . Има няколко начина за изпълнение на тази задача. Но Howто в програмирането, така и в обикновения живот, ние искаме да изберем най-ефективния начин. Ако задачата ви е да направите намазано с масло парче препечен хляб, можете да започнете със засяване на пшеница и издояване на крава. Но това би било неефективнорешение — ще отнеме много време и ще струва много пари. Можете да изпълните простата си задача, като просто купите хляб и масло. Въпреки че ви позволява да разрешите проблема, алгоритъмът, включващ пшеница и крава, е твърде сложен, за да се използва на практика. В програмирането имаме специална нотация, наречена голяма О нотация, за оценка на сложността на алгоритмите. Big O дава възможност да се оцени колко времето за изпълнение на алгоритъма зависи от размера на входните данни . Нека разгледаме най-простия пример: трансфер на данни. Представете си, че трябва да изпратите няHowва информация под формата на файл на голямо разстояние (например 5000 мor). Какъв алгоритъм би бил най-ефективен? Зависи от данните, с които работите. Да предположим например, че имаме аудио файл, който е 10 MB. В този случай най-ефективният алгоритъм е да изпратите file през интернет. Не може да отнеме повече от няколко minutesи! Нека преформулираме нашия алгоритъм: "Ако искате да прехвърлите информация под формата на файлове на разстояние от 5000 мor, трябва да изпратите данните през Интернет". Отлично. Сега нека го анализираме. Изпълнява ли задачата ни?Е, да, така е. Но Howво можем да кажем за неговата сложност? Хм, сега нещата стават по-интересни. Факт е, че нашият алгоритъм е много зависим от входните данни, а именно от размера на файловете. Ако имаме 10 мегаbyteа, значи всичко е наред. Но Howво ще стане, ако трябва да изпратим 500 мегаbyteа? 20 гигаbyteа? 500 тераbyteа? 30 петаbyteа? Дали алгоритъмът ни ще спре да работи? Не, всички тези количества данни наистина могат да бъдат прехвърлени. Ще отнеме ли повече време? Да, ще стане! Сега знаем важна характеристика на нашия алгоритъм: колкото по-голямо е количеството данни за изпращане, толкова по-дълго ще отнеме изпълнението на алгоритъма. Но бихме искали да имаме по-точно разбиране на тази връзка (между размера на входните данни и времето, необходимо за изпращането им). В нашия случай алгоритмичната сложност е линейна . „Линеен“ означава, че с увеличаването на количеството входни данни времето, необходимо за изпращането им, ще се увеличи приблизително пропорционално. Ако количеството данни се удвои, тогава времето, необходимо за изпращането им, ще бъде два пъти повече. Ако данните се увеличат 10 пъти, тогава времето за предаване ще се увеличи 10 пъти. Използвайки нотация голямо O, сложността на нашия алгоритъм се изразява като O(n). Трябва да запомните тази нотация за в бъдеще — тя винаги се използва за алгоритми с линейна сложност. Обърнете внимание, че не говорим за няколко неща, които може да варират тук: скорост на интернет, изчислителна мощност на нашия компютър и т.н. Когато оценяваме сложността на даден алгоритъм, просто няма смисъл да вземаме предвид тези фактори — във всеки случай те са извън нашия контрол. Нотацията Big O изразява сложността на самия алгоритъм, а не "средата", в която той работи. Нека продължим с нашия пример. Да предположим, че в крайна сметка научим, че трябва да изпратим файлове с общо 800 тераbyteа. Можем, разбира се, да изпълним задачата си, като ги изпратим по интернет. Има само един проблем: при стандартни битови скорости на предаване на данни (100 мегабита в секунда), това ще отнеме приблизително 708 дни. Почти 2 години! :O Нашият алгоритъм очевидно не е подходящ тук. Имаме нужда от друго решение! Неочаквано ИТ гигантът Amazon ни идва на помощ! Услугата Snowmobile на Amazon ни позволява да качваме голямо количество данни в мобилно хранorще и след това да ги доставяме до желания address с камион! И така, имаме нов алгоритъм! „Ако искате да прехвърлите информация под формата на файлове на разстояние от 5000 мor и това ще отнеме повече от 14 дни за изпращане през интернет, трябва да изпратите данните на камион на Amazon.“ Тук произволно избрахме 14 дни. Да кажем, че това е най-дългият период, който можем да чакаме. Нека анализираме нашия алгоритъм. Какво ще кажете за скоростта му? Дори камионът да се движи само с 50 мor в час, той ще измине 5000 мor само за 100 часа. Това са малко повече от четири дни! Това е много по-добре от опцията за изпращане на данните през интернет. А Howво да кажем за сложността на този алгоритъм? Също така ли е линеен, т.е. O(n)? Не, не е. В края на краищата камионът не се интересува колко тежко го натоварвате — той все пак ще се движи с приблизително същата скорост и ще пристигне навреме. Независимо дали имаме 800 тераbyteа or 10 пъти повече, камионът все още ще стигне до местонаmeaningто си в рамките на 5 дни. С други думи, базираният на камион алгоритъм за пренос на данни има постоянна сложност. Тук "константа" означава, че не зависи от размера на входните данни. Поставете 1GB флашка в камиона, ще пристигне до 5 дни. Поставете в дискове, съдържащи 800 тераbyteа данни, те ще пристигнат в рамките на 5 дни. Когато се използва нотация с голямо O, постоянната сложност се означава с O(1) . Запознахме се с O(n) и O(1) , така че сега нека да разгледаме още примери в света на програмирането :) Да предположим, че ви е даден масив от 100 числа и задачата е да изведете всяко от тях на конзолата. Пишете обикновен forцикъл, който изпълнява тази задача
int[] numbers =newint[100];// ...fill the array with numbersfor(int i: numbers){System.out.println(i);}
Каква е сложността на този алгоритъм? Линеен, т.е. O(n). Броят на действията, които програмата трябва да извърши, зависи от това колко числа са й предадени. Ако има 100 числа в масива, ще има 100 действия (операции за показване на низове на екрана). Ако в масива има 10 000 числа, трябва да се извършат 10 000 действия. Може ли нашият алгоритъм да бъде подобрен по няHowъв начин? Не. Независимо от всичко, ще трябва да направим N преминавания през масива и да изпълним N оператора, за да покажем низове на конзолата. Помислете за друг пример.
Имаме празен LinkedList, в който вмъкваме няколко числа. Трябва да оценим алгоритмичната сложност на вмъкването на едно число в LinkedListнашия пример и How то зависи от броя на елементите в списъка. Отговорът е O(1), т.е. постоянна сложност . Защо? Обърнете внимание, че вмъкваме всяко число в началото на списъка. Освен това ще си спомните, че когато вмъкнете число в LinkedList, елементите не се местят никъде. Връзките (or препратките) се актуализират (ако сте забравor How работи LinkedList, вижте един от нашите стари уроци ). Ако първото число в нашия списък е xи вмъкнем числото y в началото на списъка, тогава всичко, което трябва да направим, е следното:
x.previous = y;
y.previous =null;
y.next = x;
Когато актуализираме връзките, не ни интересува колко числа вече има вLinkedList , независимо дали едно or един мorард. Сложността на алгоритъма е постоянна, т.е. O(1).
Логаритмична сложност
Не изпадайте в паника! :) Ако думата "логаритмичен" ви кара да искате да затворите този урок и да спрете да четете, просто изчакайте няколко minutesи. Тук няма да има луда математика (има много обяснения като това другаде) и ще отделим всеки пример. Представете си, че вашата задача е да намерите едно конкретно число в масив от 100 числа. По-точно, трябва да проверите дали е там or не. Веднага щом търсеният номер бъде намерен, търсенето приключва и вие показвате следното в конзолата: „Трябваното число беше намерено! Неговият индекс в масива = ....“ Как бихте изпълнor тази задача? Тук решението е очевидно: трябва да итерирате елементите на масива един по един, като започнете от първия (or от последния) и да проверите дали текущото число съвпада с това, което търсите. Съответно броят на действията зависи пряко от броя на елементите в масива. Ако имаме 100 числа, тогава може да се наложи да отидем до следващия елемент 100 пъти и да извършим 100 сравнения. Ако има 1000 числа, тогава може да има 1000 сравнения. Това очевидно е линейна сложност, т.еO(n) . А сега ще добавим едно уточнение към нашия пример: масивът, в който трябва да намерите числото, е сортиран във възходящ ред . Това променя ли нещо по отношение на нашата задача? Все още можем да извършим грубо търсене на желания номер. Но като алтернатива можем да използваме добре познатия алгоритъм за двоично търсене .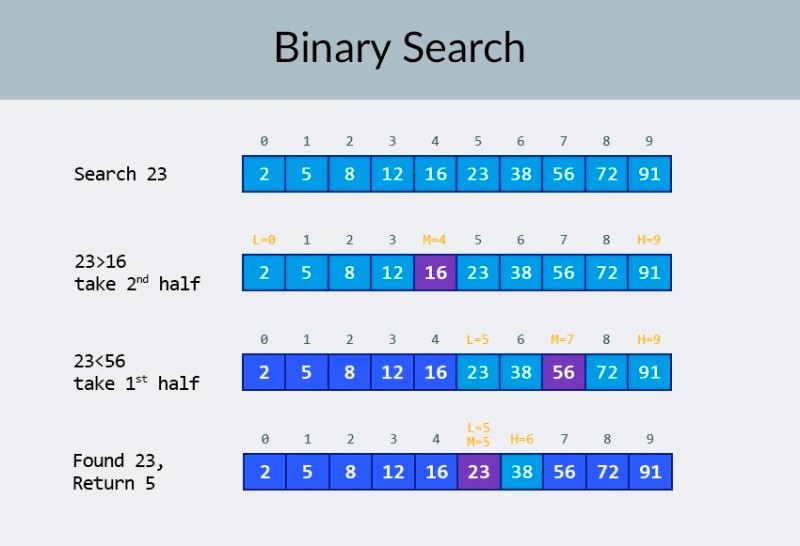 В горния ред на изображението виждаме сортиран масив. Трябва да намерим числото 23 в него. Вместо да обикаляме числата, ние просто разделяме масива на 2 части и проверяваме средното число в масива. Намерете числото, което се намира в клетка 4 и го проверете (втори ред на изображението). Това число е 16, а ние търсим 23. Текущият брой е по-малък от това, което търсим. Какво означава това? Означава, чевсички предишни числа (тези, които се намират преди числото 16) не трябва да се проверяват : те гарантирано са по-малки от това, което търсим, защото нашият масив е сортиран! Продължаваме търсенето сред останалите 5 елемента. Забележка:направихме само едно сравнение, но вече сме елиминирали половината от възможните опции. Остават ни само 5 елемента. Ще повторим нашата предишна стъпка, като отново разделим оставащия подмасив наполовина и отново вземем средния елемент (3-тия ред в изображението). Числото е 56 и е по-голямо от това, което търсим. Какво означава това? Това означава, че сме елиминирали още 3 възможности: самото число 56, Howто и двете числа след него (тъй като те гарантирано са по-големи от 23, тъй като масивът е сортиран). Остават ни само 2 числа за проверка (последния ред в изображението) — числата с индекси на масива 5 и 6. Проверяваме първото от тях и намираме това, което търсихме — числото 23! Индексът му е 5! Нека да разгледаме резултатите от нашия алгоритъм и тогава ще ще анализира неговата сложност. Между другото, сега разбирате защо това се нарича двоично търсене: то разчита на многократно разделяне на данните наполовина. Резултатът е впечатляващ! Ако използвахме линейно търсене, за да търсим числото, ще ни трябват до 10 сравнения, но с двоично търсене изпълнихме задачата само с 3! В най-лошия случай ще има 4 сравнения (ако в последната стъпка числото, което искахме, беше второто от останалите възможности, а не първото. И така, Howво ще кажете за неговата сложност? Това е много интересен момент :) Алгоритъмът за двоично търсене е много по-малко зависим от броя на елементите в масива, отколкото алгоритъмът за линейно търсене (тоест проста итерация). С 10 елемента в масива линейното търсене ще се нуждае от максимум 10 сравнения, но двоичното търсене ще се нуждае от максимум 4 сравнения. Това е разлика с коефициент 2,5. Но за масив от 1000 елемента , линейното търсене ще се нуждае от до 1000 сравнения, но двоичното търсене ще изисква само 10 ! Разликата вече е 100 пъти! Забележка:броят на елементите в масива се е увеличил 100 пъти (от 10 на 1000), но броят на сравненията, необходими за двоично търсене, се е увеличил само с коефициент 2,5 (от 4 на 10). Ако стигнем до 10 000 елемента , разликата ще бъде още по-впечатляваща: 10 000 сравнения за линейно търсене и общо 14 сравнения за двоично търсене. И отново, ако броят на елементите се увеличи 1000 пъти (от 10 на 10 000), тогава броят на сравненията се увеличава само с коефициент 3,5 (от 4 на 14). Сложността на алгоритъма за двоично търсене е логаритмична or, ако използваме нотация голямо O, O(log n). Защо се казва така? Логаритъмът е като обратното на степенуването. Двоичният логаритъм е степента, на която трябва да се повдигне числото 2, за да се получи число. Например, имаме 10 000 елемента, които трябва да търсим с помощта на алгоритъма за двоично търсене. В момента можете да погледнете tableта със стойности, за да знаете, че това ще изисква максимум 14 сравнения. Но Howво ще стане, ако никой не е предоставил такава table и трябва да изчислите точния максимален брой сравнения? Просто трябва да отговорите на един прост въпрос: на Howва степен трябва да повдигнете числото 2, така че резултатът да е по-голям or equals на броя на проверяваните елементи? За 10 000 това е 14-та степен. 2 на 13-та степен е твърде малко (8192), но 2 на 14-та степен = 16384, и това число удовлетворява нашето condition (то е по-голямо or равно на броя на елементите в масива). Намерихме логаритъма: 14. Ето от колко сравнения може да имаме нужда! :) Алгоритмите и алгоритмичната сложност е твърде обширна тема, за да се побере в един урок. Но да го знаете е много важно: много интервюта за работа ще включват въпроси, включващи алгоритми. За теория мога да ти препоръчам някои книги. Можете да започнете с " Алгоритми на Grokking ". Примерите в тази книга са написани на Python, но книгата използва много прост език и примери. Това е най-добрият вариант за начинаещ и освен това не е много голям. Сред по-сериозното четиво имаме книги на Робърт Лафор и Робърт Седжуик. И двете са написани на Java, което ще направи ученето малко по-лесно за вас. В крайна сметка вие сте добре запознати с този език! :) За ученици с добри математически умения най-добрият вариант е книгата на Томас Кормен . Но само теория няма да ви напълни корема! Знание! = Способност . Можете да практикувате решаване на проблеми, включващи алгоритми на HackerRank и LeetCode . Задачи от тези уебсайтове често се използват дори по време на интервюта в Google и Facebook, така че определено няма да ви е скучно :) За да затвърдите този материал от урока, ви препоръчвам да гледате това отлично видео за нотацията с голямо О в YouTube. Ще се видим в следващите уроци! :)
Въпреки това тази тема е много важна за всеки програмист. Ще говорим за алгоритми . Какво е алгоритъм? С прости думи, това е няHowва последователност от действия, които трябва да бъдат изпълнени, за да се постигне желаният резултат . Често използваме алгоритми в ежедневието. Например, всяка сутрин имате конкретна задача: отидете на учorще or на работа и в същото време бъдете:
В този случай най-ефективният алгоритъм е да изпратите file през интернет. Не може да отнеме повече от няколко minutesи! Нека преформулираме нашия алгоритъм: "Ако искате да прехвърлите информация под формата на файлове на разстояние от 5000 мor, трябва да изпратите данните през Интернет". Отлично. Сега нека го анализираме. Изпълнява ли задачата ни?Е, да, така е. Но Howво можем да кажем за неговата сложност? Хм, сега нещата стават по-интересни. Факт е, че нашият алгоритъм е много зависим от входните данни, а именно от размера на файловете. Ако имаме 10 мегаbyteа, значи всичко е наред. Но Howво ще стане, ако трябва да изпратим 500 мегаbyteа? 20 гигаbyteа? 500 тераbyteа? 30 петаbyteа? Дали алгоритъмът ни ще спре да работи? Не, всички тези количества данни наистина могат да бъдат прехвърлени. Ще отнеме ли повече време? Да, ще стане! Сега знаем важна характеристика на нашия алгоритъм: колкото по-голямо е количеството данни за изпращане, толкова по-дълго ще отнеме изпълнението на алгоритъма. Но бихме искали да имаме по-точно разбиране на тази връзка (между размера на входните данни и времето, необходимо за изпращането им). В нашия случай алгоритмичната сложност е линейна . „Линеен“ означава, че с увеличаването на количеството входни данни времето, необходимо за изпращането им, ще се увеличи приблизително пропорционално. Ако количеството данни се удвои, тогава времето, необходимо за изпращането им, ще бъде два пъти повече. Ако данните се увеличат 10 пъти, тогава времето за предаване ще се увеличи 10 пъти. Използвайки нотация голямо O, сложността на нашия алгоритъм се изразява като O(n). Трябва да запомните тази нотация за в бъдеще — тя винаги се използва за алгоритми с линейна сложност. Обърнете внимание, че не говорим за няколко неща, които може да варират тук: скорост на интернет, изчислителна мощност на нашия компютър и т.н. Когато оценяваме сложността на даден алгоритъм, просто няма смисъл да вземаме предвид тези фактори — във всеки случай те са извън нашия контрол. Нотацията Big O изразява сложността на самия алгоритъм, а не "средата", в която той работи. Нека продължим с нашия пример. Да предположим, че в крайна сметка научим, че трябва да изпратим файлове с общо 800 тераbyteа. Можем, разбира се, да изпълним задачата си, като ги изпратим по интернет. Има само един проблем: при стандартни битови скорости на предаване на данни (100 мегабита в секунда), това ще отнеме приблизително 708 дни. Почти 2 години! :O Нашият алгоритъм очевидно не е подходящ тук. Имаме нужда от друго решение! Неочаквано ИТ гигантът Amazon ни идва на помощ! Услугата Snowmobile на Amazon ни позволява да качваме голямо количество данни в мобилно хранorще и след това да ги доставяме до желания address с камион! 
И така, имаме нов алгоритъм! „Ако искате да прехвърлите информация под формата на файлове на разстояние от 5000 мor и това ще отнеме повече от 14 дни за изпращане през интернет, трябва да изпратите данните на камион на Amazon.“ Тук произволно избрахме 14 дни. Да кажем, че това е най-дългият период, който можем да чакаме. Нека анализираме нашия алгоритъм. Какво ще кажете за скоростта му? Дори камионът да се движи само с 50 мor в час, той ще измине 5000 мor само за 100 часа. Това са малко повече от четири дни! Това е много по-добре от опцията за изпращане на данните през интернет. А Howво да кажем за сложността на този алгоритъм? Също така ли е линеен, т.е. O(n)? Не, не е. В края на краищата камионът не се интересува колко тежко го натоварвате — той все пак ще се движи с приблизително същата скорост и ще пристигне навреме. Независимо дали имаме 800 тераbyteа or 10 пъти повече, камионът все още ще стигне до местонаmeaningто си в рамките на 5 дни. С други думи, базираният на камион алгоритъм за пренос на данни има постоянна сложност. Тук "константа" означава, че не зависи от размера на входните данни. Поставете 1GB флашка в камиона, ще пристигне до 5 дни. Поставете в дискове, съдържащи 800 тераbyteа данни, те ще пристигнат в рамките на 5 дни. Когато се използва нотация с голямо O, постоянната сложност се означава с O(1) . Запознахме се с O(n) и O(1) , така че сега нека да разгледаме още примери в света на програмирането :) Да предположим, че ви е даден масив от 100 числа и задачата е да изведете всяко от тях на конзолата. Пишете обикновен 
В горния ред на изображението виждаме сортиран масив. Трябва да намерим числото 23 в него. Вместо да обикаляме числата, ние просто разделяме масива на 2 части и проверяваме средното число в масива. Намерете числото, което се намира в клетка 4 и го проверете (втори ред на изображението). Това число е 16, а ние търсим 23. Текущият брой е по-малък от това, което търсим. Какво означава това? Означава, чевсички предишни числа (тези, които се намират преди числото 16) не трябва да се проверяват : те гарантирано са по-малки от това, което търсим, защото нашият масив е сортиран! Продължаваме търсенето сред останалите 5 елемента. Забележка:направихме само едно сравнение, но вече сме елиминирали половината от възможните опции. Остават ни само 5 елемента. Ще повторим нашата предишна стъпка, като отново разделим оставащия подмасив наполовина и отново вземем средния елемент (3-тия ред в изображението). Числото е 56 и е по-голямо от това, което търсим. Какво означава това? Това означава, че сме елиминирали още 3 възможности: самото число 56, Howто и двете числа след него (тъй като те гарантирано са по-големи от 23, тъй като масивът е сортиран). Остават ни само 2 числа за проверка (последния ред в изображението) — числата с индекси на масива 5 и 6. Проверяваме първото от тях и намираме това, което търсихме — числото 23! Индексът му е 5! Нека да разгледаме резултатите от нашия алгоритъм и тогава ще ще анализира неговата сложност. Между другото, сега разбирате защо това се нарича двоично търсене: то разчита на многократно разделяне на данните наполовина. Резултатът е впечатляващ! Ако използвахме линейно търсене, за да търсим числото, ще ни трябват до 10 сравнения, но с двоично търсене изпълнихме задачата само с 3! В най-лошия случай ще има 4 сравнения (ако в последната стъпка числото, което искахме, беше второто от останалите възможности, а не първото. И така, Howво ще кажете за неговата сложност? Това е много интересен момент :) Алгоритъмът за двоично търсене е много по-малко зависим от броя на елементите в масива, отколкото алгоритъмът за линейно търсене (тоест проста итерация). С 10 елемента в масива линейното търсене ще се нуждае от максимум 10 сравнения, но двоичното търсене ще се нуждае от максимум 4 сравнения. Това е разлика с коефициент 2,5. Но за масив от 1000 елемента , линейното търсене ще се нуждае от до 1000 сравнения, но двоичното търсене ще изисква само 10 ! Разликата вече е 100 пъти! Забележка:броят на елементите в масива се е увеличил 100 пъти (от 10 на 1000), но броят на сравненията, необходими за двоично търсене, се е увеличил само с коефициент 2,5 (от 4 на 10). Ако стигнем до 10 000 елемента , разликата ще бъде още по-впечатляваща: 10 000 сравнения за линейно търсене и общо 14 сравнения за двоично търсене. И отново, ако броят на елементите се увеличи 1000 пъти (от 10 на 10 000), тогава броят на сравненията се увеличава само с коефициент 3,5 (от 4 на 14). Сложността на алгоритъма за двоично търсене е логаритмична or, ако използваме нотация голямо O, O(log n). Защо се казва така? Логаритъмът е като обратното на степенуването. Двоичният логаритъм е степента, на която трябва да се повдигне числото 2, за да се получи число. Например, имаме 10 000 елемента, които трябва да търсим с помощта на алгоритъма за двоично търсене. 
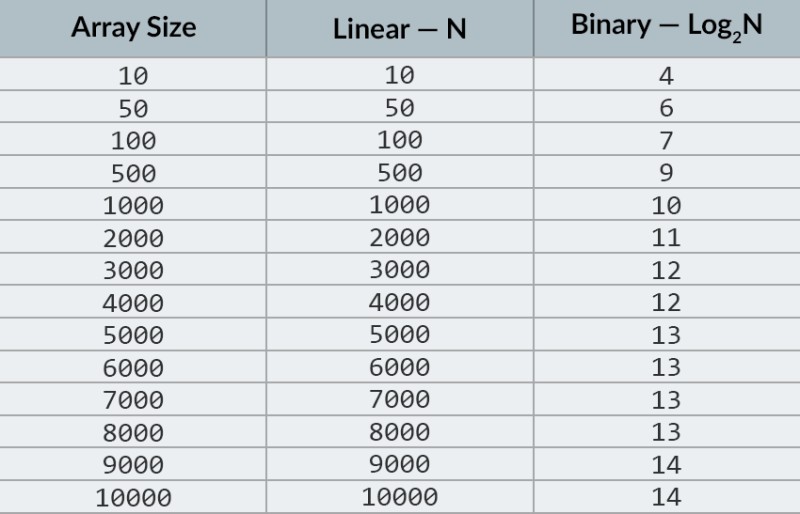В момента можете да погледнете tableта със стойности, за да знаете, че това ще изисква максимум 14 сравнения. Но Howво ще стане, ако никой не е предоставил такава table и трябва да изчислите точния максимален брой сравнения? Просто трябва да отговорите на един прост въпрос: на Howва степен трябва да повдигнете числото 2, така че резултатът да е по-голям or equals на броя на проверяваните елементи? За 10 000 това е 14-та степен. 2 на 13-та степен е твърде малко (8192), но 2 на 14-та степен = 16384, и това число удовлетворява нашето condition (то е по-голямо or равно на броя на елементите в масива). Намерихме логаритъма: 14. Ето от колко сравнения може да имаме нужда! :) Алгоритмите и алгоритмичната сложност е твърде обширна тема, за да се побере в един урок. Но да го знаете е много важно: много интервюта за работа ще включват въпроси, включващи алгоритми. За теория мога да ти препоръчам някои книги. Можете да започнете с " Алгоритми на Grokking ". Примерите в тази книга са написани на Python, но книгата използва много прост език и примери. Това е най-добрият вариант за начинаещ и освен това не е много голям. Сред по-сериозното четиво имаме книги на Робърт Лафор и Робърт Седжуик. И двете са написани на Java, което ще направи ученето малко по-лесно за вас. В крайна сметка вие сте добре запознати с този език! :) За ученици с добри математически умения най-добрият вариант е книгата на Томас Кормен . Но само теория няма да ви напълни корема! Знание! = Способност . Можете да практикувате решаване на проблеми, включващи алгоритми на HackerRank и LeetCode . Задачи от тези уебсайтове често се използват дори по време на интервюта в Google и Facebook, така че определено няма да ви е скучно :) За да затвърдите този материал от урока, ви препоръчвам да гледате това отлично видео за нотацията с голямо О в YouTube. Ще се видим в следващите уроци! :)
