Algoritmische complexiteit

Hoi! De les van vandaag zal iets anders zijn dan de rest. Het zal verschillen doordat het slechts indirect gerelateerd is aan Java. Dat gezegd hebbende, dit onderwerp is erg belangrijk voor elke programmeur. We gaan het hebben over algoritmen . Wat is een algoritme? In eenvoudige bewoordingen is het een reeks acties die moeten worden voltooid om een ​​gewenst resultaat te bereiken . We gebruiken algoritmen vaak in het dagelijks leven. Elke ochtend heb je bijvoorbeeld een specifieke taak: naar school of werk gaan, en tegelijkertijd zijn:

• Gekleed
• Schoon
• gevoed

Met welk algoritme kun je dit resultaat bereiken?

1. Wakker worden met een wekker.
2. Neem een ​​douche en was jezelf.
3. Maak ontbijt en wat koffie of thee.
4. Eten.
5. Als je je kleren de vorige avond niet hebt gestreken, strijk ze dan.
6. Aankleden.
7. Verlaat het huis.

Met deze reeks acties krijgt u zeker het gewenste resultaat. Bij het programmeren zijn we constant bezig om taken uit te voeren. Een aanzienlijk deel van deze taken kan worden uitgevoerd met behulp van al bekende algoritmen. Stel dat uw taak dit is: sorteer een lijst met 100 namen in een array . Deze taak is vrij eenvoudig, maar kan op verschillende manieren worden opgelost. Hier is een mogelijke oplossing: Algoritme voor het alfabetisch sorteren van namen:

1. Koop of download de editie uit 1961 van Webster's Third New International Dictionary.
2. Vind elke naam uit onze lijst in dit woordenboek.
3. Schrijf op een vel papier de pagina van het woordenboek waarop de naam staat.
4. Gebruik de stukjes papier om de namen te sorteren.

Zal een dergelijke opeenvolging van acties onze taak volbrengen? Ja, dat zal het zeker zijn. Is deze oplossing efficiënt ? Nauwelijks. Hier komen we bij een ander zeer belangrijk aspect van algoritmen: hun efficiëntie . Er zijn verschillende manieren om deze taak te volbrengen. Maar zowel bij het programmeren als in het gewone leven willen we de meest efficiënte manier kiezen. Als het jouw taak is om een ​​beboterd stuk toast te maken, kun je beginnen met het zaaien van tarwe en het melken van een koe. Maar dat zou inefficiënt zijnoplossing — het zal veel tijd kosten en veel geld kosten. U kunt uw eenvoudige taak volbrengen door simpelweg brood en boter te kopen. Hoewel je het probleem hiermee kunt oplossen, is het algoritme met tarwe en een koe te complex om in de praktijk te gebruiken. Bij het programmeren hebben we een speciale notatie, de grote O-notatie, om de complexiteit van algoritmen te beoordelen. Big O maakt het mogelijk om te beoordelen hoeveel de uitvoeringstijd van een algoritme afhangt van de grootte van de ingevoerde gegevens . Laten we eens kijken naar het eenvoudigste voorbeeld: gegevensoverdracht. Stel u voor dat u bepaalde informatie in de vorm van een bestand over een lange afstand (bijvoorbeeld 5000 mijl) moet verzenden. Welk algoritme zou het meest efficiënt zijn? Het hangt af van de gegevens waarmee u werkt. Stel dat we een audiobestand hebben van 10 MB. In dit geval is het meest efficiënte algoritme om het bestand via internet te verzenden. Het kon niet meer dan een paar minuten duren! Laten we ons algoritme herhalen: "Als u informatie in de vorm van bestanden over een afstand van 5000 mijl wilt overbrengen, moet u de gegevens via internet verzenden". Uitstekend. Laten we het nu analyseren. Vervult het onze taak?Nou ja, dat doet het wel. Maar wat kunnen we zeggen over de complexiteit ervan? Hmm, nu wordt het interessanter. Feit is dat ons algoritme erg afhankelijk is van de invoergegevens, namelijk de grootte van de bestanden. Als we 10 megabytes hebben, is alles in orde. Maar wat als we 500 megabytes moeten verzenden? 20 gigabyte? 500 terabyte? 30 petabyte? Zal ons algoritme stoppen met werken? Nee, al deze hoeveelheden gegevens kunnen inderdaad worden overgedragen. Duurt het langer? Ja het zal! Nu kennen we een belangrijk kenmerk van ons algoritme: hoe groter de hoeveelheid te verzenden gegevens, hoe langer het duurt om het algoritme uit te voeren. Maar we zouden graag een nauwkeuriger begrip willen hebben van deze relatie (tussen de grootte van de invoergegevens en de tijd die nodig is om deze te verzenden). In ons geval is de algoritmische complexiteit lineair . "Lineair" betekent dat naarmate de hoeveelheid invoergegevens toeneemt, de tijd die nodig is om deze te verzenden ongeveer evenredig toeneemt. Als de hoeveelheid gegevens verdubbelt, is de tijd die nodig is om ze te verzenden twee keer zo lang. Als de gegevens 10 keer toenemen, neemt de verzendtijd 10 keer toe. Met behulp van de grote O-notatie wordt de complexiteit van ons algoritme uitgedrukt als O(n). U moet deze notatie voor de toekomst onthouden - deze wordt altijd gebruikt voor algoritmen met lineaire complexiteit. Merk op dat we het niet hebben over verschillende dingen die hier kunnen variëren: internetsnelheid, de rekenkracht van onze computer, enzovoort. Bij het beoordelen van de complexiteit van een algoritme heeft het gewoon geen zin om rekening te houden met deze factoren — ze vallen in ieder geval buiten onze controle. Big O-notatie drukt de complexiteit van het algoritme zelf uit, niet de "omgeving" waarin het draait. Laten we doorgaan met ons voorbeeld. Stel dat we uiteindelijk ontdekken dat we bestanden van in totaal 800 terabytes moeten verzenden. We kunnen onze taak natuurlijk volbrengen door ze via internet te verzenden. Er is slechts één probleem: bij standaard datatransmissiesnelheden voor huishoudens (100 megabits per seconde) duurt het ongeveer 708 dagen. Bijna 2 jaar! :O Ons algoritme past hier duidelijk niet goed bij. We hebben een andere oplossing nodig! Onverwacht schiet IT-gigant Amazon ons te hulp! Met de Snowmobile-service van Amazon kunnen we een grote hoeveelheid gegevens uploaden naar mobiele opslag en deze vervolgens per vrachtwagen op het gewenste adres afleveren! We hebben dus een nieuw algoritme! "Als u informatie in de vorm van bestanden over een afstand van 5000 mijl wilt overbrengen en het verzenden via internet meer dan 14 dagen zou kosten, moet u de gegevens op een Amazon-vrachtwagen verzenden." We hebben hier willekeurig 14 dagen gekozen. Laten we zeggen dat dit de langste periode is die we kunnen wachten. Laten we ons algoritme analyseren. Hoe zit het met de snelheid? Zelfs als de truck slechts 50 mph rijdt, legt hij 5000 mijl af in slechts 100 uur. Dit is iets meer dan vier dagen! Dit is veel beter dan de mogelijkheid om de gegevens via internet te verzenden. En hoe zit het met de complexiteit van dit algoritme? Is het ook lineair, dus O(n)? Nee dat is het niet. Het maakt de truck immers niet uit hoe zwaar je hem laadt - hij rijdt nog steeds met ongeveer dezelfde snelheid en komt op tijd aan. Of we nu 800 terabyte hebben, of 10 keer zoveel, de truck is nog steeds binnen 5 dagen op zijn bestemming. Met andere woorden, het op vrachtwagens gebaseerde algoritme voor gegevensoverdracht heeft een constante complexiteit. Hier betekent "constant" dat het niet afhankelijk is van de invoergegevensgrootte. Stop een flashdrive van 1 GB in de vrachtwagen, deze komt binnen 5 dagen aan. Plaats schijven met 800 terabytes aan gegevens en deze komt binnen 5 dagen aan. Bij gebruik van de grote O-notatie wordt constante complexiteit aangeduid met O(1) . We zijn bekend geraakt met O(n) en O(1) , dus laten we nu eens kijken naar meer voorbeelden in de programmeerwereld :) Stel dat je een reeks van 100 getallen krijgt, en de taak is om ze allemaal weer te geven op de console. Je schrijft een gewone forlus die deze taak uitvoert

int[] numbers = new int[100];
// ...fill the array with numbers

for (int i: numbers) {
   System.out.println(i);
}

Wat is de complexiteit van dit algoritme? Lineair, dwz O(n). Het aantal acties dat het programma moet uitvoeren, hangt af van het aantal getallen dat eraan wordt doorgegeven. Als er 100 getallen in de array zijn, zijn er 100 acties (statements om strings op het scherm weer te geven). Als er 10.000 nummers in de array staan, moeten er 10.000 acties worden uitgevoerd. Kan ons algoritme op enigerlei wijze worden verbeterd? Nee. Wat er ook gebeurt, we zullen N door de array moeten laten gaan en N statements moeten uitvoeren om strings op de console weer te geven. Overweeg een ander voorbeeld.

public static void main(String[] args) {

   LinkedList<Integer> numbers = new LinkedList<>();
   numbers.add(0, 20202);
   numbers.add(0, 123);
   numbers.add(0, 8283);
}

We hebben een lege ruimte LinkedListwaarin we verschillende nummers invoegen. We moeten de algoritmische complexiteit evalueren van het invoegen van een enkel getal in LinkedListons voorbeeld, en hoe dit afhangt van het aantal elementen in de lijst. Het antwoord is O(1), dwz constante complexiteit . Waarom? Merk op dat we elk nummer aan het begin van de lijst invoegen. Bovendien zult u zich herinneren dat wanneer u een getal invoegt in een LinkedList, de elementen nergens heen bewegen. De links (of referenties) zijn bijgewerkt (als je bent vergeten hoe LinkedList werkt, bekijk dan een van onze oude lessen ). Als het eerste nummer in onze lijst is x, en we voegen het nummer y vooraan in de lijst in, dan hoeven we alleen maar dit te doen:

x.previous  = y;
y.previous = null;
y.next = x;

Wanneer we de links updaten, maakt het ons niet uit hoeveel nummers er al in de staanLinkedList , of het nu een of een miljard is. De complexiteit van het algoritme is constant, namelijk O(1).

Logaritmische complexiteit

Geen paniek! :) Als het woord 'logaritmisch' ervoor zorgt dat je deze les wilt afsluiten en wilt stoppen met lezen, wacht dan een paar minuten. Er zal hier geen gekke wiskunde zijn (er zijn tal van dergelijke verklaringen elders), en we zullen elk voorbeeld uit elkaar halen. Stel je voor dat het jouw taak is om één specifiek nummer te vinden in een reeks van 100 nummers. Meer precies, u moet controleren of het er is of niet. Zodra het vereiste nummer is gevonden, stopt het zoeken en geeft u het volgende weer in de console: "Het vereiste nummer is gevonden! Zijn index in de array = ...." Hoe zou u deze taak uitvoeren? Hier ligt de oplossing voor de hand: u moet de elementen van de array een voor een herhalen, beginnend bij de eerste (of bij de laatste) en controleren of het huidige nummer overeenkomt met het nummer dat u zoekt. Overeenkomstig, het aantal acties is rechtstreeks afhankelijk van het aantal elementen in de array. Als we 100 getallen hebben, moeten we mogelijk 100 keer naar het volgende element gaan en 100 vergelijkingen maken. Als er 1000 nummers zijn, dan kunnen er 1000 vergelijkingen zijn. Dit is duidelijk lineaire complexiteit, dwzO(n) . En nu voegen we een verfijning toe aan ons voorbeeld: de array waarin u het nummer moet vinden, is in oplopende volgorde gesorteerd . Verandert dit iets aan onze taak? We kunnen nog steeds bruut zoeken naar het gewenste nummer. Maar als alternatief zouden we het bekende binaire zoekalgoritme kunnen gebruiken .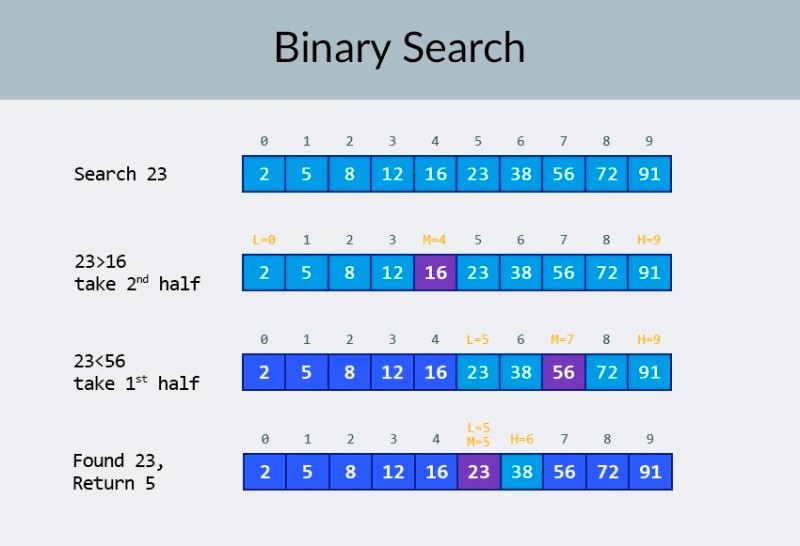 In de bovenste rij in de afbeelding zien we een gesorteerde array. We moeten het getal 23 erin vinden. In plaats van de getallen te herhalen, verdelen we de array eenvoudig in 2 delen en controleren we het middelste getal in de array. Zoek het nummer dat zich in cel 4 bevindt en vink het aan (tweede rij in de afbeelding). Dit aantal is 16 en we zoeken er 23. Het huidige aantal is lager dan wat we zoeken. Wat betekent dat? Het betekent datalle vorige nummers (die voor het nummer 16 liggen) hoeven niet te worden gecontroleerd : ze zijn gegarandeerd kleiner dan het nummer waarnaar we op zoek zijn, omdat onze reeks is gesorteerd! We gaan door met zoeken tussen de resterende 5 elementen. Opmerking:we hebben slechts één vergelijking uitgevoerd, maar we hebben al de helft van de mogelijke opties geëlimineerd. We hebben nog maar 5 elementen over. We herhalen onze vorige stap door de resterende subarray opnieuw in tweeën te delen en opnieuw het middelste element te nemen (de 3e rij in de afbeelding). Het nummer is 56, en het is groter dan degene die we zoeken. Wat betekent dat? Het betekent dat we nog eens 3 mogelijkheden hebben geëlimineerd: het getal 56 zelf en de twee getallen erachter (aangezien ze gegarandeerd groter zijn dan 23, omdat de array gesorteerd is). We hebben nog maar 2 getallen over om te controleren (de laatste rij in de afbeelding) — de getallen met matrixindices 5 en 6. We controleren de eerste en vinden wat we zochten — het getal 23! De index is 5! Laten we eens kijken naar de resultaten van ons algoritme, en dan gaan we Ik zal de complexiteit ervan analyseren. Trouwens, nu begrijp je waarom dit binair zoeken wordt genoemd: het is gebaseerd op het herhaaldelijk in tweeën delen van de gegevens. Het resultaat is indrukwekkend! Als we een lineaire zoekopdracht zouden gebruiken om naar het nummer te zoeken, zouden we tot 10 vergelijkingen nodig hebben, maar met een binaire zoekopdracht hebben we de taak volbracht met slechts 3! In het slechtste geval zouden er 4 vergelijkingen zijn (als in de laatste stap het nummer dat we wilden de tweede van de resterende mogelijkheden was, in plaats van de eerste. Dus hoe zit het met de complexiteit ervan? Dit is een heel interessant punt :) Het binaire zoekalgoritme is veel minder afhankelijk van het aantal elementen in de array dan het lineaire zoekalgoritme (dat wil zeggen eenvoudige iteratie). Met 10 elementen in de array heeft een lineaire zoekopdracht maximaal 10 vergelijkingen nodig, maar een binaire zoekopdracht heeft maximaal 4 vergelijkingen nodig. Dat is een verschil van een factor 2,5. Maar voor een reeks van 1000 elementen heeft een lineaire zoekopdracht tot 1000 vergelijkingen nodig, maar voor een binaire zoekopdracht zijn er slechts 10 nodig ! Het verschil is nu 100-voudig! Opmerking:het aantal elementen in de array is 100 keer toegenomen (van 10 naar 1000), maar het aantal vergelijkingen dat nodig is voor een binaire zoekopdracht is slechts met een factor 2,5 toegenomen (van 4 naar 10). Als we tot 10.000 elementen komen , zal het verschil nog indrukwekkender zijn: 10.000 vergelijkingen voor lineair zoeken en in totaal 14 vergelijkingen voor binair zoeken. En nogmaals, als het aantal elementen met 1000 keer toeneemt (van 10 naar 10000), dan neemt het aantal vergelijkingen toe met slechts een factor 3,5 (van 4 naar 14). De complexiteit van het binaire zoekalgoritme is logaritmisch , of, als we de grote O-notatie gebruiken, O(log n). Waarom heet het zo? De logaritme is als het tegenovergestelde van machtsverheffen. De binaire logaritme is de macht waartoe het getal 2 moet worden verhoogd om een ​​getal te verkrijgen. We hebben bijvoorbeeld 10.000 elementen die we nodig hebben om te zoeken met behulp van het binaire zoekalgoritme. 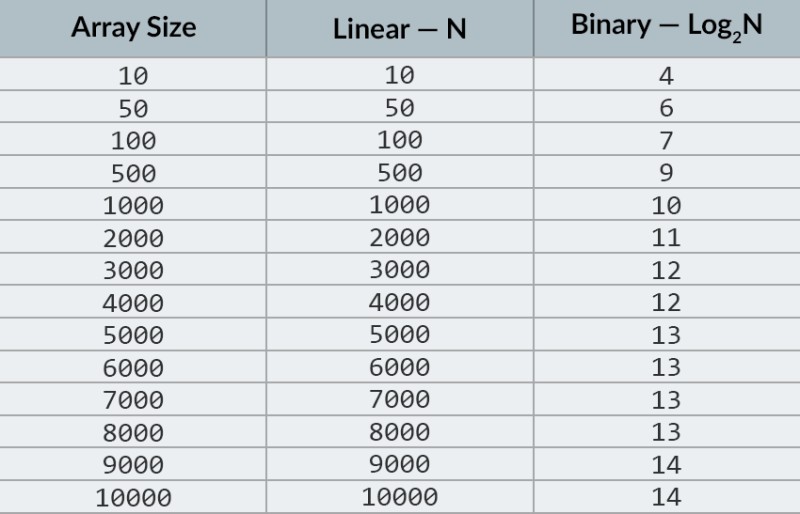Momenteel kunt u de tabel met waarden bekijken om te weten dat hiervoor maximaal 14 vergelijkingen nodig zijn. Maar wat als niemand zo'n tabel heeft verstrekt en u het exacte maximale aantal vergelijkingen moet berekenen? U hoeft alleen maar een simpele vraag te beantwoorden: tot welke macht moet u het getal 2 verhogen zodat het resultaat groter is dan of gelijk is aan het aantal te controleren elementen? Voor 10.000 is het de 14e macht. 2 tot de 13e macht is te klein (8192), maar 2 tot de 14e macht = 16384, en dit aantal voldoet aan onze voorwaarde (het is groter dan of gelijk aan het aantal elementen in de array). We hebben de logaritme gevonden: 14. Zoveel vergelijkingen hebben we misschien nodig! :) Algoritmen en algoritmische complexiteit is een te breed onderwerp om in één les te passen. Maar het weten is heel belangrijk: veel sollicitatiegesprekken bevatten vragen met algoritmen. Voor de theorie kan ik je enkele boeken aanraden. U kunt beginnen met " Grokking-algoritmen ". De voorbeelden in dit boek zijn geschreven in Python, maar het boek gebruikt zeer eenvoudige taal en voorbeelden. Het is de beste optie voor een beginner en bovendien is het niet erg groot. Onder meer serieuze lectuur hebben we boeken van Robert Lafore en Robert Sedgewick. Beide zijn geschreven in Java, wat het leren een beetje makkelijker voor je maakt. U kent deze taal immers goed! :) Voor studenten met goede wiskundige vaardigheden is de beste optie het boek van Thomas Cormen . Maar theorie alleen zal je buik niet vullen! Kennis != Vermogen . U kunt oefenen met het oplossen van problemen met algoritmen op HackerRank en LeetCode . Taken van deze websites worden vaak gebruikt, zelfs tijdens interviews bij Google en Facebook, dus je zult je zeker niet vervelen :) Om dit lesmateriaal te versterken, raad ik je aan om deze uitstekende video over grote O-notatie op YouTube te bekijken. Tot ziens in de volgende lessen! :)