Buborékos Java

Ha valaha is hallottál a programozás rendezési módszereiről, valószínűleg ez a buborékos rendezési algoritmus volt. Ez egy híres. Minden programozó nem azért ismeri a buborékos rendezést (vagy legalábbis hallott róla tanulás közben), mert ez a világ legjobb rendezési algoritmusa, hanem a legegyszerűbb. Ezt az algoritmust általában tanulási célokra használják, vagy feladatként megkaphatja a Java Junior Interview-ban. A Java Bubble rendezési algoritmus nagyon könnyen érthető, de nem hatékony. Na mindegy, találjuk ki.

Mi a válogatás

Először is meg kell értened, hogy mi a rendezés általában, és mit tudunk rendezni a Java programokban. Ha két vagy több elemet vagy objektumot össze tudunk hasonlítani bármely attribútumuk alapján, az azt jelenti, hogy ezek az attribútumok szerint rendezhetők. Például számok növekvő vagy csökkenő sorrendben vagy szavak ábécé sorrendben. Ezért az elemeknek összehasonlíthatónak kell lenniük egymással. Egyébként minek az elemei? Java nyelven összehasonlíthatjuk a Collections elemeit. Például rendezhetjük az egész számok, karakterláncok és így tovább az Array vagy ArrayList listát.

Hogyan működik a buborékos rendezés

Tegyük fel, hogy az egész számok tömbjét növekvő sorrendbe kell rendeznünk, azaz a legkisebbtől a legnagyobbig. Először végigmegyünk a teljes tömbön, és minden 2 szomszédos elemet összehasonlítunk. Ha rossz sorrendben vannak (a bal oldali szomszéd nagyobb, mint a jobb), kicseréljük őket. Az első lépésnél a végén a legnagyobb elem jelenik meg (ha növekvő sorrendben rendezzük). Mondhatni, a legnagyobb elem „felbukkan”. Ez az oka a Buborék rendezési algoritmus nevének. Az első lépést megismételjük az elsőtől az utolsó előtti elemig. Megvan a második legnagyobb elem az utolsó előtti helyen. Stb. Kicsit javíthatunk az algoritmuson, ha megnézzük, hogy az előző lépésben történt-e legalább egy csere. Ha nem, akkor leállítjuk a tömbben való futást.

Buborék rendezési példa

Rendezzük az egész számok tömbjét, azt az egyet, amelyet lent egy képen láthat. 1. lépés: végigmegyünk a tömbön. Az algoritmus az első két elemmel (0 és 1 indexű), a 8-mal és a 7-tel indul, és ellenőrzi, hogy a helyes sorrendben vannak-e. Nyilván 8 > 7, ezért cseréljük őket. Ezután a második és harmadik elemet nézzük (1. és 2. index), most ezek a 8 és 1. Ugyanezen okokból felcseréljük őket. Harmadszorra 8-at és 2-t, illetve legalább 8-at és 5-öt hasonlítunk össze. Összesen négy cserét hajtottunk végre: (8, 7), (8, 1), (8, 2) és (8, 5). Egy 8-as érték, a legnagyobb ebben a tömbben, felbukkant a lista végén a megfelelő helyre. 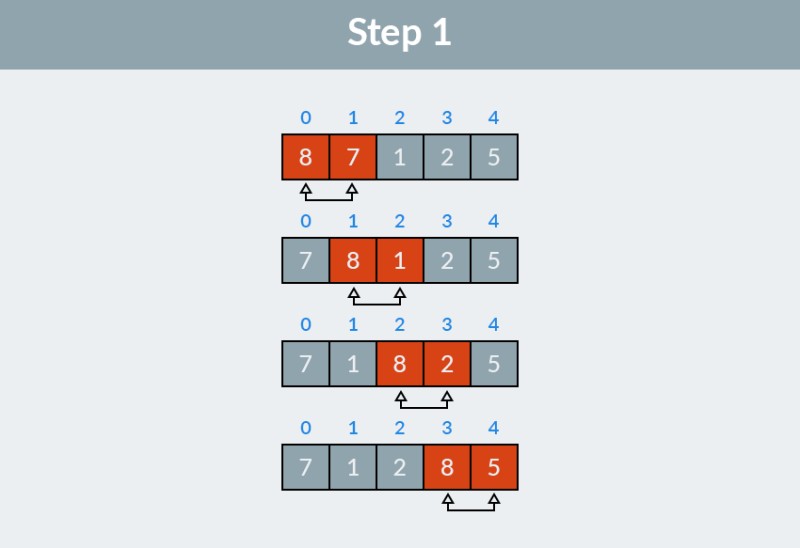A buborékos rendezési algoritmus első lépésének eredménye a következő tömb: 2. lépés. Ugyanezt tegye a (7,1), (7,2) és (7,5) pontokkal. A 7-es most az utolsó előtti helyen áll, és nem kell összehasonlítani a lista "farkával", már rendezve van. A buborékos rendezési algoritmus második lépésének eredménye a következő tömb: Mint láthatja, ez a tömb már rendezve van. Mindenesetre a Bubble Sort algoritmusnak legalább még egyszer működnie kell. 3. lépés. Még egyszer végigmegyünk a tömbön. Itt nincs mit cserélni, tehát ha „továbbfejlesztett” Bubble Sort algoritmust használunk (ellenőrizve, hogy az előző lépésben történt-e legalább egy csere), akkor ez a lépés az utolsó.

Buborékos rendezési Java kód

Buborékos rendezés Java megvalósítás

Hozzunk létre két módszert a buborékos rendezéshez. Az első, a bubbleSort(int[] myArray) egy sík. Minden alkalommal végigfut a tömbön. A második, az optimizedBubbleSort(int myArray[]) az algoritmus leállításával van optimalizálva, ha a belső hurok nem okozott cserét. A számláló megmutatja, hány lépést tett meg a válogatás során. Itt van egy Bubble sort Java megvalósítás:

import java.util.Arrays;

public class BubbleSortExample {

   //  Plane Bubble sort example

   public static int[] bubbleSort(int[] myArray) {

       int temp = 0;  //  temporary element for swapping
       int counter = 0;  //  element to count quantity of steps

       for (int i = 0; i < myArray.length; i++) {
           counter = i + 1;
           for (int j = 1; j < (myArray.length - i); j++) {

               if (myArray[j - 1] > myArray[j]) {
                   //  swap array’s elements using temporary element
                   temp = myArray[j - 1];
                   myArray[j - 1] = myArray[j];
                   myArray[j] = temp;
               }
           }
       }
       System.out.println("Steps quantity, non optimized = " + counter);
       return myArray;
   }
   //  An optimized version of Java Bubble Sorting

   static int[] optimizedBubbleSort(int myArray[]) {
       int temp;
       boolean swapped;
       int counter = 0;  //  element to count quantity of steps
       for (int i = 0; i < myArray.length - 1; i++) {
           counter = i + 1;
           swapped = false;
           for (int j = 0; j < myArray.length - i - 1; j++) {
               //  counter++;
               if (myArray[j] > myArray[j + 1]) {
                   //  swap arr[j] and arr[j+1]
                   temp = myArray[j];
                   myArray[j] = myArray[j + 1];
                   myArray[j + 1] = temp;
                   swapped = true;

               }
           }  //  counter = i;
           //  If there weren't elements to swap in inner loop, then break
           if (swapped == false) {

               break;

           }
       }
       System.out.println("steps quantity, optimized = " + counter);
       return myArray;
   }


   public static void main(String[] args) {
       int arr[] = {8, 7, 1, 2, 5};
       int arr1[] = {8, 7, 1, 2, 5};

       System.out.println("Array arr Before Bubble Sort");
       //  we use java.util.Arrays toString method to print the array  
 System.out.println(Arrays.toString(arr));

       System.out.println("Array arr After Bubble Sort");
       System.out.println(Arrays.toString(bubbleSort(arr)));

       System.out.println("Array arr1 Before Bubble Sort");
       System.out.println(Arrays.toString(arr1));

       System.out.println("Array arr1 After Optimized Bubble Sort");
       System.out.println(Arrays.toString(optimizedBubbleSort(arr1)));
   }
}

A Bubble sort Java algoritmus munkájának eredménye:

Array arr Before Bubble Sort
[8, 7, 1, 2, 5]
Array arr After Bubble Sort
Steps quantity, non optimized = 5
[1, 2, 5, 7, 8]
Array arr1 Before Bubble Sort
[8, 7, 1, 2, 5]
Array arr1 After Optimized Bubble Sort
steps quantity, optimized = 3
[1, 2, 5, 7, 8]

Mennyire hatékony a buborékos rendezés?

A buborékrendezés az egyik legkönnyebben megvalósítható algoritmus, de nem hatékony. Egy pár egymásba ágyazott hurkot igényel. Még az algoritmus optimalizált változatában is a legrosszabb esetben (az adathalmaz minden eleme fordított sorrendben van a kívánthoz képest) a külső ciklus az adathalmaz n elemére egyszer ismétlődik. A belső ciklus az első alkalommal n- szer, a második alkalommal ( n-1 ) ismétlődik , és így tovább. Ezért az összes n elem rendezéséhez a ciklusokat n*(n-1)/2 alkalommal kell végrehajtani . O (n ² )időbonyolultság, és azt jelenti, hogy az algoritmus körülbelül 500 000 összehasonlítást végez egy tömb 1000 eleméhez. A buborékos rendezési algoritmus azonban meglehetősen hatékony a memóriahasználatban (a memória összetettsége O(n) ), és nagyon jó a majdnem rendezett kis adatkészletekhez.