バブルソートJava

プログラミングにおけるソート方法について聞いたことがあるなら、それはおそらくバブル ソート アルゴリズムだったでしょう。有名なものです。すべてのプログラマがバブル ソートを知っている (または少なくとも学習中に聞いたことがある) のは、それが世界で最高のソート アルゴリズムだからではなく、最も簡単なアルゴリズムだからです。このアルゴリズムは通常、学習目的で使用されるか、Java ジュニアの面接のタスクとして提供される場合があります。Java バブル ソート アルゴリズムは非常に理解しやすいですが、効率的なアルゴリズムではありません。とにかく、それを理解しましょう。

並べ替えとは

まず、ソートとは一般的に何なのか、そして Java プログラムで何をソートできるのかを理解する必要があります。2 つ以上の要素またはオブジェクトをそれらの属性のいずれかで比較できる場合は、その属性でそれらを並べ替えることができることを意味します。たとえば、数字を昇順または降順に並べたり、単語をアルファベット順に並べたりします。したがって、要素は互いに比較できる必要があります。ちなみに要素は何でしょうか？Java では、コレクションの要素を比較できます。たとえば、整数、文字列などの Array または ArrayList を並べ替えることができます。

バブルソートの仕組み

たとえば、整数の配列を昇順、つまり最小値から最大値の順に並べ替える必要があるとします。まず、配列全体に沿って、隣接する 2 つの要素ごとに比較します。それらの順序が間違っている場合 (左隣のものが右のものより大きい場合)、それらを交換します。最後の最初のパスでは、最大の要素が表示されます (昇順でソートした場合)。最大の要素は「現れる」と言えるかもしれません。それがバブル ソート アルゴリズムの名前の理由です。最初のステップを最初の要素から最後から 2 番目の要素まで繰り返します。最後から 2 番目の場所に 2 番目に大きな要素があります。等々。前のステップで少なくとも 1 つの交換が行われたかどうかをチェックすることで、アルゴリズムを少し改善できます。そうでない場合は、アレイに沿った走行を中止します。

バブルソートの例

整数の配列を並べ替えてみましょう。下の図に示されているものです。 ステップ 1: 配列を調べます。アルゴリズムは、最初の 2 つの要素 (インデックス 0 と 1)、8 と 7 から始まり、それらが正しい順序であるかどうかを確認します。明らかに 8 > 7 なので、それらを交換します。次に、2 番目と 3 番目の要素 (インデックス 1 と 2) に注目します。現在、これらは 8 と 1 です。同じ理由で、これらを交換します。3 回目では、8 と 2、そして少なくとも 8 と 5 を比較します。合計 4 つの交換を行いました: (8, 7)、(8, 1)、(8, 2)、および (8, 5)。この配列内で最大の値 8 が、リストの末尾の正しい位置にポップアップ表示されます。 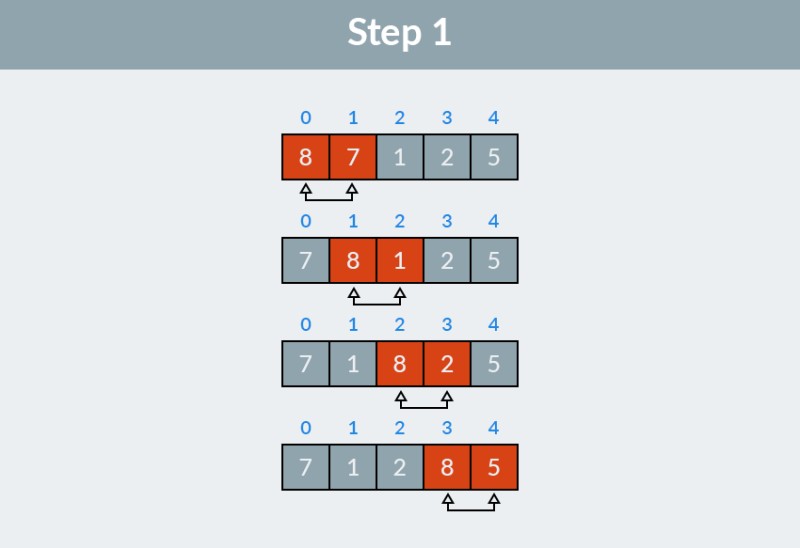バブル ソート アルゴリズムの最初のステップが動作した結果は、次の配列になります。 ステップ 2. (7,1)、(7,2)、および (7,5) についても同じことを行います。7 は最後から 2 番目の位置にあり、リストの「末尾」と比較する必要はありません。すでにソートされています。 バブル ソート アルゴリズムの 2 番目のステップの結果は、次の配列になります。 ご覧のとおり、この配列はすでにソートされています。とにかく、バブルソートアルゴリズムを少なくとももう一度実行する必要があります。ステップ3. 配列をもう一度調べます。ここでは交換するものがないため、「改良された」バブル ソート アルゴリズム (前のステップで少なくとも 1 つの交換が行われたかどうかをチェックする) を使用している場合、このステップが最後のステップになります。

バブルソート Java コード

バブルソート Java の実現

バブルソート用の 2 つのメソッドを作成しましょう。最初のもの、bubbleSort(int[] myArray) は平面のものです。毎回配列を介して実行されます。2 番目の最適化 BubbleSort(int myArray[]) は、内部ループでスワップが発生しなかった場合にアルゴリズムを停止することで最適化されます。カウンターは、並べ替え中に実行したステップ数を示します。ここにバブル ソート Java の実現があります。

import java.util.Arrays;

public class BubbleSortExample {

   //  Plane Bubble sort example

   public static int[] bubbleSort(int[] myArray) {

       int temp = 0;  //  temporary element for swapping
       int counter = 0;  //  element to count quantity of steps

       for (int i = 0; i < myArray.length; i++) {
           counter = i + 1;
           for (int j = 1; j < (myArray.length - i); j++) {

               if (myArray[j - 1] > myArray[j]) {
                   //  swap array’s elements using temporary element
                   temp = myArray[j - 1];
                   myArray[j - 1] = myArray[j];
                   myArray[j] = temp;
               }
           }
       }
       System.out.println("Steps quantity, non optimized = " + counter);
       return myArray;
   }
   //  An optimized version of Java Bubble Sorting

   static int[] optimizedBubbleSort(int myArray[]) {
       int temp;
       boolean swapped;
       int counter = 0;  //  element to count quantity of steps
       for (int i = 0; i < myArray.length - 1; i++) {
           counter = i + 1;
           swapped = false;
           for (int j = 0; j < myArray.length - i - 1; j++) {
               //  counter++;
               if (myArray[j] > myArray[j + 1]) {
                   //  swap arr[j] and arr[j+1]
                   temp = myArray[j];
                   myArray[j] = myArray[j + 1];
                   myArray[j + 1] = temp;
                   swapped = true;

               }
           }  //  counter = i;
           //  If there weren't elements to swap in inner loop, then break
           if (swapped == false) {

               break;

           }
       }
       System.out.println("steps quantity, optimized = " + counter);
       return myArray;
   }


   public static void main(String[] args) {
       int arr[] = {8, 7, 1, 2, 5};
       int arr1[] = {8, 7, 1, 2, 5};

       System.out.println("Array arr Before Bubble Sort");
       //  we use java.util.Arrays toString method to print the array  
 System.out.println(Arrays.toString(arr));

       System.out.println("Array arr After Bubble Sort");
       System.out.println(Arrays.toString(bubbleSort(arr)));

       System.out.println("Array arr1 Before Bubble Sort");
       System.out.println(Arrays.toString(arr1));

       System.out.println("Array arr1 After Optimized Bubble Sort");
       System.out.println(Arrays.toString(optimizedBubbleSort(arr1)));
   }
}

バブルソート Java アルゴリズムの結果:

Array arr Before Bubble Sort
[8, 7, 1, 2, 5]
Array arr After Bubble Sort
Steps quantity, non optimized = 5
[1, 2, 5, 7, 8]
Array arr1 Before Bubble Sort
[8, 7, 1, 2, 5]
Array arr1 After Optimized Bubble Sort
steps quantity, optimized = 3
[1, 2, 5, 7, 8]

バブルソートはどのくらい効率的ですか?

バブル ソートは実装が最も簡単なアルゴリズムの 1 つですが、効率的ではありません。ネストされたループのペアが必要です。最悪の場合 (データ セットの各要素が目的の要素と逆の順序になっている) のアルゴリズムの最適化バージョンでも、外側のループはデータ セットのn要素ごとに 1 回反復されます。内側のループは、最初はn回、 2 回目は( n-1 ) 回、というように繰り返します。したがって、すべてのn要素をソートするには、ループをn*(n-1)/2回実行する必要があります。O(n ² )を呼び出します。時間計算量とは、アルゴリズムが配列の 1000 個の要素に対して約 500,000 回の比較を行うことを意味します。ただし、バブル ソート アルゴリズムはメモリ使用量に関しては非常に効果的であり (メモリの複雑さはO(n) )、ほとんどソートされた小さなデータセットには非常に適しています。