冒泡排序Java

如果您聽說過編程中的排序方法，很可能是冒泡排序算法。這是一個著名的。每個程序員都知道冒泡排序（或者至少在學習時聽說過）並不是因為它是世界上最好的排序算法，而是因為它是最簡單的算法。該算法通常用於學習目的，或者您可以在 Java 初級面試中將其作為一項任務。Java 冒泡排序算法很容易理解，但是它不是一個高效的算法。無論如何，讓我們弄清楚。

什麼是排序

首先，你需要明白排序一般是什麼，我們在Java程序中可以排序什麼。如果我們可以通過它們的任何屬性比較兩個或多個元素或對象，則意味著它們可以按該屬性進行排序。例如，按升序或降序排列的數字或按字母順序排列的單詞。因此，元素必須相互比較。順便問一下，什麼元素？在Java中，我們可以比較Collections的元素。例如，我們可以對整數、字符串等的 Array 或 ArrayList 進行排序。

冒泡排序是如何工作的

比方說，我們需要對一個整數數組進行升序排序，即從小到大。首先，我們遍歷整個數組並比較每 2 個相鄰元素。如果它們的順序錯誤（左邊的鄰居比右邊的大），我們交換它們。在最後的第一次傳遞中，它會出現最大的元素（如果我們按升序排序）。你可能會說，最大的元素“彈出”。這就是冒泡排序算法名稱的原因。我們從第一個元素到倒數第二個元素重複第一步。我們在倒數第二個位置找到了第二大元素。等等。我們可以通過檢查上一步是否至少進行了一次交換來稍微改進算法。如果不是，我們將停止沿著陣列運行。

冒泡排序示例

讓我們對整數數組進行排序，您可能會在下面的圖片中看到它。 第 1 步：我們正在遍歷數組。該算法從前兩個元素（索引為 0 和 1）、8 和 7 開始，並檢查它們的順序是否正確。顯然，8 > 7，所以我們交換它們。接下來，我們查看第二個和第三個元素（索引 1 和 2），現在它們是 8 和 1。出於同樣的原因，我們交換它們。我們第三次比較 8 和 2，至少比較 8 和 5。我們總共進行了四次交換：(8, 7)、(8, 1)、(8, 2) 和 (8, 5)。值 8，此數組中最大的值，在列表末尾彈出到正確位置。 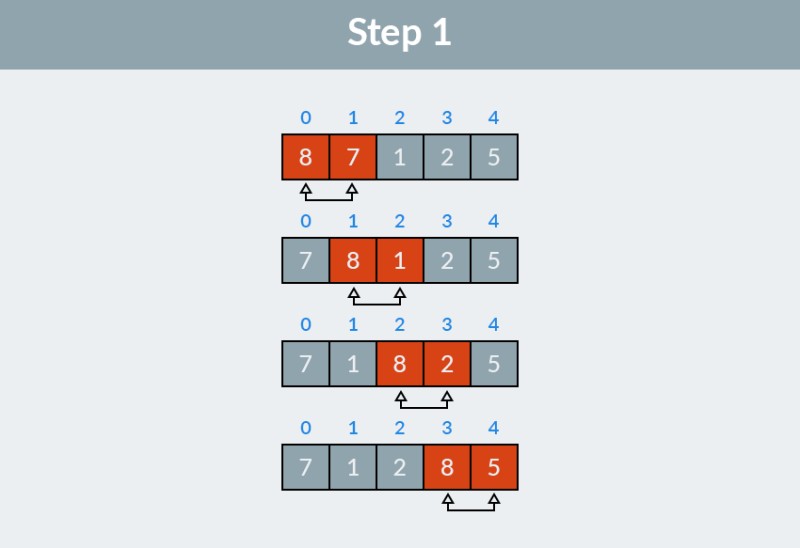冒泡排序算法第一步工作的結果是下一個數組： 第 2 步。對 (7,1)、(7,2) 和 (7,5) 執行相同的操作。7 現在處於倒數第二的位置，我們不需要將它與列表的“尾巴”進行比較，它已經排好序了。 冒泡排序算法第二步運行的結果是下一個數組： 如您所見，該數組已經排序。無論如何，冒泡排序算法應該至少再運行一次。第三步。我們再次遍歷數組。這裡沒有什麼可交換的，所以如果我們使用“改進的”冒泡排序算法（檢查上一步是否至少進行了一次交換），這一步就是最後一步。

冒泡排序Java代碼

冒泡排序Java實現

讓我們為冒泡排序創建兩個方法。第一個，bubbleSort(int[] myArray)是平面的。它每次都遍歷數組。第二個，optimizedBubbleSort(int myArray[])通過在內部循環沒有引起任何交換的情況下停止算法來優化。計數器顯示您在排序時執行了多少步。這裡我們有冒泡排序 Java 實現：

import java.util.Arrays;

public class BubbleSortExample {

   //  Plane Bubble sort example

   public static int[] bubbleSort(int[] myArray) {

       int temp = 0;  //  temporary element for swapping
       int counter = 0;  //  element to count quantity of steps

       for (int i = 0; i < myArray.length; i++) {
           counter = i + 1;
           for (int j = 1; j < (myArray.length - i); j++) {

               if (myArray[j - 1] > myArray[j]) {
                   //  swap array’s elements using temporary element
                   temp = myArray[j - 1];
                   myArray[j - 1] = myArray[j];
                   myArray[j] = temp;
               }
           }
       }
       System.out.println("Steps quantity, non optimized = " + counter);
       return myArray;
   }
   //  An optimized version of Java Bubble Sorting

   static int[] optimizedBubbleSort(int myArray[]) {
       int temp;
       boolean swapped;
       int counter = 0;  //  element to count quantity of steps
       for (int i = 0; i < myArray.length - 1; i++) {
           counter = i + 1;
           swapped = false;
           for (int j = 0; j < myArray.length - i - 1; j++) {
               //  counter++;
               if (myArray[j] > myArray[j + 1]) {
                   //  swap arr[j] and arr[j+1]
                   temp = myArray[j];
                   myArray[j] = myArray[j + 1];
                   myArray[j + 1] = temp;
                   swapped = true;

               }
           }  //  counter = i;
           //  If there weren't elements to swap in inner loop, then break
           if (swapped == false) {

               break;

           }
       }
       System.out.println("steps quantity, optimized = " + counter);
       return myArray;
   }


   public static void main(String[] args) {
       int arr[] = {8, 7, 1, 2, 5};
       int arr1[] = {8, 7, 1, 2, 5};

       System.out.println("Array arr Before Bubble Sort");
       //  we use java.util.Arrays toString method to print the array  
 System.out.println(Arrays.toString(arr));

       System.out.println("Array arr After Bubble Sort");
       System.out.println(Arrays.toString(bubbleSort(arr)));

       System.out.println("Array arr1 Before Bubble Sort");
       System.out.println(Arrays.toString(arr1));

       System.out.println("Array arr1 After Optimized Bubble Sort");
       System.out.println(Arrays.toString(optimizedBubbleSort(arr1)));
   }
}

冒泡排序Java算法工作的結果：

Array arr Before Bubble Sort
[8, 7, 1, 2, 5]
Array arr After Bubble Sort
Steps quantity, non optimized = 5
[1, 2, 5, 7, 8]
Array arr1 Before Bubble Sort
[8, 7, 1, 2, 5]
Array arr1 After Optimized Bubble Sort
steps quantity, optimized = 3
[1, 2, 5, 7, 8]

冒泡排序的效率如何？

冒泡排序是最容易實現的算法之一，但效率不高。它需要一對嵌套循環。即使在最壞情況下（數據集的每個元素與所需元素的順序相反）的優化版本的算法中，外循環也會為數據集的 n 個元素中的每一個元素迭代一次。內部循環第一次迭代n次，第二次迭代 ( n-1 )，依此類推。因此，要對所有n元素進行排序，需要執行循環n*(n-1)/2次。它調用O(n ² )時間複雜度，意味著該算法對數組的 1000 個元素進行大約 500 000 次比較。然而，冒泡排序算法在內存使用方面非常有效（內存複雜度為O(n)）並且對於幾乎已排序的小型數據集非常有用。