Als je ooit hebt gehoord van sorteermethoden bij het programmeren, was dit hoogstwaarschijnlijk het algoritme voor het sorteren van bellen. Het is een bekende. Elke programmeur kent bubbelsortering (of heeft er in ieder geval van gehoord tijdens het leren), niet omdat het het beste sorteeralgoritme ter wereld is, maar het gemakkelijkste. Dit algoritme wordt meestal gebruikt voor leerdoeleinden of u kunt het als taak krijgen in uw Java Junior Interview. Het Java Bubble-sorteeralgoritme is heel gemakkelijk te begrijpen, maar het is niet efficiënt. Hoe dan ook, laten we het uitzoeken.
![Bellen sorteren - 2]() Stap 1: we gaan door de array. Het algoritme begint met de eerste twee elementen (met indices 0 en 1), 8 en 7, en controleert of ze in de juiste volgorde staan. Het is duidelijk dat 8 > 7, dus we wisselen ze om. Vervolgens kijken we naar het tweede en derde element (indices 1 en 2), nu zijn dit 8 en 1. Om dezelfde redenen wisselen we ze om. Voor de derde keer vergelijken we 8 en 2 en in ieder geval 8 en 5. We hebben in totaal vier uitwisselingen gedaan: (8, 7), (8, 1), (8, 2) en (8, 5). Een waarde van 8, de grootste in deze array, verscheen aan het einde van de lijst op de juiste positie.
Stap 1: we gaan door de array. Het algoritme begint met de eerste twee elementen (met indices 0 en 1), 8 en 7, en controleert of ze in de juiste volgorde staan. Het is duidelijk dat 8 > 7, dus we wisselen ze om. Vervolgens kijken we naar het tweede en derde element (indices 1 en 2), nu zijn dit 8 en 1. Om dezelfde redenen wisselen we ze om. Voor de derde keer vergelijken we 8 en 2 en in ieder geval 8 en 5. We hebben in totaal vier uitwisselingen gedaan: (8, 7), (8, 1), (8, 2) en (8, 5). Een waarde van 8, de grootste in deze array, verscheen aan het einde van de lijst op de juiste positie. ![Bellen sorteren - 3]() Het resultaat van de eerste stap van het Bubble sort-algoritme is de volgende array:
Het resultaat van de eerste stap van het Bubble sort-algoritme is de volgende array: ![Bellen sorteren - 4]() Stap 2. Doe hetzelfde met (7,1), (7,2) en (7,5). 7 staat nu op de voorlaatste plaats en we hoeven het niet te vergelijken met de "staart" van de lijst, het is al gesorteerd.
Stap 2. Doe hetzelfde met (7,1), (7,2) en (7,5). 7 staat nu op de voorlaatste plaats en we hoeven het niet te vergelijken met de "staart" van de lijst, het is al gesorteerd. ![Bellen sorteren - 5]() Het resultaat van de tweede stap van het Bubble sort-algoritme is de volgende array:
Het resultaat van de tweede stap van het Bubble sort-algoritme is de volgende array: ![Bellen sorteren - 6]() Zoals u kunt zien, is deze array al gesorteerd. Hoe dan ook, het Bubble Sort-algoritme zou nog minstens één keer aan de slag moeten gaan. Stap 3. We gaan nog een keer door de array. Niets om hier te ruilen, dus als we het "verbeterde" Bubble Sort-algoritme gebruiken (met controle of er ten minste één uitwisseling bij de vorige stap is gemaakt), is deze stap de laatste.
Zoals u kunt zien, is deze array al gesorteerd. Hoe dan ook, het Bubble Sort-algoritme zou nog minstens één keer aan de slag moeten gaan. Stap 3. We gaan nog een keer door de array. Niets om hier te ruilen, dus als we het "verbeterde" Bubble Sort-algoritme gebruiken (met controle of er ten minste één uitwisseling bij de vorige stap is gemaakt), is deze stap de laatste.
Wat is sorteren
Allereerst moet u begrijpen wat sorteren in het algemeen is en wat we kunnen sorteren in Java-programma's. Als we twee of meer elementen of objecten kunnen vergelijken op basis van een van hun attributen, betekent dit dat ze op dit attribuut kunnen worden gesorteerd. Bijvoorbeeld getallen in oplopende of aflopende volgorde of woorden alfabetisch. De elementen moeten dus met elkaar vergelijkbaar zijn. Trouwens, de elementen van wat? In Java kunnen we de elementen van Collecties vergelijken. We kunnen bijvoorbeeld Array of ArrayList van integers, Strings enzovoort sorteren.Hoe werkt bubbelsortering?
Laten we zeggen dat we een reeks gehele getallen in oplopende volgorde moeten sorteren, dat wil zeggen van het kleinste naar het grootste getal. Eerst gaan we langs de hele reeks en vergelijken we elke 2 aangrenzende elementen. Als ze in de verkeerde volgorde staan (de linkerbuur is groter dan de rechter), wisselen we ze om. Bij de eerste doorgang aan het einde zal het grootste element verschijnen (als we in oplopende volgorde sorteren). Je zou kunnen zeggen dat het grootste element "opduikt". Dat is de reden van de algoritmenaam Bubble sort. We herhalen de eerste stap van het eerste tot het voorlaatste element. We hebben het op een na grootste element op de voorlaatste plaats. Enzovoort. We kunnen een algoritme een klein beetje verbeteren door na te gaan of er ten minste één uitwisseling bij de vorige stap is gemaakt. Als dat niet het geval is, stoppen we met rennen langs de reeks.Bubble sort voorbeeld
Laten we de reeks gehele getallen sorteren, de ene die u hieronder op een afbeelding kunt zien. Stap 1: we gaan door de array. Het algoritme begint met de eerste twee elementen (met indices 0 en 1), 8 en 7, en controleert of ze in de juiste volgorde staan. Het is duidelijk dat 8 > 7, dus we wisselen ze om. Vervolgens kijken we naar het tweede en derde element (indices 1 en 2), nu zijn dit 8 en 1. Om dezelfde redenen wisselen we ze om. Voor de derde keer vergelijken we 8 en 2 en in ieder geval 8 en 5. We hebben in totaal vier uitwisselingen gedaan: (8, 7), (8, 1), (8, 2) en (8, 5). Een waarde van 8, de grootste in deze array, verscheen aan het einde van de lijst op de juiste positie.
Stap 1: we gaan door de array. Het algoritme begint met de eerste twee elementen (met indices 0 en 1), 8 en 7, en controleert of ze in de juiste volgorde staan. Het is duidelijk dat 8 > 7, dus we wisselen ze om. Vervolgens kijken we naar het tweede en derde element (indices 1 en 2), nu zijn dit 8 en 1. Om dezelfde redenen wisselen we ze om. Voor de derde keer vergelijken we 8 en 2 en in ieder geval 8 en 5. We hebben in totaal vier uitwisselingen gedaan: (8, 7), (8, 1), (8, 2) en (8, 5). Een waarde van 8, de grootste in deze array, verscheen aan het einde van de lijst op de juiste positie. 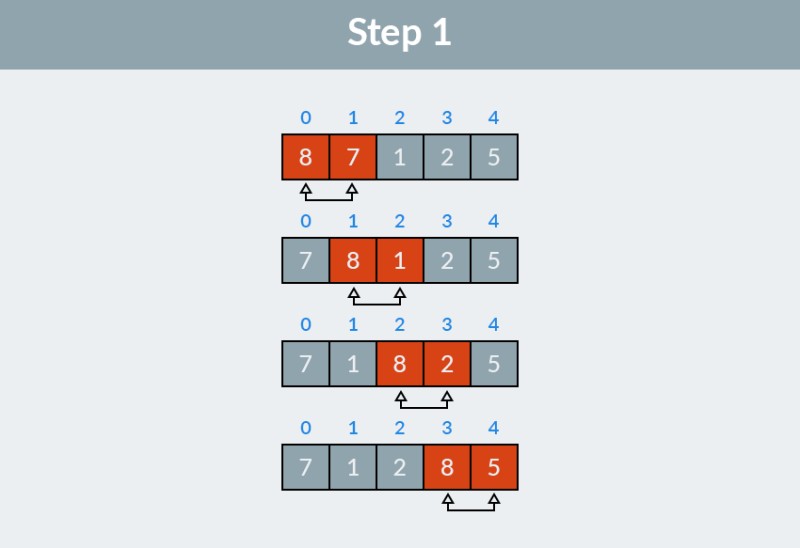 Het resultaat van de eerste stap van het Bubble sort-algoritme is de volgende array:
Het resultaat van de eerste stap van het Bubble sort-algoritme is de volgende array:  Stap 2. Doe hetzelfde met (7,1), (7,2) en (7,5). 7 staat nu op de voorlaatste plaats en we hoeven het niet te vergelijken met de "staart" van de lijst, het is al gesorteerd.
Stap 2. Doe hetzelfde met (7,1), (7,2) en (7,5). 7 staat nu op de voorlaatste plaats en we hoeven het niet te vergelijken met de "staart" van de lijst, het is al gesorteerd.  Het resultaat van de tweede stap van het Bubble sort-algoritme is de volgende array:
Het resultaat van de tweede stap van het Bubble sort-algoritme is de volgende array:  Zoals u kunt zien, is deze array al gesorteerd. Hoe dan ook, het Bubble Sort-algoritme zou nog minstens één keer aan de slag moeten gaan. Stap 3. We gaan nog een keer door de array. Niets om hier te ruilen, dus als we het "verbeterde" Bubble Sort-algoritme gebruiken (met controle of er ten minste één uitwisseling bij de vorige stap is gemaakt), is deze stap de laatste.
Zoals u kunt zien, is deze array al gesorteerd. Hoe dan ook, het Bubble Sort-algoritme zou nog minstens één keer aan de slag moeten gaan. Stap 3. We gaan nog een keer door de array. Niets om hier te ruilen, dus als we het "verbeterde" Bubble Sort-algoritme gebruiken (met controle of er ten minste één uitwisseling bij de vorige stap is gemaakt), is deze stap de laatste.
Bubble sort Java-code
Bellen sorteren Java-realisatie
Laten we twee methoden maken voor bellensortering. De eerste, bubbleSort(int[] myArray) is een vlakke. Het loopt elke keer door de array. De tweede, OptimizedBubbleSort(int myArray[]), wordt geoptimaliseerd door het algoritme te stoppen als de binnenste lus geen swap heeft veroorzaakt. Teller laat zien hoeveel stappen je hebt gedaan tijdens het sorteren. Hier hebben we Bubble sort Java-realisatie:
import java.util.Arrays;
public class BubbleSortExample {
// Plane Bubble sort example
public static int[] bubbleSort(int[] myArray) {
int temp = 0; // temporary element for swapping
int counter = 0; // element to count quantity of steps
for (int i = 0; i < myArray.length; i++) {
counter = i + 1;
for (int j = 1; j < (myArray.length - i); j++) {
if (myArray[j - 1] > myArray[j]) {
// swap array’s elements using temporary element
temp = myArray[j - 1];
myArray[j - 1] = myArray[j];
myArray[j] = temp;
}
}
}
System.out.println("Steps quantity, non optimized = " + counter);
return myArray;
}
// An optimized version of Java Bubble Sorting
static int[] optimizedBubbleSort(int myArray[]) {
int temp;
boolean swapped;
int counter = 0; // element to count quantity of steps
for (int i = 0; i < myArray.length - 1; i++) {
counter = i + 1;
swapped = false;
for (int j = 0; j < myArray.length - i - 1; j++) {
// counter++;
if (myArray[j] > myArray[j + 1]) {
// swap arr[j] and arr[j+1]
temp = myArray[j];
myArray[j] = myArray[j + 1];
myArray[j + 1] = temp;
swapped = true;
}
} // counter = i;
// If there weren't elements to swap in inner loop, then break
if (swapped == false) {
break;
}
}
System.out.println("steps quantity, optimized = " + counter);
return myArray;
}
public static void main(String[] args) {
int arr[] = {8, 7, 1, 2, 5};
int arr1[] = {8, 7, 1, 2, 5};
System.out.println("Array arr Before Bubble Sort");
// we use java.util.Arrays toString method to print the array
System.out.println(Arrays.toString(arr));
System.out.println("Array arr After Bubble Sort");
System.out.println(Arrays.toString(bubbleSort(arr)));
System.out.println("Array arr1 Before Bubble Sort");
System.out.println(Arrays.toString(arr1));
System.out.println("Array arr1 After Optimized Bubble Sort");
System.out.println(Arrays.toString(optimizedBubbleSort(arr1)));
}
}
Array arr Before Bubble Sort
[8, 7, 1, 2, 5]
Array arr After Bubble Sort
Steps quantity, non optimized = 5
[1, 2, 5, 7, 8]
Array arr1 Before Bubble Sort
[8, 7, 1, 2, 5]
Array arr1 After Optimized Bubble Sort
steps quantity, optimized = 3
[1, 2, 5, 7, 8]


GO TO FULL VERSION