If you have ever heard of sorting methods in programming, most likely it was the bubble sort algorithm. It is a famous one. Every programmer knows bubble sort (or at least heard of it while learning) not because it is the best sorting algorithm in the world, but the easiest one. This algorithm is usually used for learning purposes or you may get it as a task in your Java Junior Interview. Java Bubble sort algorithm is very easy to understand, however it is not an efficient one. Anyway, let’s figure it out.
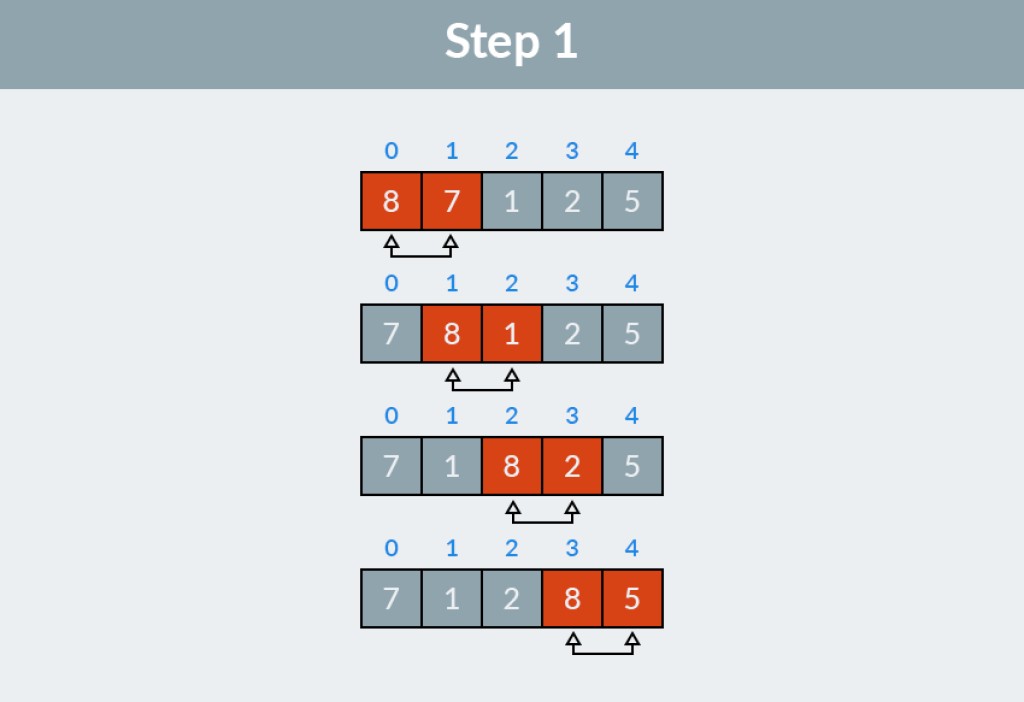
![Bubble sort - 2]() Step 1: we are going through the array. The algorithm starts with the first two elements (with indices 0 and 1), 8 and 7, and checks if they are in the correct order. Obviously, 8 > 7, so we swap them. Next, we look at the second and third elements (indices 1 and 2), now these are 8 and 1. For the same reasons, we swap them. For the third time we compare 8 and 2 and, at least 8 and 5. We made four exchanges in total: (8, 7), (8, 1), (8, 2) and (8, 5). A value of 8, the biggest in this array, popped up at the end of the list to the correct position.
Step 1: we are going through the array. The algorithm starts with the first two elements (with indices 0 and 1), 8 and 7, and checks if they are in the correct order. Obviously, 8 > 7, so we swap them. Next, we look at the second and third elements (indices 1 and 2), now these are 8 and 1. For the same reasons, we swap them. For the third time we compare 8 and 2 and, at least 8 and 5. We made four exchanges in total: (8, 7), (8, 1), (8, 2) and (8, 5). A value of 8, the biggest in this array, popped up at the end of the list to the correct position.
![Bubble sort - 3]() The result of the first step of Bubble sort algorithm working is the next array:
The result of the first step of Bubble sort algorithm working is the next array:
![Bubble sort - 4]() Step 2. Doing the same with (7,1), (7,2) and (7,5). 7 is now in the penultimate position, and we don’t need to compare it with the "tail" of the list, it is already sorted.
Step 2. Doing the same with (7,1), (7,2) and (7,5). 7 is now in the penultimate position, and we don’t need to compare it with the "tail" of the list, it is already sorted.
![Bubble sort - 5]() The result of the second step of Bubble sort algorithm working is the next array:
The result of the second step of Bubble sort algorithm working is the next array:
![Bubble sort - 6]() As you may see, this array is already sorted. Anyway Bubble Sort algorithm should get going at least one more time.
Step3. We are going through the array once more. Nothing to swap here, so if we are using “improved” Bubble Sort algorithm (with checking out if at least one exchange at the previous step was made) this step is the last one.
As you may see, this array is already sorted. Anyway Bubble Sort algorithm should get going at least one more time.
Step3. We are going through the array once more. Nothing to swap here, so if we are using “improved” Bubble Sort algorithm (with checking out if at least one exchange at the previous step was made) this step is the last one.
What is sorting
First of all, you need to understand what sorting is in general and what we can sort in Java programs. If we can compare two or more elements or objects by any of their attributes, it means that they can be sorted by this attribute. For example, numbers in ascending or descending order or words alphabetically. Hence, the elements must be comparable with each other. By the way, the elements of what? In Java, we can compare the elements of Collections. For example we can sort Array or ArrayList of integers, Strings and so on.How does bubble sort work
Let's say, we need to sort an array of integers in ascending order, that is, from the smallest to the biggest number. First, we are going along the entire array and compare every 2 neighboring elements. If they are in the wrong order (the left neighbor is bigger than the right one), we swap them. At the first pass at the end it will appear the biggest element (if we sort in ascending order). You may say, the biggest element “pops up”. That’s the reason of the Bubble sort algorithm name. We repeat the first step from the first to the next-to-last element. We’ve got the second biggest element at the next-to-last place. And so on. We can improve an algorithm a little bit with checking out if at least one exchange at the previous step was made. If it isn’t we stop our running along the array.Bubble sort example
Let's sort the array of integers, the one, you may see below on a picture. Step 1: we are going through the array. The algorithm starts with the first two elements (with indices 0 and 1), 8 and 7, and checks if they are in the correct order. Obviously, 8 > 7, so we swap them. Next, we look at the second and third elements (indices 1 and 2), now these are 8 and 1. For the same reasons, we swap them. For the third time we compare 8 and 2 and, at least 8 and 5. We made four exchanges in total: (8, 7), (8, 1), (8, 2) and (8, 5). A value of 8, the biggest in this array, popped up at the end of the list to the correct position.
Step 1: we are going through the array. The algorithm starts with the first two elements (with indices 0 and 1), 8 and 7, and checks if they are in the correct order. Obviously, 8 > 7, so we swap them. Next, we look at the second and third elements (indices 1 and 2), now these are 8 and 1. For the same reasons, we swap them. For the third time we compare 8 and 2 and, at least 8 and 5. We made four exchanges in total: (8, 7), (8, 1), (8, 2) and (8, 5). A value of 8, the biggest in this array, popped up at the end of the list to the correct position.
 The result of the first step of Bubble sort algorithm working is the next array:
The result of the first step of Bubble sort algorithm working is the next array:
 Step 2. Doing the same with (7,1), (7,2) and (7,5). 7 is now in the penultimate position, and we don’t need to compare it with the "tail" of the list, it is already sorted.
Step 2. Doing the same with (7,1), (7,2) and (7,5). 7 is now in the penultimate position, and we don’t need to compare it with the "tail" of the list, it is already sorted.
 The result of the second step of Bubble sort algorithm working is the next array:
The result of the second step of Bubble sort algorithm working is the next array:
 As you may see, this array is already sorted. Anyway Bubble Sort algorithm should get going at least one more time.
Step3. We are going through the array once more. Nothing to swap here, so if we are using “improved” Bubble Sort algorithm (with checking out if at least one exchange at the previous step was made) this step is the last one.
As you may see, this array is already sorted. Anyway Bubble Sort algorithm should get going at least one more time.
Step3. We are going through the array once more. Nothing to swap here, so if we are using “improved” Bubble Sort algorithm (with checking out if at least one exchange at the previous step was made) this step is the last one.
Bubble sort Java code
Bubble sort Java realisation
Let’s create two methods for Bubble sort. The first one, bubbleSort(int[] myArray) is a plane one. It runs through the array every time. The second one, optimizedBubbleSort(int myArray[]) is optimized by stopping the algorithm if inner loop didn’t cause any swap. Counter shows you how many steps did you do while sorting. Here we’ve got Bubble sort Java realisation:
import java.util.Arrays;
public class BubbleSortExample {
// Plane Bubble sort example
public static int[] bubbleSort(int[] myArray) {
int temp = 0; // temporary element for swapping
int counter = 0; // element to count quantity of steps
for (int i = 0; i < myArray.length; i++) {
counter = i + 1;
for (int j = 1; j < (myArray.length - i); j++) {
if (myArray[j - 1] > myArray[j]) {
// swap array’s elements using temporary element
temp = myArray[j - 1];
myArray[j - 1] = myArray[j];
myArray[j] = temp;
}
}
}
System.out.println("Steps quantity, non optimized = " + counter);
return myArray;
}
// An optimized version of Java Bubble Sorting
static int[] optimizedBubbleSort(int myArray[]) {
int temp;
boolean swapped;
int counter = 0; // element to count quantity of steps
for (int i = 0; i < myArray.length - 1; i++) {
counter = i + 1;
swapped = false;
for (int j = 0; j < myArray.length - i - 1; j++) {
// counter++;
if (myArray[j] > myArray[j + 1]) {
// swap arr[j] and arr[j+1]
temp = myArray[j];
myArray[j] = myArray[j + 1];
myArray[j + 1] = temp;
swapped = true;
}
} // counter = i;
// If there weren't elements to swap in inner loop, then break
if (swapped == false) {
break;
}
}
System.out.println("steps quantity, optimized = " + counter);
return myArray;
}
public static void main(String[] args) {
int arr[] = {8, 7, 1, 2, 5};
int arr1[] = {8, 7, 1, 2, 5};
System.out.println("Array arr Before Bubble Sort");
// we use java.util.Arrays toString method to print the array
System.out.println(Arrays.toString(arr));
System.out.println("Array arr After Bubble Sort");
System.out.println(Arrays.toString(bubbleSort(arr)));
System.out.println("Array arr1 Before Bubble Sort");
System.out.println(Arrays.toString(arr1));
System.out.println("Array arr1 After Optimized Bubble Sort");
System.out.println(Arrays.toString(optimizedBubbleSort(arr1)));
}
}
Array arr Before Bubble Sort
[8, 7, 1, 2, 5]
Array arr After Bubble Sort
Steps quantity, non optimized = 5
[1, 2, 5, 7, 8]
Array arr1 Before Bubble Sort
[8, 7, 1, 2, 5]
Array arr1 After Optimized Bubble Sort
steps quantity, optimized = 3
[1, 2, 5, 7, 8]


GO TO FULL VERSION