बबल सॉर्ट जावा

जर तुम्ही प्रोग्रामिंगमधील क्रमवारी पद्धतींबद्दल ऐकले असेल, तर बहुधा ते बबल सॉर्ट अल्गोरिदम होते. तो एक प्रसिद्ध आहे. प्रत्येक प्रोग्रामरला बबल सॉर्ट माहित असते (किंवा शिकत असताना किमान ते ऐकले असते) कारण ते जगातील सर्वोत्तम क्रमवारी अल्गोरिदम आहे, परंतु सर्वात सोपा आहे. हा अल्गोरिदम सहसा शिकण्याच्या उद्देशाने वापरला जातो किंवा तुम्हाला तुमच्या जावा ज्युनियर मुलाखतीत एक कार्य म्हणून मिळू शकेल. जावा बबल सॉर्ट अल्गोरिदम समजणे खूप सोपे आहे, तथापि ते कार्यक्षम नाही. असो, चला ते काढूया.

काय वर्गीकरण आहे

सर्व प्रथम, आपल्याला हे समजून घेणे आवश्यक आहे की सर्वसाधारणपणे सॉर्टिंग काय आहे आणि आम्ही Java प्रोग्राम्समध्ये काय क्रमवारी लावू शकतो. जर आपण दोन किंवा अधिक घटकांची किंवा वस्तूंची त्यांच्या कोणत्याही गुणधर्मांद्वारे तुलना करू शकलो, तर याचा अर्थ असा होतो की या गुणधर्मांद्वारे त्यांची क्रमवारी लावली जाऊ शकते. उदाहरणार्थ, चढत्या किंवा उतरत्या क्रमाने संख्या किंवा वर्णक्रमानुसार शब्द. म्हणून, घटक एकमेकांशी तुलना करणे आवश्यक आहे. तसे, कशाचे घटक? Java मध्ये, आपण कलेक्शनच्या घटकांची तुलना करू शकतो. उदाहरणार्थ आपण पूर्णांक, स्ट्रिंग्स इत्यादींची Array किंवा ArrayList क्रमवारी लावू शकतो.

बबल सॉर्ट कसे कार्य करते

समजा, आपल्याला पूर्णांकांची अॅरे चढत्या क्रमाने क्रमवारी लावायची आहे, म्हणजेच सर्वात लहान ते मोठ्या संख्येपर्यंत. प्रथम, आपण संपूर्ण अॅरेच्या बाजूने जात आहोत आणि प्रत्येक 2 शेजारच्या घटकांची तुलना करतो. जर ते चुकीच्या क्रमाने असतील (डावा शेजारी उजव्या शेजारीपेक्षा मोठा असेल), आम्ही त्यांना स्वॅप करतो. शेवटी पहिल्या पासवर तो सर्वात मोठा घटक दिसेल (जर आपण चढत्या क्रमाने क्रमवारी लावली तर). तुम्ही म्हणू शकता, सर्वात मोठा घटक “पॉप अप” आहे. हे बबल सॉर्ट अल्गोरिदम नावाचे कारण आहे. आम्ही पहिल्या चरणापासून पुढील ते शेवटच्या घटकापर्यंतची पहिली पायरी पुन्हा करतो. आम्हाला पुढच्या-ते-शेवटच्या ठिकाणी दुसरा सर्वात मोठा घटक मिळाला आहे. वगैरे. आधीच्या पायरीवर किमान एक एक्सचेंज केले होते का ते तपासून आम्ही अल्गोरिदम थोडे सुधारू शकतो. जर तसे नसेल तर आम्ही अ‍ॅरेसह आमचे धावणे थांबवतो.

बबल क्रमवारी उदाहरण

पूर्णांकांच्या अ‍ॅरेची क्रमवारी लावू, एक, तुम्ही खाली चित्रात पाहू शकता. पायरी 1: आपण अॅरेमधून जात आहोत. अल्गोरिदम पहिल्या दोन घटकांपासून सुरू होते (निर्देशांक 0 आणि 1 सह), 8 आणि 7, आणि ते योग्य क्रमाने आहेत का ते तपासते. अर्थात, 8 > 7, म्हणून आम्ही ते स्वॅप करतो. पुढे, आम्ही दुसरे आणि तिसरे घटक (निर्देशांक 1 आणि 2) पाहतो, आता हे 8 आणि 1 आहेत. त्याच कारणांसाठी, आम्ही त्यांची अदलाबदल करतो. तिसऱ्यांदा आम्ही 8 आणि 2 आणि किमान 8 आणि 5 ची तुलना करतो. आम्ही एकूण चार एक्सचेंज केले: (8, 7), (8, 1), (8, 2) आणि (8, 5). 8 चे मूल्य, या अॅरेमधील सर्वात मोठे, सूचीच्या शेवटी योग्य स्थानावर पॉप अप होते. 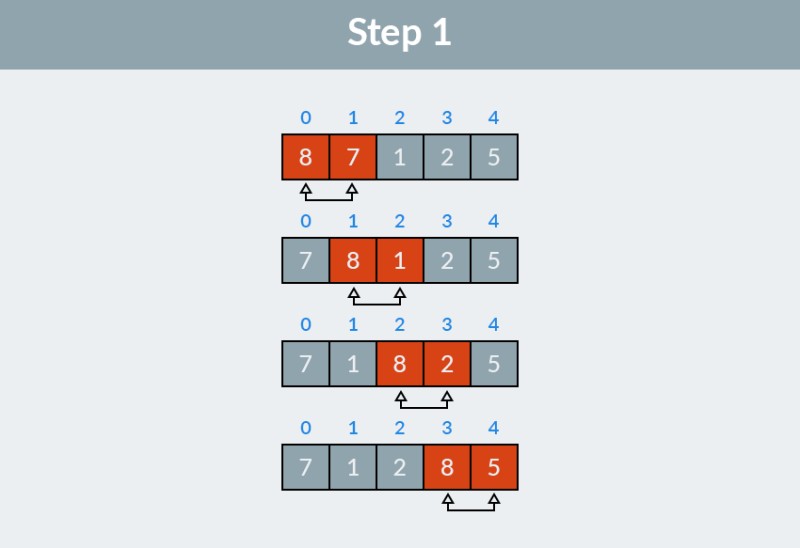बबल सॉर्ट अल्गोरिदमच्या पहिल्या चरणाचा परिणाम पुढील अॅरे आहे: पायरी 2. (7,1), (7,2) आणि (7,5) सह असेच करणे. 7 आता अंतिम स्थितीत आहे आणि आम्हाला त्याची सूचीच्या "शेपटी" शी तुलना करण्याची आवश्यकता नाही, ती आधीच क्रमवारी लावलेली आहे. बबल सॉर्ट अल्गोरिदमच्या दुसऱ्या पायरीचा परिणाम पुढील अॅरे आहे: जसे तुम्ही पाहू शकता, ही अॅरे आधीच क्रमवारी लावलेली आहे. असं असलं तरी बबल सॉर्ट अल्गोरिदम कमीत कमी आणखी एक वेळ चालू ठेवला पाहिजे. पायरी 3. आम्ही पुन्हा एकदा अॅरेमधून जात आहोत. येथे अदलाबदल करण्यासाठी काहीही नाही, म्हणून जर आपण "सुधारित" बबल सॉर्ट अल्गोरिदम वापरत असाल तर (मागील पायरीवर किमान एक एक्सचेंज केले गेले आहे का ते तपासून) ही पायरी शेवटची आहे.

बबल सॉर्ट जावा कोड

बबल क्रमवारी जावा साकार

बबल क्रमवारीसाठी दोन पद्धती बनवू. पहिला, bubbleSort(int[] myArray) एक विमान आहे. हे प्रत्येक वेळी अॅरेमधून चालते. दुसरा, ऑप्टिमाइझ्ड बबलसॉर्ट(int myArray[]) अल्गोरिदम थांबवून ऑप्टिमाइझ केला जातो जर आतील लूपमुळे कोणतेही स्वॅप होत नसेल. काउंटर तुम्हाला क्रमवारी लावताना तुम्ही किती पायऱ्या केल्या हे दाखवते. येथे आम्हाला बबल सॉर्ट जावा रिअलायझेशन मिळाले आहे:

import java.util.Arrays;

public class BubbleSortExample {

   //  Plane Bubble sort example

   public static int[] bubbleSort(int[] myArray) {

       int temp = 0;  //  temporary element for swapping
       int counter = 0;  //  element to count quantity of steps

       for (int i = 0; i < myArray.length; i++) {
           counter = i + 1;
           for (int j = 1; j < (myArray.length - i); j++) {

               if (myArray[j - 1] > myArray[j]) {
                   //  swap array’s elements using temporary element
                   temp = myArray[j - 1];
                   myArray[j - 1] = myArray[j];
                   myArray[j] = temp;
               }
           }
       }
       System.out.println("Steps quantity, non optimized = " + counter);
       return myArray;
   }
   //  An optimized version of Java Bubble Sorting

   static int[] optimizedBubbleSort(int myArray[]) {
       int temp;
       boolean swapped;
       int counter = 0;  //  element to count quantity of steps
       for (int i = 0; i < myArray.length - 1; i++) {
           counter = i + 1;
           swapped = false;
           for (int j = 0; j < myArray.length - i - 1; j++) {
               //  counter++;
               if (myArray[j] > myArray[j + 1]) {
                   //  swap arr[j] and arr[j+1]
                   temp = myArray[j];
                   myArray[j] = myArray[j + 1];
                   myArray[j + 1] = temp;
                   swapped = true;

               }
           }  //  counter = i;
           //  If there weren't elements to swap in inner loop, then break
           if (swapped == false) {

               break;

           }
       }
       System.out.println("steps quantity, optimized = " + counter);
       return myArray;
   }


   public static void main(String[] args) {
       int arr[] = {8, 7, 1, 2, 5};
       int arr1[] = {8, 7, 1, 2, 5};

       System.out.println("Array arr Before Bubble Sort");
       //  we use java.util.Arrays toString method to print the array  
 System.out.println(Arrays.toString(arr));

       System.out.println("Array arr After Bubble Sort");
       System.out.println(Arrays.toString(bubbleSort(arr)));

       System.out.println("Array arr1 Before Bubble Sort");
       System.out.println(Arrays.toString(arr1));

       System.out.println("Array arr1 After Optimized Bubble Sort");
       System.out.println(Arrays.toString(optimizedBubbleSort(arr1)));
   }
}

बबल सॉर्ट जावा अल्गोरिदम कार्याचा परिणाम:

Array arr Before Bubble Sort
[8, 7, 1, 2, 5]
Array arr After Bubble Sort
Steps quantity, non optimized = 5
[1, 2, 5, 7, 8]
Array arr1 Before Bubble Sort
[8, 7, 1, 2, 5]
Array arr1 After Optimized Bubble Sort
steps quantity, optimized = 3
[1, 2, 5, 7, 8]

बबल क्रमवारी किती कार्यक्षम आहे?

बबल सॉर्ट हे अंमलात आणण्यासाठी सर्वात सोपा अल्गोरिदम आहे परंतु ते कार्यक्षम नाही. यासाठी नेस्टेड लूपची जोडी आवश्यक आहे. अगदी सर्वात वाईट परिस्थितीत अल्गोरिदमच्या ऑप्टिमाइझ केलेल्या आवृत्तीमध्ये (डेटा सेटचा प्रत्येक घटक इच्छित घटकाच्या उलट क्रमाने असतो) डेटा सेटच्या प्रत्येक n घटकांसाठी बाह्य लूप एकदाच पुनरावृत्ती होते . आतील लूप पहिल्यांदा n वेळा पुनरावृत्ती होते, ( n-1 ) दुसऱ्यासाठी, आणि असेच. म्हणून, सर्व n , घटकांची क्रमवारी लावण्यासाठी , लूप n*(n-1)/2 वेळा कार्यान्वित करणे आवश्यक आहे. त्याला O(n ² ) म्हणतातवेळेची जटिलता आणि याचा अर्थ असा की अल्गोरिदम अॅरेच्या 1000 घटकांसाठी सुमारे 500 000 तुलना करते. तथापि, बबल सॉर्ट अल्गोरिदम मेमरी वापरामध्ये खूपच प्रभावी आहे (मेमरी जटिलता O(n) आहे ) आणि जवळजवळ क्रमवारी लावलेल्या लहान डेटासेटसाठी खरोखर चांगले आहे.