"Hi, Amigo!"
"Hello, Rishi!"
"I found my old notes over there and prepared some interesting material for you. I think you'll be interested in hearing it."
"Let's hear it. You always find something interesting that later proves to be very useful."
"OK. Today I want to tell you about trees, so I will begin with graphs."
"A graph is a system of points and lines that connect them. The points are called the vertices of the graph, and the lines are called the edges of the graph. For example:"

"A graph is very convenient to use as a mathematical model for various real-world processes and tasks. Many different tasks and algorithms have been invented for graphs, so they are used fairly often."
"For example, suppose vertices are cities, and edges are roads. Then searching for the shortest road between cities becomes: «given a graph, find the shortest path between two vertices»."
"But the path from A to B isn't always the same as the path from B to A. So, sometimes having two different lines is preferred. To do this, the lines (edges of the graph) are replaced with arrows. In other words, the graph can have two arrows: one from A to B, and another from B to A."
"If the graph uses arrows, then it is called a directed graph; if it just has lines, then it is called an undirected graph."
"Each vertex can have its own number of edges. A vertex can also have no edges at all. Conversely, a vertex can be connected by edges to every other vertex. If each pair of vertices in a graph is connected by an edge, then it is called a complete graph."
"If you can use edges to reach every vertex in a graph, then it is called a connected graph. A graph that has three separate vertices and no edges is still a graph, but we call it a disconnected graph."
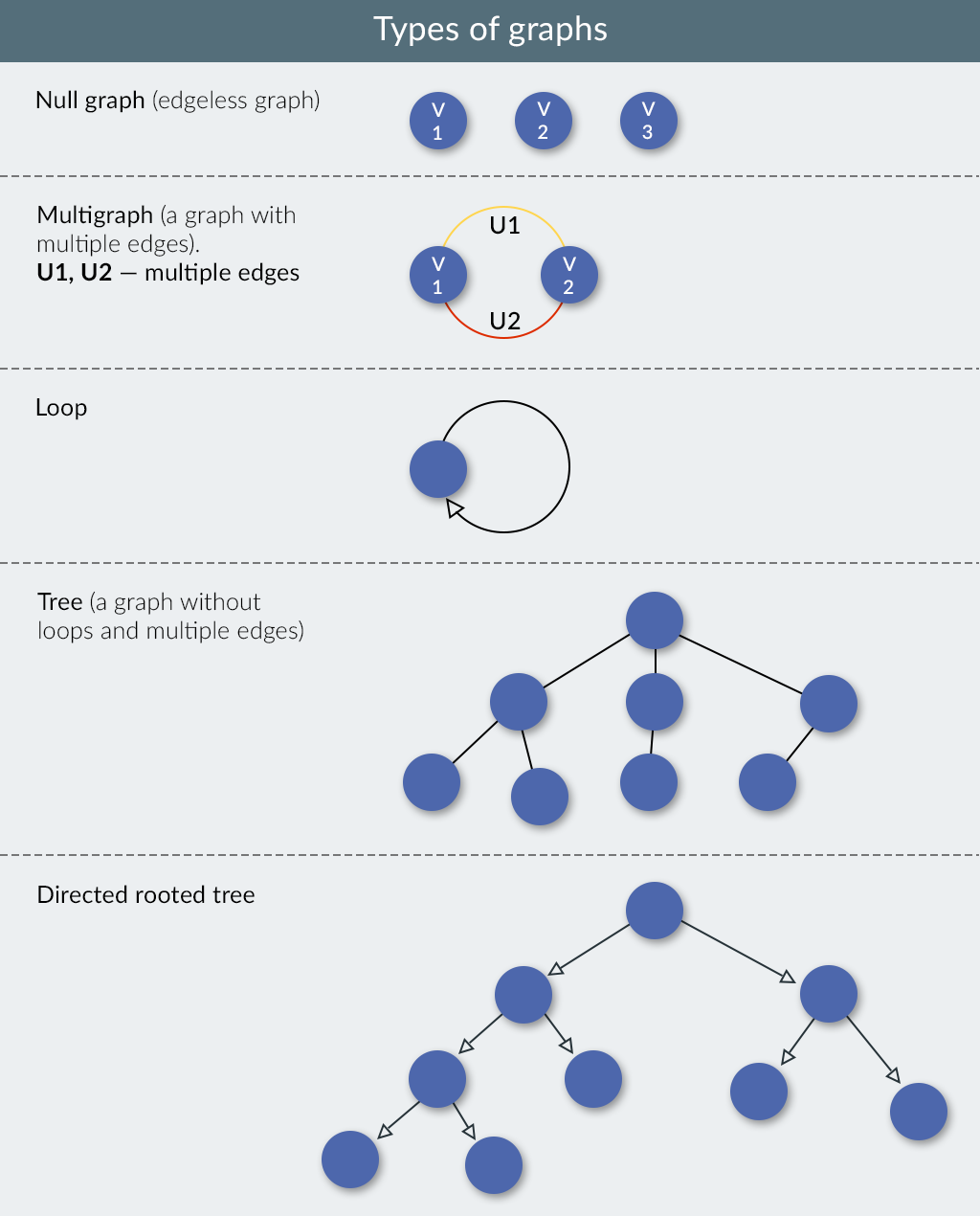
"To form a connected graph from N vertices, you need at least N-1 edges. This type of graph is called a tree."
"Moreover, usually one vertex is chosen to be the tree's root, and the rest are declared to be branches. Tree branches that do not have their own branches are called leaves. For example:"

"If each element of the tree has two children, then it is called a binary tree. In other words, there can be either 0 or 2 branches. You can see a binary tree in the upper right."
"A tree is called a complete binary tree when each branch has 2 children, and all the leaves (vertices without children) are on the same row."
"For example:"

"Why are these trees needed?"
"Oh, trees are used in lots of places. In general, binary trees are sorted structured data."
"What's that?"
"Yes, it's very simple. We store a certain value in each vertex. And each element follows a rule: the value stored in the right child must be greater than the value stored in the vertex, and the value stored in the left child must be less than the value stored in the vertex. This ordering makes it possible to quickly find the elements of the tree that you need."
"Can you clarify what that means?"
"Tree elements are usually sorted by adding. Suppose we have 7 elements: 13, 5, 4, 16, 8, 11, 10"
"Here is how the elements are added to the tree."

"If we are looking for the number 7 in this tree, then this is how the search will go"
"0) Start at the root."
"1a) Is 7 equal to 13? No"
"1b) Is 7 greater than 13? No, so we move to the left subtree."
"2a) Is 7 equal to 5? No."
"2b) Is 7 greater than 5? Yes, so we move to the right subtree."
"3a) Is 7 equal to 8? No"
"3b) Is 7 greater than 8? No, so we move to the left subtree."
"4a) There is no left subtree, which means the number 7 is not in the tree."
"Ah. In other words, we only need to check the vertices on the path from the root to the would-be location of the desired number. Yeah, that really is fast."
"What's more, if the tree is balanced, then you will only need to pass through about 20 vertices to search a million elements."
"I agree — that's not very many."
"What do you mean by balanced tree?"
"A tree that isn't distorted, i.e. that doesn't have long branches. For example, if the elements were already sorted when we built the tree, then we would have made a very long tree consisting of one branch."
"Hmm. You're right. So what do we do?"
"As you have probably already guessed, the most efficient tree has branches that are approximately the same length. Then each comparison discards the largest part of the remaining subtree."
"So, we need to rebuild the tree?"
"Yep. It needs to be «balanced» — to be made as close as possible to a complete binary tree."
"To solve this problem, self-balancing trees were invented. If the tree becomes distorted after adding an element, then it reorders the elements slightly to make everything OK. Here's an example of balancing:"

"Some of these trees are known as red-black trees."
"Why are they called red-black?"
"Their inventor drew all the vertices using two colors. One color was red, and the other was black. The different vertices obey different rules. This forms the entire basis for the balancing procedure."
"For example:"
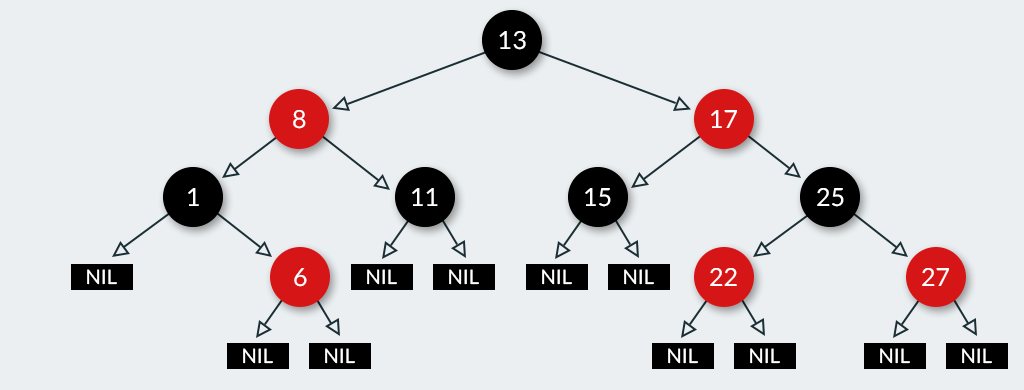
"So what are these rules?"
"1) A red vertex cannot be the child of a red vertex."
"2) The black depth of every leaf is the same (black depth refers to the number of black vertices on the path from the root)."
"3) The root of the tree is black."
"I won't explain how this works — you're head is probably already exploding."
"Yes. My processor is giving off a little smoke."
"Here's a link for you. If you want, you can read more about it here."
"And now, go take a break."

GO TO FULL VERSION