एल्गोरिथम जटिलता

नमस्ते! आज का पाठ बाकियों से थोड़ा अलग होगा। यह अलग होगा कि यह केवल अप्रत्यक्ष रूप से जावा से संबंधित है। उस ने कहा, यह विषय हर प्रोग्रामर के लिए बहुत महत्वपूर्ण है। हम एल्गोरिदम के बारे में बात करने जा रहे हैं । एक एल्गोरिदम क्या है? सरल शब्दों में, यह क्रियाओं का कुछ क्रम है जिसे वांछित परिणाम प्राप्त करने के लिए पूरा किया जाना चाहिए । हम रोजमर्रा की जिंदगी में अक्सर एल्गोरिदम का इस्तेमाल करते हैं। उदाहरण के लिए, हर सुबह आपके पास एक विशिष्ट कार्य होता है: स्कूल या काम पर जाना, और उसी समय:

• पहने
• साफ़
• सिंचित

कौन सा एल्गोरिदम आपको यह परिणाम प्राप्त करने देता है?

1. अलार्म घड़ी का उपयोग करके जागें।
2. स्नान करो और अपने आप को धो लो।
3. नाश्ता और कुछ कॉफी या चाय बनाओ।
4. खाना।
5. यदि आपने पिछली शाम को अपने कपड़ों को प्रेस नहीं किया है, तो उन्हें आयरन करें।
6. कपड़े पहनो।
7. घर छोड़ें।

कार्यों का यह क्रम निश्चित रूप से आपको वांछित परिणाम प्राप्त करने में मदद करेगा। प्रोग्रामिंग में, हम कार्यों को पूरा करने के लिए लगातार काम कर रहे हैं। इन कार्यों का एक महत्वपूर्ण हिस्सा पहले से ही ज्ञात एल्गोरिदम का उपयोग करके किया जा सकता है। उदाहरण के लिए, मान लें कि आपका कार्य यह है: किसी सरणी में 100 नामों की सूची क्रमबद्ध करें । यह कार्य काफी सरल है, लेकिन इसे विभिन्न तरीकों से हल किया जा सकता है। यहाँ एक संभावित समाधान है: नामों को वर्णानुक्रम में छाँटने के लिए एल्गोरिथम:

1. वेबस्टर्स थर्ड न्यू इंटरनेशनल डिक्शनरी का 1961 संस्करण खरीदें या डाउनलोड करें।
2. इस शब्दकोश में हमारी सूची से हर नाम खोजें।
3. कागज के एक टुकड़े पर, शब्दकोश का वह पृष्ठ लिखें जिस पर नाम स्थित है।
4. नामों को क्रमबद्ध करने के लिए कागज के टुकड़ों का प्रयोग करें।

क्या क्रियाओं का ऐसा क्रम हमारे कार्य को पूरा करेगा? हां, जरूर होगा। क्या यह उपाय कारगर है ? मुश्किल से। यहां हम एल्गोरिथम के एक और बहुत महत्वपूर्ण पहलू पर आते हैं: उनकी दक्षता । इस कार्य को पूरा करने के कई तरीके हैं। लेकिन प्रोग्रामिंग और सामान्य जीवन दोनों में, हम सबसे कुशल तरीका चुनना चाहते हैं। यदि आपका काम मक्खन लगा टोस्ट बनाना है, तो आप गेहूँ बोकर और गाय दुह कर शुरुआत कर सकते हैं। लेकिन वह एक अक्षम होगासमाधान — इसमें काफ़ी समय लगेगा और बहुत पैसा खर्च होगा। आप केवल रोटी और मक्खन खरीदकर अपना सरल कार्य पूरा कर सकते हैं। हालांकि यह आपको समस्या को हल करने देता है, गेहूं और एक गाय को शामिल करने वाला एल्गोरिदम अभ्यास में उपयोग करने के लिए बहुत जटिल है। प्रोग्रामिंग में, हमारे पास एल्गोरिदम की जटिलता का आकलन करने के लिए बिग ओ नोटेशन नामक विशेष संकेतन है। बिग ओ यह आकलन करना संभव बनाता है कि एल्गोरिदम का निष्पादन समय इनपुट डेटा आकार पर कितना निर्भर करता है । आइए सबसे सरल उदाहरण देखें: डेटा ट्रांसफर। कल्पना कीजिए कि आपको लंबी दूरी (उदाहरण के लिए, 5000 मील) पर फ़ाइल के रूप में कुछ जानकारी भेजने की आवश्यकता है। कौन सा एल्गोरिदम सबसे कुशल होगा? यह उस डेटा पर निर्भर करता है जिसके साथ आप काम कर रहे हैं। उदाहरण के लिए, मान लीजिए कि हमारे पास एक ऑडियो फ़ाइल है जो 10 एमबी की है। इस मामले में, इंटरनेट पर फ़ाइल भेजने के लिए सबसे कुशल एल्गोरिथ्म है। इसमें एक-दो मिनट से ज्यादा नहीं लग सकता था! आइए हमारे एल्गोरिदम को दोबारा दोहराएं: "यदि आप 5000 मील की दूरी पर फ़ाइलों के रूप में जानकारी स्थानांतरित करना चाहते हैं, तो आपको इंटरनेट के माध्यम से डेटा भेजना चाहिए"। उत्कृष्ट। अब इसका विश्लेषण करते हैं। क्या यह हमारे कार्य को पूरा करता है?अच्छा, हाँ, यह करता है। लेकिन हम इसकी जटिलता के बारे में क्या कह सकते हैं? हम्म, अब चीजें और दिलचस्प होती जा रही हैं। तथ्य यह है कि हमारा एल्गोरिदम इनपुट डेटा, अर्थात् फाइलों के आकार पर बहुत निर्भर है। अगर हमारे पास 10 मेगाबाइट हैं, तो सब कुछ ठीक है। लेकिन क्या होगा अगर हमें 500 मेगाबाइट भेजने की जरूरत है? 20 गीगाबाइट? 500 टेराबाइट्स? 30 पेटाबाइट्स? क्या हमारा एल्गोरिदम काम करना बंद कर देगा? नहीं, डेटा की इन सभी मात्राओं को वास्तव में स्थानांतरित किया जा सकता है। क्या इसमें अधिक समय लगेगा? हाँ मैं करूंगा! अब हम अपने एल्गोरिथम की एक महत्वपूर्ण विशेषता जानते हैं: भेजने के लिए जितना अधिक डेटा होगा, एल्गोरिथम को चलाने में उतना ही अधिक समय लगेगा. लेकिन हम इस रिश्ते की अधिक सटीक समझ चाहते हैं (इनपुट डेटा आकार और इसे भेजने के लिए आवश्यक समय के बीच)। हमारे मामले में, एल्गोरिथम जटिलता रैखिक है । "रैखिक" का अर्थ है कि जैसे-जैसे इनपुट डेटा की मात्रा बढ़ती है, इसे भेजने में लगने वाला समय लगभग आनुपातिक रूप से बढ़ जाएगा। यदि डेटा की मात्रा दोगुनी हो जाती है, तो इसे भेजने में लगने वाला समय दोगुना हो जाएगा। अगर डेटा 10 गुना बढ़ जाता है, तो ट्रांसमिशन का समय 10 गुना बढ़ जाएगा। बिग ओ नोटेशन का उपयोग करते हुए, हमारे एल्गोरिदम की जटिलता को ओ (एन) के रूप में व्यक्त किया जाता है. आपको भविष्य के लिए इस संकेतन को याद रखना चाहिए - यह हमेशा रैखिक जटिलता वाले एल्गोरिदम के लिए उपयोग किया जाता है। ध्यान दें कि हम कई चीजों के बारे में बात नहीं कर रहे हैं जो यहां भिन्न हो सकती हैं: इंटरनेट की गति, हमारे कंप्यूटर की कम्प्यूटेशनल शक्ति, और इसी तरह। एल्गोरिथ्म की जटिलता का आकलन करते समय, इन कारकों पर विचार करने का कोई मतलब नहीं है - किसी भी घटना में, वे हमारे नियंत्रण से बाहर हैं। बिग ओ नोटेशन एल्गोरिथम की जटिलता को ही व्यक्त करता है, न कि "पर्यावरण" जिसमें यह चलता है। आइए हमारे उदाहरण के साथ जारी रखें। मान लीजिए कि हमें अंततः पता चलता है कि हमें कुल 800 टेराबाइट की फाइल भेजने की आवश्यकता है। बेशक, हम उन्हें इंटरनेट पर भेजकर अपना काम पूरा कर सकते हैं। बस एक समस्या है: मानक घरेलू डेटा संचरण दर (प्रति सेकंड 100 मेगाबिट्स) पर, इसमें लगभग 708 दिन लगेंगे। लगभग 2 वर्ष! : ओ हमारा एल्गोरिदम स्पष्ट रूप से यहां उपयुक्त नहीं है। हमें किसी और उपाय की जरूरत है! अप्रत्याशित रूप से, आईटी दिग्गज अमेज़न हमारे बचाव में आता है! अमेज़ॅन की स्नोमोबाइल सेवा हमें मोबाइल स्टोरेज में बड़ी मात्रा में डेटा अपलोड करने देती है और फिर इसे ट्रक द्वारा वांछित पते पर पहुंचाती है! तो, हमारे पास एक नया एल्गोरिदम है! "यदि आप 5000 मील की दूरी पर फ़ाइलों के रूप में जानकारी स्थानांतरित करना चाहते हैं और ऐसा करने में इंटरनेट के माध्यम से भेजने में 14 दिन से अधिक समय लगेगा, तो आपको डेटा को अमेज़ॅन ट्रक पर भेजना चाहिए।" हमने यहां मनमाने ढंग से 14 दिन चुने। मान लीजिए कि यह सबसे लंबी अवधि है जिसका हम इंतजार कर सकते हैं। आइए हमारे एल्गोरिदम का विश्लेषण करें। इसकी गति के बारे में क्या? यहां तक ​​कि अगर ट्रक केवल 50 मील प्रति घंटे की गति से यात्रा करता है, तो वह केवल 100 घंटों में 5000 मील की दूरी तय करेगा। यह चार दिनों से थोड़ा अधिक है! यह इंटरनेट पर डेटा भेजने के विकल्प से काफी बेहतर है। और इस एल्गोरिदम की जटिलता के बारे में क्या? क्या यह भी रैखिक है, अर्थात O(n)? नहीं, यह नहीं है। आखिरकार, ट्रक इस बात की परवाह नहीं करता है कि आप उसे कितना भारी लोड करते हैं - यह अभी भी लगभग उसी गति से चलेगा और समय पर पहुंचेगा। चाहे हमारे पास 800 टेराबाइट हों, या उससे 10 गुना, ट्रक अभी भी 5 दिनों के भीतर अपने गंतव्य तक पहुंच जाएगा। दूसरे शब्दों में, ट्रक-आधारित डेटा ट्रांसफर एल्गोरिथम में निरंतर जटिलता होती है. यहाँ, "स्थिर" का अर्थ है कि यह इनपुट डेटा के आकार पर निर्भर नहीं करता है। ट्रक में 1GB की फ्लैश ड्राइव रखो, यह 5 दिनों के भीतर आ जाएगी। 800 टेराबाइट डेटा वाले डिस्क में डालें, यह 5 दिनों के भीतर आ जाएगा। बिग ओ नोटेशन का उपयोग करते समय, निरंतर जटिलता को O(1) द्वारा निरूपित किया जाता है । हम O(n) और O(1) से परिचित हो गए हैं, तो अब प्रोग्रामिंग की दुनिया में और उदाहरण देखें :) मान लीजिए कि आपको 100 नंबरों की एक सरणी दी गई है, और कार्य उनमें से प्रत्येक को प्रदर्शित करना है सांत्वना। आप एक साधारण forलूप लिखते हैं जो इस कार्य को करता है

int[] numbers = new int[100];
// ...fill the array with numbers

for (int i: numbers) {
   System.out.println(i);
}

इस एल्गोरिदम की जटिलता क्या है? रैखिक, यानी ओ (एन)। प्रोग्राम द्वारा निष्पादित की जाने वाली कार्रवाइयों की संख्या इस बात पर निर्भर करती है कि उसे कितनी संख्याएँ दी गई हैं। यदि सरणी में 100 संख्याएँ हैं, तो 100 क्रियाएँ होंगी (स्क्रीन पर तार प्रदर्शित करने के लिए कथन)। यदि सरणी में 10,000 संख्याएँ हैं, तो 10,000 क्रियाएँ अवश्य की जानी चाहिए। क्या हमारे एल्गोरिदम को किसी भी तरह से सुधारा जा सकता है? नहीं। कोई बात नहीं, हमें कंसोल पर स्ट्रिंग प्रदर्शित करने के लिए एन को एरे से गुजरना होगा और एन स्टेटमेंट को निष्पादित करना होगा। एक और उदाहरण पर गौर कीजिए।

public static void main(String[] args) {

   LinkedList<Integer> numbers = new LinkedList<>();
   numbers.add(0, 20202);
   numbers.add(0, 123);
   numbers.add(0, 8283);
}

हमारे पास एक खाली है LinkedListजिसमें हम कई संख्याएँ सम्मिलित करते हैं। हमें अपने उदाहरण में एकल संख्या डालने की एल्गोरिथम जटिलता का मूल्यांकन करने की आवश्यकता है LinkedList, और यह सूची में तत्वों की संख्या पर कैसे निर्भर करता है। उत्तर O(1) है, अर्थात निरंतर जटिलता । क्यों? ध्यान दें कि हम प्रत्येक संख्या को सूची के आरंभ में सम्मिलित करते हैं। इसके अलावा, आपको याद होगा कि जब आप a में कोई संख्या डालते हैं LinkedList, तो तत्व कहीं नहीं जाते हैं। लिंक (या संदर्भ) अपडेट किए गए हैं (यदि आप भूल गए हैं कि लिंक्डलिस्ट कैसे काम करता है, तो हमारे पुराने पाठों में से एक को देखें )। यदि हमारी सूची में पहला नंबर है x, और हम सूची के सामने नंबर y डालते हैं, तो हमें बस इतना करना है:

x.previous  = y;
y.previous = null;
y.next = x;

जब हम लिंक्स को अपडेट करते हैं, तो हम इस बात की परवाह नहीं करते हैं कि पहले से कितनी संख्याएँ हैंLinkedList , चाहे एक अरब या एक अरब। एल्गोरिथम की जटिलता स्थिर है, अर्थात O(1)।

लघुगणकीय जटिलता

घबड़ाएं नहीं! :) यदि "लॉगरिदमिक" शब्द आपको इस पाठ को बंद करने और पढ़ना बंद करने के लिए प्रेरित करता है, तो बस कुछ मिनटों के लिए रुकें। यहां कोई पागल गणित नहीं होगा (इस तरह के बहुत सारे स्पष्टीकरण हैं), और हम प्रत्येक उदाहरण को अलग करेंगे। कल्पना कीजिए कि आपका काम 100 नंबरों की एक सरणी में एक विशिष्ट संख्या खोजना है। अधिक सटीक रूप से, आपको यह जांचने की आवश्यकता है कि यह वहां है या नहीं। जैसे ही आवश्यक संख्या मिल जाती है, खोज समाप्त हो जाती है, और आप कंसोल में निम्नलिखित प्रदर्शित करते हैं: "आवश्यक संख्या मिली! सरणी में इसकी अनुक्रमणिका = ...." आप इस कार्य को कैसे पूरा करेंगे? यहां समाधान स्पष्ट है: आपको सरणी के तत्वों पर एक-एक करके पुनरावृति करने की आवश्यकता है, पहले (या अंतिम से) से शुरू करें और जांचें कि क्या वर्तमान संख्या आपके द्वारा खोजे जा रहे मेल से मेल खाती है। इसलिए, क्रियाओं की संख्या सीधे सरणी में तत्वों की संख्या पर निर्भर करती है। यदि हमारे पास 100 संख्याएँ हैं, तो हमें संभावित रूप से 100 बार अगले तत्व पर जाने और 100 तुलनाएँ करने की आवश्यकता हो सकती है। यदि 1000 संख्याएँ हैं, तो 1000 तुलनाएँ हो सकती हैं। यह स्पष्ट रूप से रैखिक जटिलता है, अर्थातओ (एन) । और अब हम अपने उदाहरण में एक परिशोधन जोड़ेंगे: जिस सरणी में आपको संख्या खोजने की आवश्यकता है वह आरोही क्रम में क्रमबद्ध है । क्या यह हमारे कार्य के संबंध में कुछ बदलता है? हम अभी भी वांछित संख्या के लिए क्रूर-बल खोज कर सकते हैं। लेकिन वैकल्पिक रूप से, हम जाने-माने बाइनरी सर्च एल्गोरिदम का उपयोग कर सकते हैं ।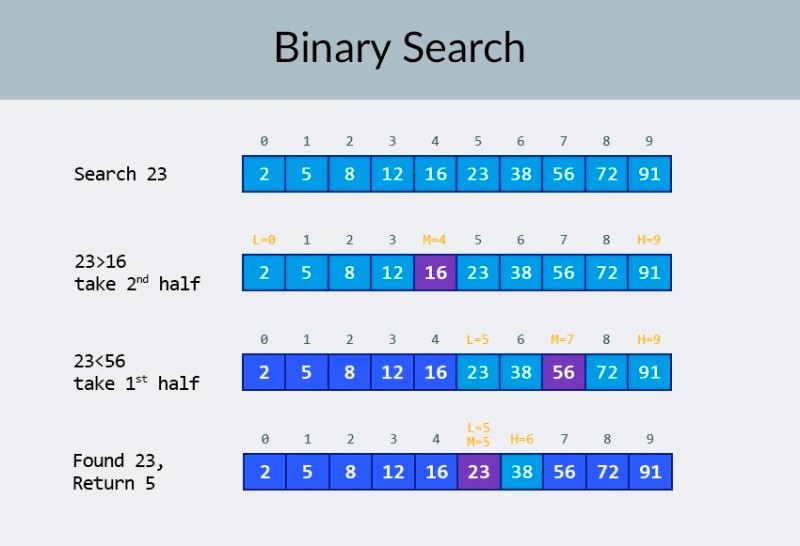 छवि में शीर्ष पंक्ति में, हम एक क्रमबद्ध सरणी देखते हैं। हमें इसमें 23 नंबर खोजने की जरूरत है। संख्याओं पर पुनरावृति करने के बजाय, हम केवल सरणी को 2 भागों में विभाजित करते हैं और सरणी में मध्य संख्या की जाँच करते हैं। सेल 4 में स्थित संख्या का पता लगाएं और इसे जांचें (छवि में दूसरी पंक्ति)। यह संख्या 16 है और हम 23 की तलाश कर रहे हैं। वर्तमान संख्या उससे कम है जिसे हम ढूंढ रहे हैं। इसका क्या मतलब है? यह मतलब है किपिछली सभी संख्याएँ (जो संख्या 16 से पहले स्थित हैं) को जाँचने की आवश्यकता नहीं है : हम जिस संख्या की तलाश कर रहे हैं, उससे कम होने की गारंटी है, क्योंकि हमारी सरणी क्रमबद्ध है! हम शेष 5 तत्वों के बीच खोज जारी रखते हैं। टिप्पणी:हमने केवल एक तुलना की है, लेकिन हमने संभावित विकल्पों में से आधे को पहले ही हटा दिया है। हमारे पास केवल 5 तत्व बचे हैं। हम अपने पिछले चरण को एक बार फिर से शेष उपश्रेणियों को आधे में विभाजित करके और फिर से मध्य तत्व (छवि में तीसरी पंक्ति) लेकर दोहराएंगे। संख्या 56 है, और यह उस संख्या से बड़ी है जिसकी हम तलाश कर रहे हैं। इसका क्या मतलब है? इसका मतलब है कि हमने अन्य 3 संभावनाओं को समाप्त कर दिया है: संख्या 56 और साथ ही इसके बाद की दो संख्याएँ (चूंकि वे 23 से अधिक होने की गारंटी हैं, क्योंकि सरणी क्रमबद्ध है)। हमारे पास जाँचने के लिए केवल 2 संख्याएँ बची हैं (छवि में अंतिम पंक्ति) - सरणी सूचकांक 5 और 6 के साथ संख्याएँ। हम उनमें से पहले की जाँच करते हैं, और पाते हैं कि हम क्या खोज रहे थे - संख्या 23! इसका सूचकांक 5 है! आइए अपने एल्गोरिदम के परिणामों को देखें, और फिर हम ' इसकी जटिलता का विश्लेषण करेंगे। वैसे, अब आप समझ गए हैं कि इसे बाइनरी सर्च क्यों कहा जाता है: यह डेटा को बार-बार आधे में विभाजित करने पर निर्भर करता है। परिणाम प्रभावशाली है! यदि हम संख्या खोजने के लिए एक रेखीय खोज का उपयोग करते हैं, तो हमें 10 तुलनाओं तक की आवश्यकता होगी, लेकिन एक द्विआधारी खोज के साथ, हमने केवल 3 के साथ कार्य पूरा किया! सबसे खराब स्थिति में, 4 तुलनाएँ होंगी (यदि अंतिम चरण में हम जो संख्या चाहते थे, वह पहली के बजाय शेष संभावनाओं में से दूसरी थी। तो इसकी जटिलता के बारे में क्या? यह एक बहुत ही दिलचस्प बिंदु है :) रैखिक खोज एल्गोरिदम (यानी, सरल पुनरावृत्ति) की तुलना में बाइनरी खोज एल्गोरिदम सरणी में तत्वों की संख्या पर बहुत कम निर्भर है। सरणी में 10 तत्वों के साथ , एक रैखिक खोज के लिए अधिकतम 10 तुलनाओं की आवश्यकता होगी, लेकिन एक बाइनरी खोज के लिए अधिकतम 4 तुलनाओं की आवश्यकता होगी। यह 2.5 के गुणक का अंतर है। लेकिन 1000 तत्वों की एक सरणी के लिए , एक रैखिक खोज के लिए 1000 तुलनाओं की आवश्यकता होगी, लेकिन एक बाइनरी खोज के लिए केवल 10 की आवश्यकता होगी ! अंतर अब 100 गुना है! टिप्पणी:सरणी में तत्वों की संख्या 100 गुना (10 से 1000 तक) बढ़ी है, लेकिन बाइनरी खोज के लिए आवश्यक तुलनाओं की संख्या में केवल 2.5 के कारक (4 से 10 तक) की वृद्धि हुई है। यदि हम 10,000 तत्व प्राप्त करते हैं , तो अंतर और भी प्रभावशाली होगा: रैखिक खोज के लिए 10,000 तुलनाएँ, और बाइनरी खोज के लिए कुल 14 तुलनाएँ । और फिर, यदि तत्वों की संख्या 1000 गुना (10 से 10000 तक) बढ़ जाती है, तो तुलना की संख्या केवल 3.5 (4 से 14 तक) के कारक से बढ़ जाती है। द्विआधारी खोज एल्गोरिदम की जटिलता लॉगरिदमिक है , या, यदि हम बड़े ओ नोटेशन का उपयोग करते हैं, ओ (लॉग एन). ऐसा क्यों कहा जाता है? लघुगणक घातांक के विपरीत है। द्विआधारी लघुगणक वह शक्ति है जिस तक संख्या 2 को एक संख्या प्राप्त करने के लिए उठाया जाना चाहिए। उदाहरण के लिए, हमारे पास 10,000 तत्व हैं जिन्हें हमें बाइनरी सर्च एल्गोरिदम का उपयोग करके खोजने की आवश्यकता है। 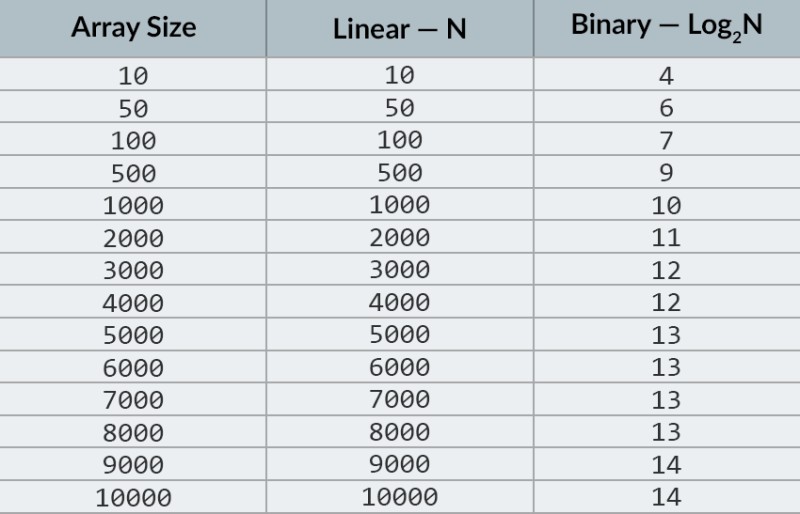वर्तमान में, आप यह जानने के लिए मानों की तालिका देख सकते हैं कि ऐसा करने के लिए अधिकतम 14 तुलनाओं की आवश्यकता होगी। लेकिन क्या होगा अगर किसी ने ऐसी तालिका प्रदान नहीं की है और आपको तुलना की सटीक अधिकतम संख्या की गणना करने की आवश्यकता है? आपको केवल एक सरल प्रश्न का उत्तर देने की आवश्यकता है: आपको संख्या 2 को बढ़ाने के लिए किस शक्ति की आवश्यकता है ताकि परिणाम जाँचे जाने वाले तत्वों की संख्या से अधिक या उसके बराबर हो? 10,000 के लिए, यह 14वीं शक्ति है। 2 से 13वीं शक्ति बहुत छोटी है (8192), लेकिन 2 से 14वीं शक्ति = 16384, और यह संख्या हमारी स्थिति को संतुष्ट करती है (यह सरणी में तत्वों की संख्या से अधिक या उसके बराबर है)। हमें लघुगणक मिला: 14। हमें कितनी तुलनाओं की आवश्यकता हो सकती है! :) एल्गोरिदम और एल्गोरिथम जटिलता एक पाठ में फिट होने के लिए बहुत व्यापक विषय है। लेकिन यह जानना बहुत महत्वपूर्ण है: कई नौकरी के साक्षात्कार में एल्गोरिदम से जुड़े प्रश्न शामिल होंगे। सिद्धांत के लिए, मैं आपके लिए कुछ पुस्तकों की अनुशंसा कर सकता हूं। आप " ग्रोकिंग एल्गोरिदम " से शुरू कर सकते हैं। इस पुस्तक के उदाहरण पायथन में लिखे गए हैं, लेकिन पुस्तक बहुत ही सरल भाषा और उदाहरणों का उपयोग करती है। नौसिखियों के लिए यह सबसे अच्छा विकल्प है और इससे भी बड़ी बात यह है कि यह बहुत बड़ा नहीं है। अधिक गंभीर पठन के बीच, हमारे पास रॉबर्ट लाफोर और रॉबर्ट सेडगेविक की पुस्तकें हैं. दोनों जावा में लिखे गए हैं, जिससे आपके लिए सीखना थोड़ा आसान हो जाएगा। आख़िरकार, आप इस भाषा से काफ़ी परिचित हैं! :) अच्छे गणित कौशल वाले छात्रों के लिए, थॉमस कॉर्मेन की किताब सबसे अच्छा विकल्प है । लेकिन अकेले सिद्धांत से आपका पेट नहीं भरेगा! ज्ञान != योग्यता । आप HackerRank और LeetCode पर एल्गोरिदम से जुड़ी समस्याओं को हल करने का अभ्यास कर सकते हैं । इन वेबसाइटों के कार्य अक्सर Google और Facebook पर साक्षात्कार के दौरान भी उपयोग किए जाते हैं, इसलिए आप निश्चित रूप से ऊब नहीं होंगे :) इस पाठ सामग्री को सुदृढ़ करने के लिए, मेरा सुझाव है कि आप YouTube पर बिग ओ नोटेशन के बारे में यह उत्कृष्ट वीडियो देखें। अगले पाठों में मिलते हैं! :)