Bună! Lecția de astăzi va fi puțin diferită de restul. Acesta va diferi prin faptul că este doar indirect legat de Java. Acestea fiind spuse, acest subiect este foarte important pentru fiecare programator. Vom vorbi despre algoritmi . Ce este un algoritm? În termeni simpli, este o secvență de acțiuni care trebuie finalizată pentru a obține rezultatul dorit . Folosim algoritmi des în viața de zi cu zi. De exemplu, în fiecare dimineață aveți o sarcină specifică: mergeți la școală sau la serviciu și, în același timp, fiți:
Îmbrăcat
Curat
hrănit
Ce algoritm vă permite să obțineți acest rezultat?
Treziți-vă folosind un ceas cu alarmă.
Fă un duș și spală-te.
Pregătiți micul dejun și niște cafea sau ceai.
Mânca.
Dacă nu ți-ai călcat hainele în seara precedentă, atunci călcă-le.
Îmbracă-te.
Ieși din casă.
Această secvență de acțiuni vă va permite cu siguranță să obțineți rezultatul dorit. În programare, lucrăm constant pentru a îndeplini sarcinile. O parte semnificativă a acestor sarcini poate fi efectuată folosind algoritmi care sunt deja cunoscuți. De exemplu, să presupunem că sarcina dvs. este următoarea: sortați o listă de 100 de nume într-o matrice . Această sarcină este destul de simplă, dar poate fi rezolvată în moduri diferite. Iată o soluție posibilă: algoritm pentru sortarea alfabetică a numelor:
Cumpărați sau descărcați ediția din 1961 a Webster's Third New International Dictionary.
Găsiți fiecare nume din lista noastră în acest dicționar.
Pe o bucată de hârtie, scrieți pagina dicționarului pe care se află numele.
Utilizați bucățile de hârtie pentru a sorta numele.
O astfel de succesiune de acțiuni ne va îndeplini sarcina? Da, cu siguranță va fi. Este eficienta aceasta solutie ? Cu greu. Aici ajungem la alte aspecte foarte importante ale algoritmilor: eficiența lor . Există mai multe moduri de a îndeplini această sarcină. Dar atât în programare, cât și în viața obișnuită, vrem să alegem cea mai eficientă cale. Dacă sarcina ta este să faci o bucată de pâine prăjită unsă cu unt, poți începe prin a semăna grâu și a mulge o vacă. Dar asta ar fi ineficientsoluție — va dura mult timp și va costa mulți bani. Vă puteți îndeplini sarcina simplă cumpărând pur și simplu pâine și unt. Deși vă permite să rezolvați problema, algoritmul care implică grâu și o vacă este prea complex pentru a fi folosit în practică. În programare, avem notație specială numită notație mare O pentru a evalua complexitatea algoritmilor. Big O face posibilă evaluarea cât de mult depinde timpul de execuție al unui algoritm de dimensiunea datelor de intrare . Să ne uităm la cel mai simplu exemplu: transferul de date. Imaginați-vă că trebuie să trimiteți unele informații sub forma unui fișier pe o distanță lungă (de exemplu, 5000 de mile). Ce algoritm ar fi cel mai eficient? Depinde de datele cu care lucrezi. De exemplu, să presupunem că avem un fișier audio care are 10 MB. În acest caz, cel mai eficient algoritm este trimiterea fișierului prin Internet. Nu putea dura mai mult de câteva minute! Să reformulam algoritmul nostru: „Dacă doriți să transferați informații sub formă de fișiere pe o distanță de 5000 de mile, ar trebui să trimiteți datele prin Internet”. Excelent. Acum hai să o analizăm. Ne îndeplinește sarcina?Ei bine, da, da. Dar ce putem spune despre complexitatea sa? Hmm, acum lucrurile devin mai interesante. Faptul este că algoritmul nostru este foarte dependent de datele de intrare, și anume de dimensiunea fișierelor. Dacă avem 10 megaocteți, atunci totul este în regulă. Dar dacă trebuie să trimitem 500 de megaocteți? 20 de gigaocteți? 500 terabytes? 30 de petabytes? Algoritmul nostru va înceta să funcționeze? Nu, toate aceste cantități de date pot fi într-adevăr transferate. Va dura mai mult? Da se va! Acum cunoaștem o caracteristică importantă a algoritmului nostru: cu cât este mai mare cantitatea de date de trimis, cu atât va dura mai mult pentru a rula algoritmul.. Dar am dori să avem o înțelegere mai precisă a acestei relații (între dimensiunea datelor de intrare și timpul necesar pentru a le trimite). În cazul nostru, complexitatea algoritmică este liniară . „Liniar” înseamnă că, pe măsură ce cantitatea de date de intrare crește, timpul necesar pentru a le trimite va crește aproximativ proporțional. Dacă cantitatea de date se dublează, atunci timpul necesar pentru a le trimite va fi de două ori mai mare. Dacă datele cresc de 10 ori, atunci timpul de transmisie va crește de 10 ori. Folosind notația mare O, complexitatea algoritmului nostru este exprimată ca O(n). Ar trebui să vă amintiți această notație pentru viitor - este întotdeauna folosită pentru algoritmi cu complexitate liniară. Rețineți că nu vorbim despre câteva lucruri care pot varia aici: viteza Internetului, puterea de calcul a computerului nostru și așa mai departe. Când evaluăm complexitatea unui algoritm, pur și simplu nu are sens să luăm în considerare acești factori - în orice caz, ei sunt în afara controlului nostru. Notația Big O exprimă complexitatea algoritmului în sine, nu „mediul” în care rulează. Să continuăm cu exemplul nostru. Să presupunem că în cele din urmă aflăm că trebuie să trimitem fișiere cu un total de 800 de terabytes. Desigur, ne putem îndeplini sarcina trimițându-le prin Internet. Există o singură problemă: la ratele standard de transmisie a datelor de uz casnic (100 megabiți pe secundă), va dura aproximativ 708 zile. Aproape 2 ani! :O Algoritmul nostru evident nu se potrivește bine aici. Avem nevoie de altă soluție! În mod neașteptat, gigantul IT Amazon vine în ajutorul nostru! Serviciul Amazon Snowmobile ne permite să încărcăm o cantitate mare de date în stocarea mobilă și apoi să le livrăm la adresa dorită cu camionul! Deci, avem un nou algoritm! „Dacă doriți să transferați informații sub formă de fișiere pe o distanță de 5.000 de mile și trimiterea lor prin internet ar dura mai mult de 14 zile, ar trebui să trimiteți datele pe un camion Amazon”. Am ales 14 zile în mod arbitrar aici. Să spunem că aceasta este cea mai lungă perioadă pe care o putem aștepta. Să analizăm algoritmul nostru. Dar viteza lui? Chiar dacă camionul circulă cu doar 50 mph, va parcurge 5000 de mile în doar 100 de ore. Este puțin peste patru zile! Aceasta este mult mai bună decât opțiunea de a trimite datele prin Internet. Și cum rămâne cu complexitatea acestui algoritm? Este și liniară, adică O(n)? Nu Nu este. La urma urmei, camionului nu-i pasă cât de greu îl încărcați - va conduce în continuare cam la aceeași viteză și va ajunge la timp. Indiferent dacă avem 800 terabytes sau de 10 ori mai mult, camionul va ajunge la destinație în 5 zile. Cu alte cuvinte, algoritmul de transfer de date bazat pe camion are o complexitate constantă. Aici, „constant” înseamnă că nu depinde de dimensiunea datelor de intrare. Pune o unitate flash de 1 GB în camion, aceasta va ajunge în 5 zile. Puneți în discuri care conțin 800 terabytes de date, vor ajunge în 5 zile. Când se folosește notația mare O, complexitatea constantă este notată cu O(1) . Ne-am familiarizat cu O(n) și O(1) , așa că acum să ne uităm la mai multe exemple din lumea programării :) Să presupunem că vi se oferă o matrice de 100 de numere și sarcina este să afișați fiecare dintre ele pe consola. Scrieți o forbuclă obișnuită care îndeplinește această sarcină
int[] numbers = new int[100];
// ...fill the array with numbers
for (int i: numbers) {
System.out.println(i);
}
Care este complexitatea acestui algoritm? Linear, adică O(n). Numărul de acțiuni pe care programul trebuie să le efectueze depinde de câte numere îi sunt transmise. Dacă există 100 de numere în matrice, vor exista 100 de acțiuni (instrucțiuni pentru a afișa șiruri pe ecran). Dacă există 10.000 de numere în matrice, atunci trebuie efectuate 10.000 de acțiuni. Algoritmul nostru poate fi îmbunătățit în vreun fel? Nu. Indiferent de ce, va trebui să facem N treceri prin matrice și să executăm N instrucțiuni pentru a afișa șiruri de caractere pe consolă. Luați în considerare un alt exemplu.
public static void main(String[] args) {
LinkedList<Integer> numbers = new LinkedList<>();
numbers.add(0, 20202);
numbers.add(0, 123);
numbers.add(0, 8283);
}
Avem un gol LinkedListîn care introducem mai multe numere. Trebuie să evaluăm complexitatea algoritmică a inserării unui singur număr în LinkedListexemplul nostru și modul în care aceasta depinde de numărul de elemente din listă. Răspunsul este O(1), adică complexitate constantă . De ce? Rețineți că inserăm fiecare număr la începutul listei. În plus, vă veți aminti că atunci când introduceți un număr într-un LinkedList, elementele nu se mișcă nicăieri. Legăturile (sau referințele) sunt actualizate (dacă ați uitat cum funcționează LinkedList, uitați-vă la una dintre vechile noastre lecții ). Dacă primul număr din lista noastră este x, și inserăm numărul y în partea de sus a listei, atunci tot ce trebuie să facem este următorul:
x.previous = y;
y.previous = null;
y.next = x;
Când actualizăm linkurile, nu ne interesează câte numere sunt deja înLinkedList , fie unul sau un miliard. Complexitatea algoritmului este constantă, adică O(1).
Complexitate logaritmică
Nu vă panicați! :) Dacă cuvântul „logaritmic” vă face să doriți să închideți această lecție și să nu mai citiți, țineți doar câteva minute. Nu va fi nicio matematică nebună aici (există o mulțime de explicații de acest fel în altă parte) și vom alege fiecare exemplu. Imaginează-ți că sarcina ta este să găsești un anumit număr într-o matrice de 100 de numere. Mai exact, trebuie să verificați dacă există sau nu. De îndată ce numărul necesar este găsit, căutarea se termină și veți afișa următoarele în consolă: "Numărul necesar a fost găsit! Indexul său în matrice = ...." Cum ați îndeplini această sarcină? Aici soluția este evidentă: trebuie să iterați unul câte unul peste elementele matricei, începând de la primul (sau de la ultimul) și să verificați dacă numărul curent se potrivește cu cel pe care îl căutați. În consecinţă, numărul de acțiuni depinde direct de numărul de elemente din matrice. Dacă avem 100 de numere, atunci ar putea fi necesar să mergem la următorul element de 100 de ori și să facem 100 de comparații. Dacă există 1000 de numere, atunci ar putea exista 1000 de comparații. Aceasta este în mod evident o complexitate liniară, adicăO(n) . Și acum vom adăuga o rafinare exemplului nostru: matricea în care trebuie să găsiți numărul este sortată în ordine crescătoare . Schimbă asta ceva în ceea ce privește sarcina noastră? Am putea efectua în continuare o căutare cu forță brută pentru numărul dorit. Dar, alternativ, am putea folosi binecunoscutul algoritm de căutare binar .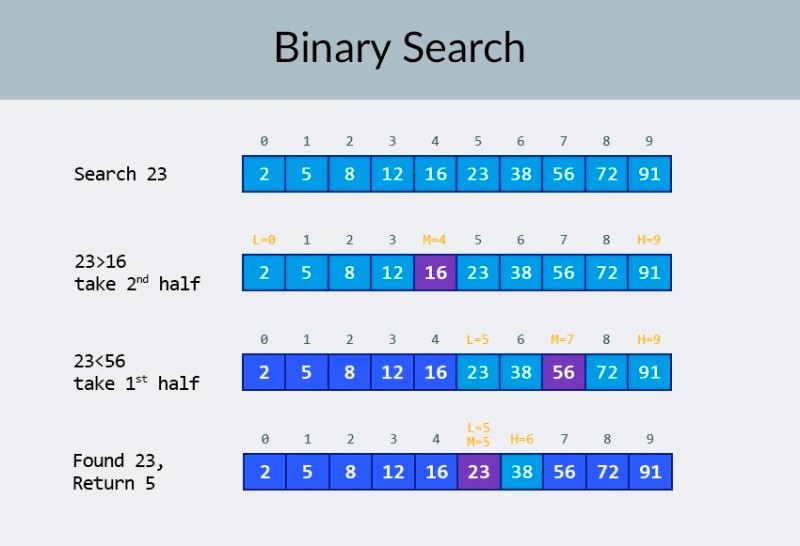 În rândul de sus al imaginii, vedem o matrice sortată. Trebuie să găsim numărul 23 în el. În loc să repetăm peste numere, pur și simplu împărțim matricea în 2 părți și verificăm numărul din mijloc din matrice. Găsiți numărul care se află în celula 4 și verificați-l (al doilea rând din imagine). Acest număr este 16, iar noi căutăm 23. Numărul actual este mai mic decât ceea ce căutăm. Ce înseamnă asta? Înseamnă cătoate numerele anterioare (cele situate înainte de numărul 16) nu trebuie verificate : este garantat că sunt mai mici decât cea pe care o căutăm, deoarece matricea noastră este sortată! Continuăm căutarea printre cele 5 elemente rămase. Notă:am efectuat o singură comparație, dar am eliminat deja jumătate dintre opțiunile posibile. Mai avem doar 5 elemente. Vom repeta pasul anterior împărțind încă o dată subbaryul rămas în jumătate și luând din nou elementul din mijloc (al treilea rând din imagine). Numărul este 56 și este mai mare decât cel pe care îl căutăm. Ce înseamnă asta? Înseamnă că am eliminat alte 3 posibilități: numărul 56 însuși precum și cele două numere de după el (deoarece sunt garantate a fi mai mari decât 23, deoarece tabloul este sortat). Mai avem de verificat doar 2 numere (ultimul rând din imagine) — numerele cu indici de matrice 5 și 6. Verificăm primul dintre ele și găsim ceea ce căutam — numărul 23! Indicele lui este 5! Să ne uităm la rezultatele algoritmului nostru, apoi vom" Îi voi analiza complexitatea. Apropo, acum înțelegeți de ce aceasta se numește căutare binară: se bazează pe împărțirea în mod repetat a datelor la jumătate. Rezultatul este impresionant! Dacă am folosi o căutare liniară pentru a căuta numărul, am avea nevoie de până la 10 comparații, dar cu o căutare binară, am îndeplinit sarcina doar cu 3! În cel mai rău caz, ar exista 4 comparații (dacă în ultimul pas numărul pe care l-am dorit ar fi a doua dintre posibilitățile rămase, mai degrabă decât prima. Deci, cum rămâne cu complexitatea lui? Acesta este un punct foarte interesant :) Algoritmul de căutare binar este mult mai puțin dependent de numărul de elemente din matrice decât algoritmul de căutare liniară (adică o iterație simplă). Cu 10 elemente în matrice, o căutare liniară va avea nevoie de maximum 10 comparații, dar o căutare binară va avea nevoie de maximum 4 comparații. Aceasta este o diferență cu un factor de 2,5. Dar pentru o matrice de 1000 de elemente , o căutare liniară va avea nevoie de până la 1000 de comparații, dar o căutare binară ar necesita doar 10 ! Diferența este acum de 100 de ori! Notă:numărul de elemente din matrice a crescut de 100 de ori (de la 10 la 1000), dar numărul de comparații necesare pentru o căutare binară a crescut cu un factor de doar 2,5 (de la 4 la 10). Dacă ajungem la 10.000 de elemente , diferența va fi și mai impresionantă: 10.000 de comparații pentru căutare liniară și un total de 14 comparații pentru căutare binară. Și din nou, dacă numărul de elemente crește de 1000 de ori (de la 10 la 10000), atunci numărul de comparații crește doar cu un factor de 3,5 (de la 4 la 14). Complexitatea algoritmului de căutare binar este logaritmică sau, dacă folosim notația mare O, O(log n). De ce se numește așa? Logaritmul este ca opusul exponențiației. Logaritmul binar este puterea la care trebuie ridicat numărul 2 pentru a obține un număr. De exemplu, avem 10.000 de elemente pe care trebuie să le căutăm folosind algoritmul de căutare binar. În prezent, puteți să vă uitați la tabelul de valori pentru a ști că pentru a face acest lucru va fi nevoie de maximum 14 comparații. Dar dacă nimeni nu a furnizat un astfel de tabel și trebuie să calculați numărul maxim exact de comparații? Trebuie doar să răspunzi la o întrebare simplă: la ce putere trebuie să ridici numărul 2, astfel încât rezultatul să fie mai mare sau egal cu numărul de elemente de verificat? Pentru 10.000, este a 14-a putere. Puterea 2 la a 13-a este prea mică (8192), dar puterea 2 la a 14-a = 16384, iar acest număr ne satisface condiția (este mai mare sau egal cu numărul de elemente din tablou). Am găsit logaritmul: 14. De câte comparații am putea avea nevoie! :) Algoritmii și complexitatea algoritmică este un subiect prea larg pentru a se încadra într-o lecție. Dar să știi că este foarte important: multe interviuri de angajare vor implica întrebări care implică algoritmi. Ca teorie, vă pot recomanda câteva cărți. Puteți începe cu „ Algoritmi Grokking ”. Exemplele din această carte sunt scrise în Python, dar cartea folosește un limbaj și exemple foarte simple. Este cea mai bună opțiune pentru un începător și, mai mult, nu este foarte mare. Printre lecturi mai serioase, avem cărți de Robert Lafore și Robert Sedgewick. Ambele sunt scrise în Java, ceea ce vă va ușura puțin învățarea. La urma urmei, ești destul de familiar cu această limbă! :) Pentru elevii cu abilități bune de matematică, cea mai bună opțiune este cartea lui Thomas Cormen . Dar teoria singură nu îți va umple burta! Cunoștințe != Abilitate . Puteți exersa rezolvarea problemelor care implică algoritmi pe HackerRank și LeetCode . Sarcinile de pe aceste site-uri sunt adesea folosite chiar și în timpul interviurilor la Google și Facebook, așa că cu siguranță nu vă veți plictisi :) Pentru a consolida acest material de lecție, vă recomand să urmăriți acest videoclip excelent despre notația O mare pe YouTube. Ne vedem la următoarele lecții! :)
Acestea fiind spuse, acest subiect este foarte important pentru fiecare programator. Vom vorbi despre algoritmi . Ce este un algoritm? În termeni simpli, este o secvență de acțiuni care trebuie finalizată pentru a obține rezultatul dorit . Folosim algoritmi des în viața de zi cu zi. De exemplu, în fiecare dimineață aveți o sarcină specifică: mergeți la școală sau la serviciu și, în același timp, fiți:
În acest caz, cel mai eficient algoritm este trimiterea fișierului prin Internet. Nu putea dura mai mult de câteva minute! Să reformulam algoritmul nostru: „Dacă doriți să transferați informații sub formă de fișiere pe o distanță de 5000 de mile, ar trebui să trimiteți datele prin Internet”. Excelent. Acum hai să o analizăm. Ne îndeplinește sarcina?Ei bine, da, da. Dar ce putem spune despre complexitatea sa? Hmm, acum lucrurile devin mai interesante. Faptul este că algoritmul nostru este foarte dependent de datele de intrare, și anume de dimensiunea fișierelor. Dacă avem 10 megaocteți, atunci totul este în regulă. Dar dacă trebuie să trimitem 500 de megaocteți? 20 de gigaocteți? 500 terabytes? 30 de petabytes? Algoritmul nostru va înceta să funcționeze? Nu, toate aceste cantități de date pot fi într-adevăr transferate. Va dura mai mult? Da se va! Acum cunoaștem o caracteristică importantă a algoritmului nostru: cu cât este mai mare cantitatea de date de trimis, cu atât va dura mai mult pentru a rula algoritmul.. Dar am dori să avem o înțelegere mai precisă a acestei relații (între dimensiunea datelor de intrare și timpul necesar pentru a le trimite). În cazul nostru, complexitatea algoritmică este liniară . „Liniar” înseamnă că, pe măsură ce cantitatea de date de intrare crește, timpul necesar pentru a le trimite va crește aproximativ proporțional. Dacă cantitatea de date se dublează, atunci timpul necesar pentru a le trimite va fi de două ori mai mare. Dacă datele cresc de 10 ori, atunci timpul de transmisie va crește de 10 ori. Folosind notația mare O, complexitatea algoritmului nostru este exprimată ca O(n). Ar trebui să vă amintiți această notație pentru viitor - este întotdeauna folosită pentru algoritmi cu complexitate liniară. Rețineți că nu vorbim despre câteva lucruri care pot varia aici: viteza Internetului, puterea de calcul a computerului nostru și așa mai departe. Când evaluăm complexitatea unui algoritm, pur și simplu nu are sens să luăm în considerare acești factori - în orice caz, ei sunt în afara controlului nostru. Notația Big O exprimă complexitatea algoritmului în sine, nu „mediul” în care rulează. Să continuăm cu exemplul nostru. Să presupunem că în cele din urmă aflăm că trebuie să trimitem fișiere cu un total de 800 de terabytes. Desigur, ne putem îndeplini sarcina trimițându-le prin Internet. Există o singură problemă: la ratele standard de transmisie a datelor de uz casnic (100 megabiți pe secundă), va dura aproximativ 708 zile. Aproape 2 ani! :O Algoritmul nostru evident nu se potrivește bine aici. Avem nevoie de altă soluție! În mod neașteptat, gigantul IT Amazon vine în ajutorul nostru! Serviciul Amazon Snowmobile ne permite să încărcăm o cantitate mare de date în stocarea mobilă și apoi să le livrăm la adresa dorită cu camionul! 
Deci, avem un nou algoritm! „Dacă doriți să transferați informații sub formă de fișiere pe o distanță de 5.000 de mile și trimiterea lor prin internet ar dura mai mult de 14 zile, ar trebui să trimiteți datele pe un camion Amazon”. Am ales 14 zile în mod arbitrar aici. Să spunem că aceasta este cea mai lungă perioadă pe care o putem aștepta. Să analizăm algoritmul nostru. Dar viteza lui? Chiar dacă camionul circulă cu doar 50 mph, va parcurge 5000 de mile în doar 100 de ore. Este puțin peste patru zile! Aceasta este mult mai bună decât opțiunea de a trimite datele prin Internet. Și cum rămâne cu complexitatea acestui algoritm? Este și liniară, adică O(n)? Nu Nu este. La urma urmei, camionului nu-i pasă cât de greu îl încărcați - va conduce în continuare cam la aceeași viteză și va ajunge la timp. Indiferent dacă avem 800 terabytes sau de 10 ori mai mult, camionul va ajunge la destinație în 5 zile. Cu alte cuvinte, algoritmul de transfer de date bazat pe camion are o complexitate constantă. Aici, „constant” înseamnă că nu depinde de dimensiunea datelor de intrare. Pune o unitate flash de 1 GB în camion, aceasta va ajunge în 5 zile. Puneți în discuri care conțin 800 terabytes de date, vor ajunge în 5 zile. Când se folosește notația mare O, complexitatea constantă este notată cu O(1) . Ne-am familiarizat cu O(n) și O(1) , așa că acum să ne uităm la mai multe exemple din lumea programării :) Să presupunem că vi se oferă o matrice de 100 de numere și sarcina este să afișați fiecare dintre ele pe consola. Scrieți o 
În rândul de sus al imaginii, vedem o matrice sortată. Trebuie să găsim numărul 23 în el. În loc să repetăm peste numere, pur și simplu împărțim matricea în 2 părți și verificăm numărul din mijloc din matrice. Găsiți numărul care se află în celula 4 și verificați-l (al doilea rând din imagine). Acest număr este 16, iar noi căutăm 23. Numărul actual este mai mic decât ceea ce căutăm. Ce înseamnă asta? Înseamnă cătoate numerele anterioare (cele situate înainte de numărul 16) nu trebuie verificate : este garantat că sunt mai mici decât cea pe care o căutăm, deoarece matricea noastră este sortată! Continuăm căutarea printre cele 5 elemente rămase. Notă:am efectuat o singură comparație, dar am eliminat deja jumătate dintre opțiunile posibile. Mai avem doar 5 elemente. Vom repeta pasul anterior împărțind încă o dată subbaryul rămas în jumătate și luând din nou elementul din mijloc (al treilea rând din imagine). Numărul este 56 și este mai mare decât cel pe care îl căutăm. Ce înseamnă asta? Înseamnă că am eliminat alte 3 posibilități: numărul 56 însuși precum și cele două numere de după el (deoarece sunt garantate a fi mai mari decât 23, deoarece tabloul este sortat). Mai avem de verificat doar 2 numere (ultimul rând din imagine) — numerele cu indici de matrice 5 și 6. Verificăm primul dintre ele și găsim ceea ce căutam — numărul 23! Indicele lui este 5! Să ne uităm la rezultatele algoritmului nostru, apoi vom" Îi voi analiza complexitatea. Apropo, acum înțelegeți de ce aceasta se numește căutare binară: se bazează pe împărțirea în mod repetat a datelor la jumătate. Rezultatul este impresionant! Dacă am folosi o căutare liniară pentru a căuta numărul, am avea nevoie de până la 10 comparații, dar cu o căutare binară, am îndeplinit sarcina doar cu 3! În cel mai rău caz, ar exista 4 comparații (dacă în ultimul pas numărul pe care l-am dorit ar fi a doua dintre posibilitățile rămase, mai degrabă decât prima. Deci, cum rămâne cu complexitatea lui? Acesta este un punct foarte interesant :) Algoritmul de căutare binar este mult mai puțin dependent de numărul de elemente din matrice decât algoritmul de căutare liniară (adică o iterație simplă). Cu 10 elemente în matrice, o căutare liniară va avea nevoie de maximum 10 comparații, dar o căutare binară va avea nevoie de maximum 4 comparații. Aceasta este o diferență cu un factor de 2,5. Dar pentru o matrice de 1000 de elemente , o căutare liniară va avea nevoie de până la 1000 de comparații, dar o căutare binară ar necesita doar 10 ! Diferența este acum de 100 de ori! Notă:numărul de elemente din matrice a crescut de 100 de ori (de la 10 la 1000), dar numărul de comparații necesare pentru o căutare binară a crescut cu un factor de doar 2,5 (de la 4 la 10). Dacă ajungem la 10.000 de elemente , diferența va fi și mai impresionantă: 10.000 de comparații pentru căutare liniară și un total de 14 comparații pentru căutare binară. Și din nou, dacă numărul de elemente crește de 1000 de ori (de la 10 la 10000), atunci numărul de comparații crește doar cu un factor de 3,5 (de la 4 la 14). Complexitatea algoritmului de căutare binar este logaritmică sau, dacă folosim notația mare O, O(log n). De ce se numește așa? Logaritmul este ca opusul exponențiației. Logaritmul binar este puterea la care trebuie ridicat numărul 2 pentru a obține un număr. De exemplu, avem 10.000 de elemente pe care trebuie să le căutăm folosind algoritmul de căutare binar. 
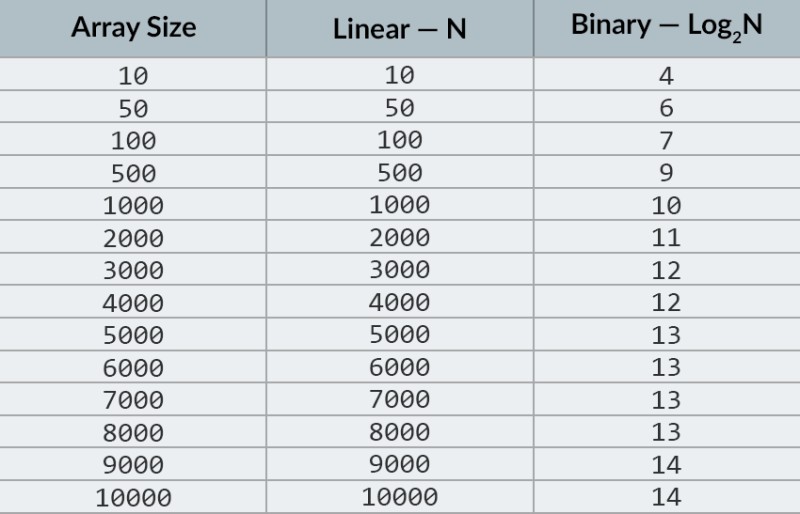În prezent, puteți să vă uitați la tabelul de valori pentru a ști că pentru a face acest lucru va fi nevoie de maximum 14 comparații. Dar dacă nimeni nu a furnizat un astfel de tabel și trebuie să calculați numărul maxim exact de comparații? Trebuie doar să răspunzi la o întrebare simplă: la ce putere trebuie să ridici numărul 2, astfel încât rezultatul să fie mai mare sau egal cu numărul de elemente de verificat? Pentru 10.000, este a 14-a putere. Puterea 2 la a 13-a este prea mică (8192), dar puterea 2 la a 14-a = 16384, iar acest număr ne satisface condiția (este mai mare sau egal cu numărul de elemente din tablou). Am găsit logaritmul: 14. De câte comparații am putea avea nevoie! :) Algoritmii și complexitatea algoritmică este un subiect prea larg pentru a se încadra într-o lecție. Dar să știi că este foarte important: multe interviuri de angajare vor implica întrebări care implică algoritmi. Ca teorie, vă pot recomanda câteva cărți. Puteți începe cu „ Algoritmi Grokking ”. Exemplele din această carte sunt scrise în Python, dar cartea folosește un limbaj și exemple foarte simple. Este cea mai bună opțiune pentru un începător și, mai mult, nu este foarte mare. Printre lecturi mai serioase, avem cărți de Robert Lafore și Robert Sedgewick. Ambele sunt scrise în Java, ceea ce vă va ușura puțin învățarea. La urma urmei, ești destul de familiar cu această limbă! :) Pentru elevii cu abilități bune de matematică, cea mai bună opțiune este cartea lui Thomas Cormen . Dar teoria singură nu îți va umple burta! Cunoștințe != Abilitate . Puteți exersa rezolvarea problemelor care implică algoritmi pe HackerRank și LeetCode . Sarcinile de pe aceste site-uri sunt adesea folosite chiar și în timpul interviurilor la Google și Facebook, așa că cu siguranță nu vă veți plictisi :) Pentru a consolida acest material de lecție, vă recomand să urmăriți acest videoclip excelent despre notația O mare pe YouTube. Ne vedem la următoarele lecții! :)
GO TO FULL VERSION