¡Hola! La lección de hoy será ligeramente diferente del resto. Diferirá en que solo está indirectamente relacionado con Java. Dicho esto, este tema es muy importante para todo programador. Vamos a hablar de algoritmos . ¿Qué es un algoritmo? En términos simples, es una secuencia de acciones que deben completarse para lograr un resultado deseado . Usamos algoritmos a menudo en la vida cotidiana. Por ejemplo, cada mañana tienes una tarea específica: ir a la escuela o al trabajo, y al mismo tiempo ser:
vestido
Limpio
alimentado
¿ Qué algoritmo te permite lograr este resultado?
Despierta usando un despertador.
Dúchate y lávate.
Haz el desayuno y un poco de café o té.
Comer.
Si no planchó su ropa la noche anterior, plánchela.
Vestirse.
Sal de la casa.
Esta secuencia de acciones definitivamente le permitirá obtener el resultado deseado. En programación, estamos trabajando constantemente para completar tareas. Una parte importante de estas tareas se puede realizar utilizando algoritmos que ya se conocen. Por ejemplo, suponga que su tarea es esta: ordenar una lista de 100 nombres en una matriz . Esta tarea es bastante simple, pero se puede resolver de diferentes maneras. Aquí hay una posible solución: Algoritmo para ordenar nombres alfabéticamente:
Compre o descargue la edición de 1961 del Tercer Nuevo Diccionario Internacional de Webster.
Encuentra todos los nombres de nuestra lista en este diccionario.
En una hoja de papel, escriba la página del diccionario en la que se encuentra el nombre.
Usa los pedazos de papel para ordenar los nombres.
¿Tal secuencia de acciones cumplirá nuestra tarea? Sí, ciertamente lo hará. ¿Es esta solución eficiente ? Difícilmente. Aquí llegamos a otro aspecto muy importante de los algoritmos: su eficiencia . Hay varias formas de realizar esta tarea. Pero tanto en la programación como en la vida cotidiana, queremos elegir la forma más eficiente. Si tu tarea es hacer una tostada con mantequilla, podrías empezar sembrando trigo y ordeñando una vaca. Pero eso sería ineficiente.solución: llevará mucho tiempo y costará mucho dinero. Puede realizar su tarea simple simplemente comprando pan y mantequilla. Aunque te permite resolver el problema, el algoritmo que involucra trigo y una vaca es demasiado complejo para usarlo en la práctica. En programación, tenemos una notación especial llamada notación O grande para evaluar la complejidad de los algoritmos. Big O permite evaluar cuánto depende el tiempo de ejecución de un algoritmo del tamaño de los datos de entrada . Veamos el ejemplo más simple: la transferencia de datos. Imagine que necesita enviar información en forma de archivo a larga distancia (por ejemplo, 5000 millas). ¿Qué algoritmo sería el más eficiente? Depende de los datos con los que estés trabajando. Por ejemplo, supongamos que tenemos un archivo de audio de 10 MB. En este caso, el algoritmo más eficiente es enviar el archivo a través de Internet. ¡No podría tomar más de un par de minutos! Repitamos nuestro algoritmo: "Si desea transferir información en forma de archivos a una distancia de 5000 millas, debe enviar los datos a través de Internet". Excelente. Ahora vamos a analizarlo. ¿Cumple con nuestra tarea?Bueno, sí, lo hace. Pero, ¿qué podemos decir de su complejidad? Hmm, ahora las cosas se están poniendo más interesantes. El hecho es que nuestro algoritmo depende mucho de los datos de entrada, es decir, del tamaño de los archivos. Si tenemos 10 megas, entonces todo está bien. Pero, ¿y si necesitamos enviar 500 megas? 20 gigas? 500 terabytes? 30 petabytes? ¿Dejará de funcionar nuestro algoritmo? No, todas estas cantidades de datos sí se pueden transferir. ¿Tomará más tiempo? ¡Sí, lo hará! Ahora conocemos una característica importante de nuestro algoritmo: cuanto mayor sea la cantidad de datos a enviar, más tiempo llevará ejecutar el algoritmo.. Pero nos gustaría tener una comprensión más precisa de esta relación (entre el tamaño de los datos de entrada y el tiempo necesario para enviarlos). En nuestro caso, la complejidad algorítmica es lineal . "Lineal" significa que a medida que aumenta la cantidad de datos de entrada, el tiempo que se tarda en enviarlos aumentará de forma aproximadamente proporcional. Si la cantidad de datos se duplica, el tiempo necesario para enviarlos será el doble. Si los datos aumentan 10 veces, el tiempo de transmisión aumentará 10 veces. Usando la notación O grande, la complejidad de nuestro algoritmo se expresa como O(n). Debe recordar esta notación para el futuro: siempre se usa para algoritmos con complejidad lineal. Tenga en cuenta que no estamos hablando de varias cosas que pueden variar aquí: la velocidad de Internet, la potencia de cómputo de nuestra computadora, etc. Al evaluar la complejidad de un algoritmo, simplemente no tiene sentido considerar estos factores; en cualquier caso, están fuera de nuestro control. La notación Big O expresa la complejidad del algoritmo en sí, no el "entorno" en el que se ejecuta. Sigamos con nuestro ejemplo. Supongamos que finalmente nos enteramos de que necesitamos enviar archivos por un total de 800 terabytes. Por supuesto, podemos realizar nuestra tarea enviándolos a través de Internet. Solo hay un problema: a velocidades de transmisión de datos domésticas estándar (100 megabits por segundo), tardará aproximadamente 708 días. ¡Casi 2 años! :O Nuestro algoritmo obviamente no encaja bien aquí. ¡Necesitamos otra solución! ¡Inesperadamente, el gigante de TI Amazon viene a rescatarnos! El servicio Snowmobile de Amazon nos permite cargar una gran cantidad de datos en el almacenamiento móvil y luego enviarlos a la dirección deseada por camión. Entonces, ¡tenemos un nuevo algoritmo! "Si desea transferir información en forma de archivos a una distancia de 5000 millas y hacerlo tardaría más de 14 días en enviarse a través de Internet, debe enviar los datos en un camión de Amazon". Elegimos 14 días arbitrariamente aquí. Digamos que este es el período más largo que podemos esperar. Analicemos nuestro algoritmo. ¿Qué pasa con su velocidad? Incluso si el camión viaja a solo 50 mph, cubrirá 5000 millas en solo 100 horas. ¡Esto es un poco más de cuatro días! Esto es mucho mejor que la opción de enviar los datos a través de Internet. ¿Y qué hay de la complejidad de este algoritmo? ¿Es también lineal, es decir, O(n)? No, no es. Después de todo, al camión no le importa qué tan pesado lo cargues, seguirá conduciendo aproximadamente a la misma velocidad y llegará a tiempo. Ya sea que tengamos 800 terabytes o 10 veces más, el camión aún llegará a su destino en 5 días. En otras palabras, el algoritmo de transferencia de datos basado en camiones tiene una complejidad constante. Aquí, "constante" significa que no depende del tamaño de los datos de entrada. Coloque una unidad flash de 1GB en el camión, llegará dentro de los 5 días. Coloque discos que contengan 800 terabytes de datos, llegará dentro de los 5 días. Cuando se usa la notación O grande, la complejidad constante se denota por O(1) . Nos hemos familiarizado con O(n) y O(1) , así que ahora veamos más ejemplos en el mundo de la programación :) Suponga que tiene una matriz de 100 números y la tarea es mostrar cada uno de ellos en la consola. Escribes un forbucle ordinario que realiza esta tarea.
int[] numbers = new int[100];
// ...fill the array with numbers
for (int i: numbers) {
System.out.println(i);
}
¿Cuál es la complejidad de este algoritmo? Lineal, es decir O(n). El número de acciones que debe realizar el programa depende de cuántos números se le pasen. Si hay 100 números en la matriz, habrá 100 acciones (instrucciones para mostrar cadenas en la pantalla). Si hay 10.000 números en la matriz, se deben realizar 10.000 acciones. ¿Se puede mejorar nuestro algoritmo de alguna manera? No. Pase lo que pase, tendremos que hacer N pases a través de la matriz y ejecutar N declaraciones para mostrar cadenas en la consola. Considere otro ejemplo.
public static void main(String[] args) {
LinkedList<Integer> numbers = new LinkedList<>();
numbers.add(0, 20202);
numbers.add(0, 123);
numbers.add(0, 8283);
}
Tenemos un vacío LinkedListen el que insertamos varios números. Necesitamos evaluar la complejidad algorítmica de insertar un solo número en LinkedListnuestro ejemplo, y cómo depende de la cantidad de elementos en la lista. La respuesta es O(1), es decir, complejidad constante . ¿Por qué? Tenga en cuenta que insertamos cada número al principio de la lista. Además, recordará que cuando inserta un número en un LinkedList, los elementos no se mueven a ningún lado. Los enlaces (o referencias) se actualizan (si olvidaste cómo funciona LinkedList, mira una de nuestras lecciones antiguas ). Si el primer número en nuestra lista es xe insertamos el número y al principio de la lista, todo lo que tenemos que hacer es esto:
x.previous = y;
y.previous = null;
y.next = x;
Cuando actualizamos los enlaces, no nos importa cuántos números ya hay en elLinkedList , si uno o mil millones. La complejidad del algoritmo es constante, es decir, O(1).
Complejidad logarítmica
¡No entrar en pánico! :) Si la palabra "logarítmico" le da ganas de cerrar esta lección y dejar de leer, espere un par de minutos. No habrá matemáticas locas aquí (hay muchas explicaciones como esa en otros lugares), y seleccionaremos cada ejemplo. Imagina que tu tarea es encontrar un número específico en una matriz de 100 números. Más precisamente, debe verificar si está allí o no. Tan pronto como se encuentra el número requerido, la búsqueda finaliza y muestra lo siguiente en la consola: "¡Se encontró el número requerido! Su índice en la matriz = ..." ¿Cómo realizaría esta tarea? Aquí la solución es obvia: debe iterar sobre los elementos de la matriz uno por uno, comenzando desde el primero (o desde el último) y verificar si el número actual coincide con el que está buscando. Respectivamente, el número de acciones depende directamente del número de elementos en la matriz. Si tenemos 100 números, potencialmente podríamos necesitar ir al siguiente elemento 100 veces y realizar 100 comparaciones. Si hay 1000 números, entonces podría haber 1000 comparaciones. Esto es obviamente complejidad lineal, es decirO(n) . Y ahora agregaremos un refinamiento a nuestro ejemplo: la matriz donde necesita encontrar el número está ordenada en orden ascendente . ¿Cambia esto algo con respecto a nuestra tarea? Todavía podríamos realizar una búsqueda de fuerza bruta para el número deseado. Pero alternativamente, podríamos utilizar el conocido algoritmo de búsqueda binaria .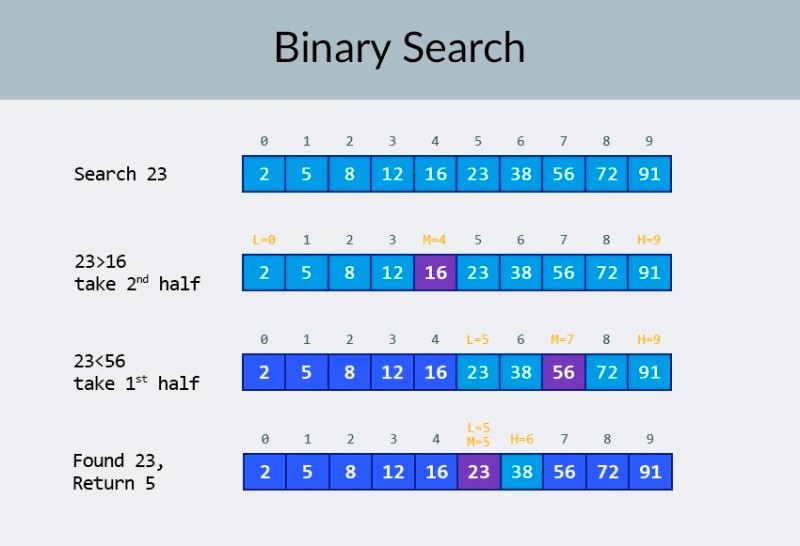 En la fila superior de la imagen, vemos una matriz ordenada. Necesitamos encontrar el número 23 en él. En lugar de iterar sobre los números, simplemente dividimos la matriz en 2 partes y verificamos el número del medio en la matriz. Encuentra el número que se encuentra en la celda 4 y compruébalo (segunda fila en la imagen). Este número es 16 y estamos buscando 23. El número actual es menor que lo que estamos buscando. ¿Qué significa eso? Esto significa quetodos los números anteriores (aquellos ubicados antes del número 16) no necesitan ser verificados : ¡se garantiza que son menores que el que estamos buscando, porque nuestra matriz está ordenada! Continuamos la búsqueda entre los 5 elementos restantes. Nota:hemos realizado una sola comparación, pero ya hemos eliminado la mitad de las opciones posibles. Solo nos quedan 5 elementos. Repetiremos nuestro paso anterior dividiendo una vez más el subarreglo restante por la mitad y tomando nuevamente el elemento del medio (la tercera fila en la imagen). El número es 56 y es más grande que el que estamos buscando. ¿Qué significa eso? Significa que hemos eliminado otras 3 posibilidades: el propio número 56 y los dos números que le siguen (ya que se garantiza que son mayores que 23, porque la matriz está ordenada). Solo nos quedan 2 números para verificar (la última fila en la imagen): los números con índices de matriz 5 y 6. Verificamos el primero de ellos y encontramos lo que estábamos buscando: ¡el número 23! ¡Su índice es 5! Veamos los resultados de nuestro algoritmo y luego Analizaré su complejidad. Por cierto, ahora entiendes por qué esto se llama búsqueda binaria: se basa en dividir repetidamente los datos por la mitad. ¡El resultado es impresionante! Si usáramos una búsqueda lineal para buscar el número, necesitaríamos hasta 10 comparaciones, pero con una búsqueda binaria, ¡logramos la tarea con solo 3! En el peor de los casos, habría 4 comparaciones (si en el último paso el número que queríamos fuera la segunda de las posibilidades restantes, en lugar de la primera. Entonces, ¿qué hay de su complejidad? Este es un punto muy interesante :) El algoritmo de búsqueda binaria depende mucho menos del número de elementos en la matriz que el algoritmo de búsqueda lineal (es decir, iteración simple). Con 10 elementos en la matriz, una búsqueda lineal necesitará un máximo de 10 comparaciones, pero una búsqueda binaria necesitará un máximo de 4 comparaciones. Esa es una diferencia por un factor de 2.5. Pero para una matriz de 1000 elementos , una búsqueda lineal necesitará hasta 1000 comparaciones, ¡pero una búsqueda binaria solo requerirá 10 ! ¡La diferencia ahora es 100 veces mayor! Nota:el número de elementos en la matriz ha aumentado 100 veces (de 10 a 1000), pero el número de comparaciones requeridas para una búsqueda binaria ha aumentado por un factor de solo 2,5 (de 4 a 10). Si llegamos a 10.000 elementos , la diferencia será aún más impresionante: 10.000 comparaciones para búsqueda lineal, y un total de 14 comparaciones para búsqueda binaria. Y nuevamente, si la cantidad de elementos aumenta 1000 veces (de 10 a 10000), entonces la cantidad de comparaciones aumenta en un factor de solo 3.5 (de 4 a 14). La complejidad del algoritmo de búsqueda binaria es logarítmica o, si usamos la notación O grande, O(log n). ¿Por qué se llama así? El logaritmo es como el opuesto de la exponenciación. El logaritmo binario es la potencia a la que se debe elevar el número 2 para obtener un número. Por ejemplo, tenemos 10.000 elementos que necesitamos buscar usando el algoritmo de búsqueda binaria. Actualmente, puede mirar la tabla de valores para saber que hacer esto requerirá un máximo de 14 comparaciones. Pero, ¿qué sucede si nadie ha proporcionado una tabla de este tipo y necesita calcular el número máximo exacto de comparaciones? Solo necesita responder una pregunta simple: ¿ a qué potencia necesita elevar el número 2 para que el resultado sea mayor o igual que la cantidad de elementos a verificar? Por 10.000, es la potencia 14. 2 a la potencia 13 es demasiado pequeño (8192), pero 2 a la potencia 14 = 16384, y este número satisface nuestra condición (es mayor o igual que el número de elementos en la matriz). Encontramos el logaritmo: 14. ¡Esas son las comparaciones que podríamos necesitar! :) Los algoritmos y la complejidad algorítmica es un tema demasiado amplio para caber en una lección. Pero saberlo es muy importante: muchas entrevistas de trabajo involucrarán preguntas que involucran algoritmos. En teoría, puedo recomendarte algunos libros. Puede comenzar con " Algoritmos de Grokking ". Los ejemplos de este libro están escritos en Python, pero el libro utiliza un lenguaje y ejemplos muy simples. Es la mejor opción para un principiante y, además, no es muy grande. Entre lecturas más serias, tenemos libros de Robert Lafore y Robert Sedgewick. Ambos están escritos en Java, lo que te facilitará un poco el aprendizaje. ¡Después de todo, estás bastante familiarizado con este idioma! :) Para estudiantes con buenas habilidades matemáticas, la mejor opción es el libro de Thomas Cormen . ¡Pero la teoría por sí sola no te llenará la barriga! ¡Conocimiento! = Habilidad . Puede practicar la resolución de problemas que involucran algoritmos en HackerRank y LeetCode . Las tareas de estos sitios web a menudo se usan incluso durante las entrevistas en Google y Facebook, por lo que definitivamente no se aburrirá :) Para reforzar este material de lección, le recomiendo que vea este excelente video sobre la notación O grande en YouTube. ¡Nos vemos en las próximas lecciones! :)
Dicho esto, este tema es muy importante para todo programador. Vamos a hablar de algoritmos . ¿Qué es un algoritmo? En términos simples, es una secuencia de acciones que deben completarse para lograr un resultado deseado . Usamos algoritmos a menudo en la vida cotidiana. Por ejemplo, cada mañana tienes una tarea específica: ir a la escuela o al trabajo, y al mismo tiempo ser:
En este caso, el algoritmo más eficiente es enviar el archivo a través de Internet. ¡No podría tomar más de un par de minutos! Repitamos nuestro algoritmo: "Si desea transferir información en forma de archivos a una distancia de 5000 millas, debe enviar los datos a través de Internet". Excelente. Ahora vamos a analizarlo. ¿Cumple con nuestra tarea?Bueno, sí, lo hace. Pero, ¿qué podemos decir de su complejidad? Hmm, ahora las cosas se están poniendo más interesantes. El hecho es que nuestro algoritmo depende mucho de los datos de entrada, es decir, del tamaño de los archivos. Si tenemos 10 megas, entonces todo está bien. Pero, ¿y si necesitamos enviar 500 megas? 20 gigas? 500 terabytes? 30 petabytes? ¿Dejará de funcionar nuestro algoritmo? No, todas estas cantidades de datos sí se pueden transferir. ¿Tomará más tiempo? ¡Sí, lo hará! Ahora conocemos una característica importante de nuestro algoritmo: cuanto mayor sea la cantidad de datos a enviar, más tiempo llevará ejecutar el algoritmo.. Pero nos gustaría tener una comprensión más precisa de esta relación (entre el tamaño de los datos de entrada y el tiempo necesario para enviarlos). En nuestro caso, la complejidad algorítmica es lineal . "Lineal" significa que a medida que aumenta la cantidad de datos de entrada, el tiempo que se tarda en enviarlos aumentará de forma aproximadamente proporcional. Si la cantidad de datos se duplica, el tiempo necesario para enviarlos será el doble. Si los datos aumentan 10 veces, el tiempo de transmisión aumentará 10 veces. Usando la notación O grande, la complejidad de nuestro algoritmo se expresa como O(n). Debe recordar esta notación para el futuro: siempre se usa para algoritmos con complejidad lineal. Tenga en cuenta que no estamos hablando de varias cosas que pueden variar aquí: la velocidad de Internet, la potencia de cómputo de nuestra computadora, etc. Al evaluar la complejidad de un algoritmo, simplemente no tiene sentido considerar estos factores; en cualquier caso, están fuera de nuestro control. La notación Big O expresa la complejidad del algoritmo en sí, no el "entorno" en el que se ejecuta. Sigamos con nuestro ejemplo. Supongamos que finalmente nos enteramos de que necesitamos enviar archivos por un total de 800 terabytes. Por supuesto, podemos realizar nuestra tarea enviándolos a través de Internet. Solo hay un problema: a velocidades de transmisión de datos domésticas estándar (100 megabits por segundo), tardará aproximadamente 708 días. ¡Casi 2 años! :O Nuestro algoritmo obviamente no encaja bien aquí. ¡Necesitamos otra solución! ¡Inesperadamente, el gigante de TI Amazon viene a rescatarnos! El servicio Snowmobile de Amazon nos permite cargar una gran cantidad de datos en el almacenamiento móvil y luego enviarlos a la dirección deseada por camión. 
Entonces, ¡tenemos un nuevo algoritmo! "Si desea transferir información en forma de archivos a una distancia de 5000 millas y hacerlo tardaría más de 14 días en enviarse a través de Internet, debe enviar los datos en un camión de Amazon". Elegimos 14 días arbitrariamente aquí. Digamos que este es el período más largo que podemos esperar. Analicemos nuestro algoritmo. ¿Qué pasa con su velocidad? Incluso si el camión viaja a solo 50 mph, cubrirá 5000 millas en solo 100 horas. ¡Esto es un poco más de cuatro días! Esto es mucho mejor que la opción de enviar los datos a través de Internet. ¿Y qué hay de la complejidad de este algoritmo? ¿Es también lineal, es decir, O(n)? No, no es. Después de todo, al camión no le importa qué tan pesado lo cargues, seguirá conduciendo aproximadamente a la misma velocidad y llegará a tiempo. Ya sea que tengamos 800 terabytes o 10 veces más, el camión aún llegará a su destino en 5 días. En otras palabras, el algoritmo de transferencia de datos basado en camiones tiene una complejidad constante. Aquí, "constante" significa que no depende del tamaño de los datos de entrada. Coloque una unidad flash de 1GB en el camión, llegará dentro de los 5 días. Coloque discos que contengan 800 terabytes de datos, llegará dentro de los 5 días. Cuando se usa la notación O grande, la complejidad constante se denota por O(1) . Nos hemos familiarizado con O(n) y O(1) , así que ahora veamos más ejemplos en el mundo de la programación :) Suponga que tiene una matriz de 100 números y la tarea es mostrar cada uno de ellos en la consola. Escribes un 
En la fila superior de la imagen, vemos una matriz ordenada. Necesitamos encontrar el número 23 en él. En lugar de iterar sobre los números, simplemente dividimos la matriz en 2 partes y verificamos el número del medio en la matriz. Encuentra el número que se encuentra en la celda 4 y compruébalo (segunda fila en la imagen). Este número es 16 y estamos buscando 23. El número actual es menor que lo que estamos buscando. ¿Qué significa eso? Esto significa quetodos los números anteriores (aquellos ubicados antes del número 16) no necesitan ser verificados : ¡se garantiza que son menores que el que estamos buscando, porque nuestra matriz está ordenada! Continuamos la búsqueda entre los 5 elementos restantes. Nota:hemos realizado una sola comparación, pero ya hemos eliminado la mitad de las opciones posibles. Solo nos quedan 5 elementos. Repetiremos nuestro paso anterior dividiendo una vez más el subarreglo restante por la mitad y tomando nuevamente el elemento del medio (la tercera fila en la imagen). El número es 56 y es más grande que el que estamos buscando. ¿Qué significa eso? Significa que hemos eliminado otras 3 posibilidades: el propio número 56 y los dos números que le siguen (ya que se garantiza que son mayores que 23, porque la matriz está ordenada). Solo nos quedan 2 números para verificar (la última fila en la imagen): los números con índices de matriz 5 y 6. Verificamos el primero de ellos y encontramos lo que estábamos buscando: ¡el número 23! ¡Su índice es 5! Veamos los resultados de nuestro algoritmo y luego Analizaré su complejidad. Por cierto, ahora entiendes por qué esto se llama búsqueda binaria: se basa en dividir repetidamente los datos por la mitad. ¡El resultado es impresionante! Si usáramos una búsqueda lineal para buscar el número, necesitaríamos hasta 10 comparaciones, pero con una búsqueda binaria, ¡logramos la tarea con solo 3! En el peor de los casos, habría 4 comparaciones (si en el último paso el número que queríamos fuera la segunda de las posibilidades restantes, en lugar de la primera. Entonces, ¿qué hay de su complejidad? Este es un punto muy interesante :) El algoritmo de búsqueda binaria depende mucho menos del número de elementos en la matriz que el algoritmo de búsqueda lineal (es decir, iteración simple). Con 10 elementos en la matriz, una búsqueda lineal necesitará un máximo de 10 comparaciones, pero una búsqueda binaria necesitará un máximo de 4 comparaciones. Esa es una diferencia por un factor de 2.5. Pero para una matriz de 1000 elementos , una búsqueda lineal necesitará hasta 1000 comparaciones, ¡pero una búsqueda binaria solo requerirá 10 ! ¡La diferencia ahora es 100 veces mayor! Nota:el número de elementos en la matriz ha aumentado 100 veces (de 10 a 1000), pero el número de comparaciones requeridas para una búsqueda binaria ha aumentado por un factor de solo 2,5 (de 4 a 10). Si llegamos a 10.000 elementos , la diferencia será aún más impresionante: 10.000 comparaciones para búsqueda lineal, y un total de 14 comparaciones para búsqueda binaria. Y nuevamente, si la cantidad de elementos aumenta 1000 veces (de 10 a 10000), entonces la cantidad de comparaciones aumenta en un factor de solo 3.5 (de 4 a 14). La complejidad del algoritmo de búsqueda binaria es logarítmica o, si usamos la notación O grande, O(log n). ¿Por qué se llama así? El logaritmo es como el opuesto de la exponenciación. El logaritmo binario es la potencia a la que se debe elevar el número 2 para obtener un número. Por ejemplo, tenemos 10.000 elementos que necesitamos buscar usando el algoritmo de búsqueda binaria. 
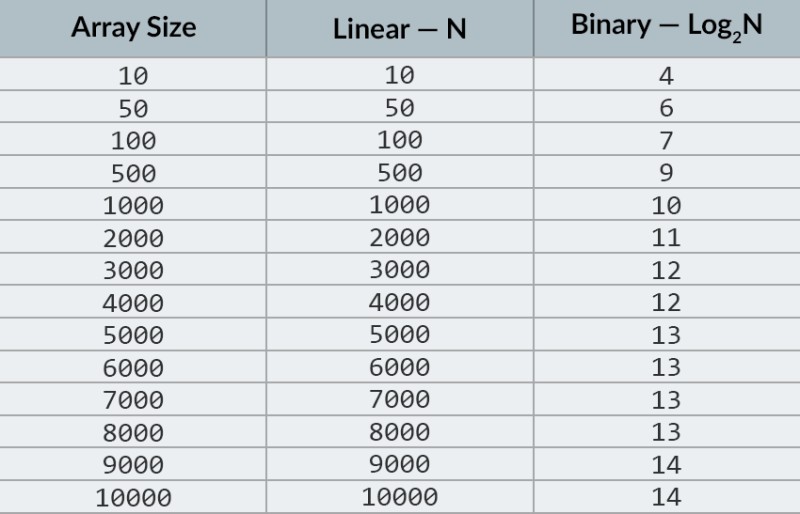Actualmente, puede mirar la tabla de valores para saber que hacer esto requerirá un máximo de 14 comparaciones. Pero, ¿qué sucede si nadie ha proporcionado una tabla de este tipo y necesita calcular el número máximo exacto de comparaciones? Solo necesita responder una pregunta simple: ¿ a qué potencia necesita elevar el número 2 para que el resultado sea mayor o igual que la cantidad de elementos a verificar? Por 10.000, es la potencia 14. 2 a la potencia 13 es demasiado pequeño (8192), pero 2 a la potencia 14 = 16384, y este número satisface nuestra condición (es mayor o igual que el número de elementos en la matriz). Encontramos el logaritmo: 14. ¡Esas son las comparaciones que podríamos necesitar! :) Los algoritmos y la complejidad algorítmica es un tema demasiado amplio para caber en una lección. Pero saberlo es muy importante: muchas entrevistas de trabajo involucrarán preguntas que involucran algoritmos. En teoría, puedo recomendarte algunos libros. Puede comenzar con " Algoritmos de Grokking ". Los ejemplos de este libro están escritos en Python, pero el libro utiliza un lenguaje y ejemplos muy simples. Es la mejor opción para un principiante y, además, no es muy grande. Entre lecturas más serias, tenemos libros de Robert Lafore y Robert Sedgewick. Ambos están escritos en Java, lo que te facilitará un poco el aprendizaje. ¡Después de todo, estás bastante familiarizado con este idioma! :) Para estudiantes con buenas habilidades matemáticas, la mejor opción es el libro de Thomas Cormen . ¡Pero la teoría por sí sola no te llenará la barriga! ¡Conocimiento! = Habilidad . Puede practicar la resolución de problemas que involucran algoritmos en HackerRank y LeetCode . Las tareas de estos sitios web a menudo se usan incluso durante las entrevistas en Google y Facebook, por lo que definitivamente no se aburrirá :) Para reforzar este material de lección, le recomiendo que vea este excelente video sobre la notación O grande en YouTube. ¡Nos vemos en las próximas lecciones! :)
GO TO FULL VERSION