Complexité algorithmique

Salut! La leçon d'aujourd'hui sera légèrement différente des autres. Il diffère en ce qu'il n'est qu'indirectement lié à Java. Cela dit, ce sujet est très important pour chaque programmeur. Nous allons parler d' algorithmes . Qu'est-ce qu'un algorithme ? En termes simples, il s'agit d'une séquence d'actions qui doivent être complétées pour obtenir un résultat souhaité . Nous utilisons souvent des algorithmes dans la vie de tous les jours. Par exemple, chaque matin vous avez une tâche précise : aller à l'école ou au travail, et en même temps être :

• Habillé
• Faire le ménage
• nourris

Quel algorithme vous permet d'atteindre ce résultat ?

1. Réveillez-vous à l'aide d'un réveil.
2. Prenez une douche et lavez-vous.
3. Préparez le petit-déjeuner et du café ou du thé.
4. Manger.
5. Si vous n'avez pas repassé vos vêtements la veille au soir, repassez-les.
6. S'habiller.
7. Quitter la maison.

Cette séquence d'actions vous permettra certainement d'obtenir le résultat souhaité. En programmation, nous travaillons constamment pour accomplir des tâches. Une partie importante de ces tâches peut être effectuée à l'aide d'algorithmes déjà connus. Par exemple, supposons que votre tâche consiste à : trier une liste de 100 noms dans un tableau . Cette tâche est assez simple, mais elle peut être résolue de différentes manières. Voici une solution possible : Algorithme de tri alphabétique des noms :

1. Achetez ou téléchargez l'édition 1961 du troisième nouveau dictionnaire international de Webster.
2. Trouvez tous les noms de notre liste dans ce dictionnaire.
3. Sur une feuille de papier, écrivez la page du dictionnaire sur laquelle se trouve le nom.
4. Utilisez les morceaux de papier pour trier les noms.

Une telle séquence d'actions accomplira-t-elle notre tâche ? Oui, ce sera certainement le cas. Cette solution est- elle efficace ? À peine. Nous arrivons ici à un autre aspect très important des algorithmes : leur efficacité . Il existe plusieurs façons d'accomplir cette tâche. Mais à la fois dans la programmation et dans la vie ordinaire, nous voulons choisir le moyen le plus efficace. Si votre tâche est de faire un toast beurré, vous pouvez commencer par semer du blé et traire une vache. Mais ce serait inefficacesolution — cela prendra beaucoup de temps et coûtera beaucoup d'argent. Vous pouvez accomplir votre tâche simple en achetant simplement du pain et du beurre. Bien qu'il vous permette de résoudre le problème, l'algorithme impliquant du blé et une vache est trop complexe pour être utilisé en pratique. En programmation, nous avons une notation spéciale appelée notation grand O pour évaluer la complexité des algorithmes. Big O permet d'évaluer à quel point le temps d'exécution d'un algorithme dépend de la taille des données d'entrée . Prenons l'exemple le plus simple : le transfert de données. Imaginez que vous ayez besoin d'envoyer des informations sous forme de fichier sur une longue distance (par exemple, 5000 miles). Quel algorithme serait le plus efficace ? Cela dépend des données avec lesquelles vous travaillez. Par exemple, supposons que nous ayons un fichier audio de 10 Mo. Dans ce cas, l'algorithme le plus efficace consiste à envoyer le fichier sur Internet. Cela ne pouvait pas prendre plus de quelques minutes ! Reprenons notre algorithme : "Si vous souhaitez transférer des informations sous forme de fichiers sur une distance de 5000 miles, vous devez envoyer les données via Internet". Excellent. Analysons-le maintenant. Accomplit-il notre tâche ?Eh bien, oui, c'est le cas. Mais que dire de sa complexité ? Hmm, maintenant les choses deviennent plus intéressantes. Le fait est que notre algorithme est très dépendant des données d'entrée, à savoir la taille des fichiers. Si nous avons 10 mégaoctets, alors tout va bien. Mais que se passe-t-il si nous devons envoyer 500 mégaoctets ? 20 gigaoctets ? 500 téraoctets ? 30 pétaoctets ? Notre algorithme cessera-t-il de fonctionner ? Non, toutes ces quantités de données peuvent effectivement être transférées. Cela prendra-t-il plus de temps ? Oui, il sera! Nous connaissons maintenant une caractéristique importante de notre algorithme : plus la quantité de données à envoyer est importante, plus il faudra de temps pour exécuter l'algorithme.. Mais nous aimerions avoir une compréhension plus précise de cette relation (entre la taille des données d'entrée et le temps nécessaire pour les envoyer). Dans notre cas, la complexité algorithmique est linéaire . "Linéaire" signifie qu'à mesure que la quantité de données d'entrée augmente, le temps nécessaire pour l'envoyer augmentera approximativement proportionnellement. Si la quantité de données double, le temps nécessaire pour l'envoyer sera deux fois plus long. Si les données augmentent de 10 fois, le temps de transmission augmentera de 10 fois. En utilisant la notation grand O, la complexité de notre algorithme est exprimée en O(n). Vous devriez vous souvenir de cette notation pour l'avenir — elle est toujours utilisée pour les algorithmes à complexité linéaire. Notez que nous ne parlons pas ici de plusieurs choses qui peuvent varier : la vitesse d'Internet, la puissance de calcul de notre ordinateur, etc. Lors de l'évaluation de la complexité d'un algorithme, il n'est tout simplement pas logique de prendre en compte ces facteurs - en tout état de cause, ils sont hors de notre contrôle. La notation Big O exprime la complexité de l'algorithme lui-même, pas "l'environnement" dans lequel il s'exécute. Continuons avec notre exemple. Supposons que nous apprenions finalement que nous devons envoyer des fichiers totalisant 800 téraoctets. Nous pouvons, bien sûr, accomplir notre tâche en les envoyant sur Internet. Il y a juste un problème : aux débits de transmission de données domestiques standard (100 mégabits par seconde), cela prendra environ 708 jours. Presque 2 ans! :O Notre algorithme n'est évidemment pas un bon ajustement ici. Il nous faut une autre solution ! De manière inattendue, le géant informatique Amazon vient à notre secours ! Le service Snowmobile d'Amazon nous permet de télécharger une grande quantité de données sur le stockage mobile, puis de les livrer à l'adresse souhaitée par camion ! Donc, nous avons un nouvel algorithme ! "Si vous souhaitez transférer des informations sous forme de fichiers sur une distance de 5000 miles et que cela prendrait plus de 14 jours à envoyer via Internet, vous devez envoyer les données sur un camion Amazon." Nous avons choisi 14 jours arbitrairement ici. Disons que c'est la période la plus longue que nous puissions attendre. Analysons notre algorithme. Qu'en est-il de sa vitesse ? Même si le camion ne roule qu'à 80 km/h, il parcourra 8 000 km en seulement 100 heures. C'est un peu plus de quatre jours ! C'est beaucoup mieux que l'option d'envoyer les données sur Internet. Et qu'en est-il de la complexité de cet algorithme ? Est-il aussi linéaire, c'est-à-dire O(n) ? Non, ce n'est pas le cas. Après tout, le camion ne se soucie pas de la charge que vous le chargez - il roulera toujours à peu près à la même vitesse et arrivera à l'heure. Que nous ayons 800 téraoctets, ou 10 fois plus, le camion atteindra toujours sa destination dans les 5 jours. En d'autres termes, l'algorithme de transfert de données basé sur les camions a une complexité constante. Ici, "constant" signifie qu'il ne dépend pas de la taille des données d'entrée. Mettez une clé USB de 1 Go dans le camion, elle arrivera dans les 5 jours. Mis dans des disques contenant 800 téraoctets de données, il arrivera dans les 5 jours. Lors de l'utilisation de la notation grand O, la complexité constante est notée O(1) . Nous nous sommes familiarisés avec O(n) et O(1) , alors regardons maintenant plus d'exemples dans le monde de la programmation :) Supposons qu'on vous donne un tableau de 100 nombres, et que la tâche consiste à afficher chacun d'eux sur la console. Vous écrivez une boucle ordinaire forqui effectue cette tâche

int[] numbers = new int[100];
// ...fill the array with numbers

for (int i: numbers) {
   System.out.println(i);
}

Quelle est la complexité de cet algorithme ? Linéaire, c'est-à-dire O(n). Le nombre d'actions que le programme doit effectuer dépend du nombre de numéros qui lui sont transmis. S'il y a 100 nombres dans le tableau, il y aura 100 actions (instructions pour afficher des chaînes à l'écran). S'il y a 10 000 nombres dans le tableau, alors 10 000 actions doivent être effectuées. Notre algorithme peut-il être amélioré de quelque manière que ce soit ? Non. Quoi qu'il en soit, nous devrons effectuer N passages dans le tableau et exécuter N instructions pour afficher les chaînes sur la console. Prenons un autre exemple.

public static void main(String[] args) {

   LinkedList<Integer> numbers = new LinkedList<>();
   numbers.add(0, 20202);
   numbers.add(0, 123);
   numbers.add(0, 8283);
}

Nous avons un vide LinkedListdans lequel nous insérons plusieurs nombres. Nous devons évaluer la complexité algorithmique de l'insertion d'un seul numéro dans le LinkedListdans notre exemple, et comment cela dépend du nombre d'éléments dans la liste. La réponse est O(1), c'est-à-dire une complexité constante . Pourquoi? Notez que nous insérons chaque numéro au début de la liste. De plus, vous vous souviendrez que lorsque vous insérez un nombre dans un LinkedList, les éléments ne se déplacent nulle part. Les liens (ou références) sont mis à jour (si vous avez oublié comment fonctionne LinkedList, regardez une de nos anciennes leçons ). Si le premier nombre de notre liste est x, et que nous insérons le nombre y au début de la liste, alors tout ce que nous devons faire est ceci :

x.previous  = y;
y.previous = null;
y.next = x;

Lorsque nous mettons à jour les liens, nous ne nous soucions pas du nombre de chiffres déjà présents dans leLinkedList , qu'il s'agisse d'un ou d'un milliard. La complexité de l'algorithme est constante, c'est-à-dire O(1).

Complexité logarithmique

Ne pas paniquer! :) Si le mot "logarithmique" vous donne envie de clore cette leçon et d'arrêter de lire, attendez quelques minutes. Il n'y aura pas de maths folles ici (il y a beaucoup d'explications comme ça ailleurs), et nous allons séparer chaque exemple. Imaginez que votre tâche consiste à trouver un nombre spécifique dans un tableau de 100 nombres. Plus précisément, vous devez vérifier s'il est là ou non. Dès que le nombre requis est trouvé, la recherche se termine, et vous affichez ceci dans la console : "Le nombre requis a été trouvé ! Son index dans le tableau = ...." Comment accompliriez-vous cette tâche ? Ici, la solution est évidente : vous devez parcourir les éléments du tableau un par un, en commençant par le premier (ou par le dernier) et vérifier si le nombre actuel correspond à celui que vous recherchez. Par conséquent, le nombre d'actions dépend directement du nombre d'éléments dans le tableau. Si nous avons 100 nombres, nous pourrions avoir besoin d'aller à l'élément suivant 100 fois et d'effectuer 100 comparaisons. S'il y a 1000 nombres, alors il pourrait y avoir 1000 comparaisons. Il s'agit évidemment de complexité linéaire, c'est-à-direO(n) . Et maintenant, nous allons ajouter un raffinement à notre exemple : le tableau dans lequel vous devez trouver le nombre est trié par ordre croissant . Cela change-t-il quelque chose par rapport à notre tâche ? Nous pourrions toujours effectuer une recherche par force brute pour le nombre souhaité. Mais alternativement, nous pourrions utiliser l' algorithme de recherche binaire bien connu .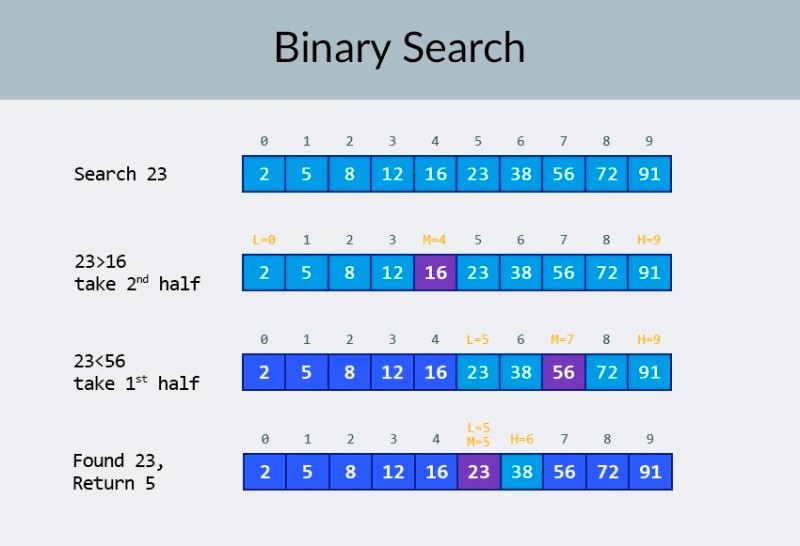 Dans la rangée supérieure de l'image, nous voyons un tableau trié. Nous devons trouver le nombre 23 dedans. Au lieu d'itérer sur les nombres, nous divisons simplement le tableau en 2 parties et vérifions le nombre du milieu dans le tableau. Trouvez le numéro qui se trouve dans la cellule 4 et vérifiez-le (deuxième ligne de l'image). Ce nombre est 16 et nous en recherchons 23. Le nombre actuel est inférieur à ce que nous recherchons. Qu'est-ce que cela signifie? Cela signifie quetous les nombres précédents (ceux situés avant le nombre 16) n'ont pas besoin d'être vérifiés : ils sont garantis inférieurs à celui que nous recherchons, car notre tableau est trié ! On continue la recherche parmi les 5 éléments restants. Note:nous n'avons effectué qu'une seule comparaison, mais nous avons déjà éliminé la moitié des options possibles. Il ne nous reste que 5 éléments. Nous allons répéter notre étape précédente en divisant à nouveau le sous-tableau restant en deux et en prenant à nouveau l'élément du milieu (la 3ème rangée de l'image). Le nombre est 56, et il est plus grand que celui que nous recherchons. Qu'est-ce que cela signifie? Cela signifie que nous avons éliminé 3 autres possibilités : le nombre 56 lui-même ainsi que les deux nombres qui le suivent (puisqu'ils sont garantis supérieurs à 23, car le tableau est trié). Il ne nous reste plus que 2 nombres à vérifier (la dernière ligne de l'image) - les nombres avec les indices de tableau 5 et 6. Nous vérifions le premier d'entre eux et trouvons ce que nous cherchions - le nombre 23 ! Son indice est 5 ! Regardons les résultats de notre algorithme, puis nous ' Je vais analyser sa complexité. Au fait, vous comprenez maintenant pourquoi cela s'appelle la recherche binaire : elle repose sur la division répétée des données en deux. Le résultat est impressionnant ! Si nous utilisions une recherche linéaire pour rechercher le nombre, nous aurions besoin de jusqu'à 10 comparaisons, mais avec une recherche binaire, nous avons accompli la tâche avec seulement 3 ! Dans le pire des cas, il y aurait 4 comparaisons (si à la dernière étape le nombre que l'on voulait était la deuxième des possibilités restantes, plutôt que la première. Alors qu'en est-il de sa complexité ? C'est un point très intéressant :) L'algorithme de recherche binaire dépend beaucoup moins du nombre d'éléments dans le tableau que l'algorithme de recherche linéaire (c'est-à-dire une simple itération). Avec 10 éléments dans le tableau, une recherche linéaire nécessitera un maximum de 10 comparaisons, mais une recherche binaire nécessitera un maximum de 4 comparaisons. C'est une différence d'un facteur 2,5. Mais pour un tableau de 1000 éléments , une recherche linéaire nécessitera jusqu'à 1000 comparaisons, alors qu'une recherche binaire n'en nécessiterait que 10 ! La différence est maintenant 100 fois supérieure ! Note:le nombre d'éléments dans le tableau a augmenté de 100 fois (de 10 à 1000), mais le nombre de comparaisons requises pour une recherche binaire a augmenté d'un facteur de seulement 2,5 (de 4 à 10). Si nous arrivons à 10 000 éléments , la différence sera encore plus impressionnante : 10 000 comparaisons pour la recherche linéaire, et un total de 14 comparaisons pour la recherche binaire. Et encore une fois, si le nombre d'éléments augmente de 1000 fois (de 10 à 10000), alors le nombre de comparaisons augmente d'un facteur de seulement 3,5 (de 4 à 14). La complexité de l'algorithme de recherche binaire est logarithmique , ou, si nous utilisons la notation grand O, O(log n). pourquoi c'est appelé comme ça? Le logarithme est comme le contraire de l'exponentiation. Le logarithme binaire est la puissance à laquelle il faut élever le nombre 2 pour obtenir un nombre. Par exemple, nous avons 10 000 éléments que nous devons rechercher à l'aide de l'algorithme de recherche binaire. 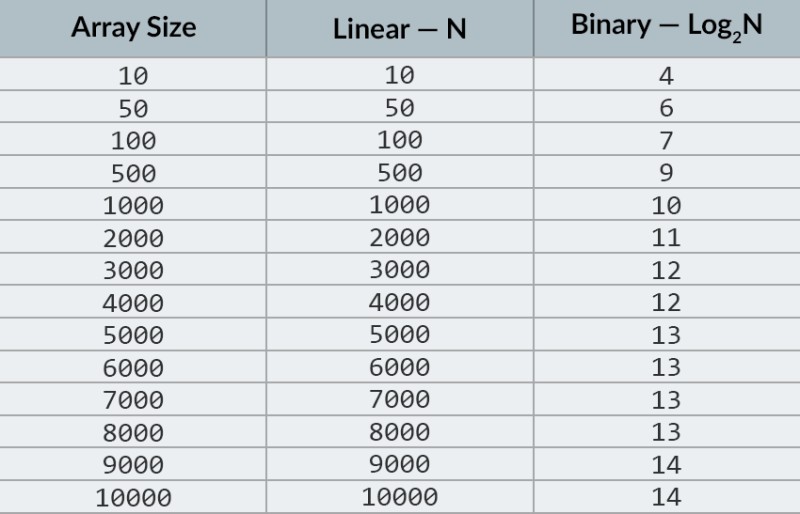Actuellement, vous pouvez consulter le tableau des valeurs pour savoir que cela nécessitera un maximum de 14 comparaisons. Mais que se passe-t-il si personne n'a fourni un tel tableau et que vous devez calculer le nombre maximum exact de comparaisons ? Il vous suffit de répondre à une question simple : à quelle puissance faut-il élever le nombre 2 pour que le résultat soit supérieur ou égal au nombre d'éléments à vérifier ? Pour 10 000, c'est la puissance 14. 2 à la puissance 13 est trop petit (8192), mais 2 à la puissance 14 = 16384, et ce nombre satisfait notre condition (il est supérieur ou égal au nombre d'éléments du tableau). Nous avons trouvé le logarithme : 14. C'est le nombre de comparaisons dont nous pourrions avoir besoin ! :) Les algorithmes et la complexité algorithmique sont un sujet trop vaste pour tenir dans une seule leçon. Mais le savoir est très important : de nombreux entretiens d'embauche impliqueront des questions impliquant des algorithmes. Pour la théorie, je peux vous recommander quelques livres. Vous pouvez commencer par " Grokking Algorithms ". Les exemples de ce livre sont écrits en Python, mais le livre utilise un langage et des exemples très simples. C'est la meilleure option pour un débutant et, en plus, ce n'est pas très grand. Parmi les lectures plus sérieuses, nous avons des livres de Robert Lafore et Robert Sedgewick. Les deux sont écrits en Java, ce qui vous facilitera un peu l'apprentissage. Après tout, vous connaissez bien cette langue ! :) Pour les étudiants ayant de bonnes compétences en mathématiques, la meilleure option est le livre de Thomas Cormen . Mais la théorie seule ne remplira pas votre ventre ! Connaissance != Capacité . Vous pouvez vous entraîner à résoudre des problèmes impliquant des algorithmes sur HackerRank et LeetCode . Les tâches de ces sites Web sont souvent utilisées même lors d'entretiens chez Google et Facebook, vous ne vous ennuierez donc certainement pas :) Pour renforcer ce matériel de cours, je vous recommande de regarder cette excellente vidéo sur la notation Big O sur YouTube. A bientôt dans les prochains cours ! :)