CIAO! La lezione di oggi sarà leggermente diversa dalle altre. Differirà in quanto è solo indirettamente correlato a Java. ![Complessità algoritmica - 1]()
Detto questo, questo argomento è molto importante per ogni programmatore. Parleremo di algoritmi . Cos'è un algoritmo? In termini semplici, è una sequenza di azioni che devono essere completate per ottenere un risultato desiderato . Utilizziamo algoritmi spesso nella vita di tutti i giorni. Ad esempio, ogni mattina hai un compito specifico: andare a scuola o al lavoro, e allo stesso tempo essere:
![Complessità algoritmica - 2]()
In questo caso, l'algoritmo più efficiente consiste nell'inviare il file tramite Internet. Non potevano volerci più di un paio di minuti! Riformuliamo il nostro algoritmo: "Se desideri trasferire informazioni sotto forma di file su una distanza di 5000 miglia, devi inviare i dati tramite Internet". Eccellente. Ora analizziamolo. Assolve il nostro compito?Beh, sì, lo fa. Ma cosa possiamo dire della sua complessità? Hmm, ora le cose si fanno più interessanti. Il fatto è che il nostro algoritmo dipende molto dai dati di input, ovvero dalla dimensione dei file. Se abbiamo 10 megabyte, allora va tutto bene. Ma cosa succede se dobbiamo inviare 500 megabyte? 20 gigabyte? 500 terabyte? 30 petabyte? Il nostro algoritmo smetterà di funzionare? No, tutte queste quantità di dati possono effettivamente essere trasferite. Ci vorrà più tempo? Si lo farà! Ora conosciamo un'importante caratteristica del nostro algoritmo: maggiore è la quantità di dati da inviare, maggiore sarà il tempo necessario per eseguire l'algoritmo. Ma vorremmo avere una comprensione più precisa di questa relazione (tra la dimensione dei dati di input e il tempo necessario per inviarli). Nel nostro caso, la complessità algoritmica è lineare . "Lineare" significa che all'aumentare della quantità di dati di input, il tempo necessario per inviarli aumenterà in modo approssimativamente proporzionale. Se la quantità di dati raddoppia, il tempo necessario per inviarli sarà il doppio. Se i dati aumentano di 10 volte, il tempo di trasmissione aumenterà di 10 volte. Usando la notazione O grande, la complessità del nostro algoritmo è espressa come O(n). Dovresti ricordare questa notazione per il futuro: è sempre usata per algoritmi con complessità lineare. Nota che non stiamo parlando di diverse cose che possono variare qui: velocità di Internet, potenza di calcolo del nostro computer e così via. Quando si valuta la complessità di un algoritmo, semplicemente non ha senso considerare questi fattori, in ogni caso sono al di fuori del nostro controllo. La notazione Big O esprime la complessità dell'algoritmo stesso, non l'"ambiente" in cui viene eseguito. Continuiamo con il nostro esempio. Supponiamo che alla fine apprendiamo che dobbiamo inviare file per un totale di 800 terabyte. Possiamo, ovviamente, portare a termine il nostro compito inviandoli via Internet. C'è solo un problema: alla velocità di trasmissione dati domestica standard (100 megabit al secondo), ci vorranno circa 708 giorni. Quasi 2 anni! :O Il nostro algoritmo ovviamente non è adatto a questo caso. Abbiamo bisogno di qualche altra soluzione! Inaspettatamente, il gigante IT Amazon viene in nostro soccorso! Il servizio Snowmobile di Amazon ci consente di caricare una grande quantità di dati nell'archivio mobile e quindi di consegnarli all'indirizzo desiderato tramite camion! ![Complessità algoritmica - 3]()
Quindi, abbiamo un nuovo algoritmo! "Se desideri trasferire informazioni sotto forma di file su una distanza di 5000 miglia e per farlo ci vorrebbero più di 14 giorni per l'invio via Internet, dovresti inviare i dati su un camion Amazon." Abbiamo scelto arbitrariamente 14 giorni qui. Diciamo che questo è il periodo più lungo che possiamo aspettare. Analizziamo il nostro algoritmo. E la sua velocità? Anche se il camion viaggia a soli 50 mph, coprirà 5000 miglia in sole 100 ore. Sono poco più di quattro giorni! Questo è molto meglio dell'opzione di inviare i dati su Internet. E per quanto riguarda la complessità di questo algoritmo? È anche lineare, cioè O(n)? No non lo è. Dopotutto, al camion non importa quanto pesantemente lo carichi: continuerà a guidare all'incirca alla stessa velocità e arriverà in tempo. Sia che abbiamo 800 terabyte, o 10 volte tanto, il camion raggiungerà comunque la sua destinazione entro 5 giorni. In altre parole, l'algoritmo di trasferimento dei dati basato su camion ha una complessità costante. Qui, "costante" significa che non dipende dalla dimensione dei dati di input. Metti una chiavetta da 1 GB nel camion, arriverà entro 5 giorni. Inserito in dischi contenenti 800 terabyte di dati, arriverà entro 5 giorni. Quando si utilizza la notazione O grande, la complessità costante è indicata da O(1) . Abbiamo acquisito familiarità con O(n) e O(1) , quindi ora diamo un'occhiata ad altri esempi nel mondo della programmazione :) Supponiamo che ti venga dato un array di 100 numeri e che il compito sia quello di visualizzare ciascuno di essi su la consolle. Scrivi un ![Complessità algoritmica - 5]()
Nella riga superiore dell'immagine, vediamo un array ordinato. Dobbiamo trovare il numero 23 in esso. Invece di iterare sui numeri, dividiamo semplicemente l'array in 2 parti e controlliamo il numero centrale nell'array. Trova il numero che si trova nella cella 4 e controllalo (seconda riga nell'immagine). Questo numero è 16 e stiamo cercando 23. Il numero attuale è inferiore a quello che stiamo cercando. Che cosa significa? Significa chetutti i numeri precedenti (quelli che precedono il numero 16) non hanno bisogno di essere controllati : sono sicuramente inferiori a quello che stiamo cercando, perché il nostro array è ordinato! Continuiamo la ricerca tra i restanti 5 elementi. Nota:abbiamo effettuato un solo confronto, ma abbiamo già eliminato la metà delle possibili opzioni. Abbiamo solo 5 elementi rimasti. Ripeteremo il nostro passaggio precedente dividendo ancora una volta il sottoarray rimanente a metà e prendendo di nuovo l'elemento centrale (la terza riga nell'immagine). Il numero è 56 ed è più grande di quello che stiamo cercando. Che cosa significa? Significa che abbiamo eliminato altre 3 possibilità: il numero 56 stesso così come i due numeri successivi (poiché è garantito che siano maggiori di 23, perché l'array è ordinato). Abbiamo solo 2 numeri da controllare (l'ultima riga nell'immagine) — i numeri con gli indici di matrice 5 e 6. Controlliamo il primo di essi e troviamo quello che stavamo cercando — il numero 23! Il suo indice è 5! Diamo un'occhiata ai risultati del nostro algoritmo, e poi noi' Ne analizzerò la complessità. A proposito, ora capisci perché questa si chiama ricerca binaria: si basa sulla divisione ripetuta dei dati a metà. Il risultato è impressionante! Se usassimo una ricerca lineare per cercare il numero, avremmo bisogno di fino a 10 confronti, ma con una ricerca binaria, abbiamo portato a termine il compito con solo 3! Nel peggiore dei casi, ci sarebbero 4 confronti (se nell'ultimo passaggio il numero che volevamo fosse il secondo delle possibilità rimanenti, piuttosto che il primo. E la sua complessità? Questo è un punto molto interessante :) L'algoritmo di ricerca binaria è molto meno dipendente dal numero di elementi nell'array rispetto all'algoritmo di ricerca lineare (ovvero semplice iterazione). Con 10 elementi nell'array, una ricerca lineare avrà bisogno di un massimo di 10 confronti, ma una ricerca binaria avrà bisogno di un massimo di 4 confronti. Questa è una differenza di un fattore 2,5. Ma per un array di 1000 elementi , una ricerca lineare richiederà fino a 1000 confronti, ma una ricerca binaria ne richiederebbe solo 10 ! La differenza ora è di 100 volte! Nota:il numero di elementi nell'array è aumentato di 100 volte (da 10 a 1000), ma il numero di confronti richiesti per una ricerca binaria è aumentato solo di un fattore 2,5 (da 4 a 10). Se arriviamo a 10.000 elementi , la differenza sarà ancora più impressionante: 10.000 confronti per la ricerca lineare e un totale di 14 confronti per la ricerca binaria. E ancora, se il numero di elementi aumenta di 1000 volte (da 10 a 10000), allora il numero di confronti aumenta solo di un fattore 3,5 (da 4 a 14). La complessità dell'algoritmo di ricerca binaria è logaritmica o, se usiamo la notazione O grande, O(log n). Perché si chiama così? Il logaritmo è come l'opposto dell'elevamento a potenza. Il logaritmo binario è la potenza alla quale il numero 2 deve essere elevato per ottenere un numero. Ad esempio, abbiamo 10.000 elementi che dobbiamo cercare utilizzando l'algoritmo di ricerca binaria. ![Complessità algoritmica - 6]()
Attualmente, puoi guardare la tabella dei valori per sapere che per fare ciò saranno necessari un massimo di 14 confronti. Ma cosa succede se nessuno ha fornito una tabella del genere e devi calcolare il numero massimo esatto di confronti? Devi solo rispondere a una semplice domanda: a quale potenza devi elevare il numero 2 in modo che il risultato sia maggiore o uguale al numero di elementi da controllare? Per 10.000, è la quattordicesima potenza. 2 alla 13a potenza è troppo piccolo (8192), ma 2 alla 14a potenza = 16384, e questo numero soddisfa la nostra condizione (è maggiore o uguale al numero di elementi nell'array). Abbiamo trovato il logaritmo: 14. Ecco quanti confronti potremmo aver bisogno! :) Gli algoritmi e la complessità algoritmica sono un argomento troppo ampio per rientrare in una lezione. Ma saperlo è molto importante: molti colloqui di lavoro comporteranno domande che coinvolgono algoritmi. Per la teoria, posso consigliarti alcuni libri. Puoi iniziare con " Grokking Algorithms ". Gli esempi in questo libro sono scritti in Python, ma il libro utilizza un linguaggio ed esempi molto semplici. È l'opzione migliore per un principiante e, inoltre, non è molto grande. Tra le letture più serie, abbiamo i libri di Robert Lafore e Robert Sedgewick. Entrambi sono scritti in Java, il che renderà l'apprendimento un po' più facile per te. Dopotutto, conosci abbastanza bene questa lingua! :) Per gli studenti con buone capacità matematiche, l'opzione migliore è il libro di Thomas Cormen . Ma la teoria da sola non ti riempirà la pancia! Conoscenza != Capacità . Puoi esercitarti a risolvere problemi che coinvolgono algoritmi su HackerRank e LeetCode . Le attività di questi siti Web vengono spesso utilizzate anche durante le interviste su Google e Facebook, quindi sicuramente non ti annoierai :) Per rafforzare questo materiale didattico, ti consiglio di guardare questo eccellente video sulla notazione O grande su YouTube. Ci vediamo alle prossime lezioni! :)
Detto questo, questo argomento è molto importante per ogni programmatore. Parleremo di algoritmi . Cos'è un algoritmo? In termini semplici, è una sequenza di azioni che devono essere completate per ottenere un risultato desiderato . Utilizziamo algoritmi spesso nella vita di tutti i giorni. Ad esempio, ogni mattina hai un compito specifico: andare a scuola o al lavoro, e allo stesso tempo essere:
- Vestito
- Pulito
- Alimentato
- Svegliati usando una sveglia.
- Fatti una doccia e lavati.
- Prepara la colazione e un caffè o un tè.
- Mangiare.
- Se non hai stirato i vestiti la sera prima, stirali.
- Vestirsi.
- Uscire di casa.
- Acquista o scarica l'edizione 1961 del Webster's Third New International Dictionary.
- Trova tutti i nomi dalla nostra lista in questo dizionario.
- Su un pezzo di carta, scrivi la pagina del dizionario su cui si trova il nome.
- Usa i pezzi di carta per ordinare i nomi.
In questo caso, l'algoritmo più efficiente consiste nell'inviare il file tramite Internet. Non potevano volerci più di un paio di minuti! Riformuliamo il nostro algoritmo: "Se desideri trasferire informazioni sotto forma di file su una distanza di 5000 miglia, devi inviare i dati tramite Internet". Eccellente. Ora analizziamolo. Assolve il nostro compito?Beh, sì, lo fa. Ma cosa possiamo dire della sua complessità? Hmm, ora le cose si fanno più interessanti. Il fatto è che il nostro algoritmo dipende molto dai dati di input, ovvero dalla dimensione dei file. Se abbiamo 10 megabyte, allora va tutto bene. Ma cosa succede se dobbiamo inviare 500 megabyte? 20 gigabyte? 500 terabyte? 30 petabyte? Il nostro algoritmo smetterà di funzionare? No, tutte queste quantità di dati possono effettivamente essere trasferite. Ci vorrà più tempo? Si lo farà! Ora conosciamo un'importante caratteristica del nostro algoritmo: maggiore è la quantità di dati da inviare, maggiore sarà il tempo necessario per eseguire l'algoritmo. Ma vorremmo avere una comprensione più precisa di questa relazione (tra la dimensione dei dati di input e il tempo necessario per inviarli). Nel nostro caso, la complessità algoritmica è lineare . "Lineare" significa che all'aumentare della quantità di dati di input, il tempo necessario per inviarli aumenterà in modo approssimativamente proporzionale. Se la quantità di dati raddoppia, il tempo necessario per inviarli sarà il doppio. Se i dati aumentano di 10 volte, il tempo di trasmissione aumenterà di 10 volte. Usando la notazione O grande, la complessità del nostro algoritmo è espressa come O(n). Dovresti ricordare questa notazione per il futuro: è sempre usata per algoritmi con complessità lineare. Nota che non stiamo parlando di diverse cose che possono variare qui: velocità di Internet, potenza di calcolo del nostro computer e così via. Quando si valuta la complessità di un algoritmo, semplicemente non ha senso considerare questi fattori, in ogni caso sono al di fuori del nostro controllo. La notazione Big O esprime la complessità dell'algoritmo stesso, non l'"ambiente" in cui viene eseguito. Continuiamo con il nostro esempio. Supponiamo che alla fine apprendiamo che dobbiamo inviare file per un totale di 800 terabyte. Possiamo, ovviamente, portare a termine il nostro compito inviandoli via Internet. C'è solo un problema: alla velocità di trasmissione dati domestica standard (100 megabit al secondo), ci vorranno circa 708 giorni. Quasi 2 anni! :O Il nostro algoritmo ovviamente non è adatto a questo caso. Abbiamo bisogno di qualche altra soluzione! Inaspettatamente, il gigante IT Amazon viene in nostro soccorso! Il servizio Snowmobile di Amazon ci consente di caricare una grande quantità di dati nell'archivio mobile e quindi di consegnarli all'indirizzo desiderato tramite camion! 
Quindi, abbiamo un nuovo algoritmo! "Se desideri trasferire informazioni sotto forma di file su una distanza di 5000 miglia e per farlo ci vorrebbero più di 14 giorni per l'invio via Internet, dovresti inviare i dati su un camion Amazon." Abbiamo scelto arbitrariamente 14 giorni qui. Diciamo che questo è il periodo più lungo che possiamo aspettare. Analizziamo il nostro algoritmo. E la sua velocità? Anche se il camion viaggia a soli 50 mph, coprirà 5000 miglia in sole 100 ore. Sono poco più di quattro giorni! Questo è molto meglio dell'opzione di inviare i dati su Internet. E per quanto riguarda la complessità di questo algoritmo? È anche lineare, cioè O(n)? No non lo è. Dopotutto, al camion non importa quanto pesantemente lo carichi: continuerà a guidare all'incirca alla stessa velocità e arriverà in tempo. Sia che abbiamo 800 terabyte, o 10 volte tanto, il camion raggiungerà comunque la sua destinazione entro 5 giorni. In altre parole, l'algoritmo di trasferimento dei dati basato su camion ha una complessità costante. Qui, "costante" significa che non dipende dalla dimensione dei dati di input. Metti una chiavetta da 1 GB nel camion, arriverà entro 5 giorni. Inserito in dischi contenenti 800 terabyte di dati, arriverà entro 5 giorni. Quando si utilizza la notazione O grande, la complessità costante è indicata da O(1) . Abbiamo acquisito familiarità con O(n) e O(1) , quindi ora diamo un'occhiata ad altri esempi nel mondo della programmazione :) Supponiamo che ti venga dato un array di 100 numeri e che il compito sia quello di visualizzare ciascuno di essi su la consolle. Scrivi un forciclo ordinario che esegue questa attività
int[] numbers = new int[100];
// ...fill the array with numbers
for (int i: numbers) {
System.out.println(i);
}
public static void main(String[] args) {
LinkedList<Integer> numbers = new LinkedList<>();
numbers.add(0, 20202);
numbers.add(0, 123);
numbers.add(0, 8283);
}
LinkedListin cui inseriamo diversi numeri. Dobbiamo valutare la complessità algoritmica dell'inserimento di un singolo numero nel LinkedListnostro esempio e come dipende dal numero di elementi nell'elenco. La risposta è O(1), cioè complessità costante . Perché? Si noti che inseriamo ogni numero all'inizio dell'elenco. Inoltre, ricorderai che quando inserisci un numero in a LinkedList, gli elementi non si spostano da nessuna parte. I link (o riferimenti) sono aggiornati (se hai dimenticato come funziona LinkedList, guarda una delle nostre vecchie lezioni ). Se il primo numero nella nostra lista è x, e inseriamo il numero y all'inizio della lista, tutto quello che dobbiamo fare è questo:
x.previous = y;
y.previous = null;
y.next = x;
LinkedList , se uno o un miliardo. La complessità dell'algoritmo è costante, cioè O(1).
Complessità logaritmica
Niente panico! :) Se la parola "logaritmico" ti fa venire voglia di chiudere questa lezione e smettere di leggere, aspetta solo un paio di minuti. Non ci sarà alcuna matematica folle qui (ci sono molte spiegazioni del genere altrove) e selezioniamo ogni esempio. Immagina che il tuo compito sia trovare un numero specifico in una matrice di 100 numeri. Più precisamente, è necessario verificare se è presente o meno. Non appena viene trovato il numero richiesto, la ricerca termina e nella console viene visualizzato quanto segue: "Il numero richiesto è stato trovato! Il suo indice nell'array = ...." Come eseguiresti questa operazione? Qui la soluzione è ovvia: occorre iterare sugli elementi dell'array uno per uno, partendo dal primo (o dall'ultimo) e verificare se il numero corrente corrisponde a quello che si sta cercando. Di conseguenza, il numero di azioni dipende direttamente dal numero di elementi nell'array. Se abbiamo 100 numeri, potremmo potenzialmente dover passare all'elemento successivo 100 volte ed eseguire 100 confronti. Se ci sono 1000 numeri, potrebbero esserci 1000 confronti. Questa è ovviamente complessità lineare, vale a direO(n) . E ora aggiungeremo un perfezionamento al nostro esempio: l'array in cui è necessario trovare il numero è ordinato in ordine crescente . Questo cambia qualcosa rispetto al nostro compito? Potremmo ancora eseguire una ricerca a forza bruta per il numero desiderato. Ma in alternativa, potremmo usare il noto algoritmo di ricerca binaria .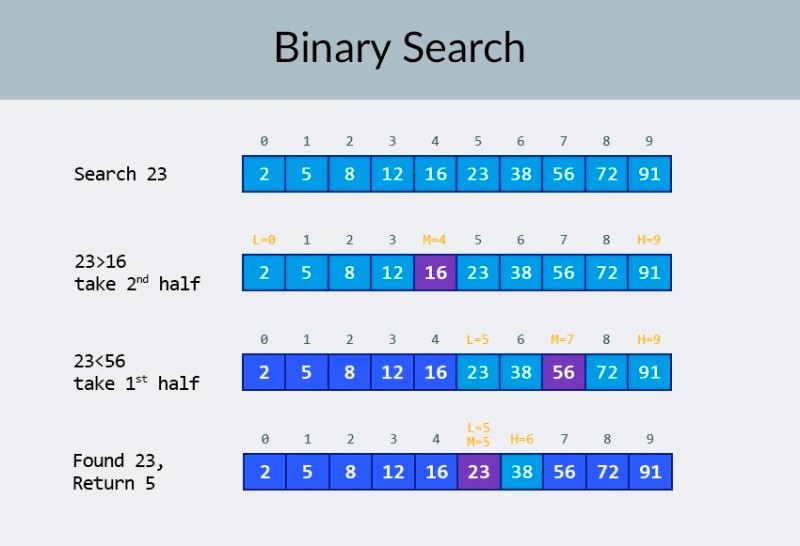
Nella riga superiore dell'immagine, vediamo un array ordinato. Dobbiamo trovare il numero 23 in esso. Invece di iterare sui numeri, dividiamo semplicemente l'array in 2 parti e controlliamo il numero centrale nell'array. Trova il numero che si trova nella cella 4 e controllalo (seconda riga nell'immagine). Questo numero è 16 e stiamo cercando 23. Il numero attuale è inferiore a quello che stiamo cercando. Che cosa significa? Significa chetutti i numeri precedenti (quelli che precedono il numero 16) non hanno bisogno di essere controllati : sono sicuramente inferiori a quello che stiamo cercando, perché il nostro array è ordinato! Continuiamo la ricerca tra i restanti 5 elementi. Nota:abbiamo effettuato un solo confronto, ma abbiamo già eliminato la metà delle possibili opzioni. Abbiamo solo 5 elementi rimasti. Ripeteremo il nostro passaggio precedente dividendo ancora una volta il sottoarray rimanente a metà e prendendo di nuovo l'elemento centrale (la terza riga nell'immagine). Il numero è 56 ed è più grande di quello che stiamo cercando. Che cosa significa? Significa che abbiamo eliminato altre 3 possibilità: il numero 56 stesso così come i due numeri successivi (poiché è garantito che siano maggiori di 23, perché l'array è ordinato). Abbiamo solo 2 numeri da controllare (l'ultima riga nell'immagine) — i numeri con gli indici di matrice 5 e 6. Controlliamo il primo di essi e troviamo quello che stavamo cercando — il numero 23! Il suo indice è 5! Diamo un'occhiata ai risultati del nostro algoritmo, e poi noi' Ne analizzerò la complessità. A proposito, ora capisci perché questa si chiama ricerca binaria: si basa sulla divisione ripetuta dei dati a metà. Il risultato è impressionante! Se usassimo una ricerca lineare per cercare il numero, avremmo bisogno di fino a 10 confronti, ma con una ricerca binaria, abbiamo portato a termine il compito con solo 3! Nel peggiore dei casi, ci sarebbero 4 confronti (se nell'ultimo passaggio il numero che volevamo fosse il secondo delle possibilità rimanenti, piuttosto che il primo. E la sua complessità? Questo è un punto molto interessante :) L'algoritmo di ricerca binaria è molto meno dipendente dal numero di elementi nell'array rispetto all'algoritmo di ricerca lineare (ovvero semplice iterazione). Con 10 elementi nell'array, una ricerca lineare avrà bisogno di un massimo di 10 confronti, ma una ricerca binaria avrà bisogno di un massimo di 4 confronti. Questa è una differenza di un fattore 2,5. Ma per un array di 1000 elementi , una ricerca lineare richiederà fino a 1000 confronti, ma una ricerca binaria ne richiederebbe solo 10 ! La differenza ora è di 100 volte! Nota:il numero di elementi nell'array è aumentato di 100 volte (da 10 a 1000), ma il numero di confronti richiesti per una ricerca binaria è aumentato solo di un fattore 2,5 (da 4 a 10). Se arriviamo a 10.000 elementi , la differenza sarà ancora più impressionante: 10.000 confronti per la ricerca lineare e un totale di 14 confronti per la ricerca binaria. E ancora, se il numero di elementi aumenta di 1000 volte (da 10 a 10000), allora il numero di confronti aumenta solo di un fattore 3,5 (da 4 a 14). La complessità dell'algoritmo di ricerca binaria è logaritmica o, se usiamo la notazione O grande, O(log n). Perché si chiama così? Il logaritmo è come l'opposto dell'elevamento a potenza. Il logaritmo binario è la potenza alla quale il numero 2 deve essere elevato per ottenere un numero. Ad esempio, abbiamo 10.000 elementi che dobbiamo cercare utilizzando l'algoritmo di ricerca binaria. 
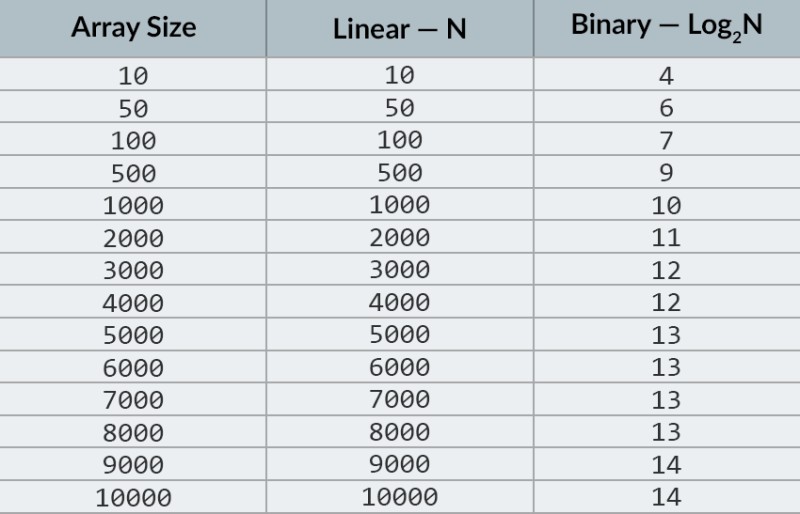Attualmente, puoi guardare la tabella dei valori per sapere che per fare ciò saranno necessari un massimo di 14 confronti. Ma cosa succede se nessuno ha fornito una tabella del genere e devi calcolare il numero massimo esatto di confronti? Devi solo rispondere a una semplice domanda: a quale potenza devi elevare il numero 2 in modo che il risultato sia maggiore o uguale al numero di elementi da controllare? Per 10.000, è la quattordicesima potenza. 2 alla 13a potenza è troppo piccolo (8192), ma 2 alla 14a potenza = 16384, e questo numero soddisfa la nostra condizione (è maggiore o uguale al numero di elementi nell'array). Abbiamo trovato il logaritmo: 14. Ecco quanti confronti potremmo aver bisogno! :) Gli algoritmi e la complessità algoritmica sono un argomento troppo ampio per rientrare in una lezione. Ma saperlo è molto importante: molti colloqui di lavoro comporteranno domande che coinvolgono algoritmi. Per la teoria, posso consigliarti alcuni libri. Puoi iniziare con " Grokking Algorithms ". Gli esempi in questo libro sono scritti in Python, ma il libro utilizza un linguaggio ed esempi molto semplici. È l'opzione migliore per un principiante e, inoltre, non è molto grande. Tra le letture più serie, abbiamo i libri di Robert Lafore e Robert Sedgewick. Entrambi sono scritti in Java, il che renderà l'apprendimento un po' più facile per te. Dopotutto, conosci abbastanza bene questa lingua! :) Per gli studenti con buone capacità matematiche, l'opzione migliore è il libro di Thomas Cormen . Ma la teoria da sola non ti riempirà la pancia! Conoscenza != Capacità . Puoi esercitarti a risolvere problemi che coinvolgono algoritmi su HackerRank e LeetCode . Le attività di questi siti Web vengono spesso utilizzate anche durante le interviste su Google e Facebook, quindi sicuramente non ti annoierai :) Per rafforzare questo materiale didattico, ti consiglio di guardare questo eccellente video sulla notazione O grande su YouTube. Ci vediamo alle prossime lezioni! :)
GO TO FULL VERSION