Algorithmic complexity

Hi! Today's lesson will be slightly different from the rest. It will differ in that it is only indirectly related to Java. That said, this topic is very important for every programmer. We're going to talk about algorithms. What is an algorithm? In simple terms, it is some sequence of actions that must be completed to achieve a desired result. We use algorithms often in everyday life. For example, every morning you have a specific task: go to school or work, and at the same time be:

• Clothed
• Clean
• Fed

What algorithm lets you achieve this result?

1. Wake up using an alarm clock.
2. Take a shower and wash yourself.
3. Make breakfast and some coffee or tea.
4. Eat.
5. If you didn't iron your clothes the previous evening, then iron them.
6. Get dressed.
7. Leave the house.

This sequence of actions will definitely let you get the desired result. In programming, we are constantly working to complete tasks. A significant portion of these tasks can be performed using algorithms that are already known. For example, suppose your task is to this: sort a list of 100 names in an array. This task is quite simple, but it can be solved in different ways. Here is one possible solution: Algorithm for sorting names alphabetically:

1. Buy or download the 1961 edition of Webster's Third New International Dictionary.
2. Find every name from our list in this dictionary.
3. On a piece of paper, write the page of the dictionary on which the name is located.
4. Use the pieces of paper to sort the names.

Will such a sequence of actions accomplish our task? Yes, it certainly will. Is this solution efficient? Hardly. Here we come to another very important aspects of algorithms: their efficiency. There are several ways to accomplish this task. But both in programming and in ordinary life, we want to choose the most efficient way. If your task is to make a buttered piece of toast, you could start by sowing wheat and milking a cow. But that would be an inefficient solution — it will take a lot of time and will cost a lot of money. You can accomplish your simple task by simply buying bread and butter. Though it does let you to solve the problem, the algorithm involving wheat and a cow is too complex to use in practice. In programming, we have special notation called big O notation to assess the complexity of algorithms. Big O makes it possible to assess how much an algorithm's execution time depends on the input data size. Let's look at the simplest example: data transfer. Imagine that you need to send some information in the form of a file over a long distance (for example, 5000 miles). What algorithm would be most efficient? It depends on the data you are working with. For example, suppose we have an audio file that is 10 MB. In this case, the most efficient algorithm is to send the file over the Internet. It couldn't take more than a couple of minutes! Let's restate our algorithm: "If you want to transfer information in the form of files over a distance of 5000 miles, you should send the data via the Internet". Excellent. Now let's analyze it. Does it accomplish our task? Well, yes, it does. But what can we say about its complexity? Hmm, now things are getting more interesting. The fact is that our algorithm is very dependent on the input data, namely, the size of the files. If we have 10 megabytes, then everything is fine. But what if we need to send 500 megabytes? 20 gigabytes? 500 terabytes? 30 petabytes? Will our algorithm stop working? No, all these amounts of data can indeed be transferred. Will it take longer? Yes, it will! Now we know an important feature of our algorithm: the larger the amount of data to send, the longer it will take to run the algorithm. But we would like to have a more precise understanding of this relationship (between the input data size and the time required to send it). In our case, the algorithmic complexity is linear. "Linear" means that as the amount of input data increases, the time it takes to send it will increase approximately proportionally. If the amount of data doubles, then the time required to send it will be twice as much. If the data increases by 10 times, then the transmission time will increase 10 times. Using big O notation, the complexity of our algorithm is expressed as O(n). You should remember this notation for the future — it is always used for algorithms with linear complexity. Note that we are not talking about several things that may vary here: Internet speed, our computer's computational power, and so on. When assessing the complexity of an algorithm, it simply doesn't make sense to consider these factors — in any event, they are outside our control. Big O notation expresses the complexity of the algorithm itself, not the "environment" that it runs in. Let's continue with our example. Suppose that we ultimately learn that we need to send files totaling 800 terabytes. We can, of course, accomplish our task by sending them over the Internet. There's just one problem: at standard household data transmission rates (100 megabits per second), it will take approximately 708 days. Almost 2 years! :O Our algorithm is obviously not a good fit here. We need some other solution! Unexpectedly, IT giant Amazon comes to our rescue! Amazon's Snowmobile service lets us upload a large amount of data to mobile storage and then deliver it to the desired address by truck! So, we have a new algorithm! "If you want to transfer information in the form of files over a distance of 5000 miles and doing so would take more than 14 days to send via the Internet, you should send the data on an Amazon truck." We chose 14 days arbitrarily here. Let's say this is the longest period we can wait. Let's analyze our algorithm. What about its speed? Even if the truck travels at only 50 mph, it will cover 5000 miles in just 100 hours. This is a little over four days! This is much better than the option of sending the data over the Internet. And what about the complexity of this algorithm? Is it also linear, i.e. O(n)? No, it is not. After all, the truck doesn't care how heavily you load it — it will still drive at about the same speed and arrive on time. Whether we have 800 terabytes, or 10 times that, the truck will still reach its destination within 5 days. In other words, the truck-based data transfer algorithm has constant complexity. Here, "constant" means that it does not depend on the input data size. Put a 1GB flash drive in the truck, it will arrive within 5 days. Put in disks containing 800 terabytes of data, it will arrive within 5 days. When using big O notation, constant complexity is denoted by O(1). We've become familiar with O(n) and O(1), so now let's look at more examples in the world of programming :) Suppose you are given an array of 100 numbers, and the task is to display each of them on the console. You write an ordinary for loop that performs this task

int[] numbers = new int[100];
// ...fill the array with numbers

for (int i: numbers) {
   System.out.println(i);
}

What is the complexity of this algorithm? Linear, i.e. O(n). The number of actions that the program must perform depends on how many numbers are passed to it. If there are 100 numbers in the array, there will be 100 actions (statements to display strings on the screen). If there are 10,000 numbers in the array, then 10,000 actions must be performed. Can our algorithm be improved in any way? No. No matter what, we will have to make N passes through the array and execute N statements to display strings on the console. Consider another example.

public static void main(String[] args) {

   LinkedList<Integer> numbers = new LinkedList<>();
   numbers.add(0, 20202);
   numbers.add(0, 123);
   numbers.add(0, 8283);
}

We have an empty LinkedList into which we insert several numbers. We need to evaluate the algorithmic complexity of inserting a single number into the LinkedList in our example, and how it depends on the number of elements in the list. The answer is O(1), i.e. constant complexity. Why? Note that we insert each number at the beginning of the list. In addition, you will recall that when you insert a number into a LinkedList, the elements don't move anywhere. The links (or references) are updated (if you forgot how LinkedList works, look at one of our old lessons). If the first number in our list is x, and we insert the number y at the front of the list, then all we need to do is this:

x.previous  = y;
y.previous = null;
y.next = x;

When we update the links, we don't care how many numbers are already in the LinkedList, whether one or one billion. The complexity of the algorithm is constant, i.e. O(1).

Logarithmic complexity

Don't panic! :) If the word "logarithmic" makes you want to close this lesson and stop reading, just hold on for a couple of minutes. There won't be any crazy math here (there are plenty of explanations like that elsewhere), and we will pick apart each example. Imagine that your task is to find one specific number in an array of 100 numbers. More precisely, you need to check whether it is there or not. As soon as the required number is found, the search ends, and you display the following in the console: "The required number was found! Its index in the array = ...." How would you accomplish this task? Here the solution is obvious: you need to iterate over the elements of the array one by one, starting from the first (or from the last) and check whether the current number matches the one you are looking for. Accordingly, the number of actions directly depends on the number of elements in the array. If we have 100 numbers, then we could potentially need to go to the next element 100 times and perform 100 comparisons. If there are 1000 numbers, then there could be 1000 comparisons. This is obviously linear complexity, i.e. O(n). And now we'll add one refinement to our example: the array where you need to find the number is sorted in ascending order. Does this change anything in regards to our task? We could still perform a brute-force search for the desired number. But alternatively, we could use the well-known binary s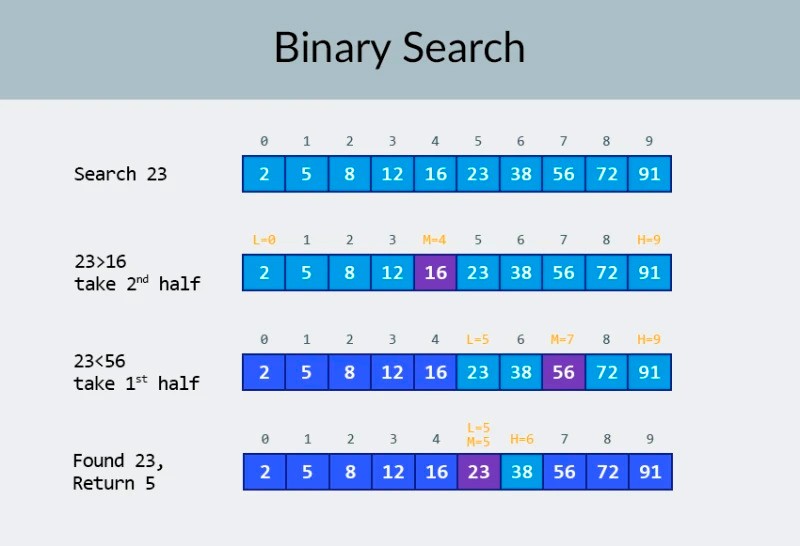earch algorithm. In the top row in the image, we see a sorted array. We need to find the number 23 in it. Instead of iterating over the numbers, we simply divide the array into 2 parts and check the middle number in the array. Find the number that is located in cell 4 and check it (second row in the image). This number is 16, and we are looking for 23. The current number is less that what we are looking for. What does that mean? It means that all the previous numbers (those located before the number 16) don't need to be checked: they are guaranteed to be less than the one we are looking for, because our array is sorted! We continue the search among the remaining 5 elements. Note: we've performed just one comparison, but we have already eliminated half of the possible options. We have only 5 elements left. We will repeat our previous step by once again dividing the remaining subarray in half and again taking the middle element (the 3rd row in the image). The number is 56, and it is larger than the one we are looking for. What does that mean? It means that we have eliminated another 3 possibilities: the number 56 itself as well as the two numbers after it (since they are guaranteed to be greater than 23, because the array is sorted). We only have 2 numbers left to check (the last row in the image) — the numbers with array indices 5 and 6. We check the first of them, and find what we were looking for — the number 23! Its index is 5! Let's look at the results of our algorithm, and then we'll analyze its complexity. By the way, now you understand why this is called binary search: it relies on repeatedly dividing the data in half. The result is impressive! If we used a linear search to look for the number, we would need up to 10 comparisons, but with a binary search, we accomplished the task with only 3! In the worst case, there would be 4 comparisons (if in the last step the number we wanted was the second of the remaining possibilities, rather than the first. So what about its complexity? This is a very interesting point :) The binary search algorithm is much less dependent on the number of elements in the array than the linear search algorithm (that is, simple iteration). With 10 elements in the array, a linear search will need a maximum of 10 comparisons, but a binary search will need a maximum of 4 comparisons. That's a difference by a factor of 2.5. But for an array of 1000 elements, a linear search will need up to 1000 comparisons, but a binary search would require only 10! The difference is now 100 fold! Note: the number of elements in the array has increased 100 times (from 10 to 1000), but the number of comparisons required for a binary search has increased by a factor of only 2.5 (from 4 to 10). If we get to 10,000 elements, the difference will be even more impressive: 10,000 comparisons for linear search, and a total of 14 comparisons for binary search. And again, if the number of elements increases by 1000 times (from 10 to 10000), then the number of comparisons increases by a factor of only 3.5 (from 4 to 14). The complexity of the binary search algorithm is logarithmic, or, if we use big O notation, O(log n). Why is it called that? The logarithm is like the opposite of exponentiation. The binary logarithm is the power to which the number 2 must be raised to obtain a number. For example, we have 10,000 elements that we need to search using the binary search algorithm. 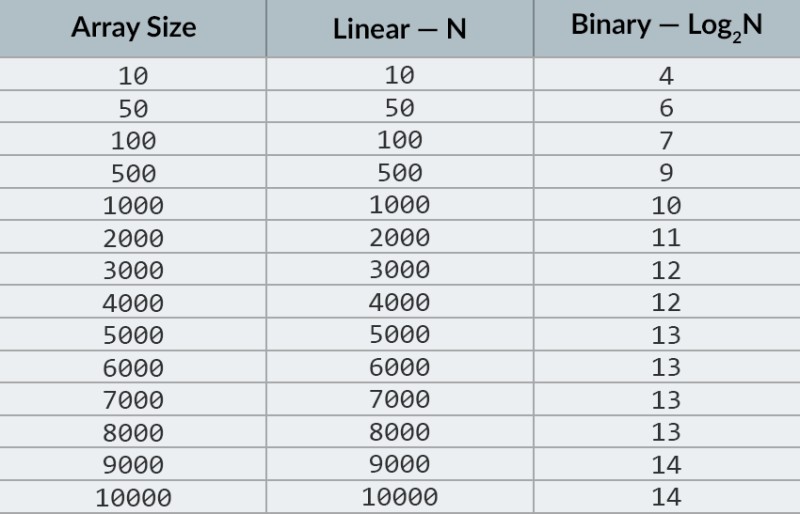Currently, you can look at the table of values to know that doing this will require a maximum of 14 comparisons. But what if nobody has provided such a table and you need to calculate the exact maximum number of comparisons? You just need to answer a simple question: to what power do you need to raise the number 2 so that the result is greater than or equal to the number of elements to be checked? For 10,000, it is the 14th power. 2 to the 13th power is too small (8192), but 2 to the 14th power = 16384, and this number satisfies our condition (it is greater than or equal to the number of elements in the array). We found the logarithm: 14. That's how many comparisons we might need! :) Algorithms and algorithmic complexity is too broad a topic to fit into one lesson. But knowing it is very important: many job interviews will involve questions involving algorithms. For theory, I can recommend some books for you. You can start with " Grokking Algorithms". The examples in this book are written in Python, but the book uses very simple language and examples. It's best option for a beginner and, what's more, it's not very big. Among more serious reading, we have books by Robert Lafore and Robert Sedgewick. Both are written in Java, which will make learning a little easier for you. After all, you are quite familiar with this language! :) For students with good math skills, the best option is Thomas Cormen's book. But theory alone won't fill your belly! Knowledge != Ability. You can practice solving problems involving algorithms on HackerRank and LeetCode. Tasks from these websites are often used even during interviews at Google and Facebook, so you definitely won't be bored :) To reinforce this lesson material, I recommend that you watch this excellent video about big O notation on YouTube. See you in the next lessons! :)