Algoritma telusuran sing beda-beda disesuaikan kanggo tugas sing beda-beda. Dina iki kita bakal ngomong babagan telusuran A *, salah sawijining algoritma patelusuran sing paling efektif. Iki cocog banget kanggo game komputer lan nggawe grafik telusuran kayata cara antarane kutha lan liya-liyane. Sampeyan bisa uga wis ngeweruhi, contone, ing video game strategis utawa taktik, carane sawise menet tombol, pamuter utawa grup langsung miwiti tanpa wektu tundha kanggo pindhah tengen lapangan kanggo titik sing ditemtokake. Ora ana wektu tundha amarga game kasebut nggunakake algoritma efektif sing ngetung persis carane pemain kudu tekan ngendi wae. Utawa mungsuh sing unmistakably nemokake pamuter lan wiwit lumaku ing arah tengen saka kadohan. Biasane, algoritma A * digunakake kanggo tumindak kasebut.
Apa algoritma A *
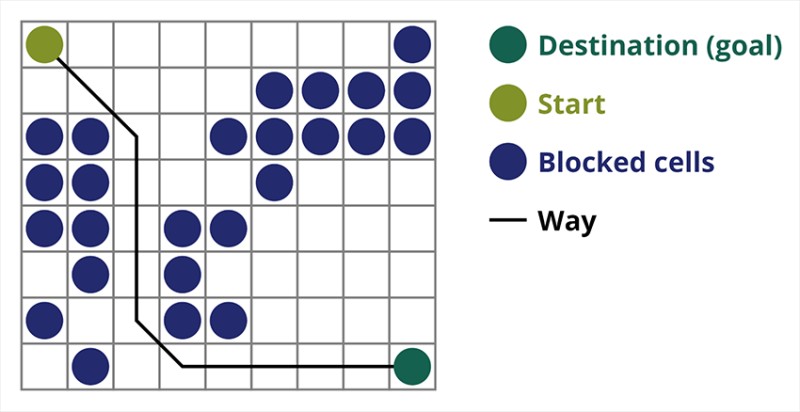
Algoritma Pathfinding A* minangka conto algoritma telusuran paling apik. Tujuan saka algoritma A * yaiku nemokake path saka titik siji menyang titik liyane. Iki minangka salah sawijining klasik kanggo nggoleki algoritma grafik. Ayo ngerteni cara kerjane nggunakake conto. Mbayangno game 2D kanthi tampilan ndhuwur-mudhun. Ayo dibagi area game dadi rakus persegi, contone 8 * 8 sel kaya papan catur. Sel kita bisa dadi salah siji saka rong jinis, bisa dilewati utawa ora bisa dilewati (halangan). Saben wektu pemain utawa mungsuh sing nyedhaki pamuter gerakane siji sel. Ing game, sel passable bisa beda-beda, contone, dalan warata, suket utawa wedhi, kang nemtokake kangelan kanggo mindhah bebarengan, nanging kanggo gamblang kita bakal nganggep kabeh sel passable liwati ing cara sing padha. Ing gambar ing ngisor iki, sel biru minangka alangan.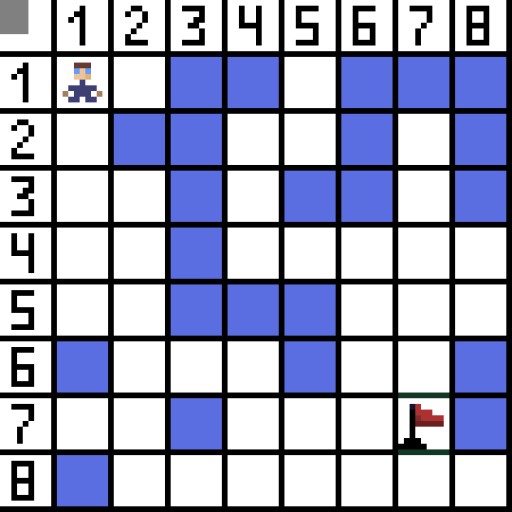
Ayo nemtokake siji sel (utawa simpul) minangka sel wiwitan (karakter kasebut ana), lan sel liyane minangka target utawa sel gol (sing duwe gendera), lan njlèntrèhaké cara algoritma A * kanggo kasus iki. Karakter ana ing sel (1,1) lan target ana ing sel (7,7). Saben sel nduweni tetanggan horisontal, vertikal, lan diagonal. Iku gumantung ing game, yen kita ngetung kelenjar diagonal utawa ora. Contone ing akeh game tampilan ndhuwur-mudhun kayata Bomberman utawa Pacman karakter bisa mindhah mung horisontal utawa vertikal. Ing kasus iki saben simpul, kajaba ndemek pinggiran, mung 4 tanggi. Yen kita ngomong bab game ngendi karakter bisa mindhah diagonal, saben simpul bisa duwe nganti 8 tanggi. Ing langkah pisanan saka algoritma, sel ing ngendi karakter dumunung duwe loro tetanggan. Luwih tepate, telu, nanging siji saka wong-wong mau minangka alangan. 
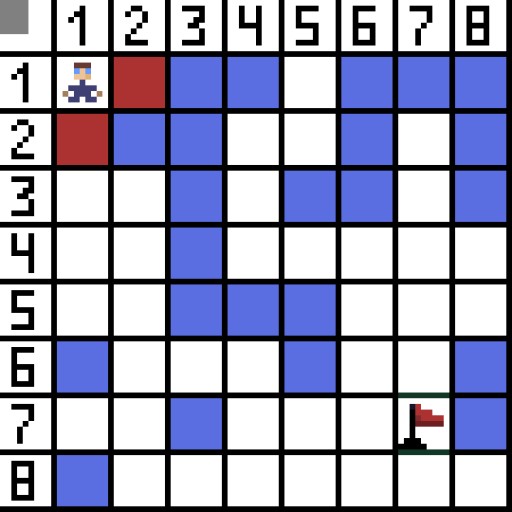Cetha yen cara diagonal luwih dawa. yen kita nyetel sisih sel kita dadi kondisional padha karo siji, banjur dawa diagonal sel iki padha karo akar kuadrat saka loro. Iki minangka teorema Pythagoras. Kanggo pindhah saka sel A menyang sel B, sampeyan kudu milih salah siji saka sel tetanggan, banjur sel sabanjure, lan sateruse. Uga, ing sadawane dalan, ngerti apa sampeyan bisa pindhah saka sel dhisikan menyang target. Algoritma A * ing saben langkah milih salah siji saka sel tetanggan sesuai karo nilai fungsi F. Fungsi iki ngukur carane sel calon apik kanggo kalebu ing dalan paling cedhak kita. Iki minangka fungsi biaya, lan iku jumlah saka fungsi pamindhahan G lan fungsi heuristik.
-
G biaya - punika kadohan saka simpul wiwitan.
-
Biaya H (Heuristik) yaiku jarak saka titik pungkasan (tujuan). Fungsi iki bisa beda-beda, pangembang mutusake apa sing luwih apik. Mbok pilihan saka H paling penting ing A *, lan iki titik sing ndadekake sembarang implementasine tartamtu saka algoritma luwih utawa kurang efektif. Secara teoritis sampeyan bisa nggunakake fungsi apa wae sing dikarepake.
Ing kasus kita, kita ngerti posisi sel target lan bisa, contone, ngetung jarak Euclidean geometris antarane target lan sel saiki. Sing luwih cendhek jarak, luwih cedhak karo tujuan.
-
F biaya = G + H. Dadi algoritma ngetung kabeh simpul pepadhamu F biaya lan milih salah siji saka paling F biaya dipikir pisanan. Nalika kita milih salah siji kita menehi tandha minangka ditutup lan ngetung nilai kanggo tanggi simpul iki.
Fungsi heuristik Kepiye cara ngetung H?
Iki minangka fungsi heuristik. Jeneng kasebut dhewe tegese ditemtokake dening pengalaman, lan bisa uga beda. Ing kene kita bakal njupuk padha karo sing diarani jarak Euclidean antarane titik (x1, y1) lan (x2, y2):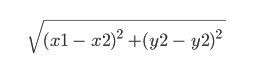
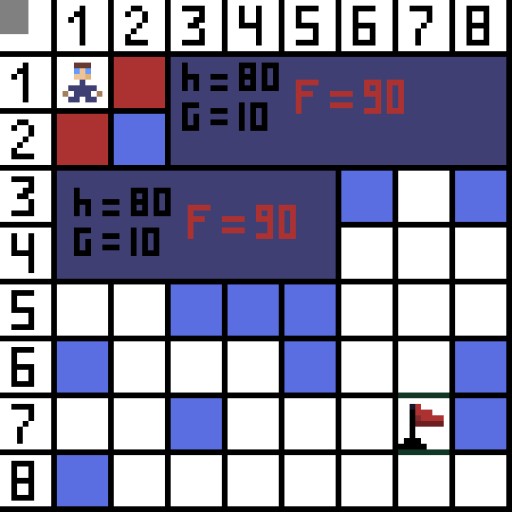Ing gambar, kanggo langkah pisanan, ana rong pilihan, lan padha karo biaya, nanging ing langkah sabanjure, karakter nemu menyang buntu ing salah siji opsi. Mulane, kita arep dalan liyane. Ing pengulangan sabanjure, kita wis duwe 4 opsi. 
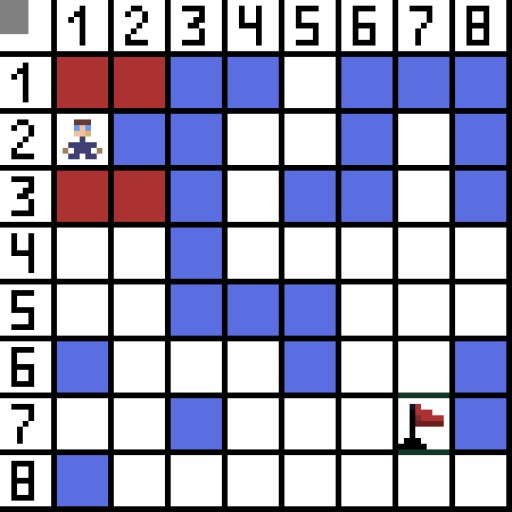Loro mau ora cocok, amarga padha mimpin mundur, lan opsi liyane padha apik, nanging algoritma mutusaké sing paling apik kanggo pindhah diagonally menyang sel (3,2). Salajengipun, ing saben langkah, pitungan fungsi F diulang nganti karakter tekan sel target. Yen, mesthi, wacana kuwi ana. 
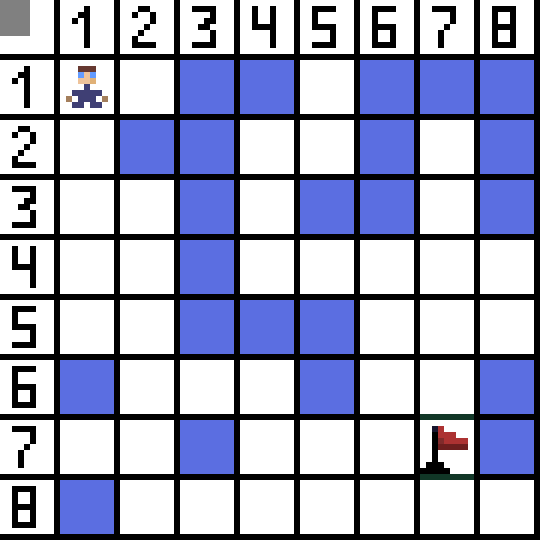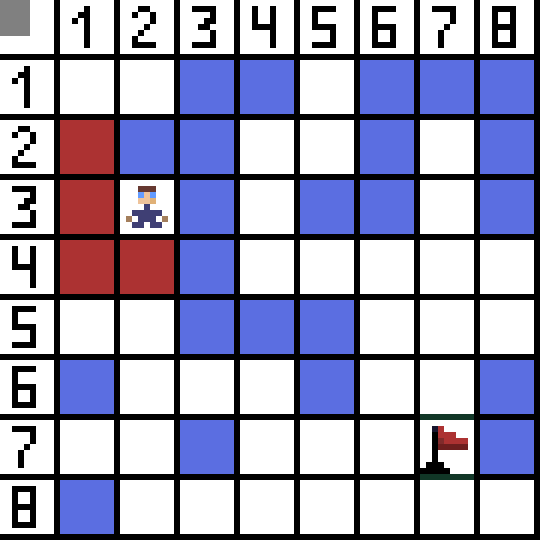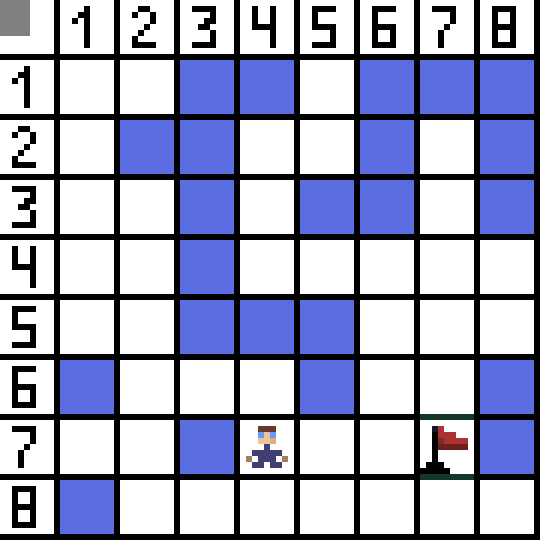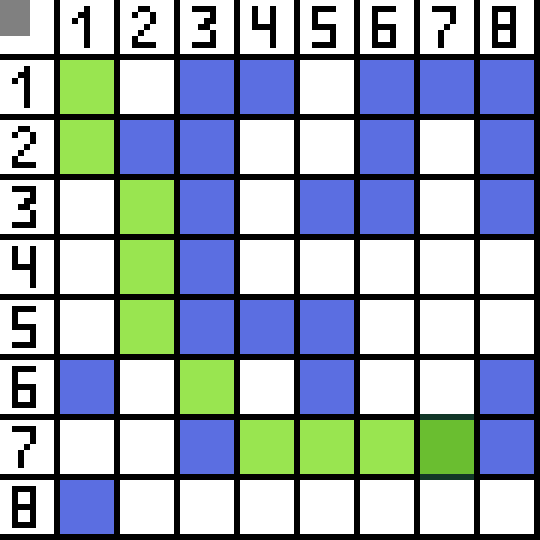Cara ijo ing gif-gambar nuduhake path optimal karakter kanggo gendéra.
A* Algoritma langkah demi langkah
Kanggo ngleksanakake algoritma ing Jawa, sampeyan kudu njupuk langkah-langkah ing ngisor iki 1. Pisanan sampeyan kudu nggawe rong dhaptar, kanggo simpul mbukak lan simpul tertutup. 2. Initialize loro dhaptar. Ing dhaptar sing ditutup, simpul wiwitan nuduhake dhaptar sing mbukak. 3. dene ana unsur ing daftar buka: 3a. Temokake simpul min kanthi F 3b paling cilik. Mbusak min saka dhaptar mbukak 3c. Nemtokake tanggi min (nganti 8, yen diagonal dijupuk menyang akun) 3d. Priksa saben pepadhamu: a) yen pepadhamu iku sel target, mungkasi nggoleki b) Yen ora, ngitung G, H kanggo iku. G = min.G + jarak antarane pepadhamu lan min F = G + H c) yen simpul kanthi posisi sing padha karo pepadhamu ana ing daftar mbukak lan F kurang saka tetanggan, skip pepadhamu kasebut d) yen simpul karo posisi padha pepadhamu ing dhaftar ditutup, lan f kurang saka pepadhamu, skip pepadhamu sing. Yen ora, tambahake simpul menyang dhaptar mbukak Pungkasan daur ulang batin 3e. Nambahake min menyang dhaptar tertutup Pungkasan loop njaba Dadi, ing saben pengulangan kita bakal nindakake sabanjure:- Pilih sel saka dhaptar sing mbukak kanthi skor total sing paling murah.
- Mbusak sel iki saka dhaptar sing mbukak.
- Tambahake kabeh sel sing bisa digayuh menyang dhaptar sing mbukak.
- Nalika nindakake iki, kita uga ngolah skor anyar saka simpul kasebut menyang saben sing anyar kanggo ndeleng manawa ana paningkatan apa sing wis ana, lan yen ana, kita nganyari apa sing dingerteni babagan sel kasebut.
A* Pseudocode
Punika pseudocode singkat A* pathfinding:Input: a grid with locked and empty cells, with start and goal cell.
Output: least cost path from start to goal cell.
Initialisation
openList = {startCell} //list of traversed cells
closedList = {} //list of already traversed cells
g.startCell = 0 //cost from source cell to a cell
h.startCell = h(startCell, goal) //heuristic
f.startCell = g.startCell + h.StartCell
while openList is not empty
do
//let the currentCell equal the cell with the least f value
currentCell = Cell on top of openList, with least f
if currentCell == end return
remove currentCell from openList
add currentCell to closedList
foreach n in child.currentCell
if n in closedList
continue
cost = g.currentCell + distance(currentCell,n)
if (n in openList and cost < g.n)
remove n from closedList
g.n = cost
h.n = h(n, goal)
f.n = g.n + h.nSaka pseudocode nganti A* Implementasi ing Jawa
A* Pathfinding ing realisasi Jawa kudu duwe sawetara cara kanggo ngladeni algoritma:- Sel, struktur kanggo nahan paramèter sing dibutuhake
- Dhaptar mbukak lan ditutup
- Metode kanggo ngitung fungsi heuristik
- Cara kanggo nglacak dalan saka sumber menyang tujuan
- Cara kanggo mriksa yen sel sing diwenehake diblokir, yen wis tekan, yen bener lan liya-liyane
package Asterist;
import java.util.PriorityQueue;
import java.util.Stack;
public class AAsterisk {
//Java Program to implement A* Search Algorithm
//Here we're creating a shortcut for (int, int) pair
public static class Pair {
int first;
int second;
public Pair(int first, int second){
this.first = first;
this.second = second;
}
@Override
public boolean equals(Object obj) {
return obj instanceof Pair && this.first == ((Pair)obj).first && this.second == ((Pair)obj).second;
}
}
// Creating a shortcut for tuple<int, int, int> type
public static class Details {
double value;
int i;
int j;
public Details(double value, int i, int j) {
this.value = value;
this.i = i;
this.j = j;
}
}
// a Cell (node) structure
public static class Cell {
public Pair parent;
// f = g + h, where h is heuristic
public double f, g, h;
Cell()
{
parent = new Pair(-1, -1);
f = -1;
g = -1;
h = -1;
}
public Cell(Pair parent, double f, double g, double h) {
this.parent = parent;
this.f = f;
this.g = g;
this.h = h;
}
}
// method to check if our cell (row, col) is valid
boolean isValid(int[][] grid, int rows, int cols,
Pair point)
{
if (rows > 0 && cols > 0)
return (point.first >= 0) && (point.first < rows)
&& (point.second >= 0)
&& (point.second < cols);
return false;
}
//is the cell blocked?
boolean isUnBlocked(int[][] grid, int rows, int cols,
Pair point)
{
return isValid(grid, rows, cols, point)
&& grid[point.first][point.second] == 1;
}
//Method to check if destination cell has been already reached
boolean isDestination(Pair position, Pair dest)
{
return position == dest || position.equals(dest);
}
// Method to calculate heuristic function
double calculateHValue(Pair src, Pair dest)
{
return Math.sqrt(Math.pow((src.first - dest.first), 2.0) + Math.pow((src.second - dest.second), 2.0));
}
// Method for tracking the path from source to destination
void tracePath(
Cell[][] cellDetails,
int cols,
int rows,
Pair dest)
{ //A* Search algorithm path
System.out.println("The Path: ");
Stack<Pair> path = new Stack<>();
int row = dest.first;
int col = dest.second;
Pair nextNode = cellDetails[row][col].parent;
do {
path.push(new Pair(row, col));
nextNode = cellDetails[row][col].parent;
row = nextNode.first;
col = nextNode.second;
} while (cellDetails[row][col].parent != nextNode); // until src
while (!path.empty()) {
Pair p = path.peek();
path.pop();
System.out.println("-> (" + p.first + "," + p.second + ") ");
}
}
// A main method, A* Search algorithm to find the shortest path
void aStarSearch(int[][] grid,
int rows,
int cols,
Pair src,
Pair dest)
{
if (!isValid(grid, rows, cols, src)) {
System.out.println("Source is invalid...");
return;
}
if (!isValid(grid, rows, cols, dest)) {
System.out.println("Destination is invalid...");
return;
}
if (!isUnBlocked(grid, rows, cols, src)
|| !isUnBlocked(grid, rows, cols, dest)) {
System.out.println("Source or destination is blocked...");
return;
}
if (isDestination(src, dest)) {
System.out.println("We're already (t)here...");
return;
}
boolean[][] closedList = new boolean[rows][cols];//our closed list
Cell[][] cellDetails = new Cell[rows][cols];
int i, j;
// Initialising of the starting cell
i = src.first;
j = src.second;
cellDetails[i][j] = new Cell();
cellDetails[i][j].f = 0.0;
cellDetails[i][j].g = 0.0;
cellDetails[i][j].h = 0.0;
cellDetails[i][j].parent = new Pair( i, j );
// Creating an open list
PriorityQueue<Details> openList = new PriorityQueue<>((o1, o2) -> (int) Math.round(o1.value - o2.value));
// Put the starting cell on the open list, set f.startCell = 0
openList.add(new Details(0.0, i, j));
while (!openList.isEmpty()) {
Details p = openList.peek();
// Add to the closed list
i = p.i; // second element of tuple
j = p.j; // third element of tuple
// Remove from the open list
openList.poll();
closedList[i][j] = true;
// Generating all the 8 neighbors of the cell
for (int addX = -1; addX <= 1; addX++) {
for (int addY = -1; addY <= 1; addY++) {
Pair neighbour = new Pair(i + addX, j + addY);
if (isValid(grid, rows, cols, neighbour)) {
if(cellDetails[neighbour.first] == null){ cellDetails[neighbour.first] = new Cell[cols]; }
if (cellDetails[neighbour.first][neighbour.second] == null) {
cellDetails[neighbour.first][neighbour.second] = new Cell();
}
if (isDestination(neighbour, dest)) {
cellDetails[neighbour.first][neighbour.second].parent = new Pair ( i, j );
System.out.println("The destination cell is found");
tracePath(cellDetails, rows, cols, dest);
return;
}
else if (!closedList[neighbour.first][neighbour.second]
&& isUnBlocked(grid, rows, cols, neighbour)) {
double gNew, hNew, fNew;
gNew = cellDetails[i][j].g + 1.0;
hNew = calculateHValue(neighbour, dest);
fNew = gNew + hNew;
if (cellDetails[neighbour.first][neighbour.second].f == -1
|| cellDetails[neighbour.first][neighbour.second].f > fNew) {
openList.add(new Details(fNew, neighbour.first, neighbour.second));
// Update the details of this
// cell
cellDetails[neighbour.first][neighbour.second].g = gNew;
//heuristic function cellDetails[neighbour.first][neighbour.second].h = hNew;
cellDetails[neighbour.first][neighbour.second].f = fNew;
cellDetails[neighbour.first][neighbour.second].parent = new Pair( i, j );
}
}
}
}
}
}
System.out.println("Failed to find the Destination Cell");
}
// test
public static void main(String[] args) {
//0: The cell is blocked
// 1: The cell is not blocked
int[][] grid = {
{ 1, 1, 0, 0, 1, 0, 0, 0 },
{ 1, 0, 0, 1, 1, 0, 1, 0 },
{ 1, 1, 0, 1, 0, 0, 1, 0 },
{ 1, 1, 0, 1, 1, 1, 1, 1 },
{ 1, 1, 0, 0, 0, 1, 1, 1 },
{ 0, 1, 1, 1, 0, 1, 1, 0 },
{ 1, 1, 0, 1, 1, 1, 1, 0 },
{ 0, 1, 1, 1, 1, 1, 1, 1 }
};
// Start is the left-most upper-most corner
Pair src = new Pair(0,0);
//(8, 0);
// Destination is the right-most bottom-most corner
Pair dest = new Pair(6, 6);
AAsterisk app = new AAsterisk();
app.aStarSearch(grid, grid.length , grid[0].length, src, dest);
}
}
Path: -> (0,0) -> (1,0) -> (2,1) -> (3,1) -> (4,1) -> (5,2) -> (5, 3) -> (6,4) -> (6,5) -> (6,6)
Bisa dideleng manawa iki minangka salah sawijining dalan paling cendhak sing bisa dibangun ing antarane rong titik kasebut. Elinga yen langkah kaping enem ing conto kita ing gambar lan ing output program beda-beda, sanajan dalan dadi padha efektif. Program milih salah siji saka akeh opsi paling efektif.
GO TO FULL VERSION