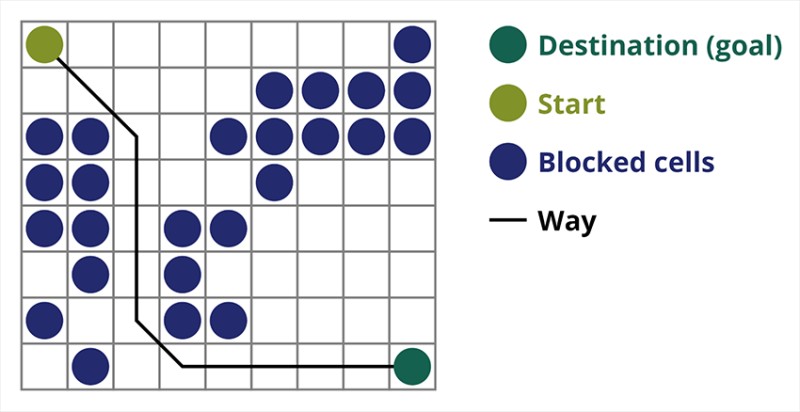
Diferentes algoritmos de pesquisa são adaptados para diferentes tarefas. Hoje vamos falar sobre a pesquisa A*, um dos algoritmos de localização de caminhos mais eficazes. Este é muito adequado para jogos de computador e construção de gráficos de busca, como caminhos entre cidades e assim por diante. Você deve ter notado, por exemplo, em videogames estratégicos ou táticos, como após pressionar um botão, seu jogador ou grupo começa imediatamente, sem demora, a atravessar o campo até o ponto que você especificou. Não há atraso justamente porque os jogos utilizam algoritmos eficazes que calculam exatamente como o jogador precisa chegar a algum lugar. Ou um inimigo que encontra o jogador com precisão e começa a caminhar na direção certa de longe. Normalmente, o algoritmo A* é usado para tais ações.
O que é algoritmo A*
O algoritmo Pathfinding A* é um exemplo de algoritmo de busca do melhor primeiro. O objetivo do algoritmo A* é encontrar um caminho de um ponto a outro. É um dos clássicos para pesquisar algoritmos de grafos. Vamos descobrir como funciona usando um exemplo. Imagine um jogo 2D com visão de cima para baixo. Vamos dividir nossa área de jogo em ganância quadrada, por exemplo 8*8 células como um tabuleiro de xadrez. Nossas células podem ser de dois tipos: transitáveis ou intransponíveis (obstáculo). Cada período de tempo que um jogador ou inimigo que se aproxima do jogador move uma célula. Nos jogos, as células transitáveis podem ser de natureza diferente, por exemplo, uma estrada plana, grama ou areia, o que determina a dificuldade de movimentação ao longo delas, mas para simplificar, assumiremos que todas as células transitáveis são passadas da mesma maneira. Na imagem abaixo, as células azuis são obstáculos.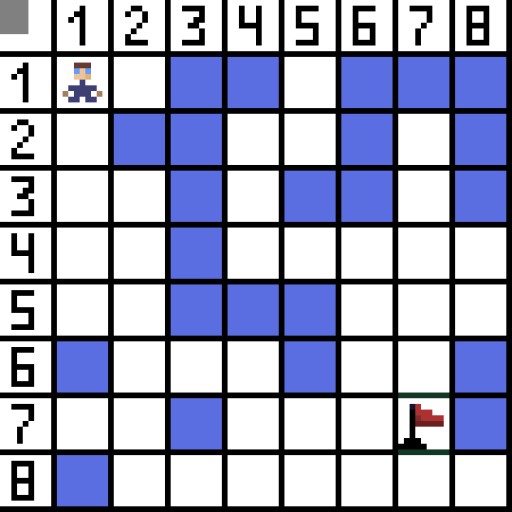
Vamos atribuir uma célula (ou nó) como célula inicial (o caractere está nela) e a outra célula como célula alvo ou meta (aquela com o sinalizador) e descrever como o algoritmo A* funciona para este caso. O personagem está na célula (1,1) e o alvo está na célula (7,7). Cada célula possui vizinhos horizontais, verticais e diagonais. Depende do jogo se calculamos nós diagonais ou não. Por exemplo, em muitos jogos com visão de cima para baixo, como Bomberman ou Pacman, os personagens só podem se mover horizontalmente ou verticalmente. Neste caso, cada nó, exceto o que toca nas arestas, possui apenas 4 vizinhos. Se estamos falando de um jogo onde os personagens podem se mover na diagonal, cada nó pode ter até 8 vizinhos. Na primeira etapa do algoritmo, a célula onde o personagem está localizado possui dois vizinhos. Mais precisamente, três, mas um deles é um obstáculo. 
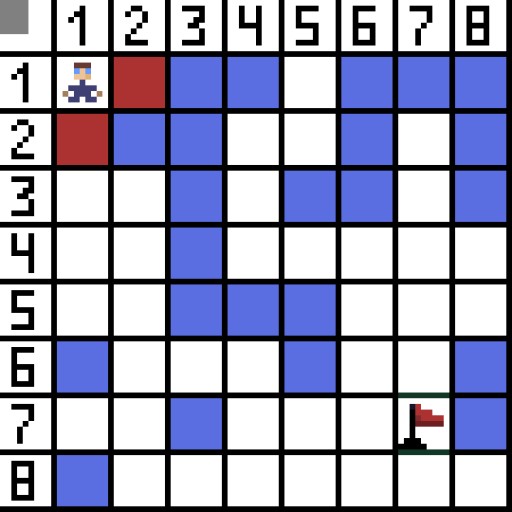É claro que o caminho diagonal é mais longo. se definirmos que o lado da nossa célula é condicionalmente igual a um, então o comprimento da diagonal desta célula é igual à raiz quadrada de dois. Isto é o que diz o teorema de Pitágoras. Para ir da célula A para a célula B, você deve primeiro selecionar uma das células vizinhas, depois a próxima e assim por diante. Além disso, ao longo do caminho, entenda se é possível ir da célula inicial até a célula de destino. O algoritmo A* em cada etapa seleciona uma das células vizinhas de acordo com o valor da função F. Esta função mede quão boa é uma célula candidata para ser incluída em nosso caminho mais curto. Esta é a função de custo e é a soma da função de movimento G e da função heurística.
-
Custo G - é a distância de um nó inicial.
-
O custo H (heurística) é a distância do nó final (objetivo). Esta função pode ser diferente, um desenvolvedor decide o que é melhor. Talvez a escolha de H seja a mais importante em A*, e este é o ponto que torna qualquer implementação particular do algoritmo mais ou menos eficaz. Teoricamente você pode usar qualquer função que desejar.
No nosso caso, conhecemos a posição da célula alvo e podemos, por exemplo, calcular a distância euclidiana geométrica entre a célula alvo e a célula atual. Quanto menor a distância, mais perto estamos do objetivo.
-
Custo F = G + H. Portanto, o algoritmo calcula os custos F de todos os nós vizinhos e escolhe um dos custos F mais baixos para observar primeiro. Quando escolhemos um, marcamos-o como fechado e calculamos os valores para os vizinhos deste nó.
Função heurísticaComo podemos calcular H?
Esta é uma função heurística. O próprio nome significa que é determinado pela experiência e pode ser diferente. Aqui vamos considerá-la igual à chamada distância euclidiana entre os pontos (x1, y1) e (x2, y2):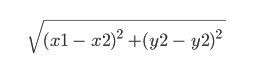
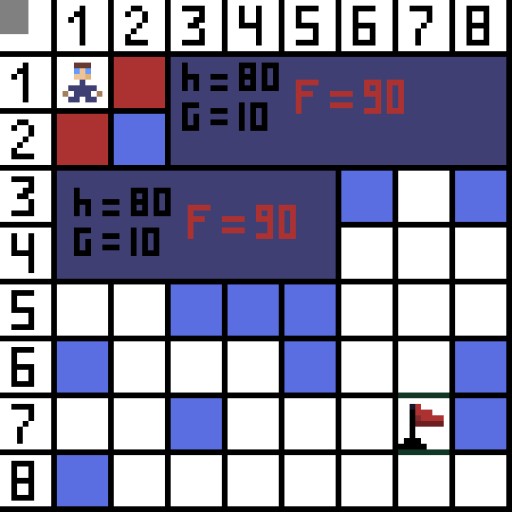Na imagem, para a primeira etapa, existem duas opções, e elas têm o mesmo custo, mas na próxima etapa o personagem chega a um beco sem saída em uma das opções. Portanto, estamos indo para o outro lado. Na próxima iteração, já temos 4 opções. 
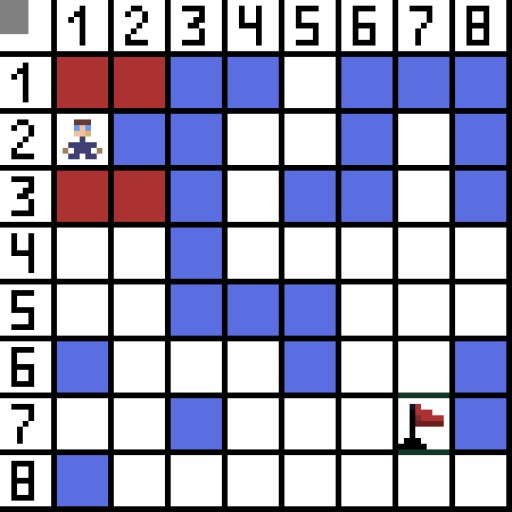Duas delas não são adequadas porque levam para trás, e as outras opções são igualmente boas, mas o algoritmo decidiu que era melhor ir diagonalmente até a célula (3,2). Além disso, em cada etapa, o cálculo da função F é repetido até que o caractere atinja a célula alvo. Se, é claro, tal passagem existir. 
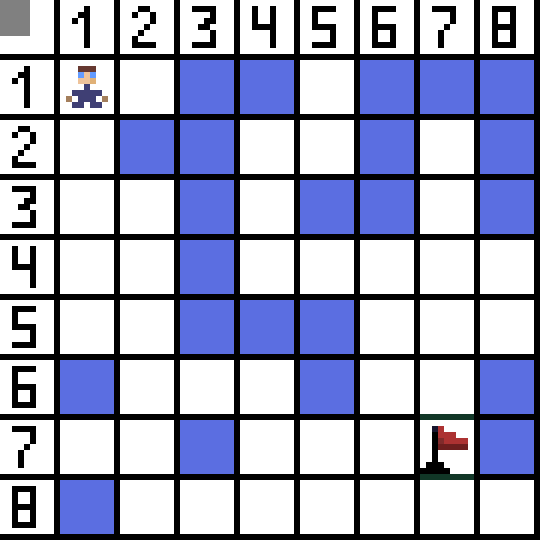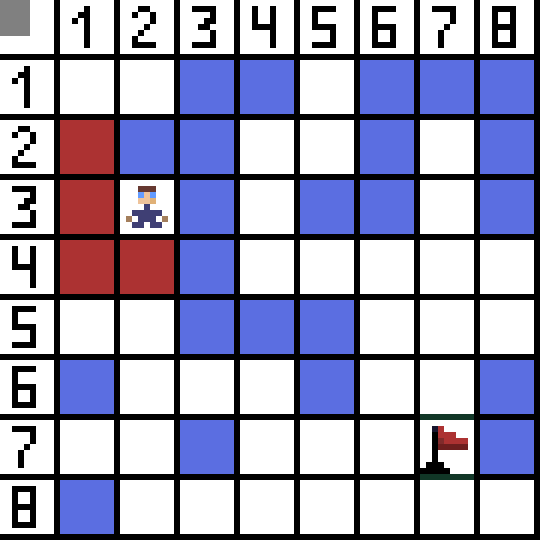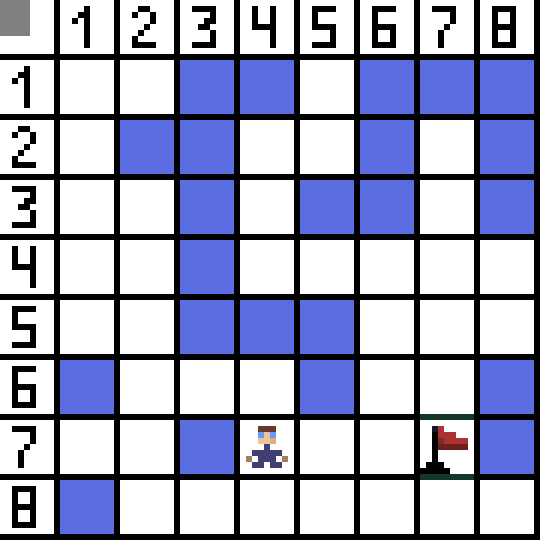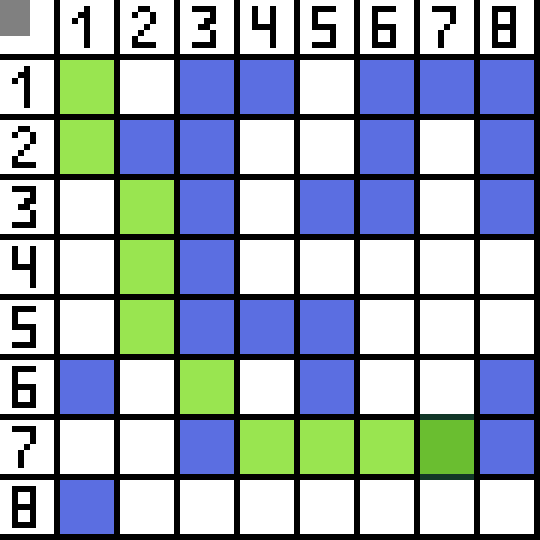O caminho verde na imagem gif indica o caminho ideal do personagem até a bandeira.
A* Algoritmo passo a passo
Para implementar o algoritmo em Java, você precisa seguir os seguintes passos 1. Primeiro você precisa criar duas listas, para nós abertos e nós fechados. 2. Inicialize ambas as listas. Numa lista fechada, o nó inicial aponta para a lista aberta. 3. enquanto houver elementos na lista aberta: 3a. Encontre o nó min com o menor F 3b. Remova min da lista aberta 3c. Determine vizinhos mínimos (até 8, se as diagonais forem levadas em consideração) 3d. Verificando cada vizinho: a) se o vizinho for a célula alvo, pare de pesquisar b) Caso contrário, calcule G, H para ele. G = min.G + distância entre vizinho e min F = G + H c) se o nó com a mesma posição do vizinho estiver na lista aberta e seu F for menor que o do vizinho, pule esse vizinho d) se o nó com a mesma posição do vizinho está na lista fechada e seu f é menor que o do vizinho, pule esse vizinho. Caso contrário, adicione o nó à lista aberta. Fim do loop interno 3e. Adicionando min à lista fechada Fim do loop externo Então, a cada iteração faremos o seguinte:- Selecione a célula da nossa lista aberta com a pontuação total estimada mais baixa.
- Remova esta célula da lista aberta.
- Adicione todas as células que pudermos alcançar à lista aberta.
- Quando fazemos isso, também processamos a nova pontuação desse nó para cada novo para ver se é uma melhoria em relação ao que temos até agora e, se for, atualizamos o que sabemos sobre aquela célula.
A* Pseudocódigo
Aqui está um breve pseudocódigo do pathfinding A*:
Input: a grid with locked and empty cells, with start and goal cell.
Output: least cost path from start to goal cell.
Initialisation
openList = {startCell} //list of traversed cells
closedList = {} //list of already traversed cells
g.startCell = 0 //cost from source cell to a cell
h.startCell = h(startCell, goal) //heuristic
f.startCell = g.startCell + h.StartCell
while openList is not empty
do
//let the currentCell equal the cell with the least f value
currentCell = Cell on top of openList, with least f
if currentCell == end return
remove currentCell from openList
add currentCell to closedList
foreach n in child.currentCell
if n in closedList
continue
cost = g.currentCell + distance(currentCell,n)
if (n in openList and cost < g.n)
remove n from closedList
g.n = cost
h.n = h(n, goal)
f.n = g.n + h.nDo pseudocódigo à implementação A* em Java
A* Pathfinding na realização Java deve ter alguns métodos para servir ao algoritmo:- Célula, uma estrutura para armazenar os parâmetros necessários
- Listas abertas e fechadas
- Método para calcular a função heurística
- Método para rastrear o caminho da origem ao destino
- Métodos para verificar se determinada célula está bloqueada, se já foi alcançada, se é válida e assim por diante
package Asterist;
import java.util.PriorityQueue;
import java.util.Stack;
public class AAsterisk {
//Java Program to implement A* Search Algorithm
//Here we're creating a shortcut for (int, int) pair
public static class Pair {
int first;
int second;
public Pair(int first, int second){
this.first = first;
this.second = second;
}
@Override
public boolean equals(Object obj) {
return obj instanceof Pair && this.first == ((Pair)obj).first && this.second == ((Pair)obj).second;
}
}
// Creating a shortcut for tuple<int, int, int> type
public static class Details {
double value;
int i;
int j;
public Details(double value, int i, int j) {
this.value = value;
this.i = i;
this.j = j;
}
}
// a Cell (node) structure
public static class Cell {
public Pair parent;
// f = g + h, where h is heuristic
public double f, g, h;
Cell()
{
parent = new Pair(-1, -1);
f = -1;
g = -1;
h = -1;
}
public Cell(Pair parent, double f, double g, double h) {
this.parent = parent;
this.f = f;
this.g = g;
this.h = h;
}
}
// method to check if our cell (row, col) is valid
boolean isValid(int[][] grid, int rows, int cols,
Pair point)
{
if (rows > 0 && cols > 0)
return (point.first >= 0) && (point.first < rows)
&& (point.second >= 0)
&& (point.second < cols);
return false;
}
//is the cell blocked?
boolean isUnBlocked(int[][] grid, int rows, int cols,
Pair point)
{
return isValid(grid, rows, cols, point)
&& grid[point.first][point.second] == 1;
}
//Method to check if destination cell has been already reached
boolean isDestination(Pair position, Pair dest)
{
return position == dest || position.equals(dest);
}
// Method to calculate heuristic function
double calculateHValue(Pair src, Pair dest)
{
return Math.sqrt(Math.pow((src.first - dest.first), 2.0) + Math.pow((src.second - dest.second), 2.0));
}
// Method for tracking the path from source to destination
void tracePath(
Cell[][] cellDetails,
int cols,
int rows,
Pair dest)
{ //A* Search algorithm path
System.out.println("The Path: ");
Stack<Pair> path = new Stack<>();
int row = dest.first;
int col = dest.second;
Pair nextNode = cellDetails[row][col].parent;
do {
path.push(new Pair(row, col));
nextNode = cellDetails[row][col].parent;
row = nextNode.first;
col = nextNode.second;
} while (cellDetails[row][col].parent != nextNode); // until src
while (!path.empty()) {
Pair p = path.peek();
path.pop();
System.out.println("-> (" + p.first + "," + p.second + ") ");
}
}
// A main method, A* Search algorithm to find the shortest path
void aStarSearch(int[][] grid,
int rows,
int cols,
Pair src,
Pair dest)
{
if (!isValid(grid, rows, cols, src)) {
System.out.println("Source is invalid...");
return;
}
if (!isValid(grid, rows, cols, dest)) {
System.out.println("Destination is invalid...");
return;
}
if (!isUnBlocked(grid, rows, cols, src)
|| !isUnBlocked(grid, rows, cols, dest)) {
System.out.println("Source or destination is blocked...");
return;
}
if (isDestination(src, dest)) {
System.out.println("We're already (t)here...");
return;
}
boolean[][] closedList = new boolean[rows][cols];//our closed list
Cell[][] cellDetails = new Cell[rows][cols];
int i, j;
// Initialising of the starting cell
i = src.first;
j = src.second;
cellDetails[i][j] = new Cell();
cellDetails[i][j].f = 0.0;
cellDetails[i][j].g = 0.0;
cellDetails[i][j].h = 0.0;
cellDetails[i][j].parent = new Pair( i, j );
// Creating an open list
PriorityQueue<Details> openList = new PriorityQueue<>((o1, o2) -> (int) Math.round(o1.value - o2.value));
// Put the starting cell on the open list, set f.startCell = 0
openList.add(new Details(0.0, i, j));
while (!openList.isEmpty()) {
Details p = openList.peek();
// Add to the closed list
i = p.i; // second element of tuple
j = p.j; // third element of tuple
// Remove from the open list
openList.poll();
closedList[i][j] = true;
// Generating all the 8 neighbors of the cell
for (int addX = -1; addX <= 1; addX++) {
for (int addY = -1; addY <= 1; addY++) {
Pair neighbour = new Pair(i + addX, j + addY);
if (isValid(grid, rows, cols, neighbour)) {
if(cellDetails[neighbour.first] == null){ cellDetails[neighbour.first] = new Cell[cols]; }
if (cellDetails[neighbour.first][neighbour.second] == null) {
cellDetails[neighbour.first][neighbour.second] = new Cell();
}
if (isDestination(neighbour, dest)) {
cellDetails[neighbour.first][neighbour.second].parent = new Pair ( i, j );
System.out.println("The destination cell is found");
tracePath(cellDetails, rows, cols, dest);
return;
}
else if (!closedList[neighbour.first][neighbour.second]
&& isUnBlocked(grid, rows, cols, neighbour)) {
double gNew, hNew, fNew;
gNew = cellDetails[i][j].g + 1.0;
hNew = calculateHValue(neighbour, dest);
fNew = gNew + hNew;
if (cellDetails[neighbour.first][neighbour.second].f == -1
|| cellDetails[neighbour.first][neighbour.second].f > fNew) {
openList.add(new Details(fNew, neighbour.first, neighbour.second));
// Update the details of this
// cell
cellDetails[neighbour.first][neighbour.second].g = gNew;
//heuristic function cellDetails[neighbour.first][neighbour.second].h = hNew;
cellDetails[neighbour.first][neighbour.second].f = fNew;
cellDetails[neighbour.first][neighbour.second].parent = new Pair( i, j );
}
}
}
}
}
}
System.out.println("Failed to find the Destination Cell");
}
// test
public static void main(String[] args) {
//0: The cell is blocked
// 1: The cell is not blocked
int[][] grid = {
{ 1, 1, 0, 0, 1, 0, 0, 0 },
{ 1, 0, 0, 1, 1, 0, 1, 0 },
{ 1, 1, 0, 1, 0, 0, 1, 0 },
{ 1, 1, 0, 1, 1, 1, 1, 1 },
{ 1, 1, 0, 0, 0, 1, 1, 1 },
{ 0, 1, 1, 1, 0, 1, 1, 0 },
{ 1, 1, 0, 1, 1, 1, 1, 0 },
{ 0, 1, 1, 1, 1, 1, 1, 1 }
};
// Start is the left-most upper-most corner
Pair src = new Pair(0,0);
//(8, 0);
// Destination is the right-most bottom-most corner
Pair dest = new Pair(6, 6);
AAsterisk app = new AAsterisk();
app.aStarSearch(grid, grid.length , grid[0].length, src, dest);
}
}
O Caminho: -> (0,0) -> (1,0) -> (2,1) -> (3,1) -> (4,1) -> (5,2) -> (5, 3) -> (6,4) -> (6,5) -> (6,6)
Percebe-se que este é um dos vários caminhos mais curtos que podem ser construídos entre esses dois pontos. Observe que a sexta etapa do nosso exemplo na imagem e na saída do programa é diferente, embora os caminhos tenham se mostrado igualmente eficazes. O programa seleciona uma das muitas opções mais eficazes.
GO TO FULL VERSION