A* Search Algorithm in Java

Different search algorithms are tailored for different tasks. Today we are going to talk about A* search, one of the most effective pathfinding algorithms. This one is very well suited for computer games and building searching graphs such as ways between cities and so on. You may have noticed, for example, in strategic or tactical video games, how after pressing a button, your player or group starts immediately without delay to go across the field to the point you specified. There is no delay precisely because the games use effective algorithms that calculate exactly how the player needs to get somewhere. Or an enemy that unmistakably finds the player and starts walking in the right direction from afar. Usually, the A* algorithm is used for such actions.

What is A* algorithm

Pathfinding algorithm A* is an example of a best-first search algorithm. The purpose of A* algorithm is to find a path from one point to another. It’s one of the classics for searching graph algorithms. Let’s figure out how it works using an example. Imagine a 2D game with a top-down view. Let’s divide our game area into square greed, for example 8*8 cells like a chessboard. Our cells can be one of two types, passable or impassable (obstacle). Each period of time a player or an enemy that approaches the player moves one cell. In games, passable cells can be of a different nature, for example, a flat road, grass or sand, which determines the difficulty of moving along them, but for simplicity we’ll assume that all passable cells are passed in the same way. In the picture below, the blue cells are obstacles. Let's assign one cell (or node) as the start cell (the character is in it), and the other cell as the target or goal cell (the one with the flag), and describe how the A* algorithm works for this case. The character is in cell (1,1) and the target is in cell (7,7). Each cell has horizontal, vertical, and diagonal neighbors. It depends on the game, if we calculate diagonal nodes or not. For example in many top-down view games such as Bomberman or Pacman the characters can move only horizontally or vertically. In this case every node, except touching the edges, has only 4 neighbors. If we are talking about a game where characters can move diagonally, every node can have up to 8 neighbors. At the first step of the algorithm, the cell where the character is located has two neighbors. More precisely, three, but one of them is an obstacle. It is clear that the diagonal way is longer. if we set the side of our cell to be conditionally equal to one, then the length of the diagonal of this cell is equal to the square root of two. This is what the Pythagorean theorem says. To get from cell A to cell B, you must first select one of the neighboring cells, and then the next one, and so on. Also, along the way, understand whether it is possible to get from the initial cell to the target one. The A* algorithm at each step selects one of the neighboring cells in accordance with the value of the function F. This function measures how good a candidate cell is to be included in our shortest path. This is the cost function, and it is the sum of the move function G and the heuristic function.

• G cost — is a distance from a starting node.

• H cost (Heuristic) is a distance from the end (goal) node. This function can be different, a developer decides what’s better. Perhaps the choice of H is the most important in A*, and this is the point that makes any particular implementation of the algorithm more or less effective. Theoretically you can use any function you want.

  In our case, we know the position of the target cell and can, for example, calculate geometric Euclidean distance between the target and current cell. The shorter the distance, the closer we are to the goal.

• F cost = G + H. So the algorithm calculates all neighbor nodes F costs and chooses one of the lowest F costs to look at first. When we choose one we mark it as closed and calculate values for this node neighbors.

As we mentioned above, if the characters can move on our grid in 8 directions, then the diagonal step will be longer than the horizontal or vertical one, that is, it will be more expensive. Let us move horizontally, vertically and diagonally. Let's assign the price of “passing” along one cell vertically and horizontally equal, for example, 10, and diagonally — 14, to avoid fractional numbers. This is how our G function will be calculated.

Heuristic functionHow can we calculate H?

This is a heuristic function. The name itself means that it’s determined by experience, and can be different. Here we will take it equal to the so-called Euclidean distance between the points (x1, y1) and (x2, y2): In the picture, for the first step, there are two options, and they are the same in cost, but on the next step, the character gets into a dead end in one of the options. Therefore, we are going the other way. In the next iteration, we already have 4 options. Two of them are not suitable, because they lead backwards, and the other options are equally good, but the algorithm decided that it was best to go diagonally to the cell (3,2). Further, at each step, the calculation of the function F is repeated until the character reaches the target cell. If, of course, such a passage exists. 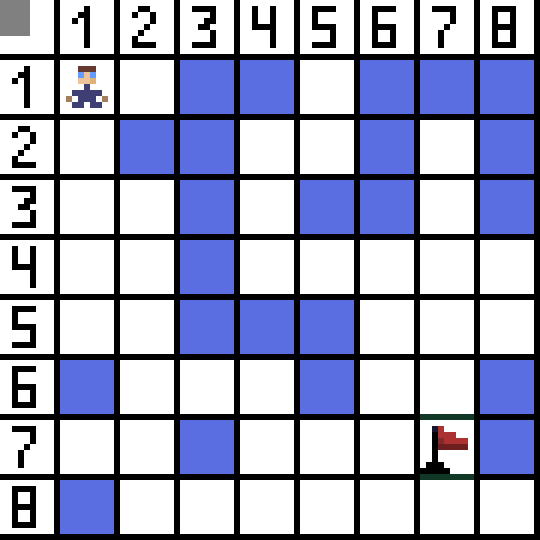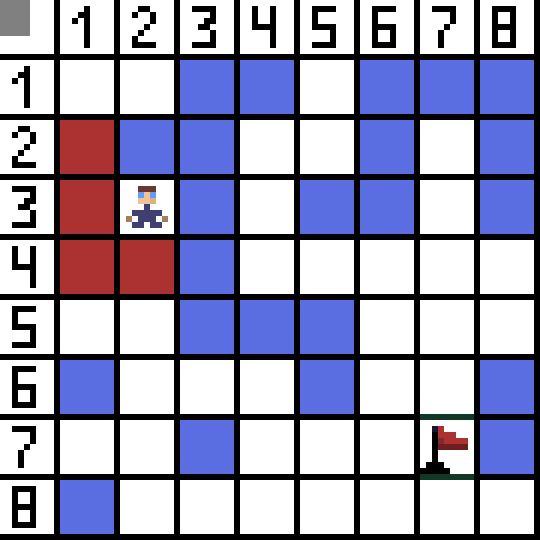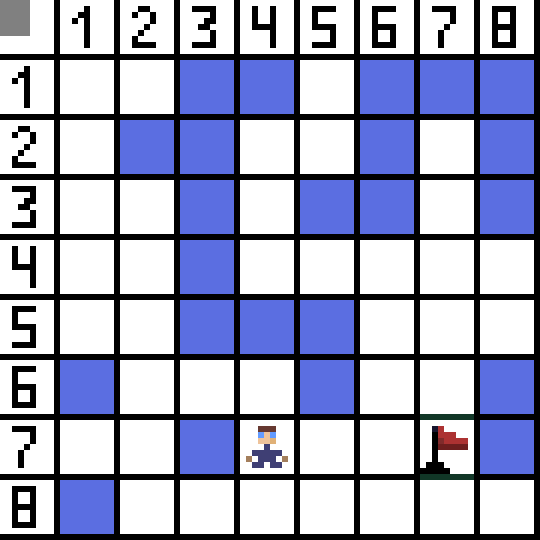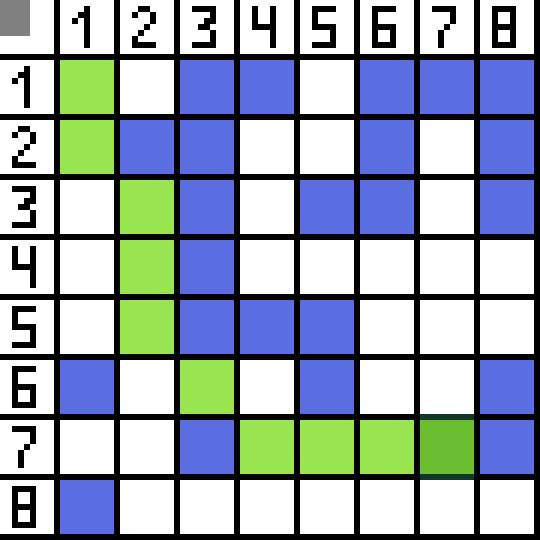Green way on the gif-picture indicates the optimal path of the character to the flag.

A* Algorithm step by step

To implement the algorithm in Java, you need to take the following steps 1. First you need to create two lists, for open nodes and closed nodes. 2. Initialize both lists. In a closed list, the start node points to the open list. 3. while there are elements in the open list: 3a. Find node min with smallest F 3b. Remove min from open list 3c. Determine neighbors min (up to 8, if diagonals are taken into account) 3d. Checking each neighbor: a) if the neighbor is the target cell, stop searching b) If not, calculate G, H for it. G = min.G + distance between neighbor and min F = G + H c) if the node with the same position as the neighbor is in the open list and its F is less than that of the neighbor, skip that neighbor d) if the node with the same position as the neighbor is in the closed list, and its f is less than that of the neighbor, skip that neighbor. Otherwise, add the node to the open list End of inner loop 3e. Adding min to the closed list End of outer loop So, at each iteration we are going to do the next:

• Select the cell from our open list with the lowest estimated total score.
• Remove this cell from the open list.
• Add all the cells that we can reach from it to the open list.
• When we do this, we also process the new score from that node to each new one to see if it's an improvement on what we have so far, and if it is, we update what we know about that cell.

A* Pseudocode

Here is brief pseudocode of A* pathfinding:

Input: a grid with locked and empty cells, with start and goal cell.
Output: least cost path from start to goal cell.

       Initialisation
openList = {startCell} //list of traversed cells
closedList = {}  //list of already traversed cells
g.startCell = 0 //cost from source cell to a cell
h.startCell = h(startCell, goal) //heuristic
f.startCell = g.startCell + h.StartCell

   while openList is not empty
           do

       //let the currentCell equal the cell with the least f value
       currentCell = Cell on top of openList, with least f
      

                if currentCell == end return
       remove currentCell from openList
       add currentCell to closedList
       foreach n in child.currentCell
                    if n in closedList
       continue
       cost = g.currentCell + distance(currentCell,n)
       if (n in openList and cost < g.n)
           remove n from closedList
           g.n = cost
           h.n = h(n, goal)
           f.n = g.n + h.n

From pseudocode to A* Implementation in Java

A* Pathfinding in Java realization should have some methods to serve algorithm:

• Cell, a structure to hold the necessary parameters
• Open and closed lists
• Method to calculate heuristic function
• Method to trace the path from the source to destination
• Methods to check if the given cell is blocked, if it’s already reached, if it’s valid and so on

package Asterist;

import java.util.PriorityQueue;
import java.util.Stack;

public class AAsterisk {

//Java Program to implement A* Search Algorithm

   //Here we're creating a shortcut for (int, int) pair
   public static class Pair {
       int first;
       int second;
       public Pair(int first, int second){
           this.first = first;
           this.second = second;
       }

       @Override
       public boolean equals(Object obj) {
           return obj instanceof Pair && this.first == ((Pair)obj).first && this.second == ((Pair)obj).second;
       }
   }

   // Creating a shortcut for tuple<int, int, int> type
   public static class Details {
       double value;
       int i;
       int j;

       public Details(double value, int i, int j) {
           this.value = value;
           this.i = i;
           this.j = j;
       }
   }

   // a Cell (node) structure
   public static class Cell {
       public Pair parent;
       // f = g + h, where h is heuristic
       public double f, g, h;
       Cell()
       {
           parent = new Pair(-1, -1);
           f = -1;
           g = -1;
           h = -1;
       }

       public Cell(Pair parent, double f, double g, double h) {
           this.parent = parent;
           this.f = f;
           this.g = g;
           this.h = h;
       }
   }

   // method to check if our cell (row, col) is valid
   boolean isValid(int[][] grid, int rows, int cols,
                   Pair point)
   {
       if (rows > 0 && cols > 0)
           return (point.first >= 0) && (point.first < rows)
                   && (point.second >= 0)
                   && (point.second < cols);

       return false;
   }

   //is the cell blocked?

   boolean isUnBlocked(int[][] grid, int rows, int cols,
                       Pair point)
   {
       return isValid(grid, rows, cols, point)
               && grid[point.first][point.second] == 1;
   }

   //Method to check if destination cell has been already reached
   boolean isDestination(Pair position, Pair dest)
   {
       return position == dest || position.equals(dest);
   }

   // Method to calculate heuristic function
   double calculateHValue(Pair src, Pair dest)
   {
       return Math.sqrt(Math.pow((src.first - dest.first), 2.0) + Math.pow((src.second - dest.second), 2.0));
   }

   // Method for tracking the path from source to destination

   void tracePath(
           Cell[][] cellDetails,
           int cols,
           int rows,
           Pair dest)
   {   //A* Search algorithm path
       System.out.println("The Path:  ");

       Stack<Pair> path = new Stack<>();

       int row = dest.first;
       int col = dest.second;

       Pair nextNode = cellDetails[row][col].parent;
       do {
           path.push(new Pair(row, col));
           nextNode = cellDetails[row][col].parent;
           row = nextNode.first;
           col = nextNode.second;
       } while (cellDetails[row][col].parent != nextNode); // until src


       while (!path.empty()) {
           Pair p = path.peek();
           path.pop();
           System.out.println("-> (" + p.first + "," + p.second + ") ");
       }
   }

// A main method, A* Search algorithm to find the shortest path

   void aStarSearch(int[][] grid,
                    int rows,
                    int cols,
                    Pair src,
                    Pair dest)
   {

       if (!isValid(grid, rows, cols, src)) {
           System.out.println("Source is invalid...");
           return;
       }


       if (!isValid(grid, rows, cols, dest)) {
           System.out.println("Destination is invalid...");
           return;
       }


       if (!isUnBlocked(grid, rows, cols, src)
               || !isUnBlocked(grid, rows, cols, dest)) {
           System.out.println("Source or destination is blocked...");
           return;
       }


       if (isDestination(src, dest)) {
           System.out.println("We're already (t)here...");
           return;
       }


       boolean[][] closedList = new boolean[rows][cols];//our closed list

       Cell[][] cellDetails = new Cell[rows][cols];

       int i, j;
       // Initialising of the starting cell
       i = src.first;
       j = src.second;
       cellDetails[i][j] = new Cell();
       cellDetails[i][j].f = 0.0;
       cellDetails[i][j].g = 0.0;
       cellDetails[i][j].h = 0.0;
       cellDetails[i][j].parent = new Pair( i, j );


  // Creating an open list


       PriorityQueue<Details> openList = new PriorityQueue<>((o1, o2) -> (int) Math.round(o1.value - o2.value));

       // Put the starting cell on the open list,   set f.startCell = 0

       openList.add(new Details(0.0, i, j));

       while (!openList.isEmpty()) {
           Details p = openList.peek();
           // Add to the closed list
           i = p.i; // second element of tuple
           j = p.j; // third element of tuple

           // Remove from the open list
           openList.poll();
           closedList[i][j] = true;

              // Generating all the 8 neighbors of the cell

           for (int addX = -1; addX <= 1; addX++) {
               for (int addY = -1; addY <= 1; addY++) {
                   Pair neighbour = new Pair(i + addX, j + addY);
                   if (isValid(grid, rows, cols, neighbour)) {
                       if(cellDetails[neighbour.first] == null){ cellDetails[neighbour.first] = new Cell[cols]; }
                       if (cellDetails[neighbour.first][neighbour.second] == null) {
                           cellDetails[neighbour.first][neighbour.second] = new Cell();
                       }

                       if (isDestination(neighbour, dest)) {
                           cellDetails[neighbour.first][neighbour.second].parent = new Pair ( i, j );
                           System.out.println("The destination cell is found");
                           tracePath(cellDetails, rows, cols, dest);
                           return;
                       }

                       else if (!closedList[neighbour.first][neighbour.second]
                               && isUnBlocked(grid, rows, cols, neighbour)) {
                           double gNew, hNew, fNew;
                           gNew = cellDetails[i][j].g + 1.0;
                           hNew = calculateHValue(neighbour, dest);
                           fNew = gNew + hNew;

                           if (cellDetails[neighbour.first][neighbour.second].f == -1
                                   || cellDetails[neighbour.first][neighbour.second].f > fNew) {

                               openList.add(new Details(fNew, neighbour.first, neighbour.second));

                               // Update the details of this
                               // cell
                               cellDetails[neighbour.first][neighbour.second].g = gNew;
//heuristic function                               cellDetails[neighbour.first][neighbour.second].h = hNew;
                               cellDetails[neighbour.first][neighbour.second].f = fNew;
                               cellDetails[neighbour.first][neighbour.second].parent = new Pair( i, j );
                           }
                       }
                   }
               }
           }
       }

       System.out.println("Failed to find the Destination Cell");
   }

   // test
   public static void main(String[] args) {


   //0: The cell is blocked
  // 1: The cell is not blocked

       int[][] grid = {
               { 1, 1, 0, 0, 1, 0, 0, 0 },
               { 1, 0, 0, 1, 1, 0, 1, 0 },
               { 1, 1, 0, 1, 0, 0, 1, 0 },
               { 1, 1, 0, 1, 1, 1, 1, 1 },
               { 1, 1, 0, 0, 0, 1, 1, 1 },
               { 0, 1, 1, 1, 0, 1, 1, 0 },
               { 1, 1, 0, 1, 1, 1, 1, 0 },
               { 0, 1, 1, 1, 1, 1, 1, 1 }

       };


       // Start is the left-most upper-most corner
       Pair src = new Pair(0,0);
               //(8, 0);

       // Destination is the right-most bottom-most corner
       Pair dest = new Pair(6, 6);

       AAsterisk app = new AAsterisk();
       app.aStarSearch(grid, grid.length , grid[0].length, src, dest);

   }
}

Here in example we've got the same grid as in the picture above. Just "draw" it with a 2D array. The program outputs the following path: It can be seen that this is one of several shortest paths that can be built between these two points. Note that the sixth step in our example in the picture and in the program output is different, although the paths turned out to be equally effective. The program selects one of the many most effective options.

Conclusion

We’ve taking a look at the A* search algorithm, figured out how it works and why it is very good in practice. We have considered only one heuristic function - Euclidean distance. In fact, we can also apply, for example, Manhattan distance, thereby getting rid of the need to calculate the square root. The A* algorithm works great in practice:in video games, finding the shortest path for navigators, building maps.