Verschiedene Suchalgorithmen sind auf unterschiedliche Aufgaben zugeschnitten. Heute sprechen wir über die A*-Suche, einen der effektivsten Pfadfindungsalgorithmen. Dieses eignet sich sehr gut für Computerspiele und zum Erstellen von Suchdiagrammen, z. B. für Wege zwischen Städten usw. Möglicherweise haben Sie beispielsweise bei strategischen oder taktischen Videospielen bemerkt, dass Ihr Spieler oder Ihre Gruppe nach dem Drücken einer Taste sofort und ohne Verzögerung beginnt, über das Spielfeld zu dem von Ihnen angegebenen Punkt zu gehen. Es gibt keine Verzögerung, gerade weil die Spiele effektive Algorithmen verwenden, die genau berechnen, wie der Spieler irgendwohin gelangen muss. Oder ein Feind, der den Spieler unverkennbar findet und aus der Ferne in die richtige Richtung läuft. Normalerweise wird für solche Aktionen der A*-Algorithmus verwendet.
Was ist ein A*-Algorithmus?
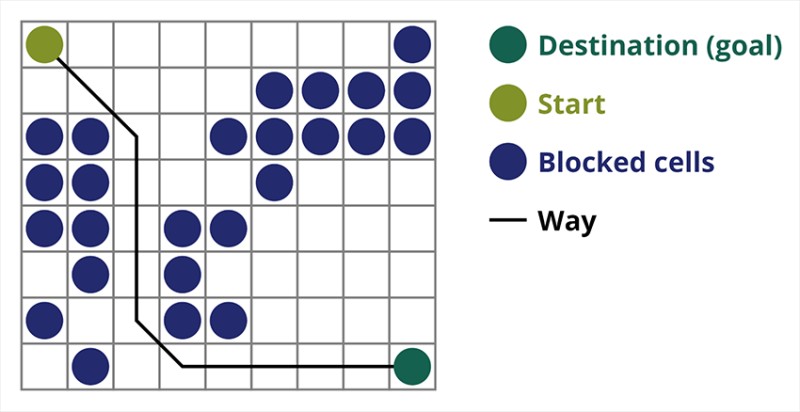
Der Pfadfindungsalgorithmus A* ist ein Beispiel für einen Best-First-Suchalgorithmus. Der Zweck des A*-Algorithmus besteht darin, einen Pfad von einem Punkt zum anderen zu finden. Es ist einer der Klassiker für die Suche nach Graphalgorithmen. Lassen Sie uns anhand eines Beispiels herausfinden, wie es funktioniert. Stellen Sie sich ein 2D-Spiel mit einer Draufsicht vor. Teilen wir unseren Spielbereich in Quadrate auf, zum Beispiel 8*8 Zellen wie ein Schachbrett. Es gibt zwei Arten unserer Zellen: passierbar oder unpassierbar (Hindernis). Jedes Mal bewegt sich ein Spieler oder ein Feind, der sich dem Spieler nähert, ein Feld. In Spielen können passierbare Felder unterschiedlicher Natur sein, zum Beispiel eine ebene Straße, Gras oder Sand, was die Schwierigkeit bestimmt, sich auf ihnen fortzubewegen. Der Einfachheit halber gehen wir jedoch davon aus, dass alle passierbaren Felder auf die gleiche Weise passiert werden. Im Bild unten sind die blauen Zellen Hindernisse.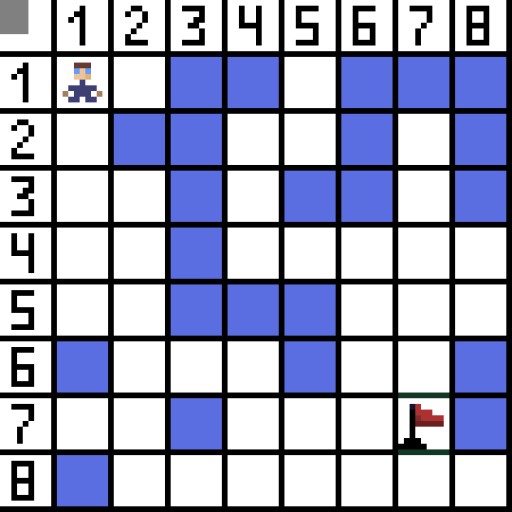
Lassen Sie uns eine Zelle (oder einen Knoten) als Startzelle (das Zeichen befindet sich darin) und die andere Zelle als Ziel- oder Zielzelle (die mit der Flagge) zuweisen und beschreiben, wie der A*-Algorithmus in diesem Fall funktioniert. Der Charakter befindet sich in Zelle (1,1) und das Ziel befindet sich in Zelle (7,7). Jede Zelle hat horizontale, vertikale und diagonale Nachbarn. Es hängt vom Spiel ab, ob wir Diagonalknoten berechnen oder nicht. Beispielsweise können sich die Charaktere in vielen Top-Down-View-Spielen wie Bomberman oder Pacman nur horizontal oder vertikal bewegen. In diesem Fall hat jeder Knoten, mit Ausnahme der Kanten, die ihn berühren, nur 4 Nachbarn. Wenn es sich um ein Spiel handelt, bei dem sich Charaktere diagonal bewegen können, kann jeder Knoten bis zu 8 Nachbarn haben. Im ersten Schritt des Algorithmus hat die Zelle, in der sich das Zeichen befindet, zwei Nachbarn. Genauer gesagt drei, aber einer davon ist ein Hindernis. 
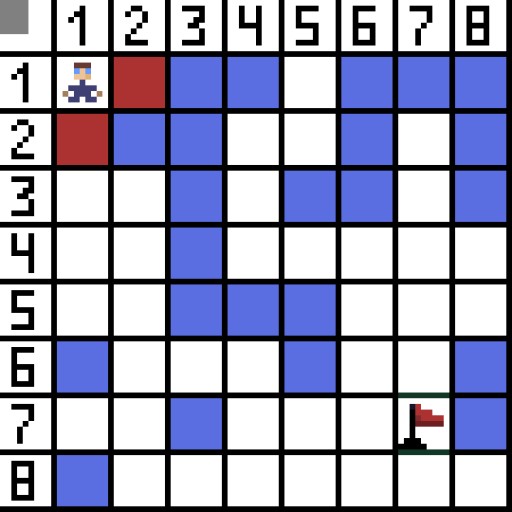Es ist klar, dass der diagonale Weg länger ist. Wenn wir die Seite unserer Zelle bedingt gleich eins setzen, dann ist die Länge der Diagonale dieser Zelle gleich der Quadratwurzel von zwei. Das sagt der Satz des Pythagoras. Um von Zelle A zu Zelle B zu gelangen, müssen Sie zuerst eine der benachbarten Zellen auswählen, dann die nächste und so weiter. Verstehen Sie nebenbei auch, ob es möglich ist, von der Ausgangszelle zur Zielzelle zu gelangen. Der A*-Algorithmus wählt bei jedem Schritt eine der benachbarten Zellen entsprechend dem Wert der Funktion F aus. Diese Funktion misst, wie gut eine Kandidatenzelle in unseren kürzesten Weg aufgenommen werden kann. Dies ist die Kostenfunktion und die Summe der Bewegungsfunktion G und der heuristischen Funktion.
-
G-Kosten – ist eine Entfernung von einem Startknoten.
-
H-Kosten (heuristisch) sind die Entfernung vom Endknoten (Zielknoten). Diese Funktion kann unterschiedlich sein, ein Entwickler entscheidet, was besser ist. Vielleicht ist die Wahl von H die wichtigste in A*, und das ist der Punkt, der jede bestimmte Implementierung des Algorithmus mehr oder weniger effektiv macht. Theoretisch können Sie jede gewünschte Funktion verwenden.
In unserem Fall kennen wir die Position der Zielzelle und können beispielsweise den geometrischen euklidischen Abstand zwischen Ziel und aktueller Zelle berechnen. Je kürzer die Distanz, desto näher sind wir dem Ziel.
-
F-Kosten = G + H. Der Algorithmus berechnet also die F-Kosten aller Nachbarknoten und wählt einen der niedrigsten F-Kosten aus, der zuerst betrachtet wird. Wenn wir einen auswählen, markieren wir ihn als geschlossen und berechnen die Werte für die Nachbarn dieses Knotens.
Heuristische FunktionWie können wir H berechnen?
Dies ist eine heuristische Funktion. Der Name selbst bedeutet, dass er durch Erfahrung bestimmt wird und unterschiedlich sein kann. Hier nehmen wir es gleich dem sogenannten euklidischen Abstand zwischen den Punkten (x1, y1) und (x2, y2):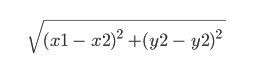
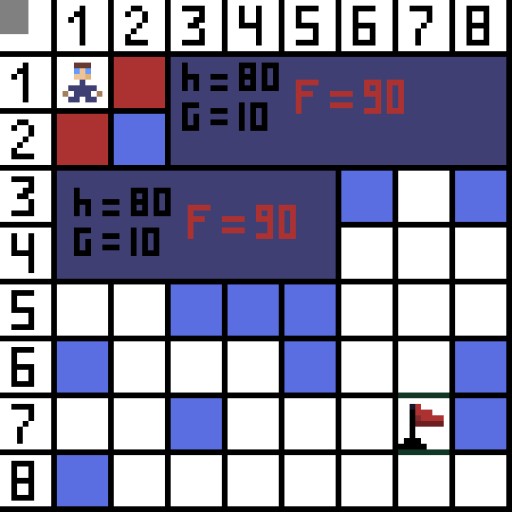Im Bild gibt es für den ersten Schritt zwei Optionen, und sie kosten gleich viel: Doch im nächsten Schritt gerät der Charakter bei einer der Optionen in eine Sackgasse. Deshalb gehen wir den anderen Weg. In der nächsten Iteration haben wir bereits 4 Optionen. 
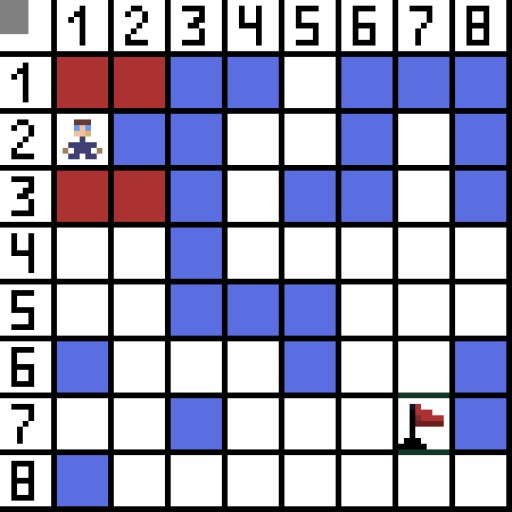Zwei davon sind nicht geeignet, weil sie nach hinten führen, und die anderen Optionen sind genauso gut, aber der Algorithmus hat entschieden, dass es am besten ist, diagonal zur Zelle (3,2) zu gehen. Darüber hinaus wird bei jedem Schritt die Berechnung der Funktion F wiederholt, bis das Zeichen die Zielzelle erreicht. Wenn es natürlich eine solche Passage gibt. 
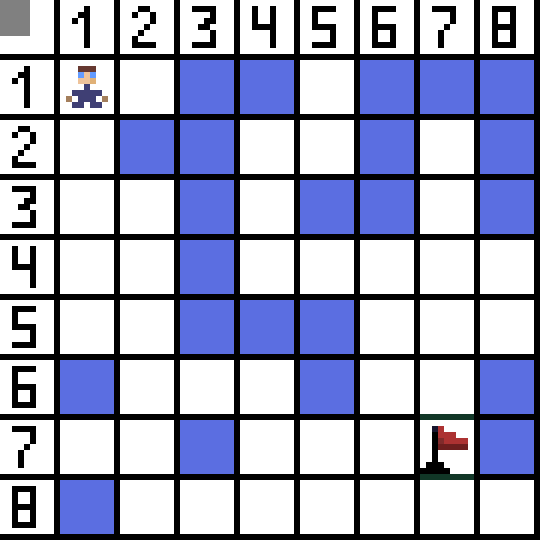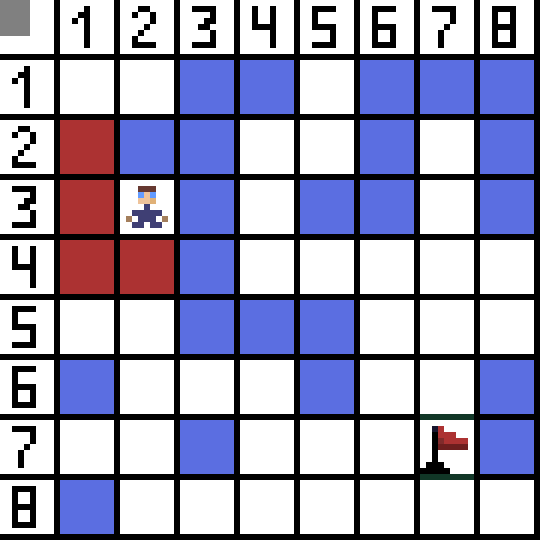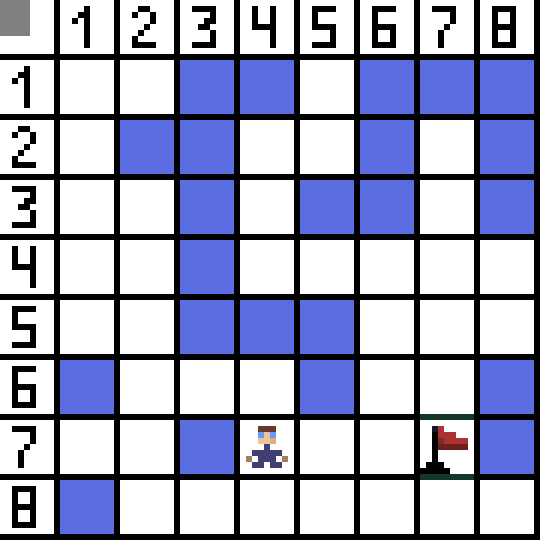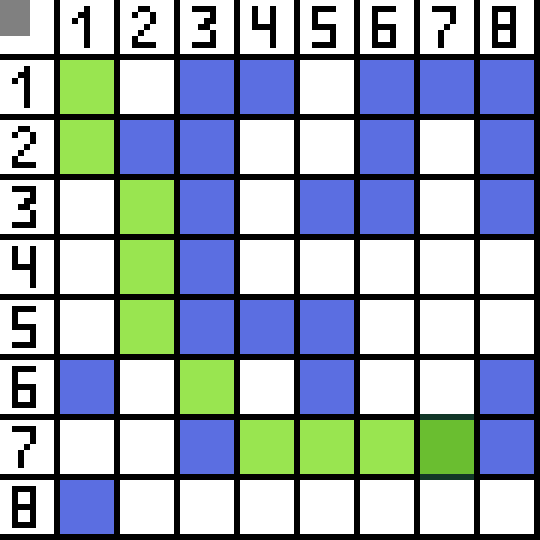Der grüne Weg auf dem GIF-Bild zeigt den optimalen Weg des Charakters zur Flagge an.
A* Algorithmus Schritt für Schritt
Um den Algorithmus in Java zu implementieren, müssen Sie die folgenden Schritte ausführen: 1. Zuerst müssen Sie zwei Listen erstellen, für offene Knoten und geschlossene Knoten. 2. Initialisieren Sie beide Listen. In einer geschlossenen Liste zeigt der Startknoten auf die offene Liste. 3. solange Elemente in der offenen Liste vorhanden sind: 3a. Finden Sie den Knoten min mit dem kleinsten F 3b. Entfernen Sie min aus der offenen Liste 3c. Bestimmen Sie die Mindestanzahl der Nachbarn (bis zu 8, wenn Diagonalen berücksichtigt werden) 3d. Überprüfen Sie jeden Nachbarn: a) Wenn der Nachbar die Zielzelle ist, beenden Sie die Suche. b) Wenn nicht, berechnen Sie G, H dafür. G = min.G + Abstand zwischen Nachbar und min F = G + H c) wenn der Knoten mit der gleichen Position wie der Nachbar in der offenen Liste ist und sein F kleiner als der des Nachbarn ist, überspringe diesen Nachbarn d) wenn Der Knoten mit derselben Position wie der Nachbar befindet sich in der geschlossenen Liste und sein f ist kleiner als das des Nachbarn. Überspringen Sie diesen Nachbarn. Andernfalls fügen Sie den Knoten zur offenen Liste hinzu. Ende der inneren Schleife 3e. Hinzufügen von „min“ zur geschlossenen Liste. Ende der äußeren Schleife. Bei jeder Iteration werden wir also Folgendes tun:- Wählen Sie aus unserer offenen Liste die Zelle mit der niedrigsten geschätzten Gesamtpunktzahl aus.
- Entfernen Sie diese Zelle aus der geöffneten Liste.
- Fügen Sie alle Zellen, die wir von dort aus erreichen können, zur offenen Liste hinzu.
- Wenn wir dies tun, verarbeiten wir auch die neue Bewertung von diesem Knoten zu jedem neuen, um zu sehen, ob es sich um eine Verbesserung gegenüber dem, was wir bisher haben, handelt, und wenn ja, aktualisieren wir, was wir über diese Zelle wissen.
A* Pseudocode
Hier ist ein kurzer Pseudocode der A*-Pfadfindung:Input: a grid with locked and empty cells, with start and goal cell.
Output: least cost path from start to goal cell.
Initialisation
openList = {startCell} //list of traversed cells
closedList = {} //list of already traversed cells
g.startCell = 0 //cost from source cell to a cell
h.startCell = h(startCell, goal) //heuristic
f.startCell = g.startCell + h.StartCell
while openList is not empty
do
//let the currentCell equal the cell with the least f value
currentCell = Cell on top of openList, with least f
if currentCell == end return
remove currentCell from openList
add currentCell to closedList
foreach n in child.currentCell
if n in closedList
continue
cost = g.currentCell + distance(currentCell,n)
if (n in openList and cost < g.n)
remove n from closedList
g.n = cost
h.n = h(n, goal)
f.n = g.n + h.nVom Pseudocode zur A*-Implementierung in Java
Eine * Pathfinding in Java-Realisierung sollte über einige Methoden verfügen, um den Algorithmus zu bedienen:- Zelle, eine Struktur zum Speichern der erforderlichen Parameter
- Offene und geschlossene Listen
- Methode zur Berechnung einer heuristischen Funktion
- Methode zum Verfolgen des Pfads von der Quelle zum Ziel
- Methoden zum Überprüfen, ob die angegebene Zelle blockiert ist, ob sie bereits erreicht ist, ob sie gültig ist usw
package Asterist;
import java.util.PriorityQueue;
import java.util.Stack;
public class AAsterisk {
//Java Program to implement A* Search Algorithm
//Here we're creating a shortcut for (int, int) pair
public static class Pair {
int first;
int second;
public Pair(int first, int second){
this.first = first;
this.second = second;
}
@Override
public boolean equals(Object obj) {
return obj instanceof Pair && this.first == ((Pair)obj).first && this.second == ((Pair)obj).second;
}
}
// Creating a shortcut for tuple<int, int, int> type
public static class Details {
double value;
int i;
int j;
public Details(double value, int i, int j) {
this.value = value;
this.i = i;
this.j = j;
}
}
// a Cell (node) structure
public static class Cell {
public Pair parent;
// f = g + h, where h is heuristic
public double f, g, h;
Cell()
{
parent = new Pair(-1, -1);
f = -1;
g = -1;
h = -1;
}
public Cell(Pair parent, double f, double g, double h) {
this.parent = parent;
this.f = f;
this.g = g;
this.h = h;
}
}
// method to check if our cell (row, col) is valid
boolean isValid(int[][] grid, int rows, int cols,
Pair point)
{
if (rows > 0 && cols > 0)
return (point.first >= 0) && (point.first < rows)
&& (point.second >= 0)
&& (point.second < cols);
return false;
}
//is the cell blocked?
boolean isUnBlocked(int[][] grid, int rows, int cols,
Pair point)
{
return isValid(grid, rows, cols, point)
&& grid[point.first][point.second] == 1;
}
//Method to check if destination cell has been already reached
boolean isDestination(Pair position, Pair dest)
{
return position == dest || position.equals(dest);
}
// Method to calculate heuristic function
double calculateHValue(Pair src, Pair dest)
{
return Math.sqrt(Math.pow((src.first - dest.first), 2.0) + Math.pow((src.second - dest.second), 2.0));
}
// Method for tracking the path from source to destination
void tracePath(
Cell[][] cellDetails,
int cols,
int rows,
Pair dest)
{ //A* Search algorithm path
System.out.println("The Path: ");
Stack<Pair> path = new Stack<>();
int row = dest.first;
int col = dest.second;
Pair nextNode = cellDetails[row][col].parent;
do {
path.push(new Pair(row, col));
nextNode = cellDetails[row][col].parent;
row = nextNode.first;
col = nextNode.second;
} while (cellDetails[row][col].parent != nextNode); // until src
while (!path.empty()) {
Pair p = path.peek();
path.pop();
System.out.println("-> (" + p.first + "," + p.second + ") ");
}
}
// A main method, A* Search algorithm to find the shortest path
void aStarSearch(int[][] grid,
int rows,
int cols,
Pair src,
Pair dest)
{
if (!isValid(grid, rows, cols, src)) {
System.out.println("Source is invalid...");
return;
}
if (!isValid(grid, rows, cols, dest)) {
System.out.println("Destination is invalid...");
return;
}
if (!isUnBlocked(grid, rows, cols, src)
|| !isUnBlocked(grid, rows, cols, dest)) {
System.out.println("Source or destination is blocked...");
return;
}
if (isDestination(src, dest)) {
System.out.println("We're already (t)here...");
return;
}
boolean[][] closedList = new boolean[rows][cols];//our closed list
Cell[][] cellDetails = new Cell[rows][cols];
int i, j;
// Initialising of the starting cell
i = src.first;
j = src.second;
cellDetails[i][j] = new Cell();
cellDetails[i][j].f = 0.0;
cellDetails[i][j].g = 0.0;
cellDetails[i][j].h = 0.0;
cellDetails[i][j].parent = new Pair( i, j );
// Creating an open list
PriorityQueue<Details> openList = new PriorityQueue<>((o1, o2) -> (int) Math.round(o1.value - o2.value));
// Put the starting cell on the open list, set f.startCell = 0
openList.add(new Details(0.0, i, j));
while (!openList.isEmpty()) {
Details p = openList.peek();
// Add to the closed list
i = p.i; // second element of tuple
j = p.j; // third element of tuple
// Remove from the open list
openList.poll();
closedList[i][j] = true;
// Generating all the 8 neighbors of the cell
for (int addX = -1; addX <= 1; addX++) {
for (int addY = -1; addY <= 1; addY++) {
Pair neighbour = new Pair(i + addX, j + addY);
if (isValid(grid, rows, cols, neighbour)) {
if(cellDetails[neighbour.first] == null){ cellDetails[neighbour.first] = new Cell[cols]; }
if (cellDetails[neighbour.first][neighbour.second] == null) {
cellDetails[neighbour.first][neighbour.second] = new Cell();
}
if (isDestination(neighbour, dest)) {
cellDetails[neighbour.first][neighbour.second].parent = new Pair ( i, j );
System.out.println("The destination cell is found");
tracePath(cellDetails, rows, cols, dest);
return;
}
else if (!closedList[neighbour.first][neighbour.second]
&& isUnBlocked(grid, rows, cols, neighbour)) {
double gNew, hNew, fNew;
gNew = cellDetails[i][j].g + 1.0;
hNew = calculateHValue(neighbour, dest);
fNew = gNew + hNew;
if (cellDetails[neighbour.first][neighbour.second].f == -1
|| cellDetails[neighbour.first][neighbour.second].f > fNew) {
openList.add(new Details(fNew, neighbour.first, neighbour.second));
// Update the details of this
// cell
cellDetails[neighbour.first][neighbour.second].g = gNew;
//heuristic function cellDetails[neighbour.first][neighbour.second].h = hNew;
cellDetails[neighbour.first][neighbour.second].f = fNew;
cellDetails[neighbour.first][neighbour.second].parent = new Pair( i, j );
}
}
}
}
}
}
System.out.println("Failed to find the Destination Cell");
}
// test
public static void main(String[] args) {
//0: The cell is blocked
// 1: The cell is not blocked
int[][] grid = {
{ 1, 1, 0, 0, 1, 0, 0, 0 },
{ 1, 0, 0, 1, 1, 0, 1, 0 },
{ 1, 1, 0, 1, 0, 0, 1, 0 },
{ 1, 1, 0, 1, 1, 1, 1, 1 },
{ 1, 1, 0, 0, 0, 1, 1, 1 },
{ 0, 1, 1, 1, 0, 1, 1, 0 },
{ 1, 1, 0, 1, 1, 1, 1, 0 },
{ 0, 1, 1, 1, 1, 1, 1, 1 }
};
// Start is the left-most upper-most corner
Pair src = new Pair(0,0);
//(8, 0);
// Destination is the right-most bottom-most corner
Pair dest = new Pair(6, 6);
AAsterisk app = new AAsterisk();
app.aStarSearch(grid, grid.length , grid[0].length, src, dest);
}
}
Der Pfad: -> (0,0) -> (1,0) -> (2,1) -> (3,1) -> (4,1) -> (5,2) -> (5, 3) -> (6,4) -> (6,5) -> (6,6)
Es ist ersichtlich, dass dies einer von mehreren kürzesten Wegen ist, die zwischen diesen beiden Punkten gebaut werden können. Beachten Sie, dass der sechste Schritt in unserem Beispiel im Bild und in der Programmausgabe unterschiedlich ist, obwohl sich die Pfade als gleich effektiv erwiesen haben. Das Programm wählt eine der effektivsten Optionen aus.
GO TO FULL VERSION