Ang iba't ibang mga algorithm sa paghahanap ay iniangkop para sa iba't ibang mga gawain. Ngayon ay pag-uusapan natin ang tungkol sa A* search, isa sa pinakaepektibong pathfinding algorithm. Ang isang ito ay napakahusay na angkop para sa mga laro sa computer at pagbuo ng mga search graph tulad ng mga paraan sa pagitan ng mga lungsod at iba pa. Maaaring napansin mo, halimbawa, sa mga madiskarteng o taktikal na video game, kung paano pagkatapos ng pagpindot sa isang pindutan, ang iyong manlalaro o grupo ay magsisimula kaagad nang walang pagkaantala upang pumunta sa kabila ng field hanggang sa puntong iyong tinukoy. Walang tiyak na pagkaantala dahil ang mga laro ay gumagamit ng mga epektibong algorithm na eksaktong kinakalkula kung paano kailangang makarating ang manlalaro sa isang lugar. O isang kaaway na hindi mapag-aalinlanganan na nahahanap ang manlalaro at nagsimulang maglakad sa tamang direksyon mula sa malayo. Karaniwan, ang A* algorithm ay ginagamit para sa mga naturang aksyon.
Ano ang A* algorithm
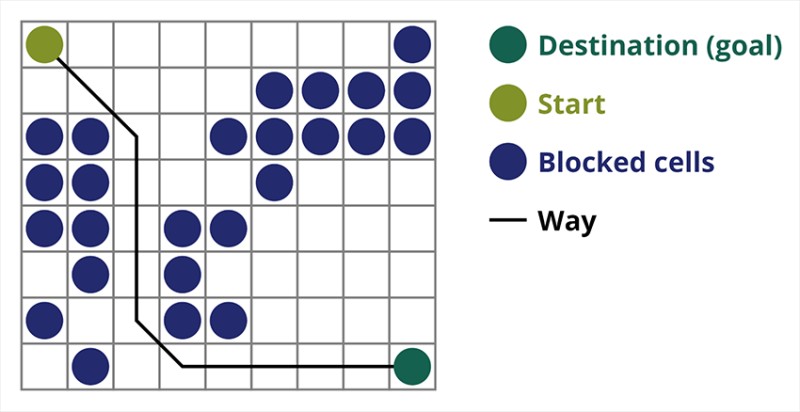
Ang Pathfinding algorithm A* ay isang halimbawa ng isang pinakamahusay na unang algorithm sa paghahanap. Ang layunin ng A* algorithm ay maghanap ng landas mula sa isang punto patungo sa isa pa. Isa ito sa mga classic para sa paghahanap ng mga graph algorithm. Alamin natin kung paano ito gumagana gamit ang isang halimbawa. Isipin ang isang 2D na laro na may top-down na view. Hatiin natin ang lugar ng laro natin sa square greed, halimbawa 8*8 cells na parang chessboard. Ang ating mga cell ay maaaring isa sa dalawang uri, passable o hindi madaanan (bstacle). Bawat yugto ng panahon ang isang manlalaro o isang kaaway na lumalapit sa manlalaro ay gumagalaw ng isang cell. Sa mga laro, ang mga passable cell ay maaaring may ibang kalikasan, halimbawa, isang patag na kalsada, damo o buhangin, na tumutukoy sa kahirapan ng paglipat sa kanila, ngunit para sa pagiging simple, ipagpalagay natin na ang lahat ng mga passable na cell ay ipinapasa sa parehong paraan. Sa larawan sa ibaba, ang mga asul na selula ay mga hadlang.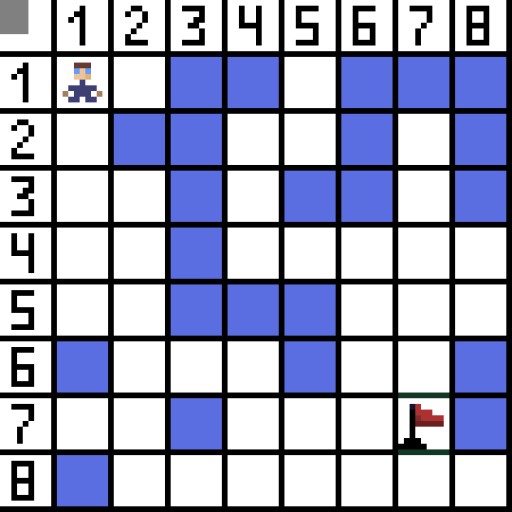
Magtalaga tayo ng isang cell (o node) bilang panimulang cell (nasa loob nito ang character), at ang isa pang cell bilang target o cell ng layunin (ang may flag), at ilarawan kung paano gumagana ang A* algorithm para sa kasong ito. Ang karakter ay nasa cell (1,1) at ang target ay nasa cell (7,7). Ang bawat cell ay may pahalang, patayo, at dayagonal na mga kapitbahay. Depende ito sa laro, kung kalkulahin natin ang mga diagonal node o hindi. Halimbawa sa maraming top-down view na laro tulad ng Bomberman o Pacman ang mga character ay maaari lamang gumalaw nang pahalang o patayo. Sa kasong ito, ang bawat node, maliban sa pagpindot sa mga gilid, ay mayroon lamang 4 na kapitbahay. Kung pinag-uusapan natin ang tungkol sa isang laro kung saan ang mga character ay maaaring gumalaw nang pahilis, ang bawat node ay maaaring magkaroon ng hanggang 8 kapitbahay. Sa unang hakbang ng algorithm, ang cell kung saan matatagpuan ang character ay may dalawang kapitbahay. Mas tiyak, tatlo, ngunit ang isa sa kanila ay isang balakid. 
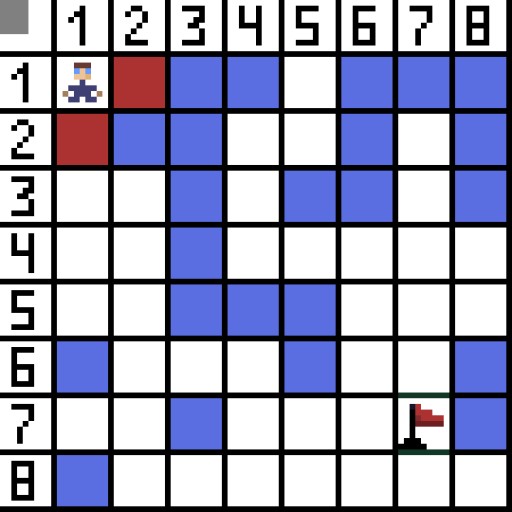Ito ay malinaw na ang dayagonal na paraan ay mas mahaba. kung itinakda namin ang gilid ng aming cell na may kondisyon na katumbas ng isa, kung gayon ang haba ng dayagonal ng cell na ito ay katumbas ng square root ng dalawa. Ito ang sinasabi ng Pythagorean theorem. Upang makakuha mula sa cell A patungo sa cell B, kailangan mo munang pumili ng isa sa mga kalapit na cell, at pagkatapos ay ang susunod, at iba pa. Gayundin, sa daan, unawain kung posible bang makarating mula sa unang cell patungo sa target. Ang A* algorithm sa bawat hakbang ay pumipili ng isa sa mga kalapit na cell alinsunod sa halaga ng function na F. Sinusukat ng function na ito kung gaano kahusay ang isang kandidatong cell na maisama sa aming pinakamaikling landas. Ito ang function ng gastos, at ito ang kabuuan ng function ng paglipat G at ang heuristic function.
-
G cost — ay isang distansya mula sa isang panimulang node.
-
Ang H cost (Heuristic) ay isang distansya mula sa dulo (goal) node. Maaaring iba ang function na ito, ang isang developer ang magpapasya kung ano ang mas mahusay. Marahil ang pagpili ng H ay ang pinakamahalaga sa A*, at ito ang punto na ginagawang mas o hindi gaanong epektibo ang anumang partikular na pagpapatupad ng algorithm. Sa teoryang maaari mong gamitin ang anumang function na gusto mo.
Sa aming kaso, alam namin ang posisyon ng target na cell at maaari, halimbawa, kalkulahin ang geometric na Euclidean na distansya sa pagitan ng target at kasalukuyang cell. Kung mas maikli ang distansya, mas malapit tayo sa layunin.
-
F cost = G + H. Kaya kinakalkula ng algorithm ang lahat ng mga kapitbahay na node na halaga ng F at pinipili ang isa sa pinakamababang halaga ng F na titingnan muna. Kapag pumili kami ng isa ay minarkahan namin ito bilang sarado at kinakalkula ang mga halaga para sa mga kapitbahay ng node na ito.
Heuristic functionPaano natin makalkula ang H?
Ito ay isang heuristic function. Ang pangalan mismo ay nangangahulugan na ito ay tinutukoy ng karanasan, at maaaring iba. Dito ay kukunin natin itong katumbas ng tinatawag na Euclidean na distansya sa pagitan ng mga puntos (x1, y1) at (x2, y2):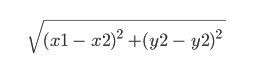
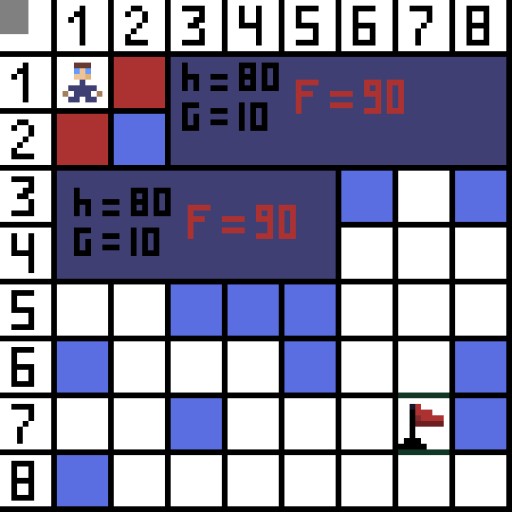Sa larawan, para sa unang hakbang, mayroong dalawang pagpipilian, at pareho sila sa gastos, ngunit sa susunod na hakbang, ang karakter ay napupunta sa isang dead end sa isa sa mga opsyon. Samakatuwid, kami ay pupunta sa ibang paraan. Sa susunod na pag-ulit, mayroon na tayong 4 na opsyon. 
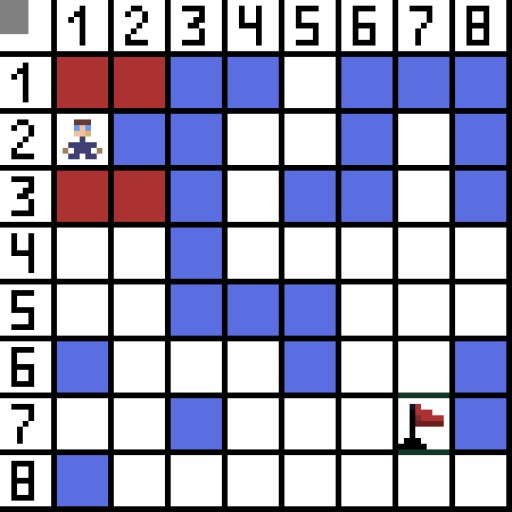Dalawa sa kanila ay hindi angkop, dahil humahantong sila pabalik, at ang iba pang mga pagpipilian ay pantay na mabuti, ngunit ang algorithm ay nagpasya na ito ay pinakamahusay na pumunta sa pahilis sa cell (3,2). Dagdag pa, sa bawat hakbang, ang pagkalkula ng function F ay paulit-ulit hanggang sa maabot ng character ang target na cell. Kung, siyempre, umiiral ang gayong sipi. 
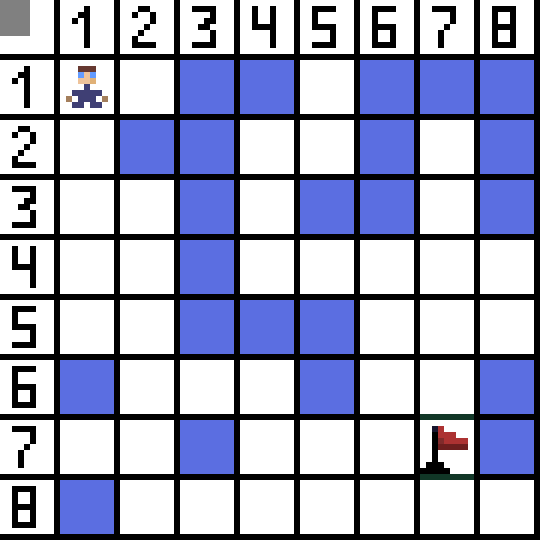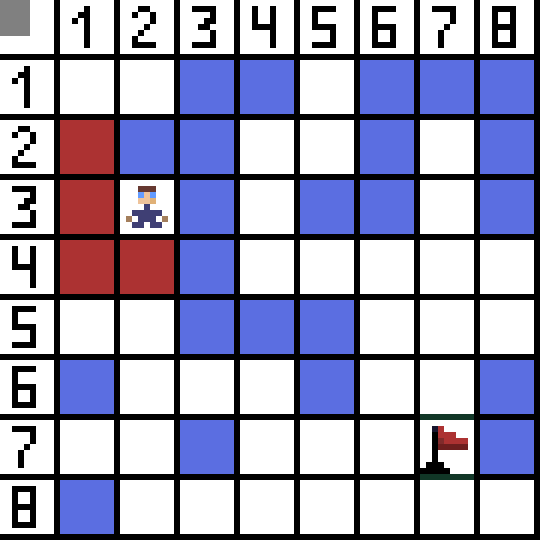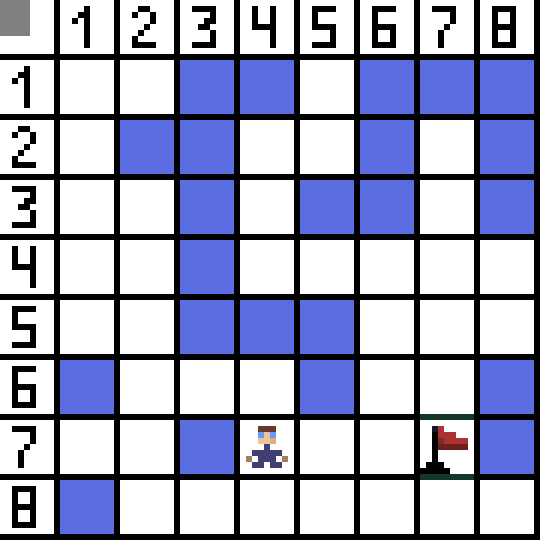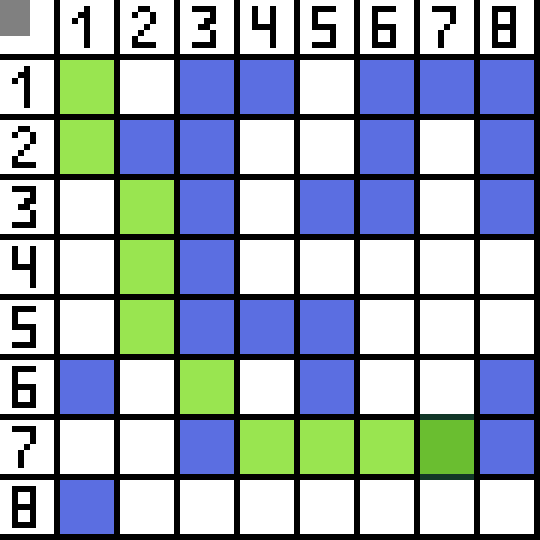Ang berdeng paraan sa gif-picture ay nagpapahiwatig ng pinakamainam na landas ng character patungo sa bandila.
A* Algorithm hakbang-hakbang
Upang ipatupad ang algorithm sa Java, kailangan mong gawin ang mga sumusunod na hakbang 1. Una kailangan mong lumikha ng dalawang listahan, para sa mga bukas na node at sarado na mga node. 2. Simulan ang parehong mga listahan. Sa isang saradong listahan, ang panimulang node ay tumuturo sa bukas na listahan. 3. habang may mga elemento sa bukas na listahan: 3a. Maghanap ng node min na may pinakamaliit na F 3b. Alisin ang min mula sa bukas na listahan 3c. Tukuyin ang mga kapitbahay min (hanggang 8, kung ang mga diagonal ay isinasaalang-alang) 3d. Sinusuri ang bawat kapitbahay: a) kung ang kapitbahay ay ang target na cell, itigil ang paghahanap b) Kung hindi, kalkulahin ang G, H para dito. G = min.G + distansya sa pagitan ng kapitbahay at min F = G + H c) kung ang node na may parehong posisyon sa kapitbahay ay nasa bukas na listahan at ang F nito ay mas mababa kaysa sa kapitbahay, laktawan ang kapitbahay na iyon d) kung ang node na may parehong posisyon sa kapitbahay ay nasa saradong listahan, at ang f nito ay mas mababa kaysa sa kapitbahay, laktawan ang kapitbahay na iyon. Kung hindi, idagdag ang node sa bukas na listahan End of inner loop 3e. Pagdaragdag ng min sa saradong listahan Katapusan ng panlabas na loop Kaya, sa bawat pag-ulit ay gagawin natin ang susunod:- Piliin ang cell mula sa aming bukas na listahan na may pinakamababang tinantyang kabuuang marka.
- Alisin ang cell na ito mula sa bukas na listahan.
- Idagdag ang lahat ng mga cell na maaari naming maabot mula dito sa bukas na listahan.
- Kapag ginawa namin ito, pinoproseso din namin ang bagong marka mula sa node na iyon patungo sa bawat bago upang makita kung ito ay isang pagpapabuti sa kung ano ang mayroon kami sa ngayon, at kung ito ay, ina-update namin ang alam namin tungkol sa cell na iyon.
A* Pseudocode
Narito ang maikling pseudocode ng A* pathfinding:Input: a grid with locked and empty cells, with start and goal cell.
Output: least cost path from start to goal cell.
Initialisation
openList = {startCell} //list of traversed cells
closedList = {} //list of already traversed cells
g.startCell = 0 //cost from source cell to a cell
h.startCell = h(startCell, goal) //heuristic
f.startCell = g.startCell + h.StartCell
while openList is not empty
do
//let the currentCell equal the cell with the least f value
currentCell = Cell on top of openList, with least f
if currentCell == end return
remove currentCell from openList
add currentCell to closedList
foreach n in child.currentCell
if n in closedList
continue
cost = g.currentCell + distance(currentCell,n)
if (n in openList and cost < g.n)
remove n from closedList
g.n = cost
h.n = h(n, goal)
f.n = g.n + h.nMula sa pseudocode hanggang A* Pagpapatupad sa Java
Ang A* Pathfinding sa Java realization ay dapat magkaroon ng ilang mga pamamaraan upang maghatid ng algorithm:- Cell, isang istraktura upang hawakan ang mga kinakailangang parameter
- Buksan at isinara ang mga listahan
- Paraan ng pagkalkula ng heuristic function
- Paraan upang masubaybayan ang landas mula sa pinagmulan hanggang sa patutunguhan
- Mga pamamaraan upang suriin kung ang ibinigay na cell ay naka-block, kung naabot na ito, kung ito ay wasto at iba pa
package Asterist;
import java.util.PriorityQueue;
import java.util.Stack;
public class AAsterisk {
//Java Program to implement A* Search Algorithm
//Here we're creating a shortcut for (int, int) pair
public static class Pair {
int first;
int second;
public Pair(int first, int second){
this.first = first;
this.second = second;
}
@Override
public boolean equals(Object obj) {
return obj instanceof Pair && this.first == ((Pair)obj).first && this.second == ((Pair)obj).second;
}
}
// Creating a shortcut for tuple<int, int, int> type
public static class Details {
double value;
int i;
int j;
public Details(double value, int i, int j) {
this.value = value;
this.i = i;
this.j = j;
}
}
// a Cell (node) structure
public static class Cell {
public Pair parent;
// f = g + h, where h is heuristic
public double f, g, h;
Cell()
{
parent = new Pair(-1, -1);
f = -1;
g = -1;
h = -1;
}
public Cell(Pair parent, double f, double g, double h) {
this.parent = parent;
this.f = f;
this.g = g;
this.h = h;
}
}
// method to check if our cell (row, col) is valid
boolean isValid(int[][] grid, int rows, int cols,
Pair point)
{
if (rows > 0 && cols > 0)
return (point.first >= 0) && (point.first < rows)
&& (point.second >= 0)
&& (point.second < cols);
return false;
}
//is the cell blocked?
boolean isUnBlocked(int[][] grid, int rows, int cols,
Pair point)
{
return isValid(grid, rows, cols, point)
&& grid[point.first][point.second] == 1;
}
//Method to check if destination cell has been already reached
boolean isDestination(Pair position, Pair dest)
{
return position == dest || position.equals(dest);
}
// Method to calculate heuristic function
double calculateHValue(Pair src, Pair dest)
{
return Math.sqrt(Math.pow((src.first - dest.first), 2.0) + Math.pow((src.second - dest.second), 2.0));
}
// Method for tracking the path from source to destination
void tracePath(
Cell[][] cellDetails,
int cols,
int rows,
Pair dest)
{ //A* Search algorithm path
System.out.println("The Path: ");
Stack<Pair> path = new Stack<>();
int row = dest.first;
int col = dest.second;
Pair nextNode = cellDetails[row][col].parent;
do {
path.push(new Pair(row, col));
nextNode = cellDetails[row][col].parent;
row = nextNode.first;
col = nextNode.second;
} while (cellDetails[row][col].parent != nextNode); // until src
while (!path.empty()) {
Pair p = path.peek();
path.pop();
System.out.println("-> (" + p.first + "," + p.second + ") ");
}
}
// A main method, A* Search algorithm to find the shortest path
void aStarSearch(int[][] grid,
int rows,
int cols,
Pair src,
Pair dest)
{
if (!isValid(grid, rows, cols, src)) {
System.out.println("Source is invalid...");
return;
}
if (!isValid(grid, rows, cols, dest)) {
System.out.println("Destination is invalid...");
return;
}
if (!isUnBlocked(grid, rows, cols, src)
|| !isUnBlocked(grid, rows, cols, dest)) {
System.out.println("Source or destination is blocked...");
return;
}
if (isDestination(src, dest)) {
System.out.println("We're already (t)here...");
return;
}
boolean[][] closedList = new boolean[rows][cols];//our closed list
Cell[][] cellDetails = new Cell[rows][cols];
int i, j;
// Initialising of the starting cell
i = src.first;
j = src.second;
cellDetails[i][j] = new Cell();
cellDetails[i][j].f = 0.0;
cellDetails[i][j].g = 0.0;
cellDetails[i][j].h = 0.0;
cellDetails[i][j].parent = new Pair( i, j );
// Creating an open list
PriorityQueue<Details> openList = new PriorityQueue<>((o1, o2) -> (int) Math.round(o1.value - o2.value));
// Put the starting cell on the open list, set f.startCell = 0
openList.add(new Details(0.0, i, j));
while (!openList.isEmpty()) {
Details p = openList.peek();
// Add to the closed list
i = p.i; // second element of tuple
j = p.j; // third element of tuple
// Remove from the open list
openList.poll();
closedList[i][j] = true;
// Generating all the 8 neighbors of the cell
for (int addX = -1; addX <= 1; addX++) {
for (int addY = -1; addY <= 1; addY++) {
Pair neighbour = new Pair(i + addX, j + addY);
if (isValid(grid, rows, cols, neighbour)) {
if(cellDetails[neighbour.first] == null){ cellDetails[neighbour.first] = new Cell[cols]; }
if (cellDetails[neighbour.first][neighbour.second] == null) {
cellDetails[neighbour.first][neighbour.second] = new Cell();
}
if (isDestination(neighbour, dest)) {
cellDetails[neighbour.first][neighbour.second].parent = new Pair ( i, j );
System.out.println("The destination cell is found");
tracePath(cellDetails, rows, cols, dest);
return;
}
else if (!closedList[neighbour.first][neighbour.second]
&& isUnBlocked(grid, rows, cols, neighbour)) {
double gNew, hNew, fNew;
gNew = cellDetails[i][j].g + 1.0;
hNew = calculateHValue(neighbour, dest);
fNew = gNew + hNew;
if (cellDetails[neighbour.first][neighbour.second].f == -1
|| cellDetails[neighbour.first][neighbour.second].f > fNew) {
openList.add(new Details(fNew, neighbour.first, neighbour.second));
// Update the details of this
// cell
cellDetails[neighbour.first][neighbour.second].g = gNew;
//heuristic function cellDetails[neighbour.first][neighbour.second].h = hNew;
cellDetails[neighbour.first][neighbour.second].f = fNew;
cellDetails[neighbour.first][neighbour.second].parent = new Pair( i, j );
}
}
}
}
}
}
System.out.println("Failed to find the Destination Cell");
}
// test
public static void main(String[] args) {
//0: The cell is blocked
// 1: The cell is not blocked
int[][] grid = {
{ 1, 1, 0, 0, 1, 0, 0, 0 },
{ 1, 0, 0, 1, 1, 0, 1, 0 },
{ 1, 1, 0, 1, 0, 0, 1, 0 },
{ 1, 1, 0, 1, 1, 1, 1, 1 },
{ 1, 1, 0, 0, 0, 1, 1, 1 },
{ 0, 1, 1, 1, 0, 1, 1, 0 },
{ 1, 1, 0, 1, 1, 1, 1, 0 },
{ 0, 1, 1, 1, 1, 1, 1, 1 }
};
// Start is the left-most upper-most corner
Pair src = new Pair(0,0);
//(8, 0);
// Destination is the right-most bottom-most corner
Pair dest = new Pair(6, 6);
AAsterisk app = new AAsterisk();
app.aStarSearch(grid, grid.length , grid[0].length, src, dest);
}
}
Ang Landas: -> (0,0) -> (1,0) -> (2,1) -> (3,1) -> (4,1) -> (5,2) -> (5, 3) -> (6,4) -> (6,5) -> (6,6)
Makikita na isa ito sa ilang pinakamaikling landas na maaaring itayo sa pagitan ng dalawang puntong ito. Tandaan na ang ikaanim na hakbang sa aming halimbawa sa larawan at sa output ng programa ay naiiba, kahit na ang mga landas ay naging pantay na epektibo. Pinipili ng programa ang isa sa maraming pinakamabisang opsyon.
GO TO FULL VERSION