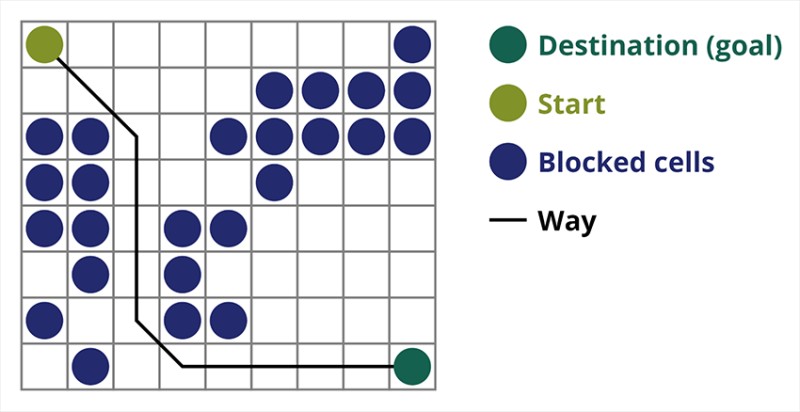
Algoritma carian yang berbeza disesuaikan untuk tugas yang berbeza. Hari ini kita akan bercakap tentang carian A*, salah satu algoritma pencarian laluan yang paling berkesan. Yang ini sangat sesuai untuk permainan komputer dan membina graf carian seperti jalan antara bandar dan sebagainya. Anda mungkin perasan, sebagai contoh, dalam permainan video strategik atau taktikal, bagaimana selepas menekan butang, pemain atau kumpulan anda bermula serta-merta tanpa berlengah-lengah untuk merentas padang ke titik yang anda tentukan. Tidak ada kelewatan dengan tepat kerana permainan menggunakan algoritma berkesan yang mengira dengan tepat bagaimana pemain perlu pergi ke suatu tempat. Atau musuh yang tidak silap mencari pemain dan mula berjalan ke arah yang betul dari jauh. Biasanya, algoritma A* digunakan untuk tindakan sedemikian.
Apakah algoritma A*
Algoritma Pencarian Laluan A* ialah contoh algoritma carian terbaik pertama. Tujuan algoritma A* adalah untuk mencari laluan dari satu titik ke titik yang lain. Ia adalah salah satu klasik untuk mencari algoritma graf. Mari kita fikirkan cara ia berfungsi menggunakan contoh. Bayangkan permainan 2D dengan paparan atas ke bawah. Mari bahagikan kawasan permainan kita kepada ketamakan persegi, contohnya 8*8 sel seperti papan catur. Sel kita boleh menjadi salah satu daripada dua jenis, boleh dilalui atau tidak boleh dilalui (halangan). Setiap tempoh masa pemain atau musuh yang mendekati pemain menggerakkan satu sel. Dalam permainan, sel boleh dilalui boleh mempunyai sifat yang berbeza, contohnya, jalan rata, rumput atau pasir, yang menentukan kesukaran bergerak di sepanjang mereka, tetapi untuk kesederhanaan kita akan menganggap bahawa semua sel boleh dilalui dilalui dengan cara yang sama. Dalam gambar di bawah, sel biru adalah halangan.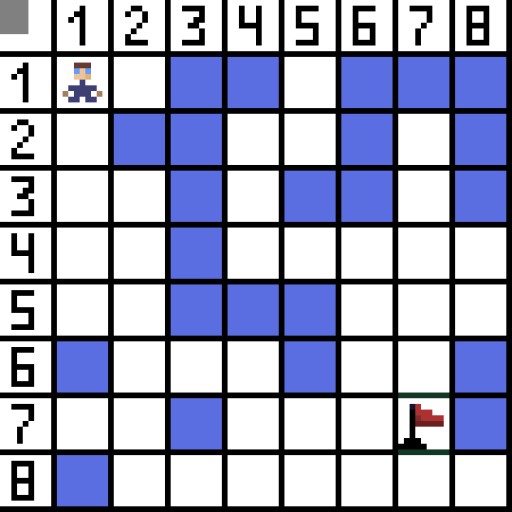
Mari kita tetapkan satu sel (atau nod) sebagai sel permulaan (karakter ada di dalamnya), dan sel lain sebagai sel sasaran atau matlamat (yang mempunyai bendera), dan terangkan cara algoritma A* berfungsi untuk kes ini. Watak berada dalam sel (1,1) dan sasaran berada dalam sel (7,7). Setiap sel mempunyai jiran mendatar, menegak dan pepenjuru. Ia bergantung kepada permainan, jika kita mengira nod pepenjuru atau tidak. Contohnya dalam banyak permainan paparan atas ke bawah seperti Bomberman atau Pacman watak-watak boleh bergerak hanya secara mendatar atau menegak. Dalam kes ini, setiap nod, kecuali menyentuh tepi, hanya mempunyai 4 jiran. Jika kita bercakap tentang permainan di mana watak boleh bergerak secara menyerong, setiap nod boleh mempunyai sehingga 8 jiran. Pada langkah pertama algoritma, sel di mana watak berada mempunyai dua jiran. Lebih tepat lagi, tiga, tetapi satu daripadanya adalah halangan. 
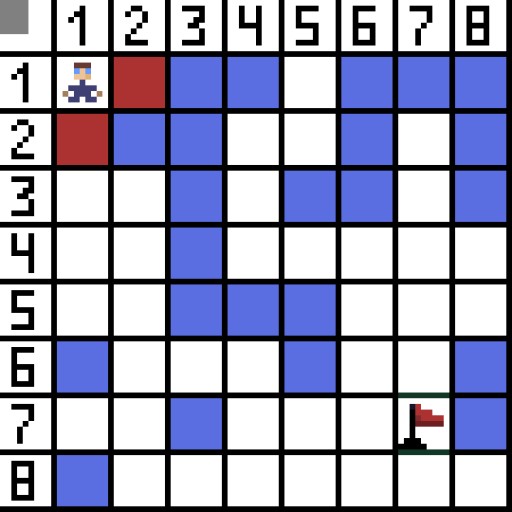Adalah jelas bahawa cara pepenjuru lebih panjang. jika kita menetapkan sisi sel kita untuk bersyarat sama dengan satu, maka panjang pepenjuru sel ini adalah sama dengan punca kuasa dua dua. Inilah yang dikatakan teorem Pythagoras. Untuk pergi dari sel A ke sel B, anda mesti terlebih dahulu memilih salah satu sel yang bersebelahan, dan kemudian yang seterusnya, dan seterusnya. Selain itu, di sepanjang jalan, fahami sama ada adalah mungkin untuk mendapatkan dari sel awal ke sasaran. Algoritma A* pada setiap langkah memilih salah satu sel jiran mengikut nilai fungsi F. Fungsi ini mengukur sejauh mana sel calon boleh dimasukkan dalam laluan terpendek kami. Ini ialah fungsi kos, dan ia adalah jumlah bagi fungsi gerak G dan fungsi heuristik.
-
Kos G — ialah jarak dari nod permulaan.
-
Kos H (Heuristik) ialah jarak dari nod akhir (matlamat). Fungsi ini boleh berbeza, pembangun memutuskan apa yang lebih baik. Mungkin pilihan H adalah yang paling penting dalam A*, dan inilah titik yang menjadikan mana-mana pelaksanaan tertentu algoritma lebih atau kurang berkesan. Secara teorinya anda boleh menggunakan mana-mana fungsi yang anda mahukan.
Dalam kes kita, kita tahu kedudukan sel sasaran dan boleh, sebagai contoh, mengira jarak Euclidean geometri antara sasaran dan sel semasa. Semakin pendek jarak, semakin dekat kita dengan matlamat.
-
Kos F = G + H. Jadi algoritma mengira semua kos F nod jiran dan memilih salah satu kos F terendah untuk dilihat terlebih dahulu. Apabila kami memilih satu, kami menandakannya sebagai ditutup dan mengira nilai untuk jiran nod ini.
Fungsi heuristikBagaimana kita boleh mengira H?
Ini adalah fungsi heuristik. Nama itu sendiri bermaksud bahawa ia ditentukan oleh pengalaman, dan mungkin berbeza. Di sini kita akan mengambilnya sama dengan apa yang dipanggil jarak Euclidean antara titik (x1, y1) dan (x2, y2):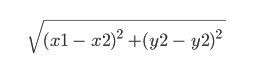
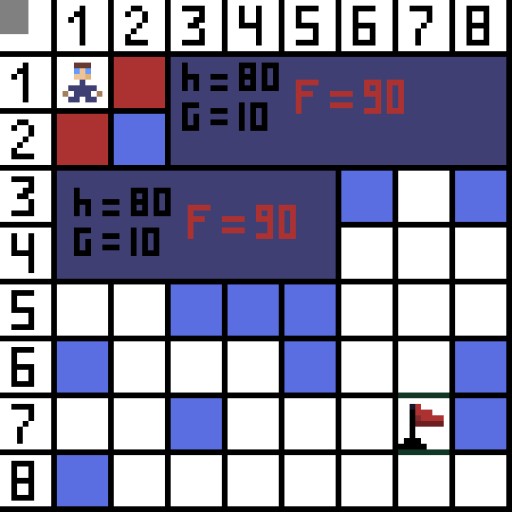Dalam gambar, untuk langkah pertama, terdapat dua pilihan, dan ia adalah sama dalam kos, tetapi pada langkah seterusnya, watak itu menemui jalan buntu dalam salah satu pilihan. Oleh itu, kita pergi ke arah lain. Dalam lelaran seterusnya, kita sudah mempunyai 4 pilihan. 
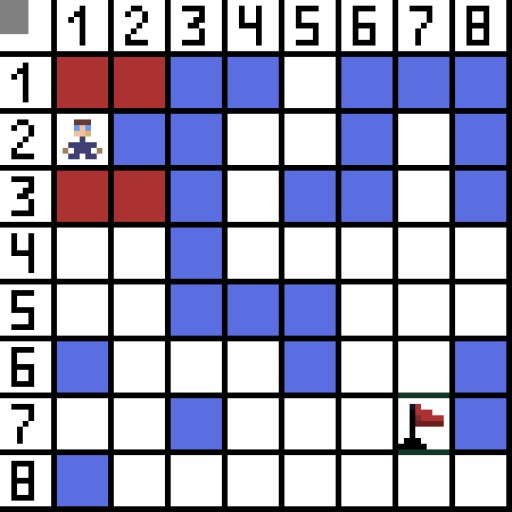Dua daripada mereka tidak sesuai, kerana mereka memimpin ke belakang, dan pilihan lain adalah sama baik, tetapi algoritma memutuskan bahawa adalah yang terbaik untuk pergi secara menyerong ke sel (3,2). Selanjutnya, pada setiap langkah, pengiraan fungsi F diulang sehingga aksara mencapai sel sasaran. Jika, sudah tentu, petikan sedemikian wujud. 
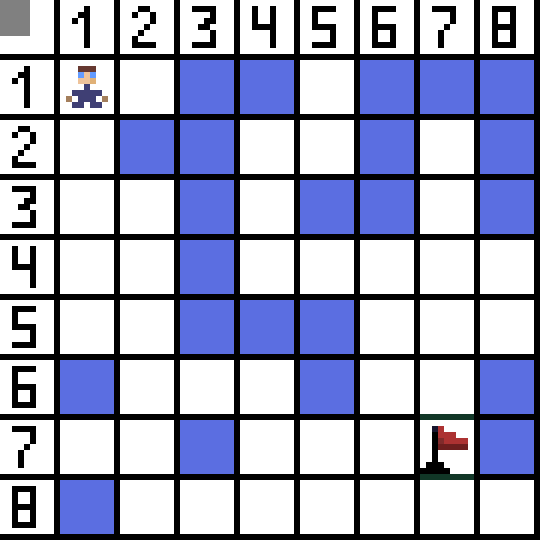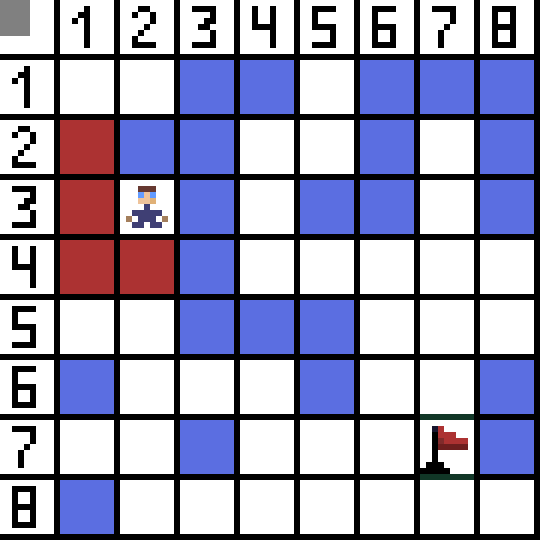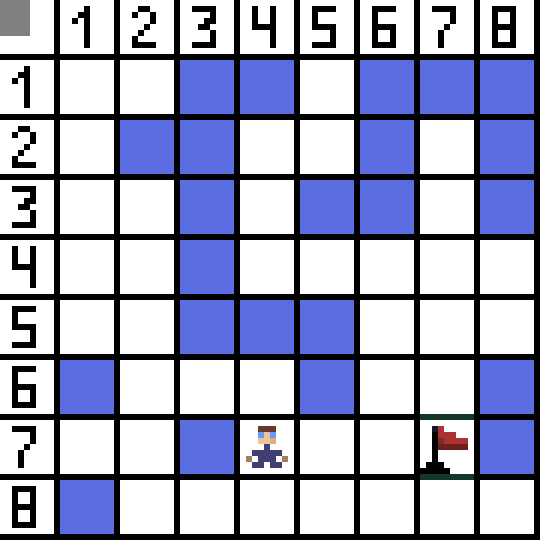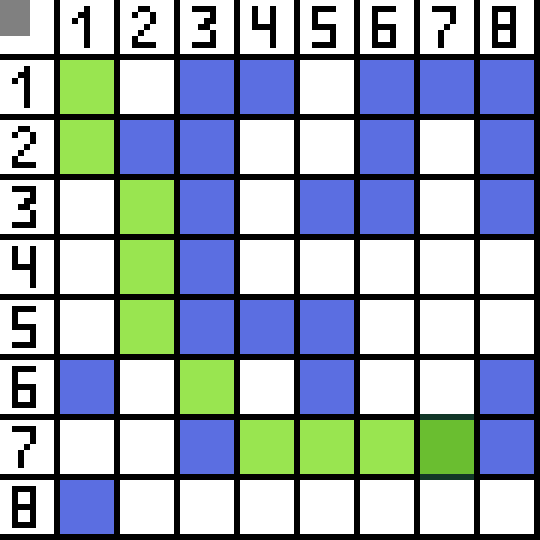Jalan hijau pada gambar gif menunjukkan laluan optimum watak ke bendera.
A* Algoritma langkah demi langkah
Untuk melaksanakan algoritma dalam Java, anda perlu mengambil langkah berikut 1. Mula-mula anda perlu membuat dua senarai, untuk nod terbuka dan nod tertutup. 2. Mulakan kedua-dua senarai. Dalam senarai tertutup, nod mula menghala ke senarai terbuka. 3. manakala terdapat elemen dalam senarai terbuka: 3a. Cari nod min dengan F 3b terkecil. Alih keluar min daripada senarai terbuka 3c. Tentukan jiran min (sehingga 8, jika pepenjuru diambil kira) 3d. Memeriksa setiap jiran: a) jika jiran adalah sel sasaran, hentikan carian b) Jika tidak, hitung G, H untuknya. G = min.G + jarak antara jiran dan min F = G + H c) jika nod dengan kedudukan yang sama dengan jiran berada dalam senarai terbuka dan Fnya kurang daripada jiran, langkau jiran itu d) jika nod dengan kedudukan yang sama dengan jiran berada dalam senarai tertutup, dan fnya kurang daripada jiran, langkau jiran itu. Jika tidak, tambahkan nod pada senarai terbuka Tamat gelung dalam 3e. Menambah min pada senarai tertutup Akhir gelung luar Jadi, pada setiap lelaran kita akan melakukan yang seterusnya:- Pilih sel daripada senarai terbuka kami dengan jumlah skor anggaran terendah.
- Alih keluar sel ini daripada senarai terbuka.
- Tambahkan semua sel yang boleh kita capai daripadanya ke senarai terbuka.
- Apabila kami melakukan ini, kami turut memproses skor baharu daripada nod itu kepada setiap nod baharu untuk melihat sama ada ia adalah peningkatan pada apa yang kami ada setakat ini, dan jika ya, kami mengemas kini perkara yang kami ketahui tentang sel itu.
A* Pseudokod
Berikut ialah pseudokod ringkas pencarian laluan A*:Input: a grid with locked and empty cells, with start and goal cell.
Output: least cost path from start to goal cell.
Initialisation
openList = {startCell} //list of traversed cells
closedList = {} //list of already traversed cells
g.startCell = 0 //cost from source cell to a cell
h.startCell = h(startCell, goal) //heuristic
f.startCell = g.startCell + h.StartCell
while openList is not empty
do
//let the currentCell equal the cell with the least f value
currentCell = Cell on top of openList, with least f
if currentCell == end return
remove currentCell from openList
add currentCell to closedList
foreach n in child.currentCell
if n in closedList
continue
cost = g.currentCell + distance(currentCell,n)
if (n in openList and cost < g.n)
remove n from closedList
g.n = cost
h.n = h(n, goal)
f.n = g.n + h.nDaripada pseudokod kepada A* Pelaksanaan di Jawa
A* Pathfinding dalam realisasi Java harus mempunyai beberapa kaedah untuk melayani algoritma:- Sel, struktur untuk memegang parameter yang diperlukan
- Senarai terbuka dan tertutup
- Kaedah untuk mengira fungsi heuristik
- Kaedah untuk mengesan laluan dari sumber ke destinasi
- Kaedah untuk menyemak sama ada sel yang diberikan disekat, jika ia sudah dicapai, jika ia sah dan sebagainya
package Asterist;
import java.util.PriorityQueue;
import java.util.Stack;
public class AAsterisk {
//Java Program to implement A* Search Algorithm
//Here we're creating a shortcut for (int, int) pair
public static class Pair {
int first;
int second;
public Pair(int first, int second){
this.first = first;
this.second = second;
}
@Override
public boolean equals(Object obj) {
return obj instanceof Pair && this.first == ((Pair)obj).first && this.second == ((Pair)obj).second;
}
}
// Creating a shortcut for tuple<int, int, int> type
public static class Details {
double value;
int i;
int j;
public Details(double value, int i, int j) {
this.value = value;
this.i = i;
this.j = j;
}
}
// a Cell (node) structure
public static class Cell {
public Pair parent;
// f = g + h, where h is heuristic
public double f, g, h;
Cell()
{
parent = new Pair(-1, -1);
f = -1;
g = -1;
h = -1;
}
public Cell(Pair parent, double f, double g, double h) {
this.parent = parent;
this.f = f;
this.g = g;
this.h = h;
}
}
// method to check if our cell (row, col) is valid
boolean isValid(int[][] grid, int rows, int cols,
Pair point)
{
if (rows > 0 && cols > 0)
return (point.first >= 0) && (point.first < rows)
&& (point.second >= 0)
&& (point.second < cols);
return false;
}
//is the cell blocked?
boolean isUnBlocked(int[][] grid, int rows, int cols,
Pair point)
{
return isValid(grid, rows, cols, point)
&& grid[point.first][point.second] == 1;
}
//Method to check if destination cell has been already reached
boolean isDestination(Pair position, Pair dest)
{
return position == dest || position.equals(dest);
}
// Method to calculate heuristic function
double calculateHValue(Pair src, Pair dest)
{
return Math.sqrt(Math.pow((src.first - dest.first), 2.0) + Math.pow((src.second - dest.second), 2.0));
}
// Method for tracking the path from source to destination
void tracePath(
Cell[][] cellDetails,
int cols,
int rows,
Pair dest)
{ //A* Search algorithm path
System.out.println("The Path: ");
Stack<Pair> path = new Stack<>();
int row = dest.first;
int col = dest.second;
Pair nextNode = cellDetails[row][col].parent;
do {
path.push(new Pair(row, col));
nextNode = cellDetails[row][col].parent;
row = nextNode.first;
col = nextNode.second;
} while (cellDetails[row][col].parent != nextNode); // until src
while (!path.empty()) {
Pair p = path.peek();
path.pop();
System.out.println("-> (" + p.first + "," + p.second + ") ");
}
}
// A main method, A* Search algorithm to find the shortest path
void aStarSearch(int[][] grid,
int rows,
int cols,
Pair src,
Pair dest)
{
if (!isValid(grid, rows, cols, src)) {
System.out.println("Source is invalid...");
return;
}
if (!isValid(grid, rows, cols, dest)) {
System.out.println("Destination is invalid...");
return;
}
if (!isUnBlocked(grid, rows, cols, src)
|| !isUnBlocked(grid, rows, cols, dest)) {
System.out.println("Source or destination is blocked...");
return;
}
if (isDestination(src, dest)) {
System.out.println("We're already (t)here...");
return;
}
boolean[][] closedList = new boolean[rows][cols];//our closed list
Cell[][] cellDetails = new Cell[rows][cols];
int i, j;
// Initialising of the starting cell
i = src.first;
j = src.second;
cellDetails[i][j] = new Cell();
cellDetails[i][j].f = 0.0;
cellDetails[i][j].g = 0.0;
cellDetails[i][j].h = 0.0;
cellDetails[i][j].parent = new Pair( i, j );
// Creating an open list
PriorityQueue<Details> openList = new PriorityQueue<>((o1, o2) -> (int) Math.round(o1.value - o2.value));
// Put the starting cell on the open list, set f.startCell = 0
openList.add(new Details(0.0, i, j));
while (!openList.isEmpty()) {
Details p = openList.peek();
// Add to the closed list
i = p.i; // second element of tuple
j = p.j; // third element of tuple
// Remove from the open list
openList.poll();
closedList[i][j] = true;
// Generating all the 8 neighbors of the cell
for (int addX = -1; addX <= 1; addX++) {
for (int addY = -1; addY <= 1; addY++) {
Pair neighbour = new Pair(i + addX, j + addY);
if (isValid(grid, rows, cols, neighbour)) {
if(cellDetails[neighbour.first] == null){ cellDetails[neighbour.first] = new Cell[cols]; }
if (cellDetails[neighbour.first][neighbour.second] == null) {
cellDetails[neighbour.first][neighbour.second] = new Cell();
}
if (isDestination(neighbour, dest)) {
cellDetails[neighbour.first][neighbour.second].parent = new Pair ( i, j );
System.out.println("The destination cell is found");
tracePath(cellDetails, rows, cols, dest);
return;
}
else if (!closedList[neighbour.first][neighbour.second]
&& isUnBlocked(grid, rows, cols, neighbour)) {
double gNew, hNew, fNew;
gNew = cellDetails[i][j].g + 1.0;
hNew = calculateHValue(neighbour, dest);
fNew = gNew + hNew;
if (cellDetails[neighbour.first][neighbour.second].f == -1
|| cellDetails[neighbour.first][neighbour.second].f > fNew) {
openList.add(new Details(fNew, neighbour.first, neighbour.second));
// Update the details of this
// cell
cellDetails[neighbour.first][neighbour.second].g = gNew;
//heuristic function cellDetails[neighbour.first][neighbour.second].h = hNew;
cellDetails[neighbour.first][neighbour.second].f = fNew;
cellDetails[neighbour.first][neighbour.second].parent = new Pair( i, j );
}
}
}
}
}
}
System.out.println("Failed to find the Destination Cell");
}
// test
public static void main(String[] args) {
//0: The cell is blocked
// 1: The cell is not blocked
int[][] grid = {
{ 1, 1, 0, 0, 1, 0, 0, 0 },
{ 1, 0, 0, 1, 1, 0, 1, 0 },
{ 1, 1, 0, 1, 0, 0, 1, 0 },
{ 1, 1, 0, 1, 1, 1, 1, 1 },
{ 1, 1, 0, 0, 0, 1, 1, 1 },
{ 0, 1, 1, 1, 0, 1, 1, 0 },
{ 1, 1, 0, 1, 1, 1, 1, 0 },
{ 0, 1, 1, 1, 1, 1, 1, 1 }
};
// Start is the left-most upper-most corner
Pair src = new Pair(0,0);
//(8, 0);
// Destination is the right-most bottom-most corner
Pair dest = new Pair(6, 6);
AAsterisk app = new AAsterisk();
app.aStarSearch(grid, grid.length , grid[0].length, src, dest);
}
}
Laluan: -> (0,0) -> (1,0) -> (2,1) -> (3,1) -> (4,1) -> (5,2) -> (5, 3) -> (6,4) -> (6,5) -> (6,6)
Ia boleh dilihat bahawa ini adalah salah satu daripada beberapa laluan terpendek yang boleh dibina antara dua titik ini. Perhatikan bahawa langkah keenam dalam contoh kami dalam gambar dan dalam output program adalah berbeza, walaupun laluannya ternyata sama berkesan. Program ini memilih salah satu daripada banyak pilihan yang paling berkesan.
GO TO FULL VERSION