Các thuật toán tìm kiếm khác nhau được điều chỉnh cho các nhiệm vụ khác nhau. Hôm nay chúng ta sẽ nói về tìm kiếm A*, một trong những thuật toán tìm đường hiệu quả nhất. Cái này rất phù hợp cho các trò chơi trên máy tính và xây dựng các biểu đồ tìm kiếm như đường đi giữa các thành phố, v.v. Ví dụ: bạn có thể nhận thấy trong trò chơi điện tử chiến lược hoặc chiến thuật, sau khi nhấn nút, người chơi hoặc nhóm của bạn bắt đầu ngay lập tức băng qua sân đến điểm bạn đã chỉ định ngay lập tức. Chính xác là không có độ trễ vì trò chơi sử dụng các thuật toán hiệu quả để tính toán chính xác cách người chơi cần đến một nơi nào đó. Hoặc một kẻ thù không thể nhầm lẫn tìm thấy người chơi và bắt đầu đi đúng hướng từ xa. Thông thường, thuật toán A* được sử dụng cho những hành động như vậy.
Thuật toán A* là gì
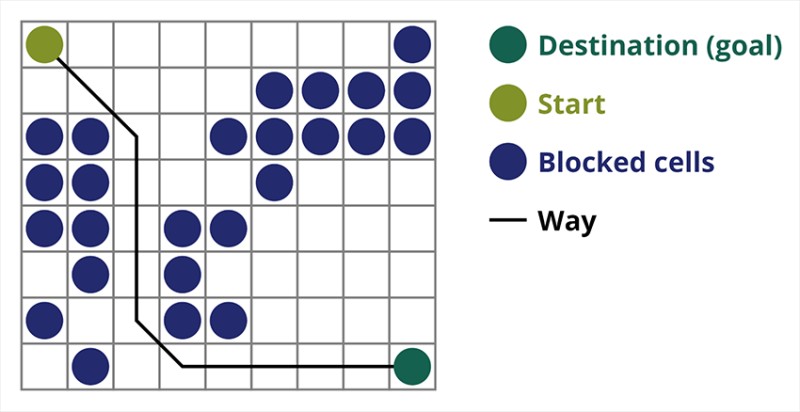
Thuật toán tìm đường A* là một ví dụ về thuật toán tìm kiếm tốt nhất đầu tiên. Mục đích của thuật toán A* là tìm đường đi từ điểm này đến điểm khác. Đó là một trong những tác phẩm kinh điển để tìm kiếm các thuật toán đồ thị. Hãy tìm hiểu cách nó hoạt động bằng cách sử dụng một ví dụ. Hãy tưởng tượng một trò chơi 2D với góc nhìn từ trên xuống. Hãy chia khu vực trò chơi của chúng ta thành các ô vuông tham lam, ví dụ 8*8 ô như bàn cờ. Các tế bào của chúng ta có thể là một trong hai loại, có thể vượt qua hoặc không thể vượt qua (chướng ngại vật). Mỗi khoảng thời gian người chơi hoặc kẻ thù tiếp cận người chơi sẽ di chuyển một ô. Trong trò chơi, các ô có thể đi qua có thể có bản chất khác, chẳng hạn như đường bằng phẳng, cỏ hoặc cát, điều này quyết định độ khó khi di chuyển dọc theo chúng, nhưng để đơn giản, chúng tôi giả định rằng tất cả các ô có thể đi qua đều được đi qua theo cùng một cách. Trong hình bên dưới, các ô màu xanh là chướng ngại vật.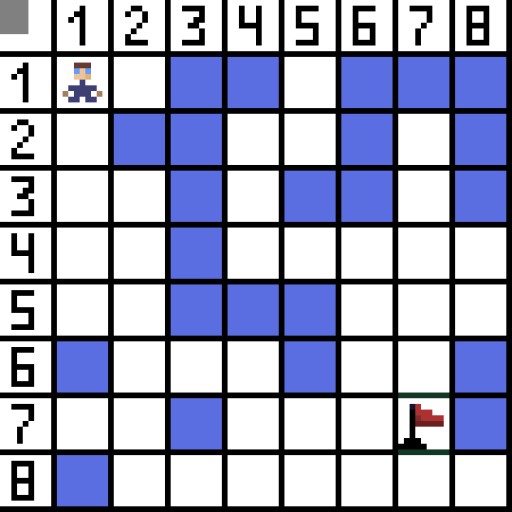
Hãy chỉ định một ô (hoặc nút) làm ô bắt đầu (ký tự nằm trong đó) và ô còn lại làm ô đích hoặc ô mục tiêu (ô có cờ) và mô tả cách hoạt động của thuật toán A* trong trường hợp này. Ký tự nằm trong ô (1,1) và đích nằm trong ô (7,7). Mỗi ô có các hàng xóm ngang, dọc và chéo. Nó phụ thuộc vào trò chơi, liệu chúng ta có tính toán các nút chéo hay không. Ví dụ: trong nhiều trò chơi có góc nhìn từ trên xuống như Bomberman hay Pacman, các nhân vật chỉ có thể di chuyển theo chiều ngang hoặc chiều dọc. Trong trường hợp này, mọi nút, ngoại trừ việc chạm vào các cạnh, chỉ có 4 nút lân cận. Nếu chúng ta đang nói về một trò chơi mà các nhân vật có thể di chuyển theo đường chéo thì mỗi nút có thể có tối đa 8 nút lân cận. Ở bước đầu tiên của thuật toán, ô chứa ký tự có hai ô lân cận. Chính xác hơn là ba, nhưng một trong số đó là chướng ngại vật. 
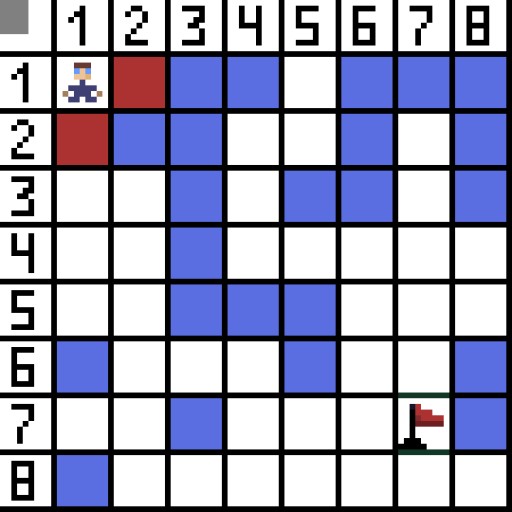Rõ ràng là đường chéo dài hơn. nếu chúng ta đặt cạnh của ô có điều kiện bằng một, thì độ dài đường chéo của ô này bằng căn bậc hai của hai. Đây là những gì định lý Pythagore nói. Để đi từ ô A đến ô B, trước tiên bạn phải chọn một trong các ô lân cận, sau đó chọn ô tiếp theo, v.v. Ngoài ra, trong quá trình thực hiện, hãy tìm hiểu xem liệu có thể đi từ ô ban đầu đến ô mục tiêu hay không. Thuật toán A* ở mỗi bước sẽ chọn một trong các ô lân cận theo giá trị của hàm F. Hàm này đo lường mức độ tốt của một ô ứng cử viên được đưa vào đường đi ngắn nhất của chúng ta. Đây là hàm chi phí và là tổng của hàm di chuyển G và hàm heuristic.
-
Chi phí G - là khoảng cách từ nút bắt đầu.
-
Chi phí H (Heuristic) là khoảng cách từ nút cuối (mục tiêu). Chức năng này có thể khác, nhà phát triển sẽ quyết định cái nào tốt hơn. Có lẽ việc lựa chọn H là quan trọng nhất trong A*, và đây là điểm làm cho bất kỳ việc triển khai cụ thể nào của thuật toán ít nhiều có hiệu quả. Về mặt lý thuyết bạn có thể sử dụng bất kỳ chức năng nào bạn muốn.
Trong trường hợp của chúng tôi, chúng tôi biết vị trí của ô mục tiêu và có thể tính toán khoảng cách Euclide hình học giữa ô đích và ô hiện tại. Khoảng cách càng ngắn thì chúng ta càng đến gần mục tiêu.
-
Chi phí F = G + H. Vì vậy, thuật toán tính toán chi phí F của tất cả các nút lân cận và chọn một trong những chi phí F thấp nhất để xem xét đầu tiên. Khi chúng tôi chọn một nút, chúng tôi đánh dấu nó là đã đóng và tính toán các giá trị cho nút lân cận này.
Hàm heuristicLàm thế nào chúng ta có thể tính H?
Đây là một chức năng heuristic. Bản thân tên có nghĩa là nó được xác định bằng kinh nghiệm và có thể khác. Ở đây chúng ta sẽ lấy nó bằng cái gọi là khoảng cách Euclide giữa các điểm (x1, y1) và (x2, y2):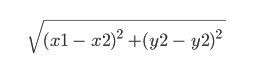
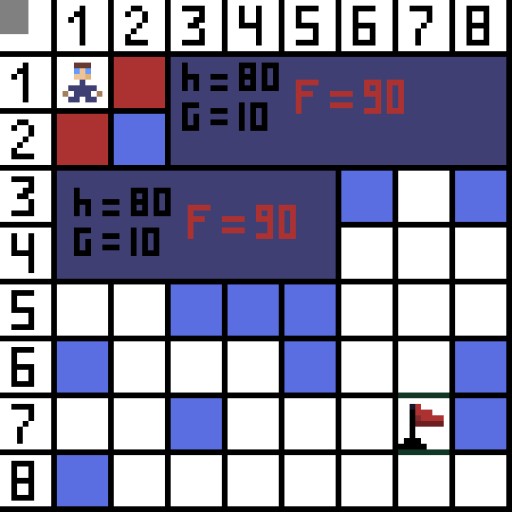Trong hình, ở bước đầu tiên, có hai tùy chọn và chúng giống nhau về chi phí, nhưng ở bước tiếp theo, nhân vật rơi vào ngõ cụt ở một trong các lựa chọn. Vì vậy, chúng tôi đang đi theo con đường khác. Trong lần lặp tiếp theo, chúng tôi đã có 4 lựa chọn. 
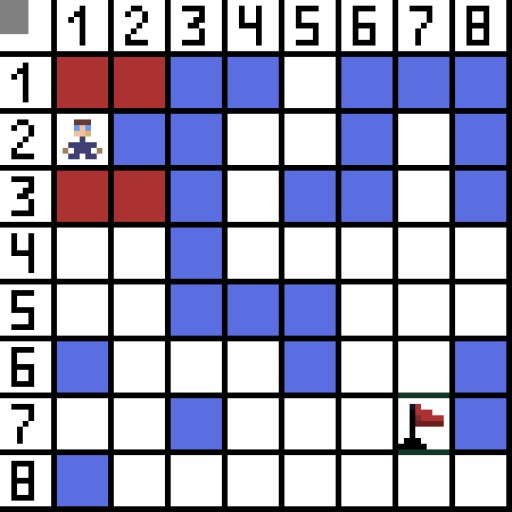Hai trong số đó không phù hợp vì chúng dẫn ngược lại và các tùy chọn khác đều tốt như nhau, nhưng thuật toán quyết định rằng tốt nhất nên đi theo đường chéo đến ô (3,2). Hơn nữa, ở mỗi bước, việc tính toán hàm F được lặp lại cho đến khi ký tự đến ô đích. Tất nhiên, nếu một đoạn văn như vậy tồn tại. 
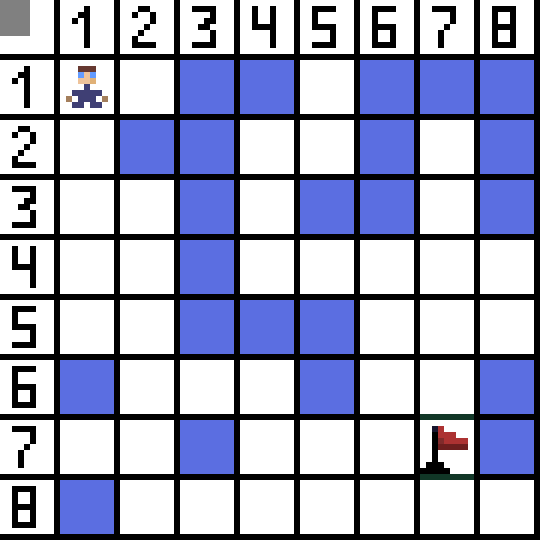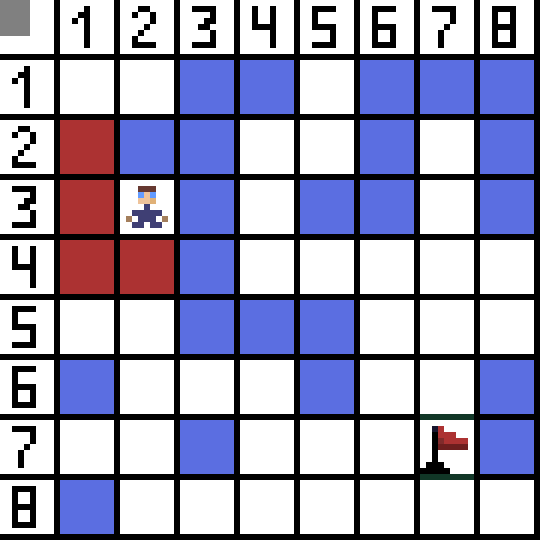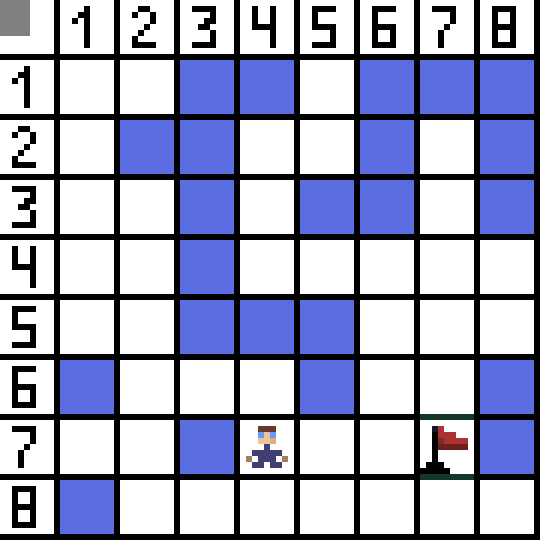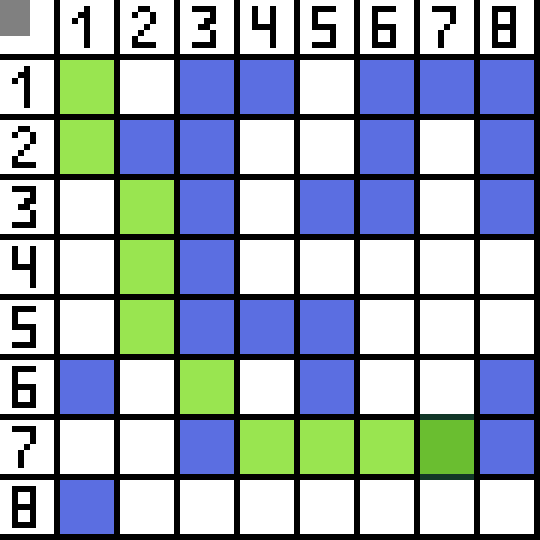Đường màu xanh lá cây trên ảnh gif biểu thị đường đi tối ưu của nhân vật đến lá cờ.
Thuật toán A* từng bước
Để triển khai thuật toán trong Java, bạn cần thực hiện các bước sau 1. Đầu tiên bạn cần tạo hai danh sách, cho các nút mở và các nút đóng. 2. Khởi tạo cả hai danh sách. Trong danh sách đóng, nút bắt đầu trỏ đến danh sách mở. 3. khi có các phần tử trong danh sách mở: 3a. Tìm nút min có F 3b nhỏ nhất. Xóa min khỏi danh sách mở 3c. Xác định các lân cận tối thiểu (tối đa 8, nếu tính đến đường chéo) 3d. Kiểm tra từng ô lân cận: a) nếu lân cận đó là ô mục tiêu, dừng tìm kiếm b) Nếu không, hãy tính G, H cho ô đó. G = min.G + khoảng cách giữa hàng xóm và min F = G + H c) nếu nút có cùng vị trí với hàng xóm nằm trong danh sách mở và F của nó nhỏ hơn hàng xóm đó, bỏ qua hàng xóm đó d) nếu nút có cùng vị trí với nút lân cận nằm trong danh sách đóng và f của nó nhỏ hơn nút lân cận đó thì bỏ qua nút lân cận đó. Nếu không, hãy thêm nút vào danh sách mở Kết thúc vòng lặp bên trong 3e. Thêm min vào danh sách đóng Kết thúc vòng lặp ngoài Vì vậy, tại mỗi lần lặp, chúng ta sẽ thực hiện bước tiếp theo:- Chọn ô từ danh sách mở của chúng tôi có tổng điểm ước tính thấp nhất.
- Xóa ô này khỏi danh sách mở.
- Thêm tất cả các ô mà chúng ta có thể tiếp cận từ nó vào danh sách mở.
- Khi thực hiện việc này, chúng tôi cũng xử lý điểm mới từ nút đó sang từng nút mới để xem liệu đó có phải là sự cải thiện so với những gì chúng tôi có cho đến nay hay không và nếu có thì chúng tôi sẽ cập nhật những gì chúng tôi biết về ô đó.
A* Mã giả
Đây là mã giả ngắn gọn của việc tìm đường A*:Input: a grid with locked and empty cells, with start and goal cell.
Output: least cost path from start to goal cell.
Initialisation
openList = {startCell} //list of traversed cells
closedList = {} //list of already traversed cells
g.startCell = 0 //cost from source cell to a cell
h.startCell = h(startCell, goal) //heuristic
f.startCell = g.startCell + h.StartCell
while openList is not empty
do
//let the currentCell equal the cell with the least f value
currentCell = Cell on top of openList, with least f
if currentCell == end return
remove currentCell from openList
add currentCell to closedList
foreach n in child.currentCell
if n in closedList
continue
cost = g.currentCell + distance(currentCell,n)
if (n in openList and cost < g.n)
remove n from closedList
g.n = cost
h.n = h(n, goal)
f.n = g.n + h.nTừ mã giả đến triển khai A* trong Java
A* Tìm đường trong hiện thực hóa Java cần có một số phương thức để phục vụ thuật toán:- Ô, một cấu trúc chứa các tham số cần thiết
- Danh sách mở và đóng
- Phương pháp tính hàm heuristic
- Phương pháp dò đường đi từ nguồn đến đích
- Các phương pháp để kiểm tra xem ô đã cho có bị chặn hay không, liệu nó đã đạt đến chưa, liệu nó có hợp lệ hay không, v.v.
package Asterist;
import java.util.PriorityQueue;
import java.util.Stack;
public class AAsterisk {
//Java Program to implement A* Search Algorithm
//Here we're creating a shortcut for (int, int) pair
public static class Pair {
int first;
int second;
public Pair(int first, int second){
this.first = first;
this.second = second;
}
@Override
public boolean equals(Object obj) {
return obj instanceof Pair && this.first == ((Pair)obj).first && this.second == ((Pair)obj).second;
}
}
// Creating a shortcut for tuple<int, int, int> type
public static class Details {
double value;
int i;
int j;
public Details(double value, int i, int j) {
this.value = value;
this.i = i;
this.j = j;
}
}
// a Cell (node) structure
public static class Cell {
public Pair parent;
// f = g + h, where h is heuristic
public double f, g, h;
Cell()
{
parent = new Pair(-1, -1);
f = -1;
g = -1;
h = -1;
}
public Cell(Pair parent, double f, double g, double h) {
this.parent = parent;
this.f = f;
this.g = g;
this.h = h;
}
}
// method to check if our cell (row, col) is valid
boolean isValid(int[][] grid, int rows, int cols,
Pair point)
{
if (rows > 0 && cols > 0)
return (point.first >= 0) && (point.first < rows)
&& (point.second >= 0)
&& (point.second < cols);
return false;
}
//is the cell blocked?
boolean isUnBlocked(int[][] grid, int rows, int cols,
Pair point)
{
return isValid(grid, rows, cols, point)
&& grid[point.first][point.second] == 1;
}
//Method to check if destination cell has been already reached
boolean isDestination(Pair position, Pair dest)
{
return position == dest || position.equals(dest);
}
// Method to calculate heuristic function
double calculateHValue(Pair src, Pair dest)
{
return Math.sqrt(Math.pow((src.first - dest.first), 2.0) + Math.pow((src.second - dest.second), 2.0));
}
// Method for tracking the path from source to destination
void tracePath(
Cell[][] cellDetails,
int cols,
int rows,
Pair dest)
{ //A* Search algorithm path
System.out.println("The Path: ");
Stack<Pair> path = new Stack<>();
int row = dest.first;
int col = dest.second;
Pair nextNode = cellDetails[row][col].parent;
do {
path.push(new Pair(row, col));
nextNode = cellDetails[row][col].parent;
row = nextNode.first;
col = nextNode.second;
} while (cellDetails[row][col].parent != nextNode); // until src
while (!path.empty()) {
Pair p = path.peek();
path.pop();
System.out.println("-> (" + p.first + "," + p.second + ") ");
}
}
// A main method, A* Search algorithm to find the shortest path
void aStarSearch(int[][] grid,
int rows,
int cols,
Pair src,
Pair dest)
{
if (!isValid(grid, rows, cols, src)) {
System.out.println("Source is invalid...");
return;
}
if (!isValid(grid, rows, cols, dest)) {
System.out.println("Destination is invalid...");
return;
}
if (!isUnBlocked(grid, rows, cols, src)
|| !isUnBlocked(grid, rows, cols, dest)) {
System.out.println("Source or destination is blocked...");
return;
}
if (isDestination(src, dest)) {
System.out.println("We're already (t)here...");
return;
}
boolean[][] closedList = new boolean[rows][cols];//our closed list
Cell[][] cellDetails = new Cell[rows][cols];
int i, j;
// Initialising of the starting cell
i = src.first;
j = src.second;
cellDetails[i][j] = new Cell();
cellDetails[i][j].f = 0.0;
cellDetails[i][j].g = 0.0;
cellDetails[i][j].h = 0.0;
cellDetails[i][j].parent = new Pair( i, j );
// Creating an open list
PriorityQueue<Details> openList = new PriorityQueue<>((o1, o2) -> (int) Math.round(o1.value - o2.value));
// Put the starting cell on the open list, set f.startCell = 0
openList.add(new Details(0.0, i, j));
while (!openList.isEmpty()) {
Details p = openList.peek();
// Add to the closed list
i = p.i; // second element of tuple
j = p.j; // third element of tuple
// Remove from the open list
openList.poll();
closedList[i][j] = true;
// Generating all the 8 neighbors of the cell
for (int addX = -1; addX <= 1; addX++) {
for (int addY = -1; addY <= 1; addY++) {
Pair neighbour = new Pair(i + addX, j + addY);
if (isValid(grid, rows, cols, neighbour)) {
if(cellDetails[neighbour.first] == null){ cellDetails[neighbour.first] = new Cell[cols]; }
if (cellDetails[neighbour.first][neighbour.second] == null) {
cellDetails[neighbour.first][neighbour.second] = new Cell();
}
if (isDestination(neighbour, dest)) {
cellDetails[neighbour.first][neighbour.second].parent = new Pair ( i, j );
System.out.println("The destination cell is found");
tracePath(cellDetails, rows, cols, dest);
return;
}
else if (!closedList[neighbour.first][neighbour.second]
&& isUnBlocked(grid, rows, cols, neighbour)) {
double gNew, hNew, fNew;
gNew = cellDetails[i][j].g + 1.0;
hNew = calculateHValue(neighbour, dest);
fNew = gNew + hNew;
if (cellDetails[neighbour.first][neighbour.second].f == -1
|| cellDetails[neighbour.first][neighbour.second].f > fNew) {
openList.add(new Details(fNew, neighbour.first, neighbour.second));
// Update the details of this
// cell
cellDetails[neighbour.first][neighbour.second].g = gNew;
//heuristic function cellDetails[neighbour.first][neighbour.second].h = hNew;
cellDetails[neighbour.first][neighbour.second].f = fNew;
cellDetails[neighbour.first][neighbour.second].parent = new Pair( i, j );
}
}
}
}
}
}
System.out.println("Failed to find the Destination Cell");
}
// test
public static void main(String[] args) {
//0: The cell is blocked
// 1: The cell is not blocked
int[][] grid = {
{ 1, 1, 0, 0, 1, 0, 0, 0 },
{ 1, 0, 0, 1, 1, 0, 1, 0 },
{ 1, 1, 0, 1, 0, 0, 1, 0 },
{ 1, 1, 0, 1, 1, 1, 1, 1 },
{ 1, 1, 0, 0, 0, 1, 1, 1 },
{ 0, 1, 1, 1, 0, 1, 1, 0 },
{ 1, 1, 0, 1, 1, 1, 1, 0 },
{ 0, 1, 1, 1, 1, 1, 1, 1 }
};
// Start is the left-most upper-most corner
Pair src = new Pair(0,0);
//(8, 0);
// Destination is the right-most bottom-most corner
Pair dest = new Pair(6, 6);
AAsterisk app = new AAsterisk();
app.aStarSearch(grid, grid.length , grid[0].length, src, dest);
}
}
Đường dẫn: -> (0,0) -> (1,0) -> (2,1) -> (3,1) -> (4,1) -> (5,2) -> (5, 3) -> (6,4) -> (6,5) -> (6,6)
Có thể thấy rằng đây là một trong những con đường ngắn nhất có thể được xây dựng giữa hai điểm này. Lưu ý rằng bước thứ sáu trong ví dụ của chúng tôi trong hình và trong đầu ra của chương trình là khác nhau, mặc dù các đường dẫn tỏ ra có hiệu quả như nhau. Chương trình chọn một trong nhiều tùy chọn hiệu quả nhất.
GO TO FULL VERSION