不同的搜索算法针对不同的任务而定制。今天我们要讨论的是 A* 搜索，这是最有效的寻路算法之一。这个非常适合电脑游戏和构建搜索图，例如城市之间的道路等。例如，您可能已经注意到，在战略或战术视频游戏中，按下按钮后，您的玩家或团队如何立即开始，毫不拖延地穿过场地到达您指定的点。之所以没有延迟，是因为游戏使用了有效的算法来准确计算玩家需要如何到达某个地方。或者敌人明确地找到了玩家并开始从远处朝正确的方向行走。通常，A*算法用于此类操作。
什么是A*算法
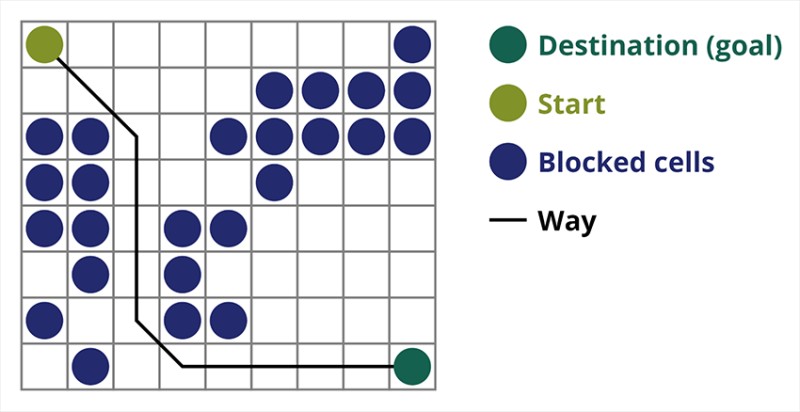
寻路算法 A* 是最佳优先搜索算法的示例。A*算法的目的是找到从一点到另一点的路径。它是搜索图算法的经典之一。让我们通过一个例子来了解它是如何工作的。想象一个具有自上而下视图的 2D 游戏。让我们将游戏区域划分为正方形贪婪，例如像棋盘一样的 8*8 单元格。我们的细胞可以是两种类型之一：可通过的或不可通过的（障碍）。每一段时间，玩家或接近玩家的敌人都会移动一个单元格。在游戏中，可通过的单元可以具有不同的性质，例如平坦的道路、草地或沙子，这决定了沿着它们移动的难度，但为了简单起见，我们假设所有可通过的单元都以相同的方式通过。下图中，蓝色的单元格是障碍物。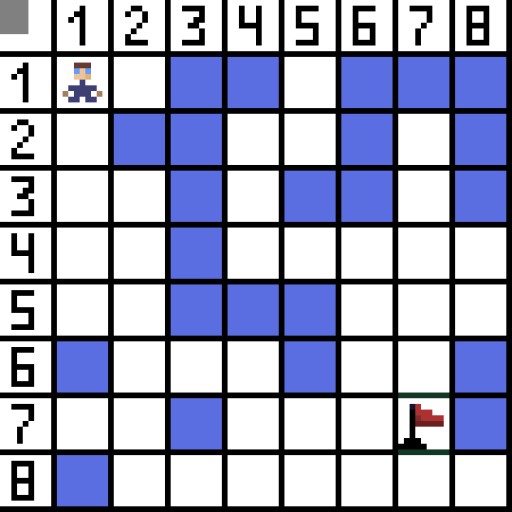
让我们将一个单元格（或节点）指定为起始单元格（角色位于其中），将另一个单元格指定为目标或目标单元格（带有标志的单元格），并描述 A* 算法在这种情况下的工作原理。角色位于单元格 (1,1) 中，目标位于单元格 (7,7) 中。每个单元格都有水平、垂直和对角线的邻居。是否计算对角线节点取决于游戏。例如，在许多自上而下的视图游戏（例如炸弹人或吃豆人）中，角色只能水平或垂直移动。在这种情况下，除了接触边缘之外，每个节点只有 4 个邻居。如果我们谈论的是角色可以沿对角线移动的游戏，则每个节点最多可以有 8 个邻居。在算法的第一步，角色所在的单元格有两个邻居。更准确地说，是三个，但其中一个是障碍。 
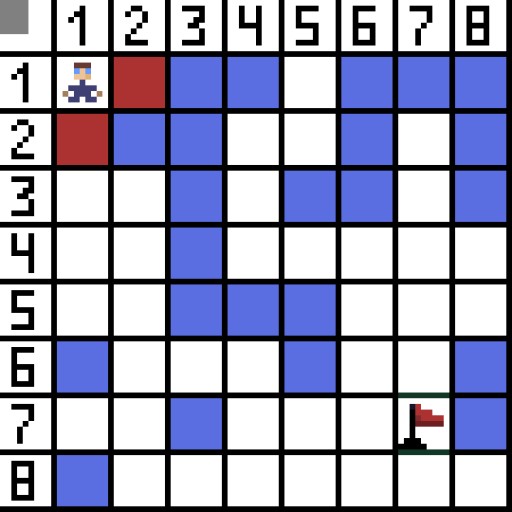很明显，对角线更长。如果我们将单元格的边有条件地设置为等于 1，则该单元格的对角线长度等于 2 的平方根。这就是毕达哥拉斯定理所说的。要从单元格 A 到单元格 B，必须首先选择相邻单元格之一，然后选择下一个，依此类推。另外，在此过程中，了解是否有可能从初始单元格到达目标单元格。A* 算法在每一步都会根据函数 F 的值选择一个相邻小区。该函数测量候选小区包含在我们的最短路径中的程度。这就是成本函数，它是移动函数 G 和启发函数的和。
-
G 成本 — 是距起始节点的距离。
-
H 成本（启发式）是距结束（目标）节点的距离。这个功能可以不同，由开发人员决定哪个更好。也许 H 的选择是 A* 中最重要的，这就是使算法的任何特定实现或多或少有效的一点。理论上你可以使用任何你想要的功能。
在我们的例子中，我们知道目标单元格的位置，并且可以计算目标单元格和当前单元格之间的几何欧几里德距离。距离越短，我们离目标就越近。
-
F 成本 = G + H。因此，算法计算所有邻居节点的 F 成本，并选择 F 成本最低的一个首先查看。当我们选择一个时，我们将其标记为关闭并计算该节点邻居的值。
启发式函数我们如何计算H？
这是一个启发式函数。这个名字本身就意味着它是由经验决定的，并且可以有所不同。这里我们将其等于点 (x1, y1) 和 (x2, y2) 之间的所谓欧几里得距离：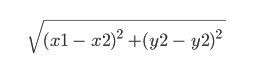
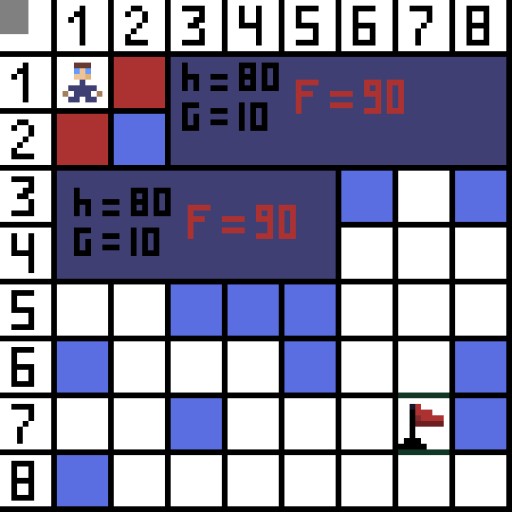图中，对于第一步，有两个选项，它们的成本是相同的，但在下一步中，角色在其中一个选项中陷入了死胡同。因此，我们要走另一条路。在下一次迭代中，我们已经有 4 个选项。 
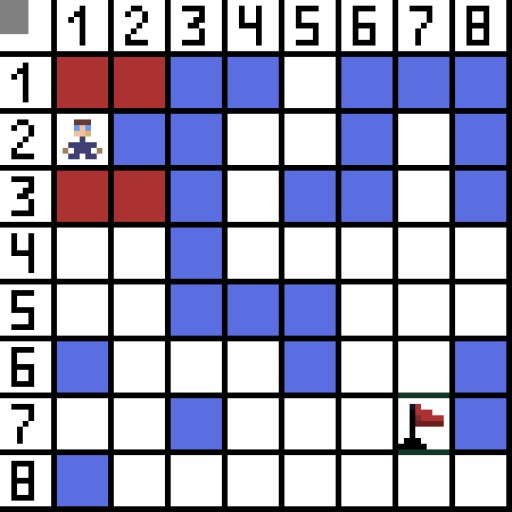其中两个不合适，因为它们向后引导，其他选项同样好，但算法决定最好沿对角线到达单元格 (3,2)。此外，在每个步骤中，重复计算函数 F，直到角色到达目标单元格。当然，如果这样的一段存在的话。 
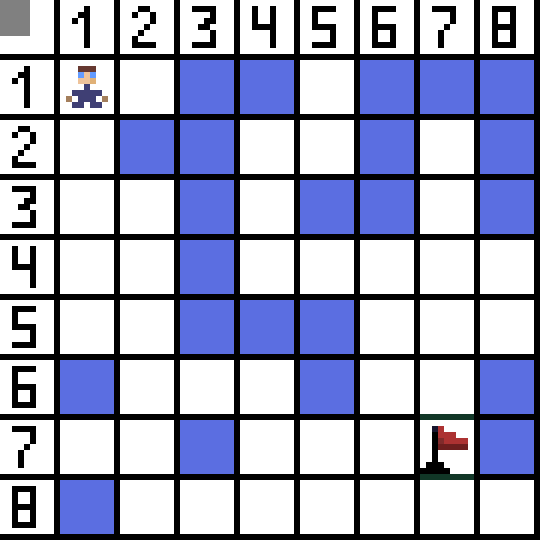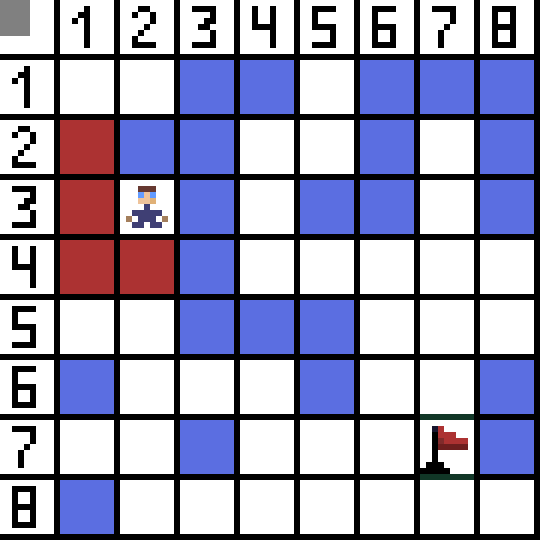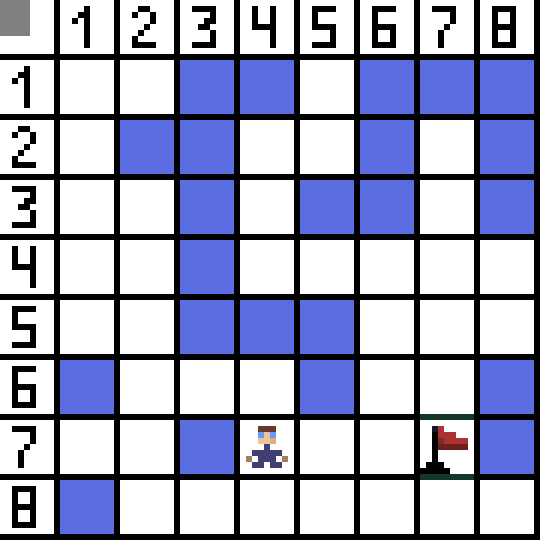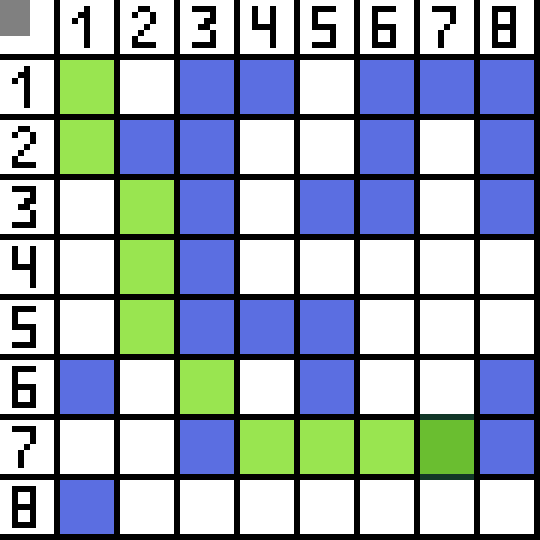gif 图片上的绿色路径表示角色到旗帜的最佳路径。
A*算法一步一步
要在 Java 中实现该算法，需要执行以下步骤 1. 首先，您需要创建两个列表，分别为开放节点和封闭节点。2. 初始化两个列表。在封闭链表中，起始节点指向开放链表。3. 当打开列表中有元素时： 3a。找到具有最小 F 3b 的节点 min。从打开列表 3c 中删除 min。确定邻居最小值（如果考虑对角线，则最多 8 个）3d。检查每个邻居：a)如果邻居是目标小区，则停止搜索b)如果不是，则为其计算G、H。G = min.G + 邻居与 min 之间的距离 F = G + H c) 如果与邻居位置相同的节点在开放列表中并且其 F 小于邻居的 F，则跳过该邻居 d) 如果与邻居位置相同的节点在关闭列表中，并且其f小于邻居的f，跳过该邻居。否则，将该节点添加到打开列表中 内循环 3e 结束。将 min 添加到闭合列表 外循环结束 因此，在每次迭代中，我们将执行下一步：- 从我们的开放列表中选择估计总分最低的单元格。
- 从打开列表中删除该单元格。
- 将我们可以到达的所有单元格添加到打开列表中。
- 当我们这样做时，我们还会处理从该节点到每个新节点的新分数，看看它是否比我们迄今为止所拥有的有所改进，如果是，我们会更新我们对该单元的了解。
A* 伪代码
下面是 A* 寻路的简短伪代码：Input: a grid with locked and empty cells, with start and goal cell.
Output: least cost path from start to goal cell.
Initialisation
openList = {startCell} //list of traversed cells
closedList = {} //list of already traversed cells
g.startCell = 0 //cost from source cell to a cell
h.startCell = h(startCell, goal) //heuristic
f.startCell = g.startCell + h.StartCell
while openList is not empty
do
//let the currentCell equal the cell with the least f value
currentCell = Cell on top of openList, with least f
if currentCell == end return
remove currentCell from openList
add currentCell to closedList
foreach n in child.currentCell
if n in closedList
continue
cost = g.currentCell + distance(currentCell,n)
if (n in openList and cost < g.n)
remove n from closedList
g.n = cost
h.n = h(n, goal)
f.n = g.n + h.n从伪代码到 Java 中的 A* 实现
A*寻路在Java实现中应该有一些方法来服务算法：- Cell，保存必要参数的结构
- 开放列表和封闭列表
- 启发式函数的计算方法
- 追踪从源到目的地的路径的方法
- 检查给定单元格是否被阻止、是否已到达、是否有效等的方法
package Asterist;
import java.util.PriorityQueue;
import java.util.Stack;
public class AAsterisk {
//Java Program to implement A* Search Algorithm
//Here we're creating a shortcut for (int, int) pair
public static class Pair {
int first;
int second;
public Pair(int first, int second){
this.first = first;
this.second = second;
}
@Override
public boolean equals(Object obj) {
return obj instanceof Pair && this.first == ((Pair)obj).first && this.second == ((Pair)obj).second;
}
}
// Creating a shortcut for tuple<int, int, int> type
public static class Details {
double value;
int i;
int j;
public Details(double value, int i, int j) {
this.value = value;
this.i = i;
this.j = j;
}
}
// a Cell (node) structure
public static class Cell {
public Pair parent;
// f = g + h, where h is heuristic
public double f, g, h;
Cell()
{
parent = new Pair(-1, -1);
f = -1;
g = -1;
h = -1;
}
public Cell(Pair parent, double f, double g, double h) {
this.parent = parent;
this.f = f;
this.g = g;
this.h = h;
}
}
// method to check if our cell (row, col) is valid
boolean isValid(int[][] grid, int rows, int cols,
Pair point)
{
if (rows > 0 && cols > 0)
return (point.first >= 0) && (point.first < rows)
&& (point.second >= 0)
&& (point.second < cols);
return false;
}
//is the cell blocked?
boolean isUnBlocked(int[][] grid, int rows, int cols,
Pair point)
{
return isValid(grid, rows, cols, point)
&& grid[point.first][point.second] == 1;
}
//Method to check if destination cell has been already reached
boolean isDestination(Pair position, Pair dest)
{
return position == dest || position.equals(dest);
}
// Method to calculate heuristic function
double calculateHValue(Pair src, Pair dest)
{
return Math.sqrt(Math.pow((src.first - dest.first), 2.0) + Math.pow((src.second - dest.second), 2.0));
}
// Method for tracking the path from source to destination
void tracePath(
Cell[][] cellDetails,
int cols,
int rows,
Pair dest)
{ //A* Search algorithm path
System.out.println("The Path: ");
Stack<Pair> path = new Stack<>();
int row = dest.first;
int col = dest.second;
Pair nextNode = cellDetails[row][col].parent;
do {
path.push(new Pair(row, col));
nextNode = cellDetails[row][col].parent;
row = nextNode.first;
col = nextNode.second;
} while (cellDetails[row][col].parent != nextNode); // until src
while (!path.empty()) {
Pair p = path.peek();
path.pop();
System.out.println("-> (" + p.first + "," + p.second + ") ");
}
}
// A main method, A* Search algorithm to find the shortest path
void aStarSearch(int[][] grid,
int rows,
int cols,
Pair src,
Pair dest)
{
if (!isValid(grid, rows, cols, src)) {
System.out.println("Source is invalid...");
return;
}
if (!isValid(grid, rows, cols, dest)) {
System.out.println("Destination is invalid...");
return;
}
if (!isUnBlocked(grid, rows, cols, src)
|| !isUnBlocked(grid, rows, cols, dest)) {
System.out.println("Source or destination is blocked...");
return;
}
if (isDestination(src, dest)) {
System.out.println("We're already (t)here...");
return;
}
boolean[][] closedList = new boolean[rows][cols];//our closed list
Cell[][] cellDetails = new Cell[rows][cols];
int i, j;
// Initialising of the starting cell
i = src.first;
j = src.second;
cellDetails[i][j] = new Cell();
cellDetails[i][j].f = 0.0;
cellDetails[i][j].g = 0.0;
cellDetails[i][j].h = 0.0;
cellDetails[i][j].parent = new Pair( i, j );
// Creating an open list
PriorityQueue<Details> openList = new PriorityQueue<>((o1, o2) -> (int) Math.round(o1.value - o2.value));
// Put the starting cell on the open list, set f.startCell = 0
openList.add(new Details(0.0, i, j));
while (!openList.isEmpty()) {
Details p = openList.peek();
// Add to the closed list
i = p.i; // second element of tuple
j = p.j; // third element of tuple
// Remove from the open list
openList.poll();
closedList[i][j] = true;
// Generating all the 8 neighbors of the cell
for (int addX = -1; addX <= 1; addX++) {
for (int addY = -1; addY <= 1; addY++) {
Pair neighbour = new Pair(i + addX, j + addY);
if (isValid(grid, rows, cols, neighbour)) {
if(cellDetails[neighbour.first] == null){ cellDetails[neighbour.first] = new Cell[cols]; }
if (cellDetails[neighbour.first][neighbour.second] == null) {
cellDetails[neighbour.first][neighbour.second] = new Cell();
}
if (isDestination(neighbour, dest)) {
cellDetails[neighbour.first][neighbour.second].parent = new Pair ( i, j );
System.out.println("The destination cell is found");
tracePath(cellDetails, rows, cols, dest);
return;
}
else if (!closedList[neighbour.first][neighbour.second]
&& isUnBlocked(grid, rows, cols, neighbour)) {
double gNew, hNew, fNew;
gNew = cellDetails[i][j].g + 1.0;
hNew = calculateHValue(neighbour, dest);
fNew = gNew + hNew;
if (cellDetails[neighbour.first][neighbour.second].f == -1
|| cellDetails[neighbour.first][neighbour.second].f > fNew) {
openList.add(new Details(fNew, neighbour.first, neighbour.second));
// Update the details of this
// cell
cellDetails[neighbour.first][neighbour.second].g = gNew;
//heuristic function cellDetails[neighbour.first][neighbour.second].h = hNew;
cellDetails[neighbour.first][neighbour.second].f = fNew;
cellDetails[neighbour.first][neighbour.second].parent = new Pair( i, j );
}
}
}
}
}
}
System.out.println("Failed to find the Destination Cell");
}
// test
public static void main(String[] args) {
//0: The cell is blocked
// 1: The cell is not blocked
int[][] grid = {
{ 1, 1, 0, 0, 1, 0, 0, 0 },
{ 1, 0, 0, 1, 1, 0, 1, 0 },
{ 1, 1, 0, 1, 0, 0, 1, 0 },
{ 1, 1, 0, 1, 1, 1, 1, 1 },
{ 1, 1, 0, 0, 0, 1, 1, 1 },
{ 0, 1, 1, 1, 0, 1, 1, 0 },
{ 1, 1, 0, 1, 1, 1, 1, 0 },
{ 0, 1, 1, 1, 1, 1, 1, 1 }
};
// Start is the left-most upper-most corner
Pair src = new Pair(0,0);
//(8, 0);
// Destination is the right-most bottom-most corner
Pair dest = new Pair(6, 6);
AAsterisk app = new AAsterisk();
app.aStarSearch(grid, grid.length , grid[0].length, src, dest);
}
}
路径： -> (0,0) -> (1,0) -> (2,1) -> (3,1) -> (4,1) -> (5,2) -> (5, 3) -> (6,4) -> (6,5) -> (6,6)
可以看出，这是这两点之间可以建立的几条最短路径之一。请注意，图片示例中的第六步和程序输出中的第六步是不同的，尽管这些路径同样有效。该程序选择众多最有效的选项之一。
GO TO FULL VERSION