さまざまな検索アルゴリズムがさまざまなタスクに合わせて調整されています。今日は、最も効果的な経路探索アルゴリズムの 1 つである A* 探索について説明します。これは、コンピュータ ゲームや都市間の道などの検索グラフの作成に非常に適しています。たとえば、戦略的または戦術的なビデオ ゲームで、プレイヤーまたはグループがボタンを押した後、遅滞なく直ちに開始してフィールドを横切って指定した地点に移動することに気づいたかもしれません。ゲームでは、プレーヤーがどこに行く必要があるかを正確に計算する効果的なアルゴリズムが使用されているため、遅延はありません。あるいは、間違いなくプレイヤーを見つけて、遠くから正しい方向に歩き始める敵。通常、このようなアクションには A* アルゴリズムが使用されます。
A*アルゴリズムとは
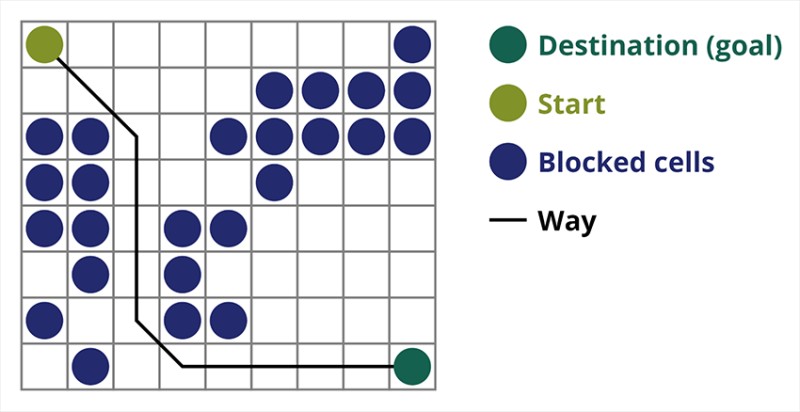
経路探索アルゴリズム A* は、最良優先探索アルゴリズムの一例です。A* アルゴリズムの目的は、ある点から別の点へのパスを見つけることです。これは、グラフ検索アルゴリズムの古典的な 1 つです。例を使用してそれがどのように機能するかを見てみましょう。トップダウンビューの 2D ゲームを想像してください。ゲーム領域を正方形の欲張り、たとえばチェス盤のような 8*8 セルに分割しましょう。私たちのセルは、通過可能または通過不可能 (障害物) の 2 つのタイプのいずれかになります。プレイヤーまたはプレイヤーに近づく敵は、一定時間ごとに 1 つのセルを移動します。ゲームでは、通過可能なセルは、平坦な道路、草、砂など、さまざまな性質を持つことがあり、それらによってセルに沿って移動する難易度が決まりますが、話を簡単にするために、すべての通過可能なセルが同じ方法で通過すると仮定します。下の図では、青いセルが障害物です。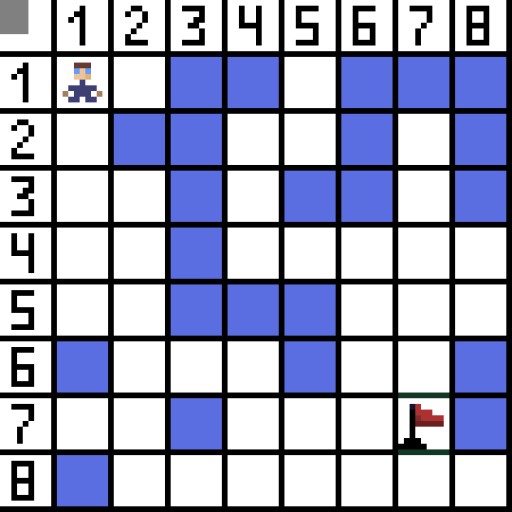
1 つのセル (またはノード) を開始セル (キャラクターがその中にある) として割り当て、もう 1 つのセルをターゲットまたはゴール セル (フラグのあるセル) として割り当て、この場合に A* アルゴリズムがどのように機能するかを説明しましょう。キャラクターはセル (1,1) にあり、ターゲットはセル (7,7) にあります。各セルには水平、垂直、斜めの隣接セルがあります。対角ノードを計算するかどうかはゲームによって異なります。たとえば、ボンバーマンやパックマンなどの多くのトップダウン ビュー ゲームでは、キャラクターは水平または垂直にしか移動できません。この場合、エッジに触れることを除いて、すべてのノードには 4 つの隣接ノードしかありません。キャラクターが斜めに移動できるゲームについて話している場合、すべてのノードは最大 8 つの隣接ノードを持つことができます。アルゴリズムの最初のステップでは、キャラクターが配置されているセルには 2 つの隣接セルがあります。正確には3つですが、そのうちの1つが障害物です。 
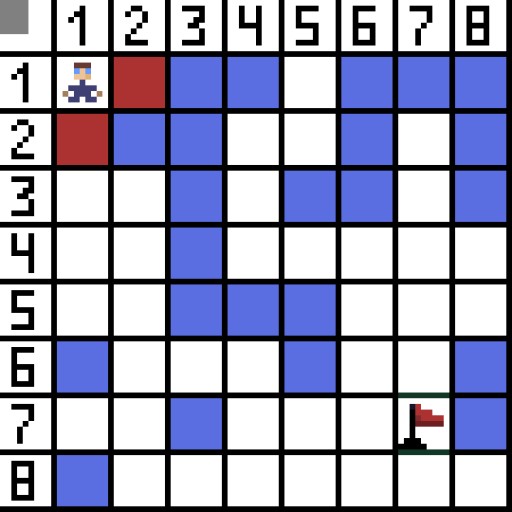明らかに斜め方向の方が長いです。セルの辺を条件付きで 1 に設定すると、このセルの対角線の長さは 2 の平方根に等しくなります。これがピタゴラスの定理の言うことです。セル A からセル B に移動するには、まず隣接するセルの 1 つを選択し、次に次のセルを選択するという手順を繰り返す必要があります。また、途中で、最初のセルからターゲットのセルに到達できるかどうかを理解します。各ステップの A* アルゴリズムは、関数 F の値に従って隣接セルの 1 つを選択します。この関数は、候補セルが最短パスにどの程度含まれるかを測定します。これはコスト関数であり、移動関数 G とヒューリスティック関数の合計です。
-
G コスト — 開始ノードからの距離です。
-
H コスト (ヒューリスティック) は、終了 (ゴール) ノードからの距離です。この関数は異なる場合があり、どちらが優れているかは開発者が決定します。おそらく A* では H の選択が最も重要であり、これがアルゴリズムの特定の実装を多かれ少なかれ効果的にするポイントです。理論的には、必要な関数を使用できます。
私たちの場合、ターゲット セルの位置がわかっているので、たとえば、ターゲットと現在のセルの間の幾何学的なユークリッド距離を計算できます。距離が短ければ短いほど、ゴールに近づきます。
-
F コスト = G + H。したがって、アルゴリズムはすべての隣接ノードの F コストを計算し、最初に調べる最も低い F コストの 1 つを選択します。1 つを選択すると、それを閉じたものとしてマークし、このノードの近傍の値を計算します。
ヒューリスティック関数 H はどのように計算できますか?
これはヒューリスティック関数です。名前自体は経験によって決定されることを意味しており、異なる場合があります。ここでは、点 (x1, y1) と (x2, y2) の間のいわゆるユークリッド距離に等しいとします。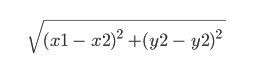
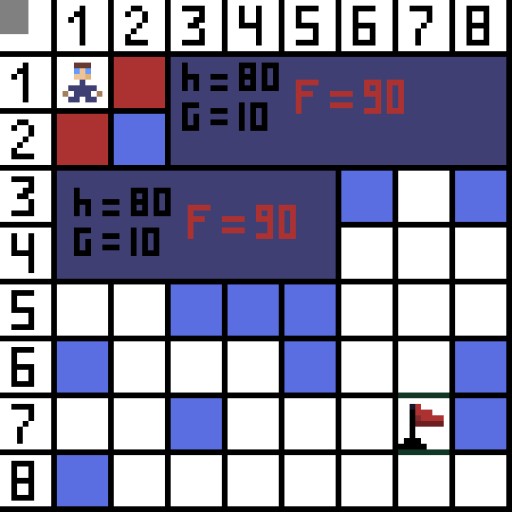図では、最初のステップには 2 つのオプションがあり、コストは同じです。しかし次のステップで、キャラクターは選択肢の 1 つで行き止まりに陥ります。したがって、私たちは別の道を進みます。次の反復では、すでに 4 つのオプションがあります。 
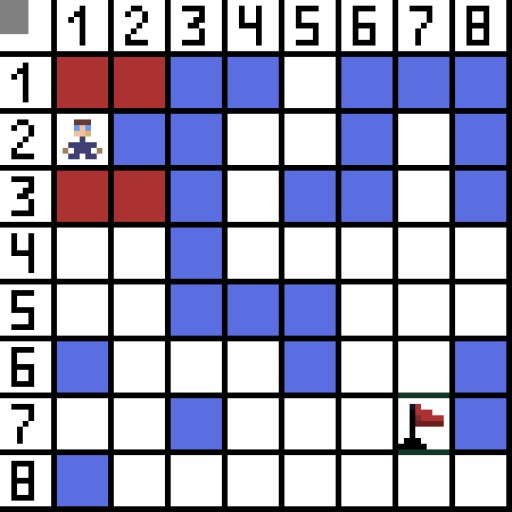そのうちの 2 つは後方に向かうため適切ではありませんが、他のオプションも同様に優れていますが、アルゴリズムはセル (3,2) に斜めに進むのが最善であると判断しました。また、各ステップにおいて、文字が対象セルに到達するまで関数Ｆの計算が繰り返される。もちろん、そのような通路が存在する場合。 
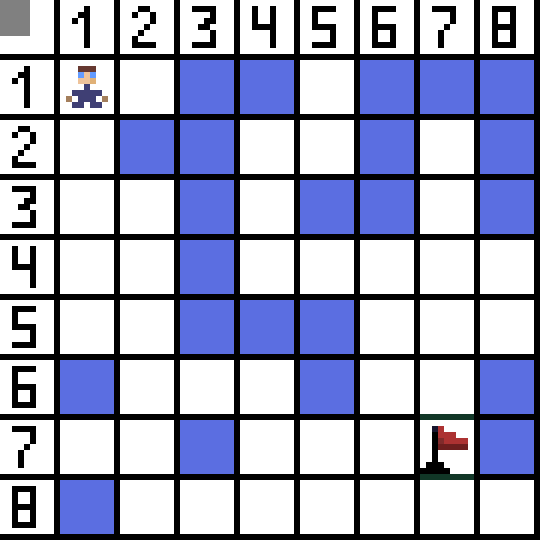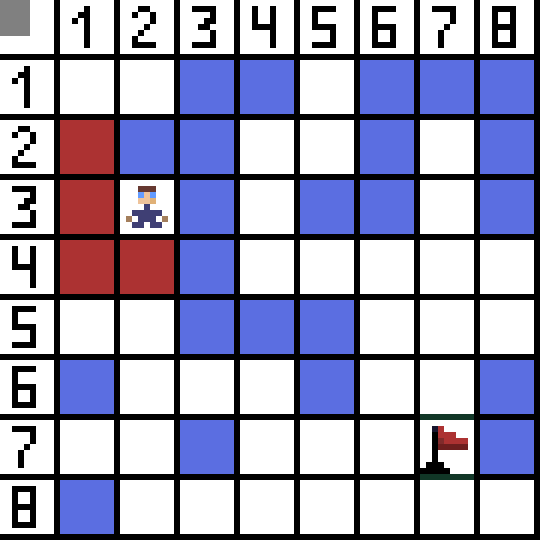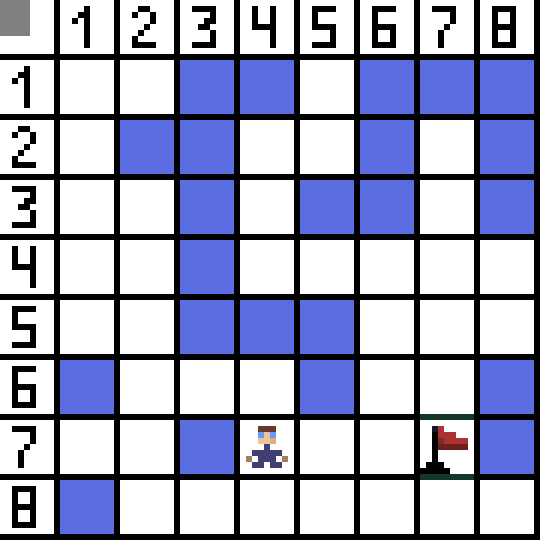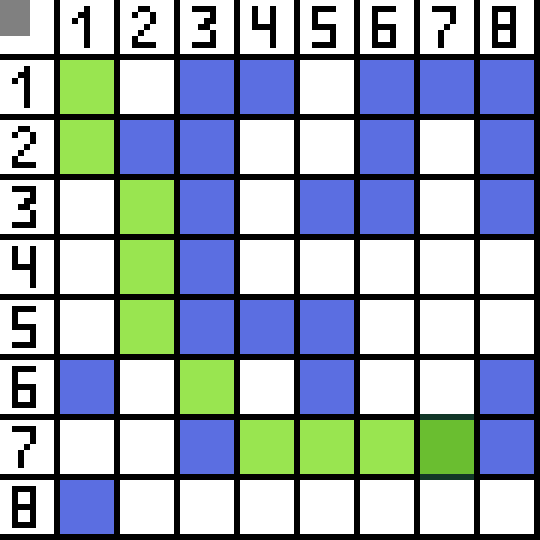GIF 画像上の緑色の方向は、キャラクターがフラグまで進む最適なパスを示しています。
A* アルゴリズムのステップバイステップ
Java でアルゴリズムを実装するには、次の手順を実行する必要があります。 1. まず、オープン ノードとクローズド ノードの 2 つのリストを作成する必要があります。2. 両方のリストを初期化します。閉じたリストでは、開始ノードは開いたリストを指します。3. 開いているリストに要素がある場合: 3a. 最小の F 3b を持つノード min を見つけます。オープンリスト 3c から min を削除します。3 次元で最小の近傍を決定します (対角線が考慮される場合は最大 8)。各隣接セルをチェックする: a) 隣接セルがターゲット セルである場合は、検索を停止します。 b) そうでない場合は、そのセルの G、H を計算します。G = min.G + 隣接ノードと最小 F の間の距離 = G + H c) 隣接ノードと同じ位置を持つノードがオープン リストにあり、その F が隣接ノードの F より小さい場合、その隣接ノードをスキップします。 d) 次の場合隣接ノードと同じ位置を持つノードが閉じたリスト内にあり、その f が隣接ノードの f より小さい場合、その隣接ノードをスキップします。それ以外の場合は、内部ループの終了リスト 3e にノードを追加します。閉じたリストに min を追加する 外側のループの終わり したがって、各反復で次のことを実行します。- 開いたリストから推定合計スコアが最も低いセルを選択します。
- このセルを開いているリストから削除します。
- そこから到達できるすべてのセルを開いているリストに追加します。
- これを行うとき、そのノードから新しいスコアをそれぞれの新しいノードに処理して、これまでのスコアが改善されているかどうかを確認し、改善されている場合は、そのセルについてわかっていることを更新します。
A* 疑似コード
A* パスファインディングの簡単な疑似コードを次に示します。Input: a grid with locked and empty cells, with start and goal cell.
Output: least cost path from start to goal cell.
Initialisation
openList = {startCell} //list of traversed cells
closedList = {} //list of already traversed cells
g.startCell = 0 //cost from source cell to a cell
h.startCell = h(startCell, goal) //heuristic
f.startCell = g.startCell + h.StartCell
while openList is not empty
do
//let the currentCell equal the cell with the least f value
currentCell = Cell on top of openList, with least f
if currentCell == end return
remove currentCell from openList
add currentCell to closedList
foreach n in child.currentCell
if n in closedList
continue
cost = g.currentCell + distance(currentCell,n)
if (n in openList and cost < g.n)
remove n from closedList
g.n = cost
h.n = h(n, goal)
f.n = g.n + h.n擬似コードから Java での A* 実装まで
A* Java でのパスファインディングの実現には、アルゴリズムを提供するいくつかのメソッドが必要です。- セル、必要なパラメータを保持する構造体
- オープンリストとクローズドリスト
- ヒューリスティック関数の計算方法
- 送信元から宛先までのパスを追跡する方法
- 指定されたセルがブロックされているかどうか、すでに到達しているかどうか、有効かどうかなどを確認するメソッド
package Asterist;
import java.util.PriorityQueue;
import java.util.Stack;
public class AAsterisk {
//Java Program to implement A* Search Algorithm
//Here we're creating a shortcut for (int, int) pair
public static class Pair {
int first;
int second;
public Pair(int first, int second){
this.first = first;
this.second = second;
}
@Override
public boolean equals(Object obj) {
return obj instanceof Pair && this.first == ((Pair)obj).first && this.second == ((Pair)obj).second;
}
}
// Creating a shortcut for tuple<int, int, int> type
public static class Details {
double value;
int i;
int j;
public Details(double value, int i, int j) {
this.value = value;
this.i = i;
this.j = j;
}
}
// a Cell (node) structure
public static class Cell {
public Pair parent;
// f = g + h, where h is heuristic
public double f, g, h;
Cell()
{
parent = new Pair(-1, -1);
f = -1;
g = -1;
h = -1;
}
public Cell(Pair parent, double f, double g, double h) {
this.parent = parent;
this.f = f;
this.g = g;
this.h = h;
}
}
// method to check if our cell (row, col) is valid
boolean isValid(int[][] grid, int rows, int cols,
Pair point)
{
if (rows > 0 && cols > 0)
return (point.first >= 0) && (point.first < rows)
&& (point.second >= 0)
&& (point.second < cols);
return false;
}
//is the cell blocked?
boolean isUnBlocked(int[][] grid, int rows, int cols,
Pair point)
{
return isValid(grid, rows, cols, point)
&& grid[point.first][point.second] == 1;
}
//Method to check if destination cell has been already reached
boolean isDestination(Pair position, Pair dest)
{
return position == dest || position.equals(dest);
}
// Method to calculate heuristic function
double calculateHValue(Pair src, Pair dest)
{
return Math.sqrt(Math.pow((src.first - dest.first), 2.0) + Math.pow((src.second - dest.second), 2.0));
}
// Method for tracking the path from source to destination
void tracePath(
Cell[][] cellDetails,
int cols,
int rows,
Pair dest)
{ //A* Search algorithm path
System.out.println("The Path: ");
Stack<Pair> path = new Stack<>();
int row = dest.first;
int col = dest.second;
Pair nextNode = cellDetails[row][col].parent;
do {
path.push(new Pair(row, col));
nextNode = cellDetails[row][col].parent;
row = nextNode.first;
col = nextNode.second;
} while (cellDetails[row][col].parent != nextNode); // until src
while (!path.empty()) {
Pair p = path.peek();
path.pop();
System.out.println("-> (" + p.first + "," + p.second + ") ");
}
}
// A main method, A* Search algorithm to find the shortest path
void aStarSearch(int[][] grid,
int rows,
int cols,
Pair src,
Pair dest)
{
if (!isValid(grid, rows, cols, src)) {
System.out.println("Source is invalid...");
return;
}
if (!isValid(grid, rows, cols, dest)) {
System.out.println("Destination is invalid...");
return;
}
if (!isUnBlocked(grid, rows, cols, src)
|| !isUnBlocked(grid, rows, cols, dest)) {
System.out.println("Source or destination is blocked...");
return;
}
if (isDestination(src, dest)) {
System.out.println("We're already (t)here...");
return;
}
boolean[][] closedList = new boolean[rows][cols];//our closed list
Cell[][] cellDetails = new Cell[rows][cols];
int i, j;
// Initialising of the starting cell
i = src.first;
j = src.second;
cellDetails[i][j] = new Cell();
cellDetails[i][j].f = 0.0;
cellDetails[i][j].g = 0.0;
cellDetails[i][j].h = 0.0;
cellDetails[i][j].parent = new Pair( i, j );
// Creating an open list
PriorityQueue<Details> openList = new PriorityQueue<>((o1, o2) -> (int) Math.round(o1.value - o2.value));
// Put the starting cell on the open list, set f.startCell = 0
openList.add(new Details(0.0, i, j));
while (!openList.isEmpty()) {
Details p = openList.peek();
// Add to the closed list
i = p.i; // second element of tuple
j = p.j; // third element of tuple
// Remove from the open list
openList.poll();
closedList[i][j] = true;
// Generating all the 8 neighbors of the cell
for (int addX = -1; addX <= 1; addX++) {
for (int addY = -1; addY <= 1; addY++) {
Pair neighbour = new Pair(i + addX, j + addY);
if (isValid(grid, rows, cols, neighbour)) {
if(cellDetails[neighbour.first] == null){ cellDetails[neighbour.first] = new Cell[cols]; }
if (cellDetails[neighbour.first][neighbour.second] == null) {
cellDetails[neighbour.first][neighbour.second] = new Cell();
}
if (isDestination(neighbour, dest)) {
cellDetails[neighbour.first][neighbour.second].parent = new Pair ( i, j );
System.out.println("The destination cell is found");
tracePath(cellDetails, rows, cols, dest);
return;
}
else if (!closedList[neighbour.first][neighbour.second]
&& isUnBlocked(grid, rows, cols, neighbour)) {
double gNew, hNew, fNew;
gNew = cellDetails[i][j].g + 1.0;
hNew = calculateHValue(neighbour, dest);
fNew = gNew + hNew;
if (cellDetails[neighbour.first][neighbour.second].f == -1
|| cellDetails[neighbour.first][neighbour.second].f > fNew) {
openList.add(new Details(fNew, neighbour.first, neighbour.second));
// Update the details of this
// cell
cellDetails[neighbour.first][neighbour.second].g = gNew;
//heuristic function cellDetails[neighbour.first][neighbour.second].h = hNew;
cellDetails[neighbour.first][neighbour.second].f = fNew;
cellDetails[neighbour.first][neighbour.second].parent = new Pair( i, j );
}
}
}
}
}
}
System.out.println("Failed to find the Destination Cell");
}
// test
public static void main(String[] args) {
//0: The cell is blocked
// 1: The cell is not blocked
int[][] grid = {
{ 1, 1, 0, 0, 1, 0, 0, 0 },
{ 1, 0, 0, 1, 1, 0, 1, 0 },
{ 1, 1, 0, 1, 0, 0, 1, 0 },
{ 1, 1, 0, 1, 1, 1, 1, 1 },
{ 1, 1, 0, 0, 0, 1, 1, 1 },
{ 0, 1, 1, 1, 0, 1, 1, 0 },
{ 1, 1, 0, 1, 1, 1, 1, 0 },
{ 0, 1, 1, 1, 1, 1, 1, 1 }
};
// Start is the left-most upper-most corner
Pair src = new Pair(0,0);
//(8, 0);
// Destination is the right-most bottom-most corner
Pair dest = new Pair(6, 6);
AAsterisk app = new AAsterisk();
app.aStarSearch(grid, grid.length , grid[0].length, src, dest);
}
}
パス: -> (0,0) -> (1,0) -> (2,1) -> (3,1) -> (4,1) -> (5,2) -> (5, 3) -> (6,4) -> (6,5) -> (6,6)
これは、これら 2 点間に構築できるいくつかの最短パスの 1 つであることがわかります。パスは同じように有効であることが判明しましたが、画像とプログラム出力の例の 6 番目のステップが異なることに注意してください。プログラムは、数多くのオプションの中から最も効果的なオプションを 1 つ選択します。
GO TO FULL VERSION